Similar presentations:
Молекулярно-кінетична теорія ідеальних газів. Основи термодинаміки
1.
Лекція 9.Молекулярно-кінетична теорія
ідеальних газів.
Основи термодинаміки.
1
2.
План лекції• Розподіл Максвелла для молекул ідеального газу за швидкостями.
• Середня арифметична, середня квадратична та найімовірніша швидкості молекул.
• Барометрична формула. Розподіл Больцмана для частинок у зовнішньому потенціальному
полі.
• Число ступенів вільності молекул.
• Робота газу при зміні його об'єму.
• Кількість теплоти.
• Перший закон термодинаміки.
• Застосування першого закону термодинаміки до ізопроцесів.
• Теплоємність. Залежність теплоємності ідеального газу від виду процесу.
• Рівняння Майєра.
• Адіабатний процес. Рівняння Пуассона.
2
3.
Розподіл Максвелла для молекул ідеального газуРозподіли Максвела для реальних
інертних газів з відчутно різними
молекулярними масами ( =4 для
гелію, та =132 для ксенону) при
кімнатній температур.
Функція Максвела має різний вигляд для молекул різної маси: чим більшою є маса
частинок, тим гостріший пік розподілу, і тим меншою є найбільш ймовірна
швидкість (визначена максимумом функції Максвела)
3
4.
Розподіл Максвелла для молекул ідеального газу зашвидкостями
dn -кількість молекул в одиниці об’єму газу,
Uz
модулі швидкостей яких знаходяться в межах
від U до U dU
dU
Ux
Uy
кінці векторів швидкостей цих молекул мають
лежати у просторі швидкостей всередині
колового шару. Об’єм цього шару
d 4 u 2 du
Під час теплового руху з причини його безладності всі
напрямки швидкостей молекул рівно вірогідні. Тому число
dn n0 f u 4 u 2 du n0 F u du
dn
F u
f u 4 u 2
n0 du
- функція розподілу Максвелла
Функція Максвелла, визначає відносну кількість молекул, яка
припадає на одиничний інтервал швидкостей
4
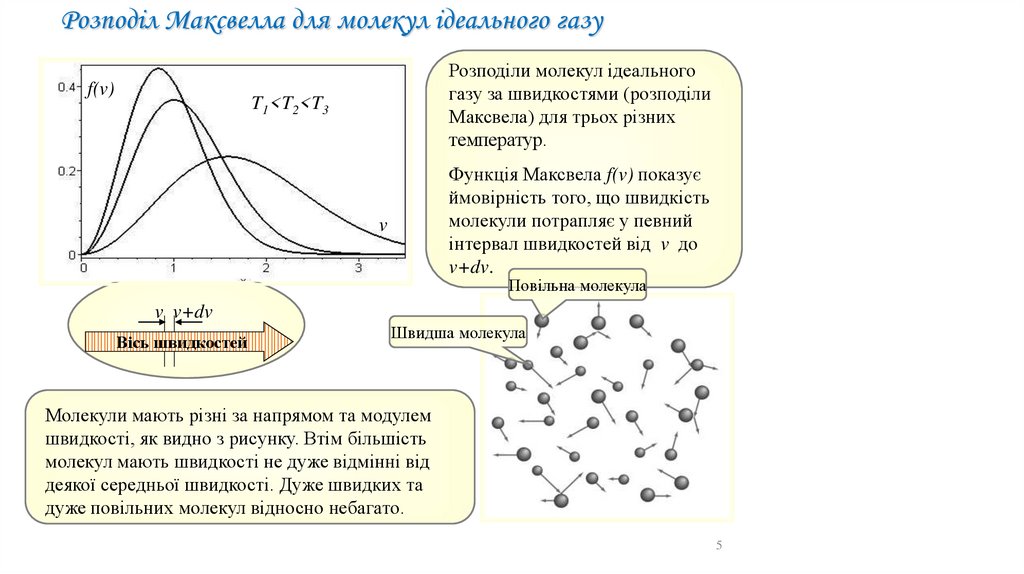
5.
Розподіл Максвелла для молекул ідеального газуf(v)
Розподіли молекул ідеального
газу за швидкостями (розподіли
Максвела) для трьох різних
температур.
T1<T2<T3
Функція Максвела f(v) показує
ймовірність того, що швидкість
молекули потрапляє у певний
інтервал швидкостей від v до
v+dv.
v
Повільна молекула
v v+dv
Вісь швидкостей
Швидша молекула
Молекули мають різні за напрямом та модулем
швидкості, як видно з рисунку. Втім більшість
молекул мають швидкості не дуже відмінні від
деякої середньої швидкості. Дуже швидких та
дуже повільних молекул відносно небагато.
5
6.
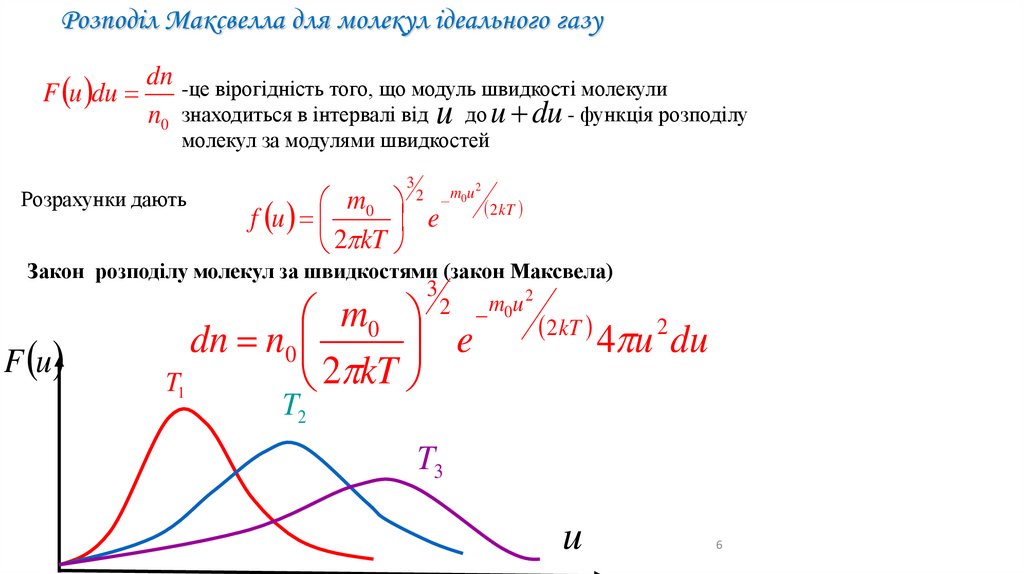
Розподіл Максвелла для молекул ідеального газуdn
F u du
n0
-це вірогідність того, що модуль швидкості молекули
знаходиться в інтервалі від
до u du - функція розподілу
молекул за модулями швидкостей
Розрахунки дають
u
3
m0
f u
e
2 kT
2
m0u 2
2 kT
Закон розподілу молекул за швидкостями (закон Максвела)
3
F u
m0
dn n0
e
2 kT
T1
2
m0u 2
2 kT
4 u du
2
T2
T3
u
6
7.
Розподіл Максвелла для молекул ідеального газуДошка Гамільтона
7
8.
Розподіл Максвелла для молекул ідеального газуi
2kT
2 RT
mo
M
1 2 ...
кв
N
8kT
8RT
mo
M
12 22 ...
N
називається найімовірнішою швидкістю
називається середньою
арифметичною швидкістю
3kT
3RT називається середньою
mo
M квадратичною швидкістю
8
9.
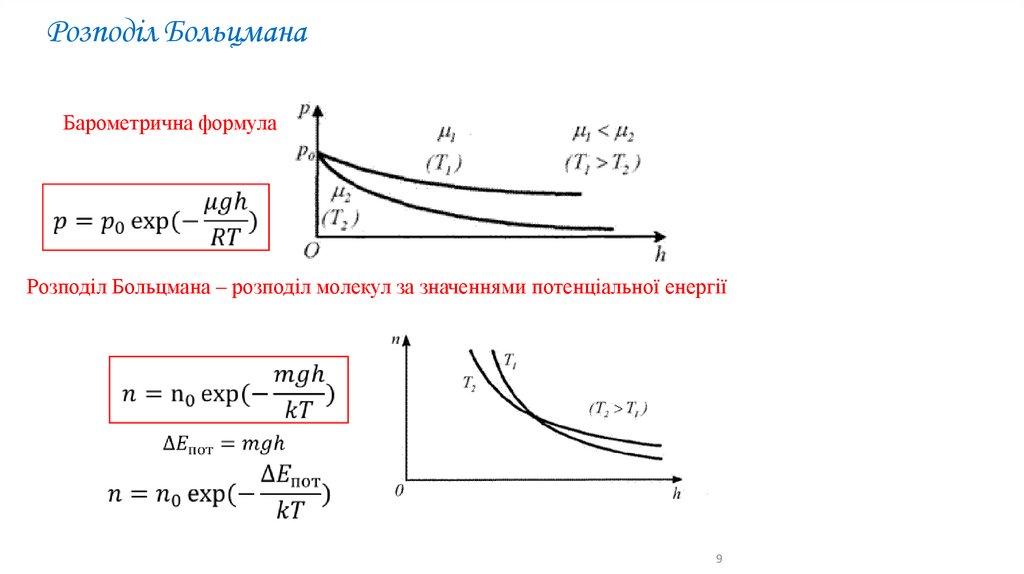
Розподіл БольцманаБарометрична формула
Розподіл Больцмана – розподіл молекул за значеннями потенціальної енергії
9
10.
yy4
y3
y2
y1
x
Ілюстрація розподілу молекул у полі сил земного
тяжіння – розподілу Больцмана.
Чим вище – тим менша концентрація молекул
10
11.
Число ступенів вільності молекулЧислом ступенів вільності тіла називається
–
найменше число незалежних координат, які необхідно задати, щоб повністю
визначити положення тіла у просторі, або кількість незалежних рухів, які може
виконувати тіло.
Наприклад, матеріальна точка, що довільно рухається у просторі, має три поступальні
ступені вільності (x, y, z). Тверде тіло має шість ступенів вільності, оскільки, воно має
три поступальні ступені вільності (x, y, z) й три обертальні – навколо осей (Оx, О y, О z).
Молекули одноатомного газу можна розглядати як матеріальні точки. Така молекула має
три
ступені
вільності
поступального
руху.
Модель
двохатомної молекули у першому наближенні – це два жорстко зв’язаних атоми, що
розташовані на деякій відстані один від одного. Вона має три ступені вільності
поступального руху і дві ступені вільності обертального руху (навколо двох осей Oy і
Oz). Трьохатомна і багатоатомна молекула має 6 ступенів вільності – 3 поступальних і 3
обертальних.
11
12.
Число ступенів вільності молекулМолекула
Модель
одноатомна
двохатомна
багатоатомна
поступальних
3
3
3
обертальних
-
2
3
усього
3
5
6
молекули
Число
ступенів вільності
За допомогою статистичного методу Больцман вивів закон рівномірного
розподілу енергії за ступенями вільності молекул: у стані термодинамічної
рівноваги на кожний поступальний і обертальний ступінь вільності молекули
у середньому припадає кінетична енергія, що дорівнює < 1> = 1 kT
2
.
Таким чином середня кінетична енергія молекули визначається за формулою:
i
o kT
2
де і – число ступенів вільності молекули, і = іпост + іоберт.
12
13.
ТермодинамікаТермодинаміка вивчає:
закони взаємних перетворень різних видів енергії, та їх залежність від різних
факторів.
переходи енергії з однієї форми в іншу, від однієї частини системи – до іншої;
енергетичні ефекти, що супроводжують різноманітні хімічні і фізичні процеси, їх
залежність від умов протікання процесу;
можливість, напрямок і межі протікання самочинних (без затрат енергії) процесів
за заданих умов.
Термодинамічна система - сукупність тіл, що взаємодіють між собою, і
відмежовані від оточуючого середовища реальною або уявною оболонкою.
Види систем
Відкриті – обмін і масою і енергією
Закриті – обмін тільки енергією
Ізольовані - немає обміну
13
14.
Внутрішня енергія, робота, теплотаТермодинамічна система (ТДС) – це фізична система, що складається з великої кількості
мікрочастинок, які беруть участь у тепловому русі, взаємодіють між собою та з навколишнім
середовищем, обмінюючись, зокрема, енергією.
Термодинамічний процес – це процес переходу системи .з одного початкового стану в інший через
послідовність проміжних станів.
Важливою характеристикою стану термодинамічної системи є її
внутрішня енергія U – це кінетична енергія хаотичного теплового руху мікрочастинок (молекул,
атомів тощо) і потенціальна енергія їх взаємодії.
Внутрішня енергія – однозначна функція стану термодинамічної системи, тобто у кожному стані,
який характеризується параметрами P, V, T, система має цілком визначене значення внутрішньої
енергії U. Початком відліку внутрішньої енергії звичайно вважають стан при T = 0 К. Хоча при
переході з одного стану в інший практичний інтерес має тільки зміна внутрішньої енергії U, тому
вибір початку відліку не має особливого значення.
В ідеальному газі не враховуються сили взаємодії між молекулами, а отже, потенціальна енергія
молекул дорівнює нулю. Тому внутрішня енергія ідеального газу дорівнює сумарній кінетичній
енергії їх теплового руху:
i
i
i m
U = < o>N = kT N A
RT RT
2
2M
2
Внутрішня енергія ідеального газу залежить від виду газу (кількості ступенів вільності молекул) і
його абсолютної температури.
14
15.
Внутрішня енергія, робота, теплотаОбмін енергією ТДС із зовнішнім середовищем може відбуватися двома способами: при силовій
взаємодії (шляхом виконання роботи) або шляхом теплообміну.
Робота – це форма передавання енергії при силовій взаємодії.
Друга форма передавання енергії здійснюється при безпосередньому обміні енергіями між
молекулами взаємодіючих тіл, тобто у процесі теплообміну. Таку форму передавання енергії у
термодинаміці називають теплотою.
Теплообмін відбувається у випадку різниці температури взаємодіючих тіл. Унаслідок теплообміну
температури тіл вирівнюються.
Робота і теплота мають ту спільну властивість, що вони є характеристикою процесу передавання
енергії, а їх числові значення істотно залежать від виду процесу. Проте між роботою і теплотою існує
глибока якісна відмінність. Виконання роботи над системою може змінити будь-який вид її енергії –
механічної (кінетичної та потенціальної) або внутрішньої. Теплота може змінити тільки внутрішню
енергію системи.
15
16.
Способи змінивнутрішньої енергії
Теплообмін
(теплопередача)
конвекція
випромінювання
Виконання
роботи
теплопровідність
•теплопровідність:
передача внутрішньої
енергії від більш
нагрітих ділянок тіла до
менш нагрітих за
рахунок співударянь
молекул речовини;
•конвекція:
перемішування теплих
та холодних шарів
рідини або газу за
рахунок різниці їх
густин;
•випромінювання:
передача енергії за
допомогою
електромагнітних
хвиль (світла, зокрема).
16
17.
F pSdA Fdl pSdl pdV
dA pdV
dl
p
l1
l2
Робота у загальному випадку:
A
V2
pdV
V1
17
18.
Ap const
V const
pdV p V
2
V1
V1
A
T const
V2
V2
V1
V2
V2
m
dV m
pdV
RT
RT ln
M
V
M
V1
V1
A
V2
pdV 0
V1
18
19.
З рисунку видно, що різні способи переходу від стану 1 достану 2, характеризуються різною роботою, здійсненою
системою.
19
20.
Кількість теплоти - це енергія, яка передається тілу впроцесі теплопередачі ззовні.
Теплопередача – це такий процес, при якому внутрішня
енергія одних тіл зменшується, а інших – відповідно
збільшується, причому механічна енергія тіл не змінюється і
робота не виконується.
Кількість теплоти, яку потрібно надати будь-якому тілу,
щоб підвищити його температуру на 1 К, називається
теплоємністю цього тіла.
dQ
C
dT
Дж
[C ]
.
К
20
21.
Питома теплоємність - це фізична величина, що показує,яку кількість теплоти потрібно затратити, щоб нагріти
одиницю маси речовини на один Кельвін:
dQ
c
m dT
Дж
[с ]
.
кг К
Кількість теплоти, яку потрібно надати одному молю
речовини, щоб підвищити його температуру на один
Кельвін називається молярною теплоємністю
CM
dQ
dT
Дж
[C м ]
.
моль К
21
22.
.Розглянемо термодинамічну систему (газ), яка переходить із одного стану, що
характеризується параметрами (P1,V1,T1), в інший (P2,V2,T2): (1) (2). Проаналізуємо
цей перехід з енергетичної точки зору. У першому стані внутрішня енергія
дорівнювала U1, у другому – U2. Зміна внутрішньої енергії дорівнює U12 =U2 – U1.
Внутрішню енергію можна змінити двома способами: шляхом виконання роботи
зовнішніми тілами над системою (газом) та шляхом теплопередавання, тобто
надання теплоти від зовнішніх тіл до системи:
U12=A12зовн Q12
Урахувавши, що робота, яка виконується газом проти зовнішніх сил, дорівнює
роботі, що виконується зовнішніми силами, з протилежним знаком, отримаємо:
Q12 U12 A12
Це рівняння – математичний вираз першого закону термодинаміки: теплота, яка
передається системі (газу), витрачається на збільшення її внутрішньої енергії та
на виконання системою роботи проти зовнішніх сил.
Перший закон термодинаміки є наслідком закону збереження енергії.
22
23.
iQ dU A, dQ RdT pdV
2
де dU - повний диференціал, Q та A – функціонали.
Різниця між функціоналом та повним диференціалом
полягає у тому, що dU характеризує внутрішній стан
системи і не залежить від шляху системи, а Q та A
залежать від шляху, тобто послідовності станів системи.
23
24.
idQ RdT pdV
2
i
i 2
i 2
Q R T p V
R T
p V
2
2
2
dQ
i 2
Cp
R
dT
2
24
25.
dT 0 dU 0 mdQ dA
V2
Q
RT ln
pdV
M
V1
CT
dV 0 dA 0
i
i m
dQ dU
RdT Q U R T
2
2M
i
CV
Рівняння Маєра:
2
R
C p CV R
25
26.
Адіабатним називається процес, який протікає безтеплообміну dQ 0 із зовнішнім середовищем
Рівняння Маєра:
Сp
СV
С p СV R
- показник Пуассона
Сp
R
1
СV
СV
R
1
СV
Перший закон термодинаміки:
i m
m
dQ
RdT pdV CV
dT pdV 0
2M
M
m
1
p RT
M
V
з рівняння Мендєлєєва – Клапейрона
26
27.
mm RT
RT
СV dT
dV 0 СV dT
dV 0 : TCV
M
M V
V
dT R dV
0
T CV V
ln T
або
R
ln V const
СV
R
d ln T
ln V 0
СV
ln T 1 ln V const ,
ln T ln V 1 const ln T V 1 const T V 1 const
T V 1 const - рівняння адіабати
M pV
З рівняння Менделєєва Клапейрона:
T
m R
M pV
mRconst
1
1
V
const pV V
pV const
m R
M
27
28.
pАдіабата
Ізотерма
T V
1
const
pV const
Сp
i 2
СV
i
V
- показник адіабати
Для одноатомного газу: 5 1, 67
3
7
Для двохатомного газу: 1, 4
5
8
Для трьохатомного газу: 6 1,33
Адіабата спадає крутіше
ніж
ізотерма.
Це
пояснюється тим, що при
адіабатичному стисненні
збільшення тиску газу
зумовлено
не
тільки
зменшенням його об'єму,
як
при ізотермічному
стисненні,
а
й
підвищенням температури.
28
29.
Ну, якось так…29


























 physics
physics








