Цилиндр

1.

2.

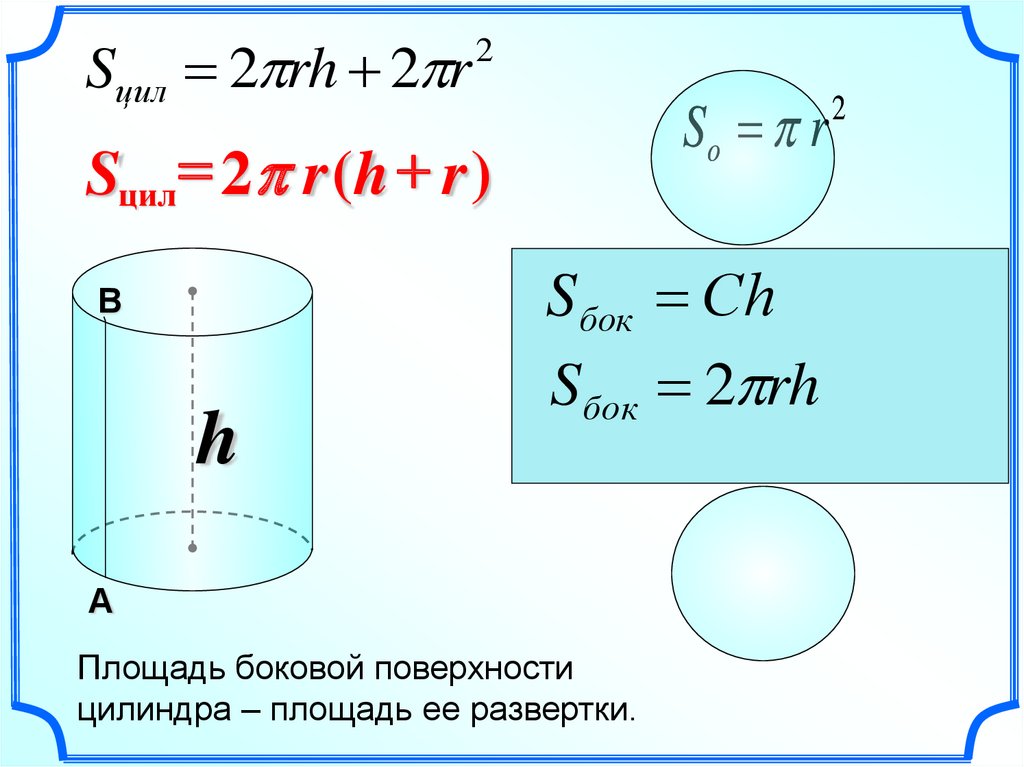
Sцил 2 rh 2 r
2
Sо r
Sцил 2 r (h r )
В
h
S бок Сh
Sбок 2 rh
А
Площадь боковой поверхности
цилиндра – площадь ее развертки.
2

3.

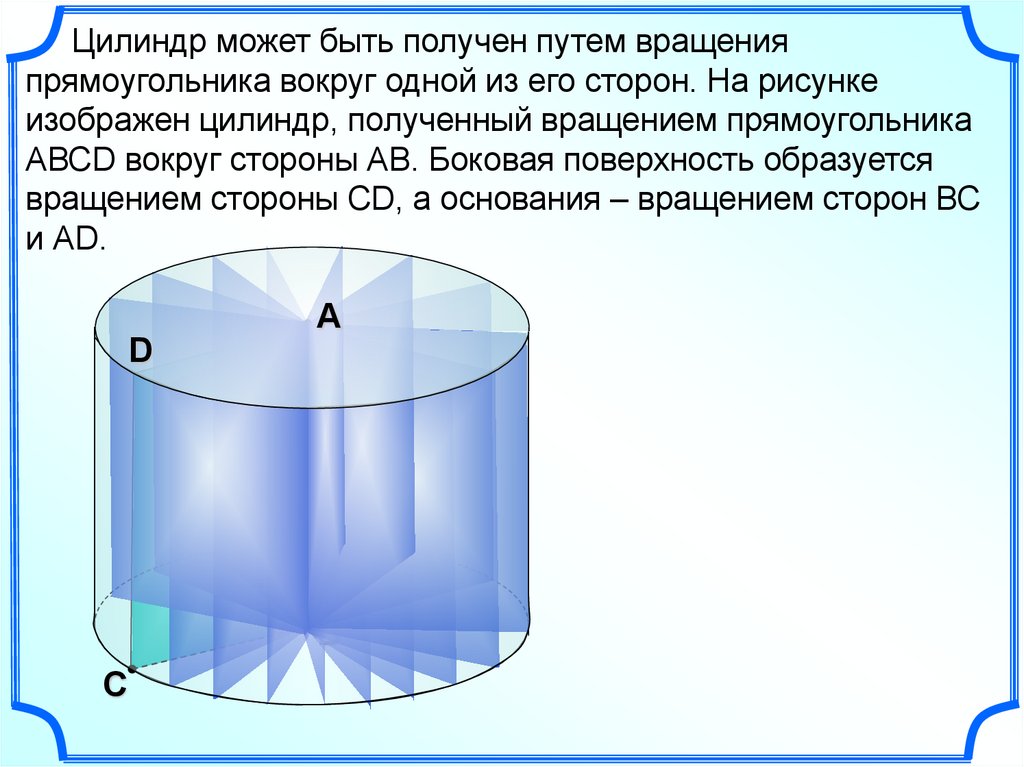
Цилиндр может быть получен путем вращения
прямоугольника вокруг одной из его сторон. На рисунке
изображен цилиндр, полученный вращением прямоугольника
АВСD вокруг стороны АВ. Боковая поверхность образуется
вращением стороны СD, а основания – вращением сторон ВС
и АD.
А
D
В
С

4.

1 вариант
Квадрат вращают вокруг одной из его сторон. Найти площадь
осевого сечения получившегося цилиндра, его боковую
поверхность и полную поверхность цилиндра, если сторона
квадрата а см, где а см – это ваш порядковый номер в списке
класса. Сколько потребуется краски, чтобы покрасить такой
цилиндр снаружи, если расход краски на 1квадратный см –
0,02г.
2 вариант
Прямоугольник вращают вокруг его ширины. Найти площадь
осевого сечения получившегося цилиндра, его боковую
поверхность и полную поверхность цилиндра, если ширина
прямоугольника 0,3м, длина а м – ваш порядковый номер в
списке класса. Сколько потребуется краски, чтобы покрасить
такой цилиндр снаружи, если расход краски на 1квадратный
метр – 200г.

5.

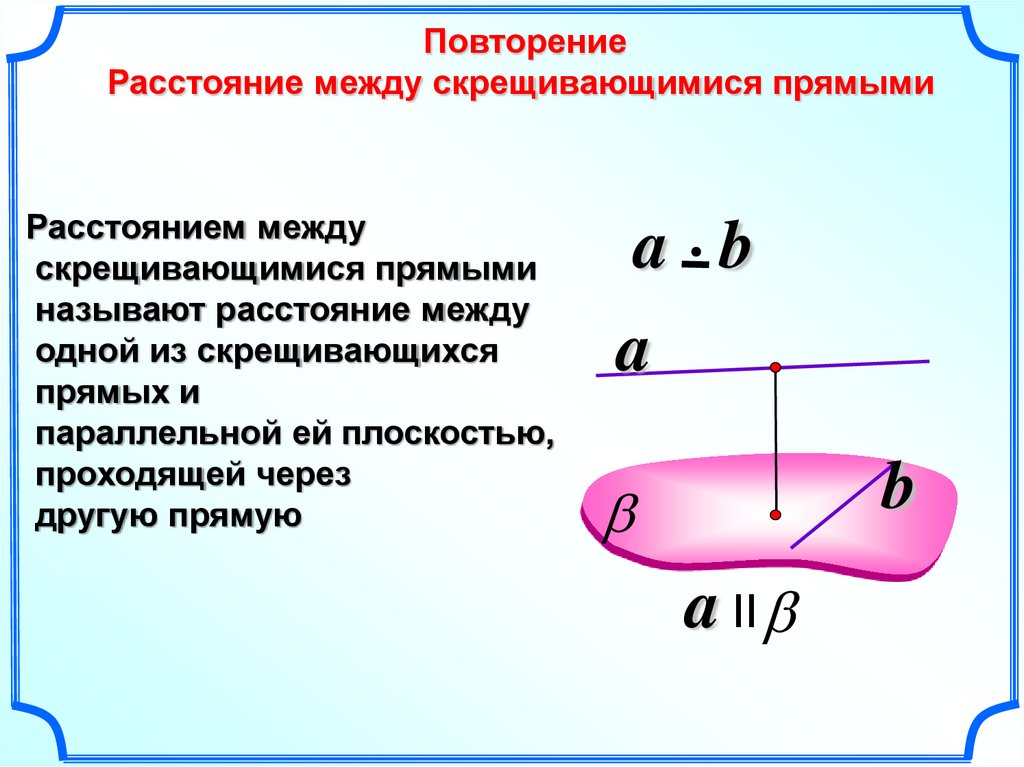
Повторение
Расстояние между скрещивающимися прямыми
Расстоянием между
скрещивающимися прямыми
называют расстояние между
одной из скрещивающихся
прямых и
параллельной ей плоскостью,
проходящей через
другую прямую
a b
a
b
a II

6.

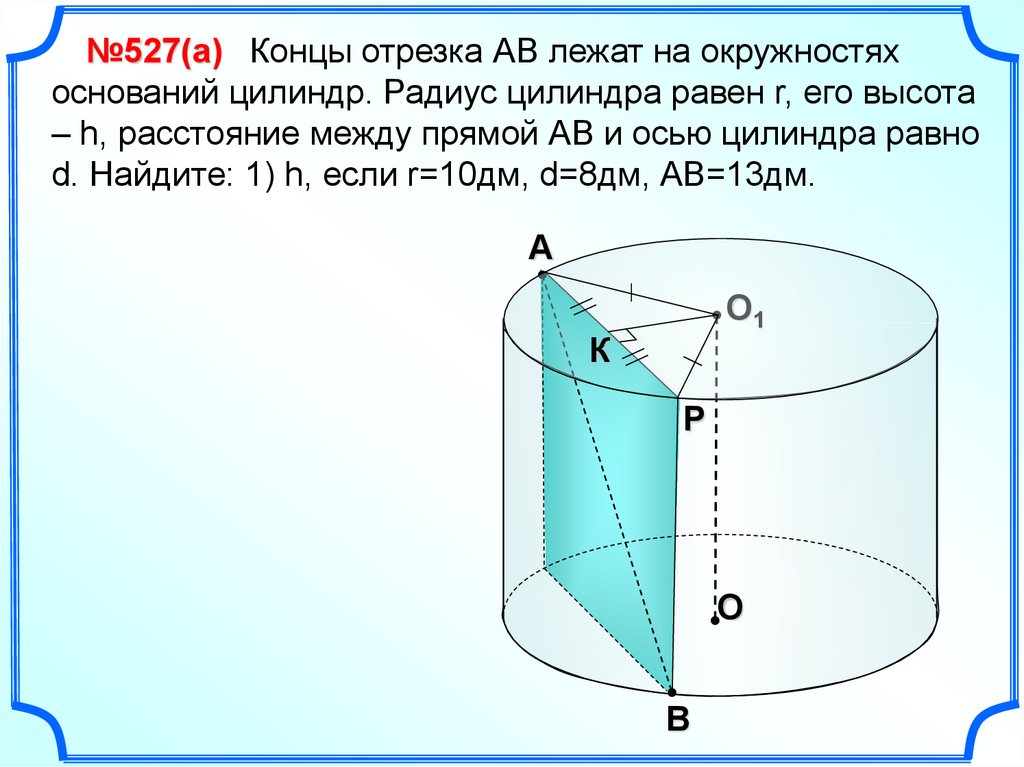
№527(а) Концы отрезка АВ лежат на окружностях
оснований цилиндр. Радиус цилиндра равен r, его высота
– h, расстояние между прямой АВ и осью цилиндра равно
d. Найдите: 1) h, если r=10дм, d=8дм, АВ=13дм.
А
O1
К
Р
O
В

7.

2. Осевое сечение цилиндра – квадрат, длина диагонали
которого 24 см. Найдите радиус основания цилиндра и
площадь боковой поверхности.
А
D
24
В
С

8.

3. ПРОФИЛЬ
Через образующую цилиндра проведено
два сечения, одно из которых осевое. Площадь меньшего из
сечений равна 40см2. Угол между плоскостями 300. Найти
площадь второго сечения.
А
300
O1
В
С
O