Основы молекулярно-кинетической теории

1. Лекция

Молекулярнокинетическая теория

2.

Макроскопические тела- тела состоящие из
большого числа молекул
1. Статистический метод – основан на том, что
св-ва макроскопической сис-мы опр-ся св-ми
частиц сис-мы и усредненными значениями
хар-к этих частиц ( скорость, энергия и пр.)
2. Термодинамический метод – основан на том,
что макроскопические тела могут
обмениваться энергией как с друг другом так и
с внешней средой ( давление, объем,
температура)

3.

Молекулярно-кинетическая теория
1. Вещество состоит из мельчайших частиц
(атомов или молекул)
2. Частицы в-ва находятся в непрерывном
хаотическом движении, скорость которого
определяет T тела
3. Между частицами существуют силы
притяжения и оттталкивания

4.

Засисимость силы
взаимодействия от расстояния
Fот
F
r > r0 – силы притяжения
r < r0 – силы отталкивания
Fпр
r = r0 силы =0

5.

Идеальный газ
1. Собственный объем молекул газа
пренебрежимо мал по сравнению с объемом
сосуда
2. Между молекулами газ отсутствуют силы
взаимодействия
3. Столкновения молекул газа между собой и
со стенками сосуда абсолютно упругие
Закон Авогадро
Закон Дальтона
Закон Бойля-Мариотта
Закон Гей-Люссака
Закон Шарля
Опытные
законы

6.

Закон Авогадро – моли любых газов при
одинаковых T и P занимают одинаковый объем
При нормальных условиях Vm=22,41•10-3 м3
Постоянная Авогадро – число молекул в
одном моле в-ва NA = 6,022•1023
Моль в-ва – кол-во в-ва, содержащее NA
структурных элементов (атомов)
Закон Дальтона - давление смеси ид. газов, равно
сумме парциальных давлений входящих в нее газов
P = P1 + P2 + P3 +…
Парциальное дав-ние – дав-ние, которое
производил бы газ, если бы один занимал весь
объем смеси при той же температуре

7.

Закон Бойля-Мариотта – для данной массы газа
при Т=const произведение давления газа на его
объем есть величина постоянная
Изотермический
процесс – процесс
при постоянной
температуре
PV = const
P1V1=P2V2
Закон Гей-Люссака – для данной массы газа при
постоянном давлении объем
изм-ся линейно с температурой
Изобарный процесс
– при постоянном
давлении
V
const
T
V V0 T

8.

Закон Шарля – давление данной массы при
постоянном давлении изм-ся линейно с Т.
Процесс
изохорный – при
постоянном объеме
Из законов
P
const
T
P P0 T
PV
b
T
b = const, массе
Уравнение состояния идеального газа ( урние Клайперона) связывает между собой
термодинамические (макроскопические)
параметры системы
b =???

9.

При нормальных условиях
PaVm 0 1,013 10 22,4 10
Tл
273,15
5
Газовая постоянная
3
Дж
8,31
R
моль К
Для произвольного объема V массой m
M – Vm
Из
пропорции
m - V
m
PV
RT RT
M
MV
Vm
m
-число молей
газа
Уравнение Менделеева-Клайперона

10.

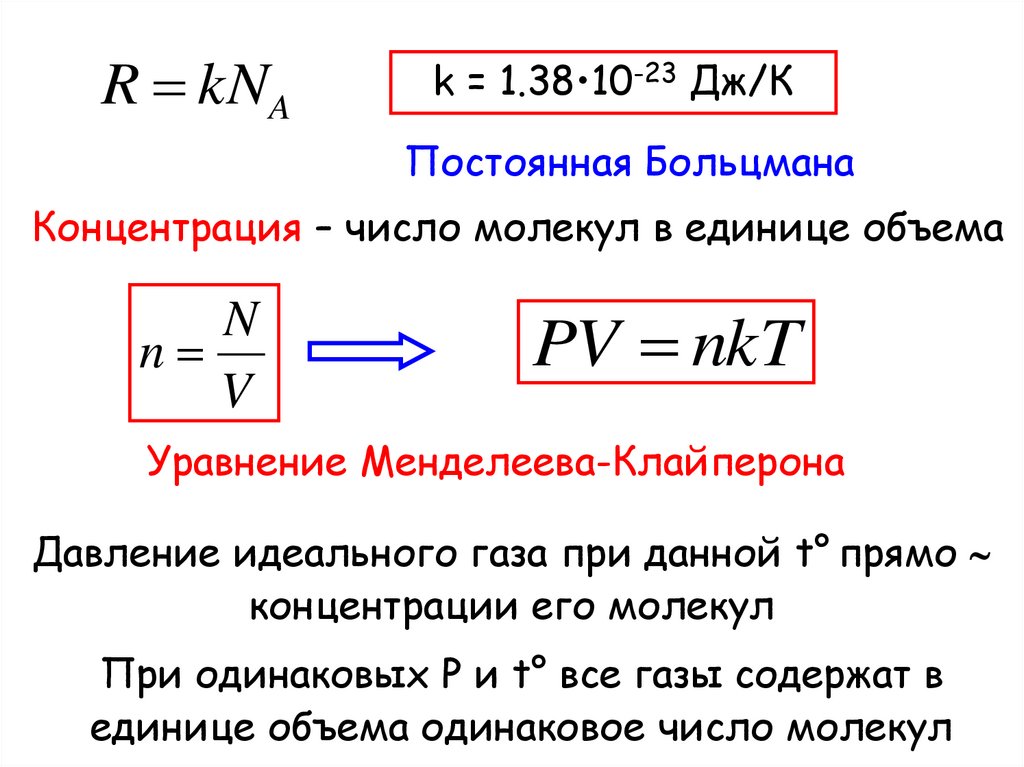
R kNA
k = 1.38•10-23 Дж/К
Постоянная Больцмана
Концентрация – число молекул в единице объема
N
n
V
PV nkT
Уравнение Менделеева-Клайперона
Давление идеального газа при данной t° прямо
концентрации его молекул
При одинаковых P и t° все газы содержат в
единице объема одинаковое число молекул

11.

p m0 ( m0 ) 2m0
t
n S t
p 2nm0 S t
2
Импульс передаваемый 1
молекулой
Число молекул в цилиндре
Импульс всех молекул
Равновероятное движение молекул по 6-ти
направлениям Х,Y,Z и –X, -Y,-Z
1
2
p nm0 S t
3
2
1
N
2
i

12.

F
p
Сила давления на стенку сосуда
Делим на площадь
t
n
2
2
P m0 n пост
3
3
пост
1
2
m0
2
Основное
уравнение МКТ
Среднее зн-ние кинет.
2
kT энергии поступ. дв-ния
3
молекул
Давление идеального газа опр-ся средним зн-нием
кинет. энергии молекул
Температура явл-ся мерой средней энергии
молекул

13.

пост
R kNA
1
2
2
m0 kT
2
3
3kТ
3RТ
υкв
m0
M
Для данного газа средняя
квад-ная скорость зависит
только от температуры
Статистическая хар-ка!!!!!
В каждом интервале будет нах-ся N молекул
с этой скоростью – распределение числа молекул
по скоростям
3
2
4 M
f (υ)
e
2kT
Mυ 2
2 kT
υ
2

14.

Функция распределения молекул по скоростям
Максвелла- опр. относительное число мол-л
скорости которых лежат в интервале от до +
2 RT
υв
M
8RТ
2,25RT
υср
M
M
Средняя арифметическая
скорость
Наиболее
вероятная
скорость
кв < ар < в

15.

При изменении тем-ры изм-ся и скорость всех
молекул газа
Кол-во молекул не
зависит от тем-ры
Площадь под кривой f(υ) =
const и будет изменяться
положение
максимума
кривой
При тем-ры мак-м , при тем-ры мак-м
Положение мак-ма зависит от природы газа.
Больше молярная масса
При тем-ры мак-м кривой растет
При одинаковой тем-ре и разной массе одного газа
- площадь под кривой больше, для большей массы

16.

( P dP) P gdh
P2 P1e
Mg ( h2 h1 )
RT
Обозначим P1 = P0 и h1=h0 ,
где P0 и h0 давление и
высота на уровне моря
P P0e
Mgh
RT
барометрическая
формула
P убывает с высотой тем быстрее, чем тяжелее газ

17. Следствия из барометрической формулы

P
P P0e
Mgh
RT
T = const
Tкр > Tзел> Тсин
h
P убывает с высотой тем быстрее, чем ниже
температура

18.

PV nkT
P P0e
Mgh
RT
Давление концентрации
молекул
n( x) n0e
Uk
U2
U1
Mgh
RT
n0e
U ( x)
kT