Similar presentations:
Молекулярно-кинетическая теория. Идеальный газ. Уравнение молекулярно-кинетической теории идеального газа. Закон Дальтона
1. Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
2. 1. Основные положения молекулярно-кинетической теории и их опытное обоснование. Идеальный газ. Основное уравнение молекулярно-кинетическо
1. Основные положения молекулярнокинетической теории и их опытноеобоснование. Идеальный газ. Основное
уравнение молекулярно-кинетической
теории идеального газа.
Закон Дальтона
3.
Молекулярно-кинетической теорией называетсяучение о строении и свойствах вещества,
использующее представления о существовании
атомов и молекул как наименьших частицах
вещества. В основе теории лежат следующие
утверждения:
1.Все тела состоят из частиц: атомов и молекул;
2.Эти частицы хаотически движутся;
3.Частицы взаимодействуют друг с другом.
4.
Фактом, подтверждающим существование молекул,является возможность определить их массу и размеры
(ионный микроскоп, рентгеноструктурный анализ, массспектроскопия, химический анализ).
Хаотичность движения подтверждается броуновским
движением,
конечной
скоростью
диффузии,
теплопроводности.
Взаимодействие друг с другом частиц носит
электромагнитный характер (силы межмолекулярного
взаимодействия – силы притяжения и отталкивания).
5.
Единица количества вещества называетсямолем. Моль равен количеству вещества,
содержащего столько же частиц, сколько
атомов содержится в 0,012 кг углерода.
Отношение числа молекул N к количеству
вещества называется постоянной Авогадро
NA
N
6, 02 1023 ì î ëü 1
6.
Она показывает, сколько атомов или молекулсодержится в одном моле вещества. Молярная
масса - это масса вещества в количестве
одного моля.
M m0 N A
где m0 - масса одной частицы.
7.
Молярная масса может быть вычислена черезмассу молекулы Mr, измеренную в атомных
единицах массы.
3
M M r 10 кг / моль
8.
Модель идеального газа предполагаетследующее:
молекулы
обладают
пренебрежимо малым объемом, между
молекулами
не
действуют
силы
притяжения, соударение молекул друг с
другом и со стенками сосуда абсолютно
упругие.
9.
На основе использования законов динамики иположений молекулярно-кинетической теории
было получено основное уравнение МКТ.
1
2
p m0n
3
1
2
p
3
где m0 - масса молекулы; n - концентрация
молекул < >2- среднее значение квадрата
скорости молекул; - плотность газа.
2
2
1
2
2
2
... N
N
10.
Обозначив среднее значение кинетическойэнергии поступательного движения Е:
m0
E
2
2
получим
2
p nE
3
11.
Если сосуд заполнили смесью газов, тодавление смеси равно сумме парциальных
давлений газов (закон Дальтона):
p p1 p2 p3 ... p N
.
12.
2. Температура. Связь температуры соскоростью движения молекул.
Температурные шкалы
13.
Состояниесистемы,
при
котором
макроскопические параметры, характеризующие
ее, остаются длительное время неизменными,
называется тепловым равновесием.
14.
Экспериментальные исследования показали,что для любых газов, находящихся в тепловом
равновесии,
отношение
произведения
давления газа на его объем к числу молекул
оказывается одинаковым:
p1V1 p2V2 p3V3
N1
N2
N3
Это позволяет принять величину в качестве
естественной меры температуры.
15.
Так какN
n
V
pV p 2
E
N
n 3
16.
Следовательно, средняя кинетическая энергиямолекул любых газов, находящихся в тепловом
равновесии одинакова. Величина измеряется
в джоулях.
17.
В физике обычно температуру измеряют вградусах, принимая, что температура Т и
величина связаны уравнением
kT
pV
kT
N
18.
Шкала измерения температуры в соответствии сэтим
уравнением
называется
абсолютной
шкалой. Ее предложил английский физик
У.Кельвин. Единица температуры по абсолютной
шкале совпадает с одним градусом по шкале
Цельсия. Расчеты дали значение
k=1,38∙10-23 Дж/К.
k
постоянная
Больцмана.
Знание
коэффициента k позволило установить связь
между абсолютной температурой шкалой и
шкалой Цельсия:
T=t+273.
19.
С введением постоянной Больцмана следуетеще одно из уравнений молекулярнокинетической теории
pV p
kT
N
n
p nkT
20.
Сравнив последнее уравнение с уравнением2
p nE
3
Получим
3
E kT
2
21.
Итак, температура – есть мера среднейкинетическая энергия хаотического движения
молекул газа.
3
E kT
2
22.
Исходя из этого, легко рассчитать среднююквадратичную скорость движения молекул
m0
E
2
2
3
E kT
2
3kT
3RT
3 pV
êâ
m0
M
m
2
Соотношение подтверждено экспериментально
(опыт Штерна).
23.
3. Уравнение состояния идеального газа(уравнение Менделеева-Клапейрона).
Изотермический, изохорный и
изобарный процессы
24.
Используя зависимость давления газа от еготемпературы и концентрации молекул
p nkT
можно
найти
связь
между
основными
макроскопическими
параметрами
газа
объемом V, его давлением p и температурой Т.
Концентрация молекул:
N
n
V
25.
Число молекул газаN N A
m
kT
p
NA
M
V
где R=NAk называется универсальной газовой
постоянной R=8,31 Дж/(моль К). Соотношение
называют уравнением состояния идеального
газа (уравнение Менделеева-Клапейрона).
m
pV
RT
M
26. При неизменной массе газа величина
mR const
M
Поэтому
pV
const
T
27.
Процессы, происходящие при неизменномзначении одного из параметров состояния
называются изопроцессами.
28.
При изотермическом процессепостоянна температура:
(рис.
1)
pV const
p1V1 p 2V2
Эта зависимость называется законом БойляМариотта
(изотерма),
графиком
которой
является гипербола.
29.
При изобарном процессе (рис. 2) постояннодавление. Уравнение имеет вид (закон ГейЛюссака):
V
const
T
V1 V2
T1 T2
Соотношение для давлений: p1>p2.
30.
Выбираяначальное
состояние,
соответствующее Т0=273К, запишем
V0 V
T0 T
1
V
V0T
273
V V0T
V V0 273 t
V V0 1 t
Соотношение связывает объем газа и его температуру
(0С) при изобарном процессе. Где - температурный
коэффициент объемного расширения.
31.
При изохорном процессе (рис. 3) постояненобъем. Уравнение имеет вид (закон Шарля):
p
const
T
p1 p2
T1 T2
Соотношение для объемов: V1>V2.
32.
Выбирая начальное состояние, соответствующееТ0=273К, запишем
p p0 1 t
Соотношение связывает давление газа и его
температуру (0С) при изобарном процессе. Где температурный коэффициент давления газа.














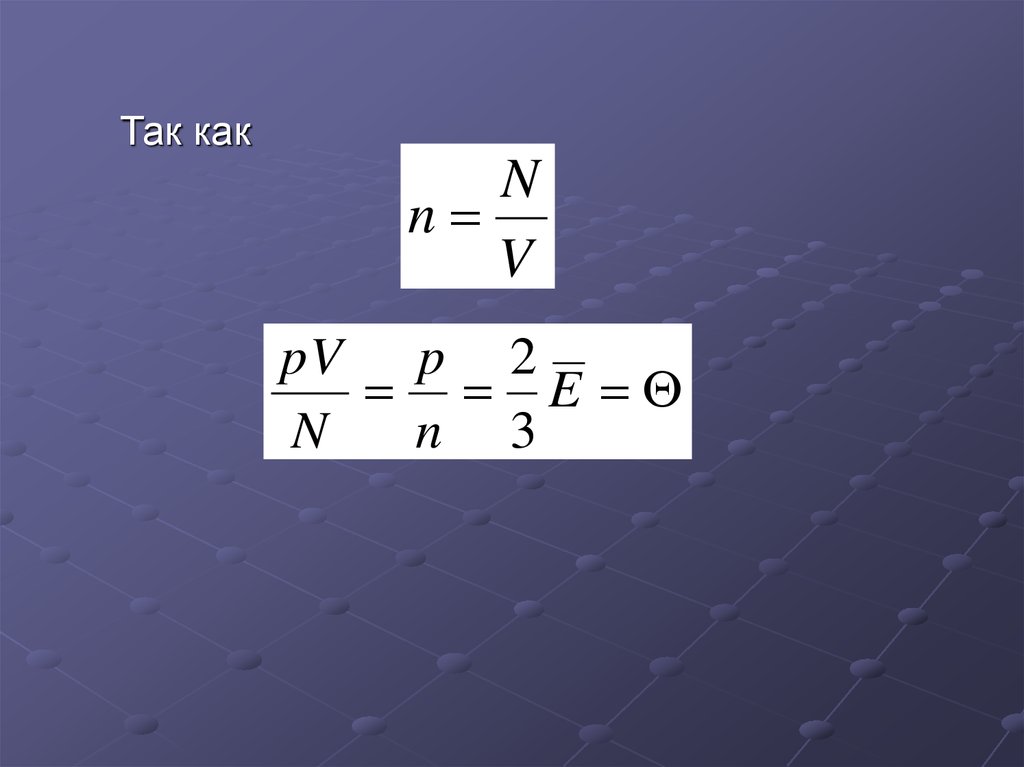

















 physics
physics








