Similar presentations:
Основы молекулярно-кинетической теории
1.
CEEЛекция
Составители: д.т.н., профессор Симдянкин А.А., к.п.н., доцент Симдянкина Е.Е.
2.
Основы МКТCEE
Левкип и Демокрит – 400 лет до н.э.
М.В. Ломоносов – XVIII век.
«О причине теплоты и холода» и
«О коловратном движении корпускул»
3.
Основы МКТCEE
Молекулярно-кинетической теорией
называют учение о строении и
свойствах вещества на основе
представления о существовании
атомов и молекул как наименьших
частиц химического вещества.
4.
Основные положения МКТCEE
1. Все вещества – жидкие,
твердые и газообразные –
образованы из мельчайших
частиц – молекул (атомов),
которые сами состоят из
более мелких элементарных
частиц (электронов,
протонов, нейтронов).
5.
Основные положения МКТCEE
2. Атомы и молекулы
находятся в
непрерывном
хаотическом
движении.
6.
Основные положения МКТCEE
3. Частицы взаимодействуют друг с другом
силами, имеющими электрическую природу.
H
He
– -е
е
+
2е
++
-е –
– -е
Li
-е –
– -е
+ 3е
++
– -е
Гравитационное взаимодействие между частицами пренебрежимо мало.
7.
Опытные обоснования МКТСуществование молекул
CEE
1. Закон кратных отношений:
при образовании из двух элементов
различных веществ массы одного из
элементов в разных соединениях
находятся в кратных отношениях
N2 O : N2 O2 : N 2 O3 = 1 : 2 : 3
8.
Опытные обоснования МКТСуществование молекул
CEE
7 г азота, соединяясь с 4 г кислорода, образуют
11 г закиси азота N2O,
8 г » » » 15 г окиси азота NО,
12 г » » » 19 г азотистого ангидрида N2О3,
16 г » » » 23 г двуокиси азота NO2,
20 г » » » 27 г азотного ангидрида N2О5.
Массы кислорода, приходящиеся на одну и ту же
массу азота (7 г), в этих соединениях относятся как
4 : 8 : 12 : 16 : 20 = 1 : 2 : 3 : 4 : 5.
9.
Опытные обоснования МКТСуществование молекул
CEE
2. Молекулы
наблюдаются с
помощью ионного
проектора,
электронного
микроскопа
Современный
электронный микроскоп
10.
Опытные обоснования МКТВзаимодействие молекул
CEE
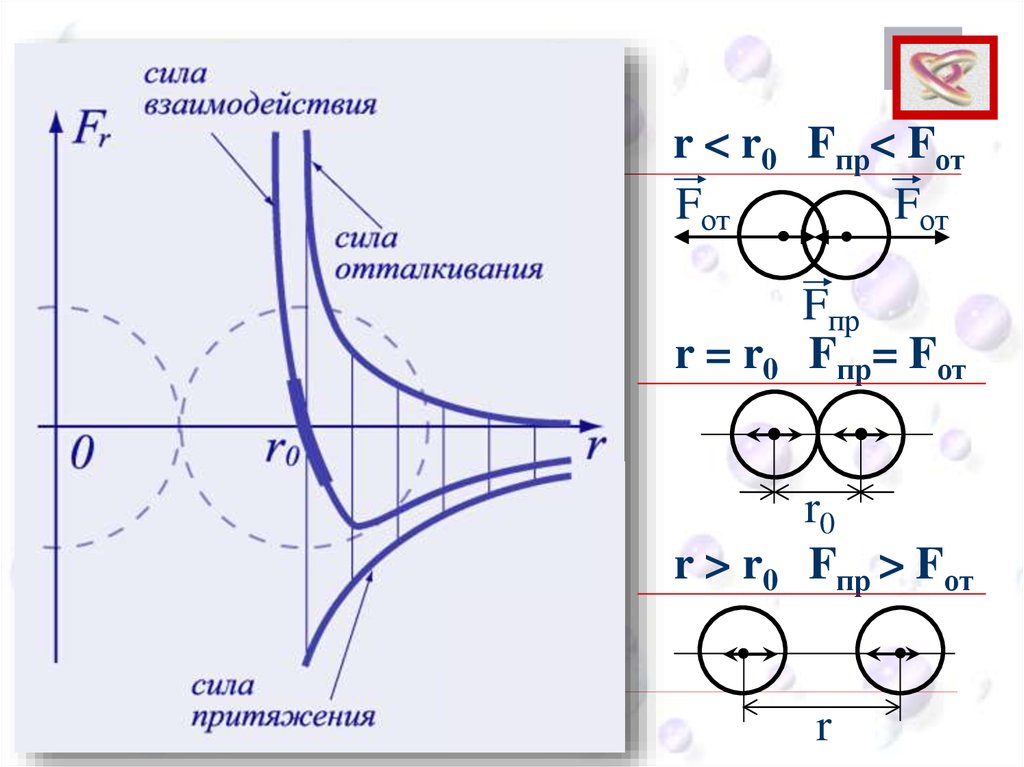
Силы притяжения и
отталкивания действуют
одновременно.
Силы электромагнитной природы.
11.
CEEr < r0 Fпр< Fот
Fот
Fот
Fпр
r = r0 Fпр= Fот
r0
r > r0 Fпр > Fот
r
12.
Опытные обоснования МКТХаотическое движение молекул
CEE
Наиболее ярким экспериментальным
подтверждением представлений
молекулярно-кинетической теории
о беспорядочном движении атомов и молекул
является броуновское
движение.
13.
Опытные обоснования МКТХаотическое движение молекул
CEE
Фотография броуновского движения
14.
Опытные обоснования МКТХаотическое движение молекул
CEE
1. Броуновское движение.
2. Диффузия.
3. Давление газа на стенки сосуда.
4. Стремление газа занять любой объем.
15.
Основы МКТCEE
Беспорядочное хаотическое
движение молекул называется
тепловым движением.
Кинетическая энергия теплового
движения растет с возрастанием
температуры.
Внутренняя энергия — это сумма энергий
молекулярных взаимодействий и энергии
теплового движения молекул.
Понятие энергии относится всегда к системе тел.
16.
Основы МКТCEE
17.
Основы МКТCEE
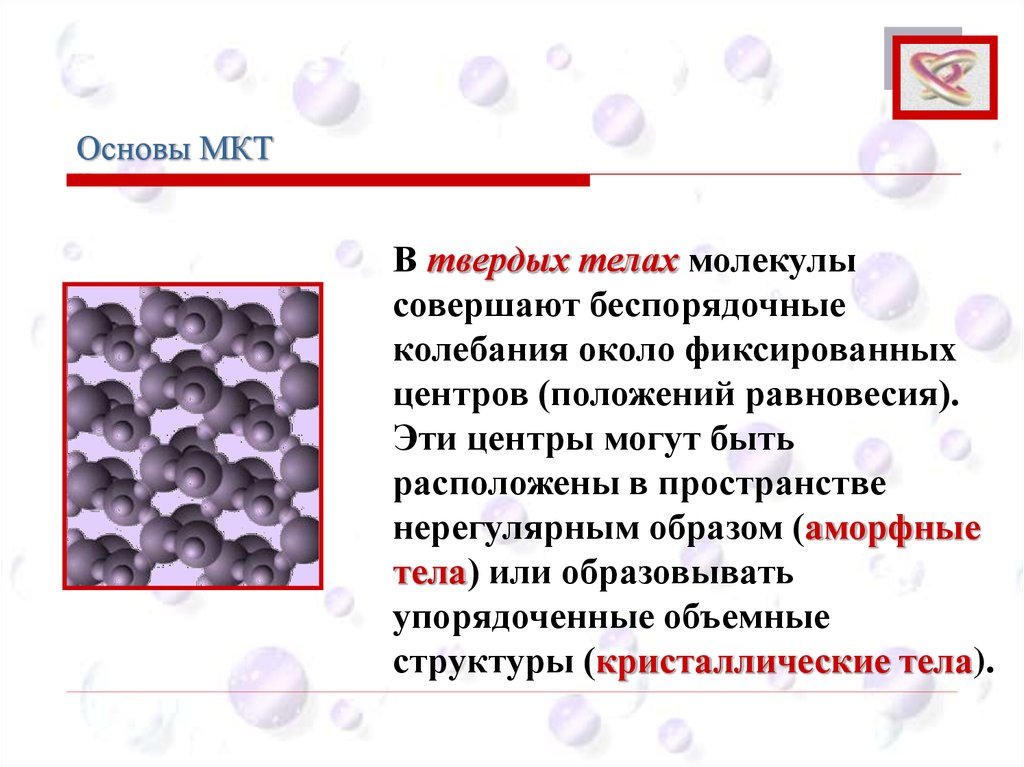
В твердых телах молекулы
совершают беспорядочные
колебания около фиксированных
центров (положений равновесия).
Эти центры могут быть
расположены в пространстве
нерегулярным образом (аморфные
тела) или образовывать
упорядоченные объемные
структуры (кристаллические тела).
18.
Основы МКТCEE
В жидкостях молекулы имеют
значительно большую свободу
для теплового движения. Они
не привязаны к определенным
центрам и могут перемещаться
по всему объему жидкости.
Этим объясняется текучесть
жидкостей.
19.
Основы МКТCEE
В
газах
расстояния
между
молекулами обычно значительно
больше
их
размеров.
Силы
взаимодействия между молекулами
на таких больших расстояниях
малы, и каждая молекула движется
вдоль прямой линии до очередного
столкновения с другой молекулой
или со стенкой сосуда.
20.
Идеальный газCEE
Простейшей моделью молекулярно-кинетической
теории является модель идеального газа.
В кинетической модели идеального газа молекулы
рассматриваются как идеально упругие шарики,
взаимодействующие между собой и со стенками
только во время упругих столкновений.
21.
Идеальный газCEE
Суммарный объем всех молекул предполагается
малым по сравнению с объемом сосуда, в котором
находится газ.
Модель идеального газа достаточно хорошо
описывает поведение реальных газов в широком
диапазоне давлений и температур.
22.
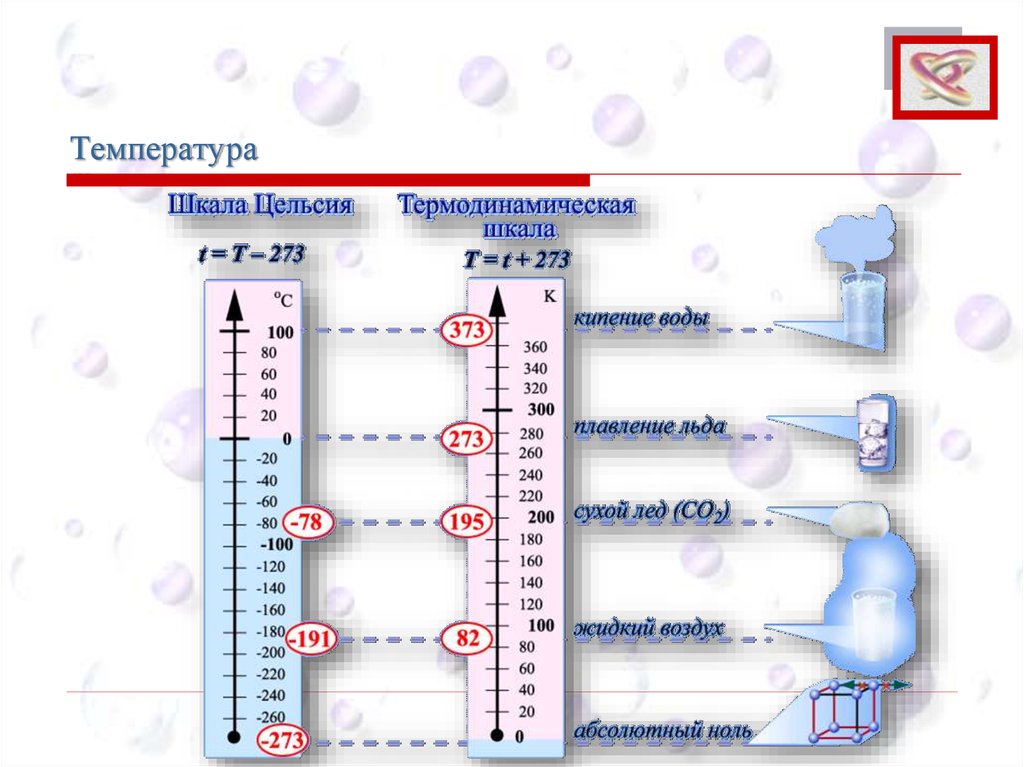
ТемператураCEE
Температурная шкала Кельвина называется абсолютной
(термодинамической) шкалой температур.
T = t + 273,15
В СИ единицей измерения температуры является кельвин - K.
Комнатная температура TС = 20 °С по шкале Кельвина равна
TК = 293,15 К.
23.
ТемператураCEE
24.
ТемператураCEE
Понятие температуры
теплового равновесия.
тесно
связано
с
понятием
Тепловое равновесие – это такое состояние системы тел,
находящихся в тепловом контакте, при котором не
происходит теплопередачи от одного тела к другому, и все
макроскопические параметры тел остаются неизменными.
Температура – это физический параметр, одинаковый для
всех тел, находящихся в тепловом равновесии.
25.
Основы МКТCEE
Макроскопические параметры:
давление,
объем,
p V T
температура.
?
26.
CEE27.
ИЗОПРОЦЕССЫ В ГАЗАХ(газовые законы)
CEE
Процессы,
протекающие при
неизменном значении
одного из параметров
(p, V, T) для данной
массы газа, называют
изопроцессами.
28.
Изотермический процесс(закон Бойля-Мариотта)
CEE
Для данной массы газа при постоянной
температуре произведение давления газа на его
объем есть величина постоянная:
1662 г.
Бойль (англ.)
При
T = const; m = const
pV =const
1676 г. Мариотт(фр.)
p1 V2
p2 V1
29.
Изотермический процесс(закон Бойля-Мариотта)
CEE
График
процесса:
p
T2 > T1
T1
изотерма
V
p
Т1
Т2
Т
V
Т1
Т2
Т
30.
Прикольный процесс(закон Бойля-Мариотта)
CEE
При T = const;
m = const
pV =const
p1 V2
p2 V1
31.
Изобарный процесс(закон Гей-Люссака)
CEE
Объем данной массы газа при постоянном
давлении изменяется линейно с температурой:
При p = const; m = const
V = V0 (1 + αt)
Изобарным процессом называют процесс, протекающий при неизменном
давлении p.
32.
Изобарный процесс(закон Гей-Люссака)
CEE
V = V0 (1 + αt)
где V0 – объем газа при температуре 0 °С.
Коэффициент α равен (1/273,15) К–1.
Его называют температурным
коэффициентом объемного расширения газов.
В термодинамической
форме:
V1
T1
V2
T2
33.
Изобарный процесс(закон Гей-Люссака)
CEE
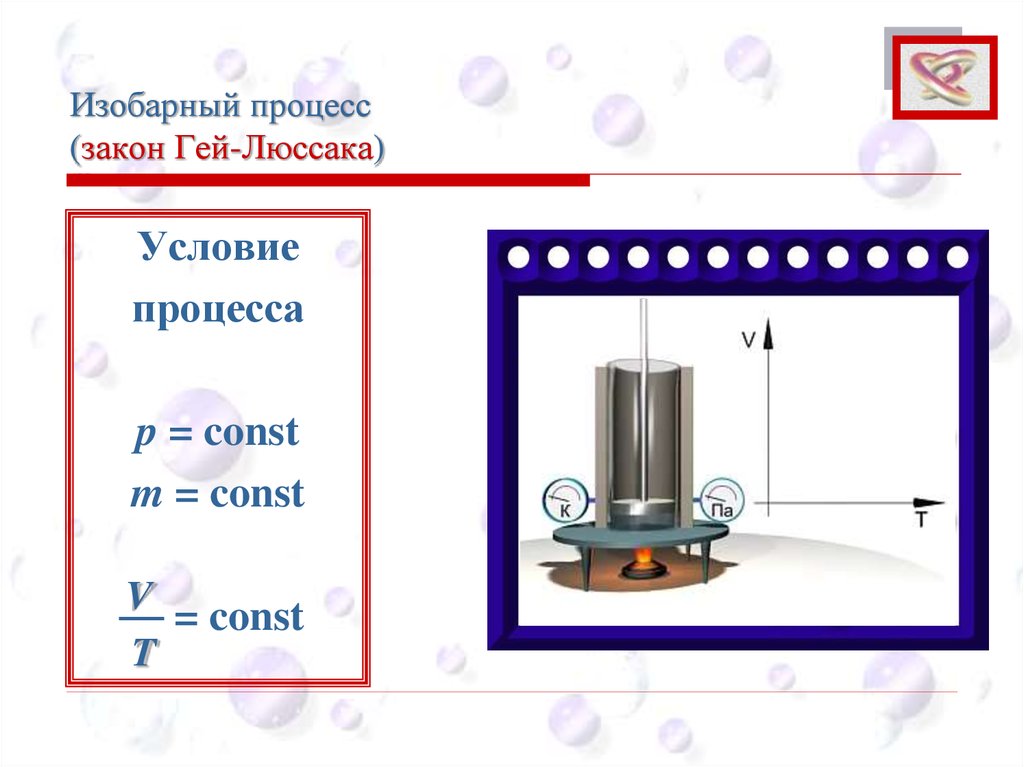
Условие
процесса
p = const
m = const
V
= const
T
p
p
p2 > p1
График
процесса:
p1
изобара
V
p2
p1
Т
V
p1
p2 > p1
Т
34.
Изобарный процесс(закон Гей-Люссака)
CEE
Условие
процесса
p = const
m = const
V
= const
T
35.
Изохорный процесс(закон Гей-Люссака – Шарля)
CEE
Давление
газа
p
изменяется
прямо
пропорционально его абсолютной температуре:
При V = const; m = const
p = p 0 (1 + αt)
Изохорный процесс – это процесс протекающий при постоянном объеме V.
36.
Изохорный процесс(закон Гей-Люссака – Шарля)
CEE
p = p 0 (1 + αt)
где p0 – давление газа при температуре 0 °С.
Коэффициент α равен (1/273,15) К–1.
Его называют температурным
коэффициентом давления.
В термодинамической
форме:
p1
T1
p2
T2
37.
Изохорный процесс(закон Гей-Люссака – Шарля)
CEE
p
Условие
процесса
V = const
m = const
p
= const
T
График
процесса:
V1
V
изохора
V2
V
V2
V1
Т
p
V1
V2 > V1
Т
38.
Изохорный процесс(закон Гей-Люссака – Шарля)
CEE
Условие
процесса
V = const
m = const
p
= const
T
39.
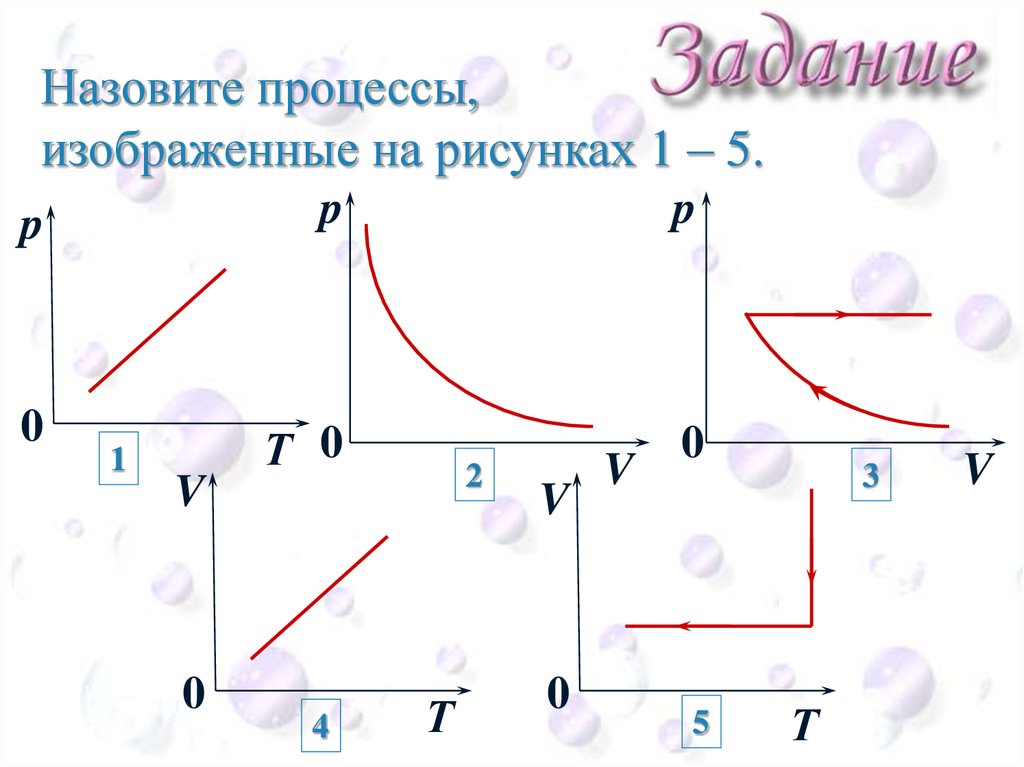
Назовите процессы,изображенные на рисунках 1 – 5.
CEE
p
0
1
V
0
p
p
Т 0
0
4
2
Т
V
0
V
5
3
Т
V
40.
Уравнение КлапейронаCEE
Клапейрон (фр.)
вывел уравнение
состояния
идеального газа,
объединив законы
Бойля-Мариотта и
закон Гей-Люссака
– Шарля.
p
p1
1 (p1, V1, T1)
p1
p2
0
V1
1′ (p1 ,V2 ,T1 )
2 (p2, V2, T2)
V2 V
41.
Уравнение КлапейронаCEE
Из рис. видим:
p1V1 p1 V2
p1 T1
p2 T2
p
p1
1 (p1, V1, T1)
p1
p2
0
V1
Исключим p1 .
1′ (p1 ,V2 ,T1 )
2 (p2, V2, T2)
V2 V
42.
Уравнение КлапейронаCEE
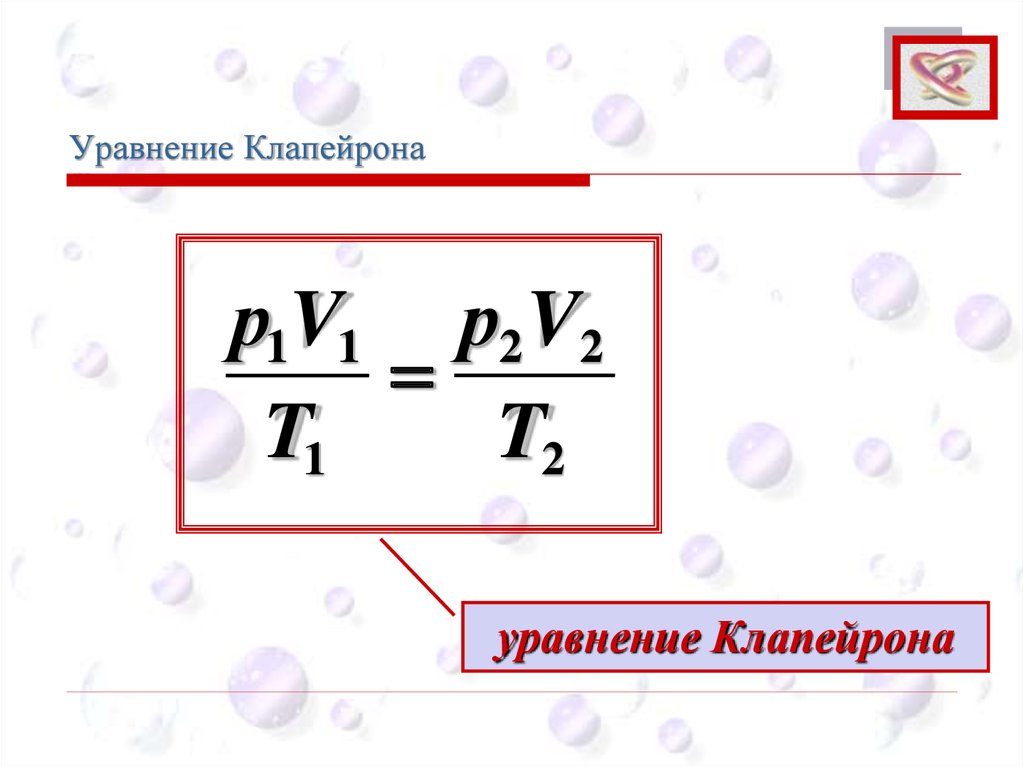
р1V1 р2 V2
T1
T2
уравнение Клапейрона
43.
Уравнение КлапейронаCEE
(1)
44.
Уравнение Менделеева-КлапейронаCEE
Менделеев объединил уравнение Клапейрона с
законом Авогадро.
Согласно закону Авогадро:
Один моль любого газа при нормальных
условиях (Т = 273 К и р = 1,013∙105 Па)
занимает один и тот же объем (молярный)
Vm, равный:
Vm = 0,0224 м3/моль = 22,41 ∙ 10-3 м3/моль.
Подставим эти данные в (1):
45.
Уравнение Менделеева-КлапейронаCEE
p Vm
Дж
const R
8,31
T
моль К
46.
Уравнение Менделеева-КлапейронаCEE
(молярная газовая постоянная)
47.
Уравнение Менделеева-КлапейронаCEE
Тогда для 1 моль газа уравнение (1)
можно записать в виде:
pVm R T
(2)
Уравнение МенделееваКлапейрона для 1 моль газа
48.
Уравнение Менделеева-КлапейронаCEE
Тогда для любой массы газа m:
m
pV
RT RT
M
m
Vm
Учтено, что: V
M
ν – (количество вещества) число молей газа.
49.
Уравнение Менделеева-КлапейронаCEE
50.
Основы МКТCEE
Задача молекулярно-кинетической теории
состоит в том, чтобы установить связь между
микроскопическими (масса, скорость,
кинетическая энергия молекул) и
макроскопическими параметрами
(давление, объем, температура).
m ʋ Eк
?
p V T
51.
CEEГаз, состоящий из отдельных атомов, а не
молекул, называют одноатомным.
К одноатомным газам относят инертные газы —
гелий, неон, аргон. В случае идеальных газов
пренебрегают силами взаимодействия молекул, т. е.
их потенциальная энергия полагается равной нулю,
поэтому внутренняя энергия идеального газа
представляет собой кинетическую энергию теплового
движения молекул.
52.
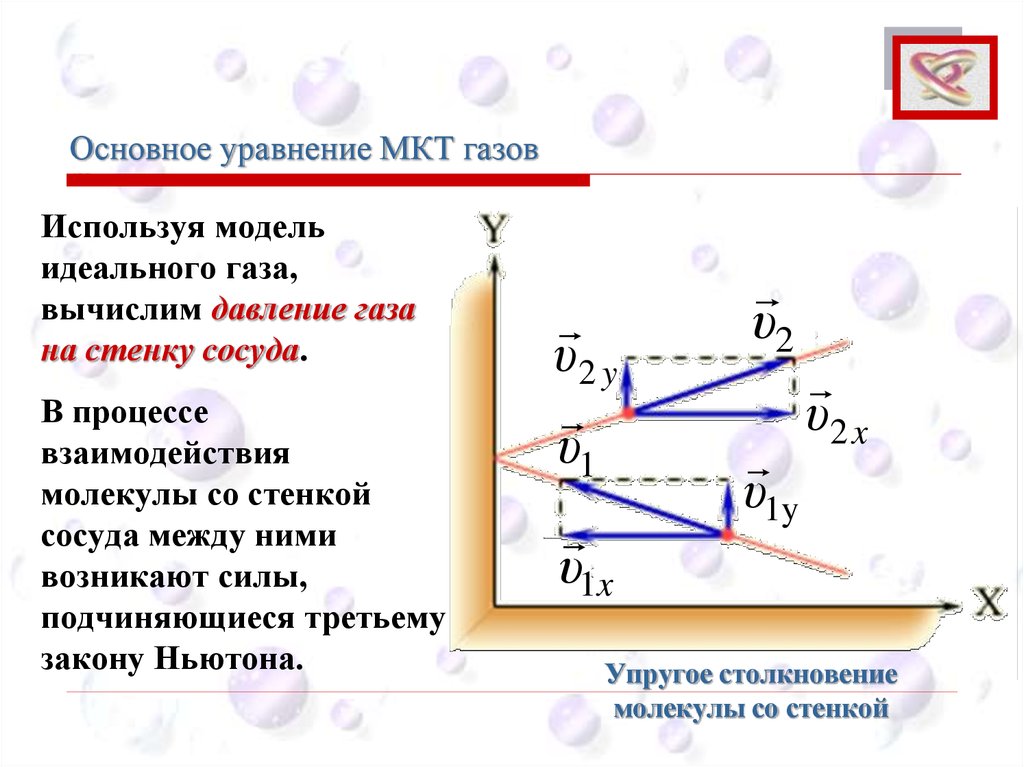
Основное уравнение МКТ газовCEE
Используя модель
идеального газа,
вычислим давление газа
на стенку сосуда.
В процессе
взаимодействия
молекулы со стенкой
сосуда между ними
возникают силы,
подчиняющиеся третьему
закону Ньютона.
υ2 y
υ1
υ1x
υ2
υ1y
υ2 x
Упругое столкновение
молекулы со стенкой
53.
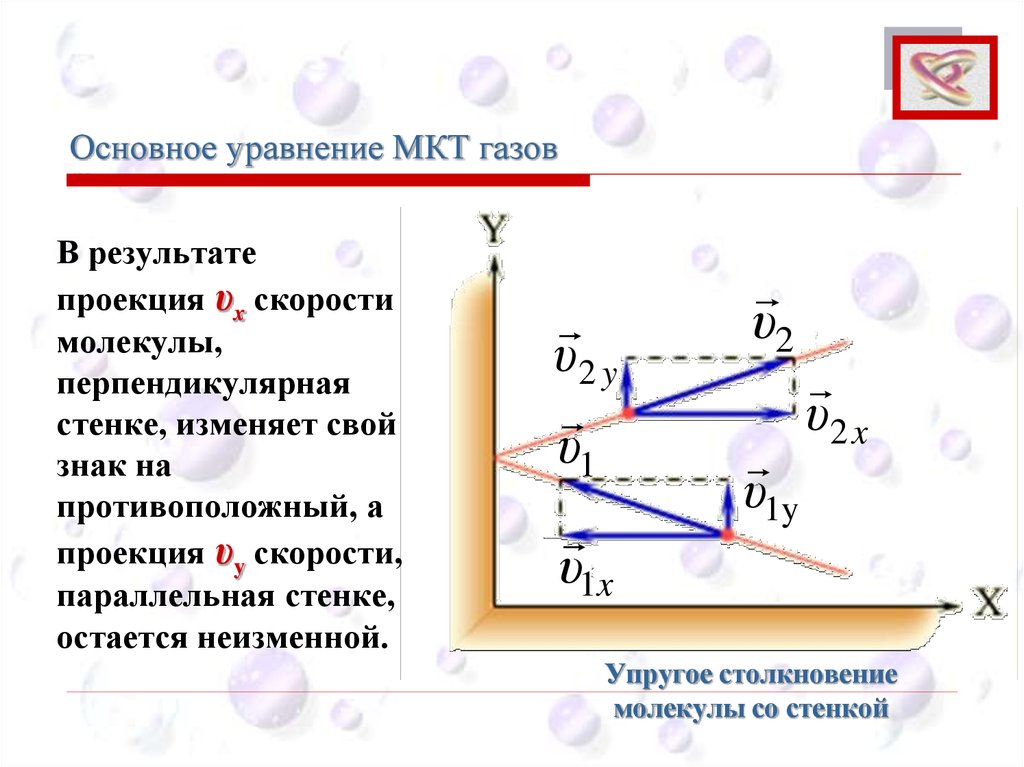
Основное уравнение МКТ газовCEE
В результате
проекция υx скорости
молекулы,
перпендикулярная
стенке, изменяет свой
знак на
противоположный, а
проекция υy скорости,
параллельная стенке,
остается неизменной.
υ2 y
υ1
υ1x
υ2
υ1y
υ2 x
Упругое столкновение
молекулы со стенкой
54.
Основное уравнение МКТ газовCEE
z
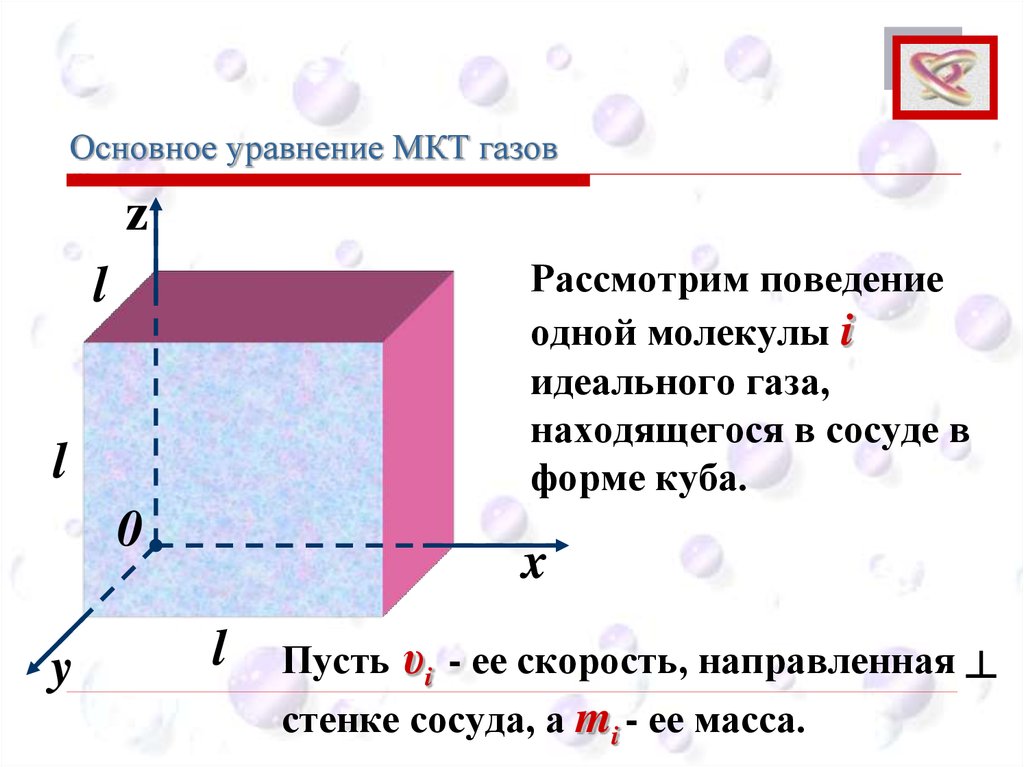
Рассмотрим поведение
одной молекулы i
идеального газа,
находящегося в сосуде в
форме куба.
l
l
0
y
x
l
Пусть υi - ее скорость, направленная ┴
стенке сосуда, а mi - ее масса.
55.
Основное уравнение МКТ газовCEE
z
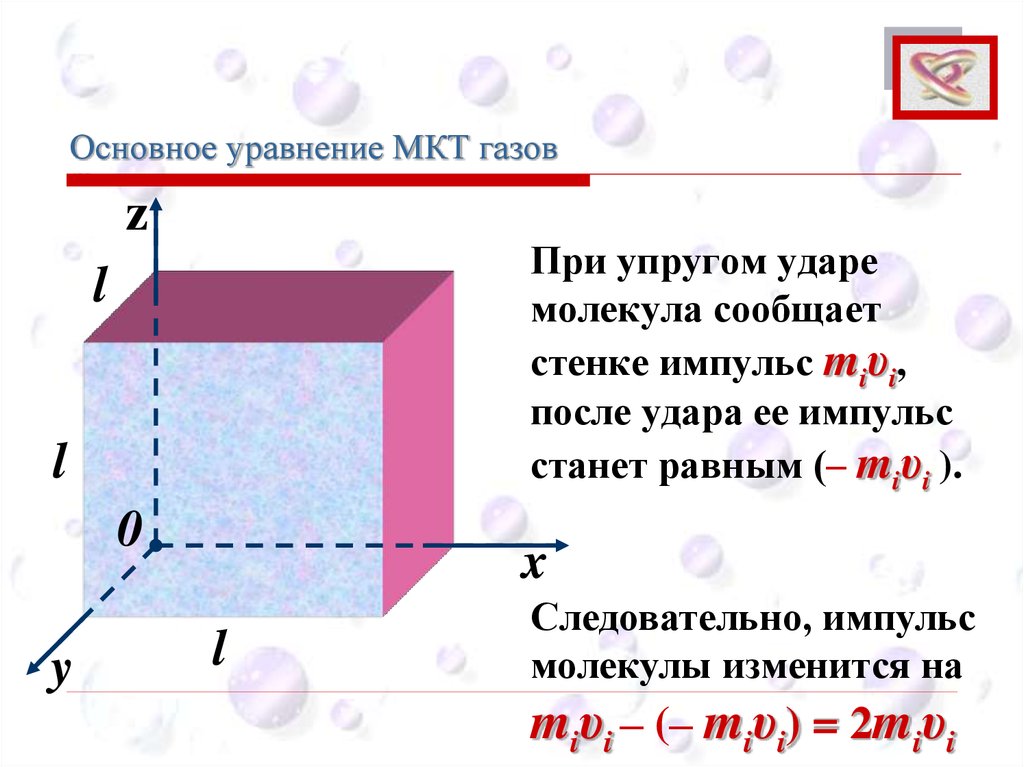
При упругом ударе
молекула сообщает
стенке импульс miυi,
после удара ее импульс
станет равным (– miυi ).
l
l
0
y
x
l
Следовательно, импульс
молекулы изменится на
miυi – (– miυi) = 2miυi
56.
Основное уравнение МКТ газовCEE
z
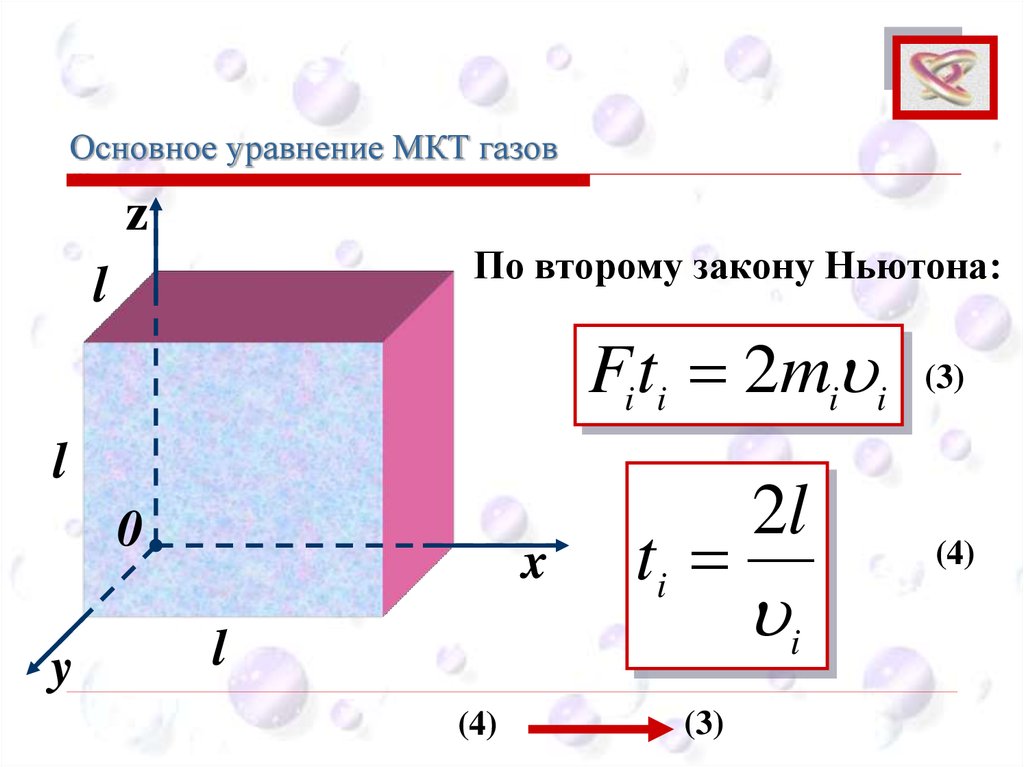
По второму закону Ньютона:
l
Fiti 2mi i
l
0
y
x
ti
l
(4)
(3)
2l
i
(3)
(4)
57.
Основное уравнение МКТ газовCEE
z
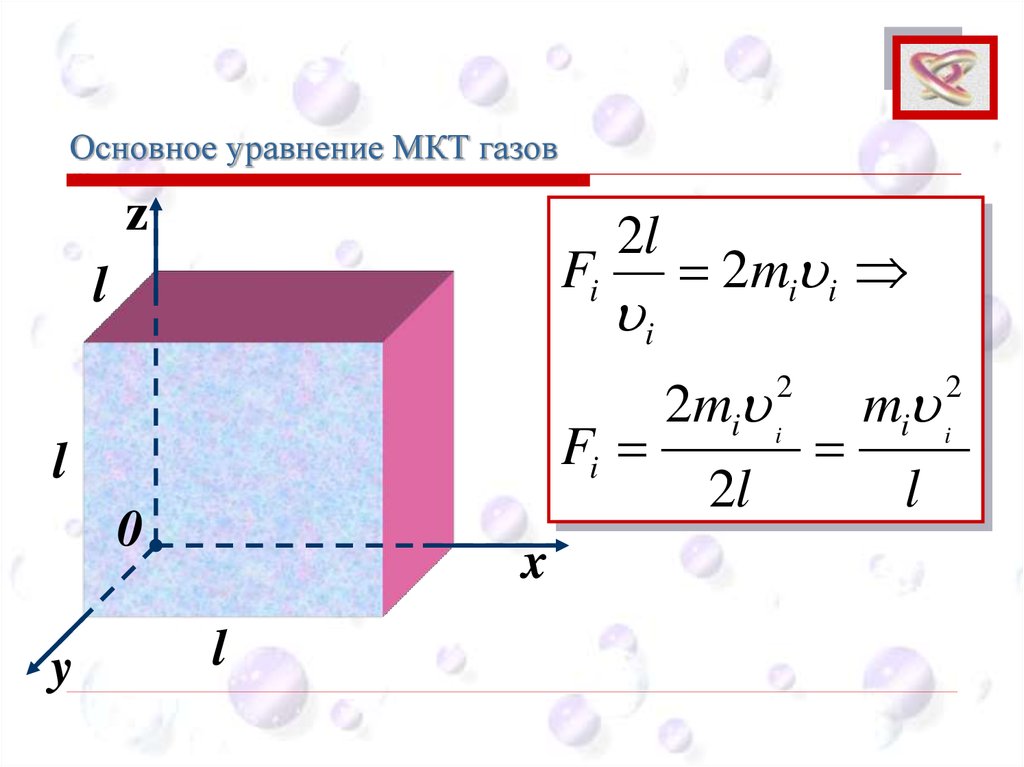
Fi
l
2l
i
2mi i
2mi i
2
Fi
l
0
y
x
l
2l
mi i
2
l
58.
Основное уравнение МКТ газовCEE
z
l
N
3
l
0
y
N
3
N
3
x
l
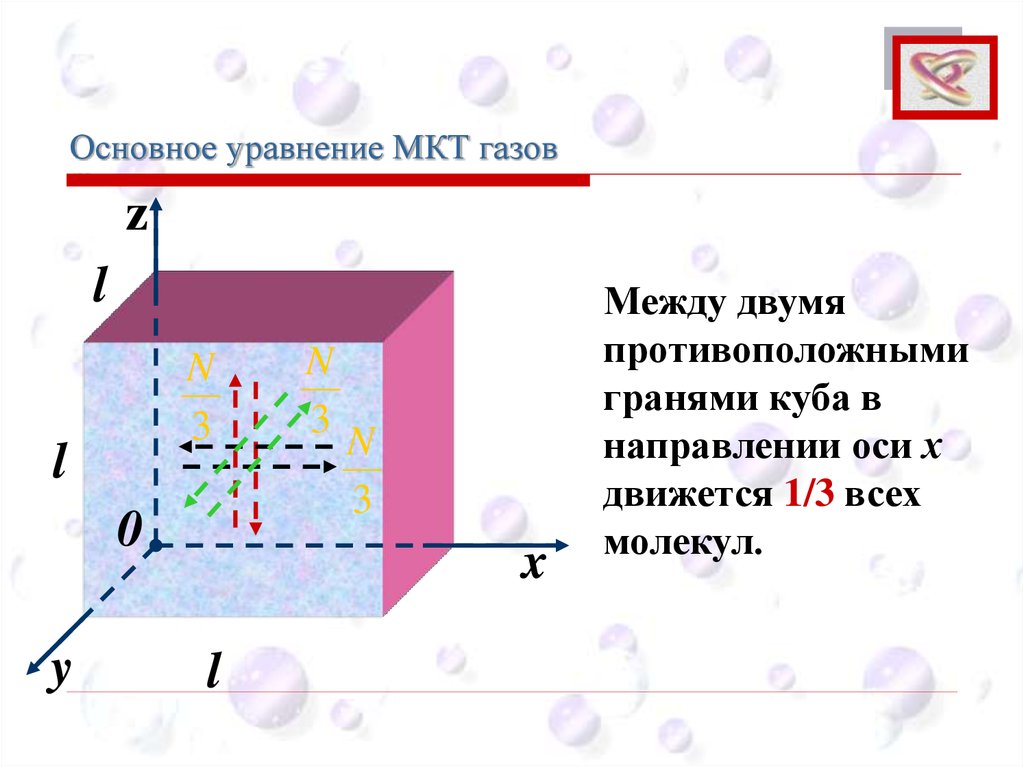
Между двумя
противоположными
гранями куба в
направлении оси х
движется 1/3 всех
молекул.
59.
Основное уравнение МКТ газовCEE
Суммарная сила ударов об одну грань:
1 m
m2
mn
F
...
3 l
l
l
2
1 1
2
2
2
n
60.
Основное уравнение МКТ газовCEE
Для идеального газа (m1 = m2 = … = mn = m0):
1 m0 2
2
2
1 2 ... n
F
3 l
или
1 m0 N ...
F
3 l
N
2
1
2
2
кв
2
n
2
61.
Основное уравнение МКТ газовCEE
1 m0 N
F
кв
3 l
2
С другой стороны, сила F, действующая со стороны
газа в направлении, перпендикулярном к
поверхности S стенки сосуда:
F pS
H
p 1Па 1 2
м
р – давление газа на стенку сосуда.
62.
Основное уравнение МКТ газовCEE
В нашем случае
S l
2
Следовательно,
F F 1 m0 N
p 2
кв
3
S l
3 l
2
63.
Основное уравнение МКТ газовCEE
Или
1 m0 N
p
кв
3 V
2
1
m0 n кв
3
Основное уравнение МКТ
n
N
‒ концентрация молекул
V
2
(5)
64.
Основное уравнение МКТ газовCEE
Средняя кинетическая энергия хаотического движения
молекул газа
1
E m0 кв
2
Откуда
кв
2
2
2E
m0
(5)
65.
Основное уравнение МКТ газовCEE
1
p m0 n кв
3
2
2E
1
2
m0 n
nE
3
m0
3
(6)
Основное уравнение МКТ
66.
Основное уравнение МКТ газовCEE
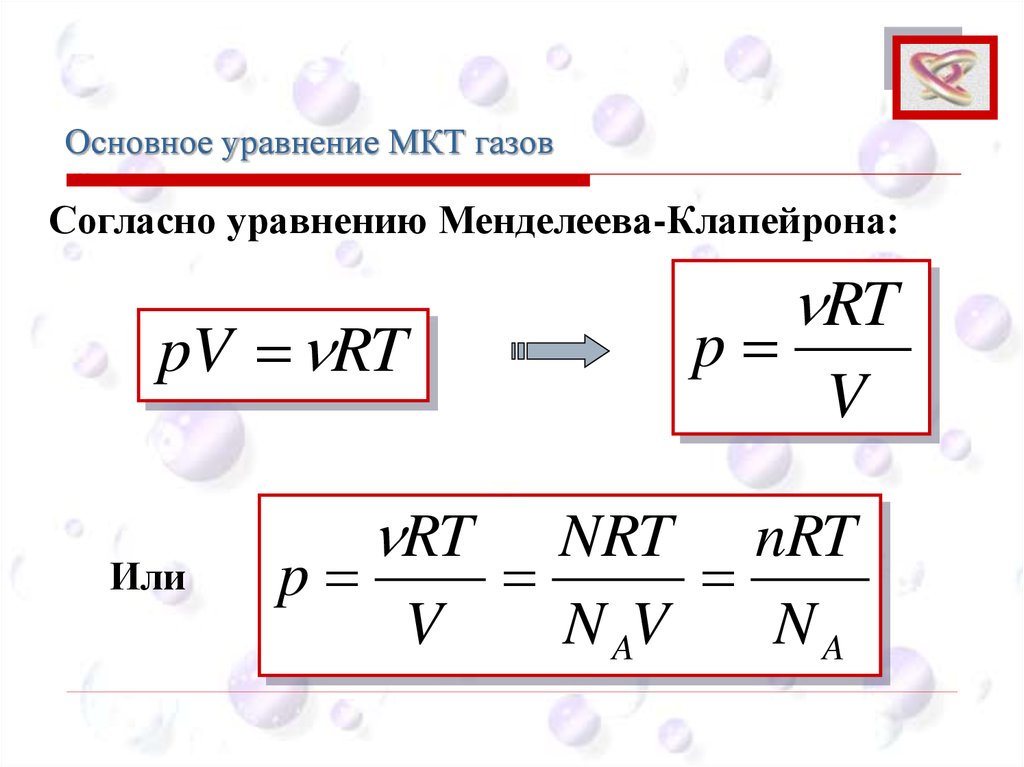
Согласно уравнению Менделеева-Клапейрона:
pV RT
Или
RT
p
RT
V
NRT nRT
p
V
N AV
NA
67.
Основное уравнение МКТ газовCEE
С другой стороны:
Тогда:
2
p n E
3
2
nRT
n E
3
NA
Откуда:
nRT 3 3 R
E
T
N A 2n 2 N A
68.
Основное уравнение МКТ газовCEE
R
k
NA
69.
Основное уравнение МКТ газовCEE
Тогда:
3
E kT
2
(7)
Средняя кинетическая энергия хаотического
движения молекул газа прямо пропорциональна
абсолютной температуре.
Температура есть мера средней кинетической
энергии поступательного движения молекул.
70.
Основное уравнение МКТ газовCEE
(7)
(6)
2
2 3
p n E n kT
3
3 2
Или
p = nkT
71.
CEEЛекцию подготовили д.т.н.,
профессор Симдянкин А.А.,
к.п.н., доцент Симдянкина Е.Е.

























































 physics
physics








