Пирамида. Её элементы. Правильная пирамида. Усечённая пирамида

1. Пирамида

Её элементы.
Правильная пирамида.
Усечённая пирамида

2.

S – вершина пирамиды
ABCDE – основание пирамиды
S
Вершина
пирамиды
Основание
пирамиды
B
A
C
E
D

3.

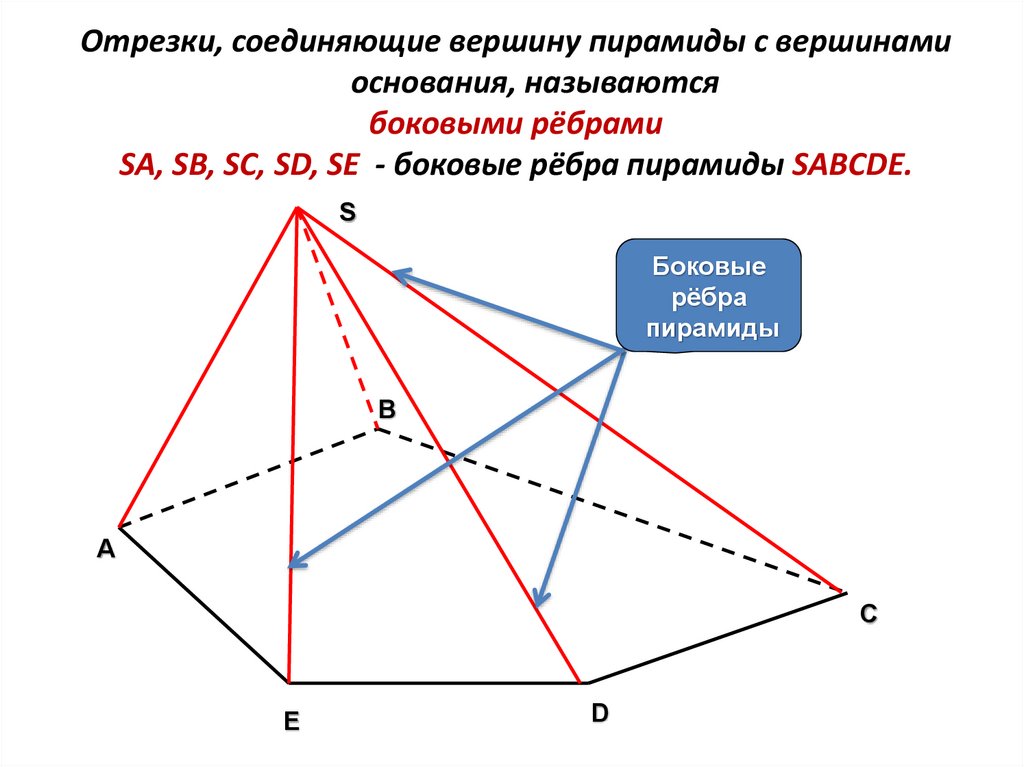
Отрезки, соединяющие вершину пирамиды с вершинами
основания, называются
боковыми рёбрами
SA, SB, SC, SD, SE - боковые рёбра пирамиды SABCDЕ.
S
Боковые
рёбра
пирамиды
B
A
C
E
D

4.

Высотой пирамиды называется перпендикуляр, опущенный
из вершины пирамиды на плоскость основания.
SО - высота пирамиды SABCDЕ.
S
Высота
пирамиды
B
A
О
C
E
D

5.

F
S
C
P
K
O
M
B
A
N
O
M
C
P
R
K
S
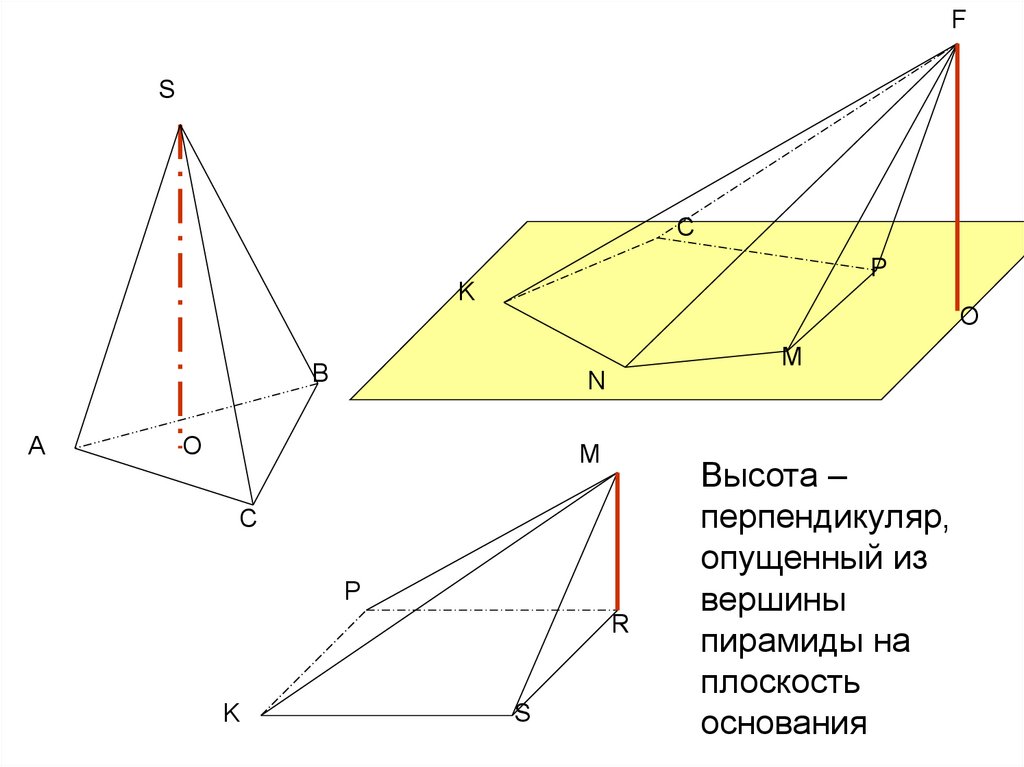
Высота –
перпендикуляр,
опущенный из
вершины
пирамиды на
плоскость
основания

6.

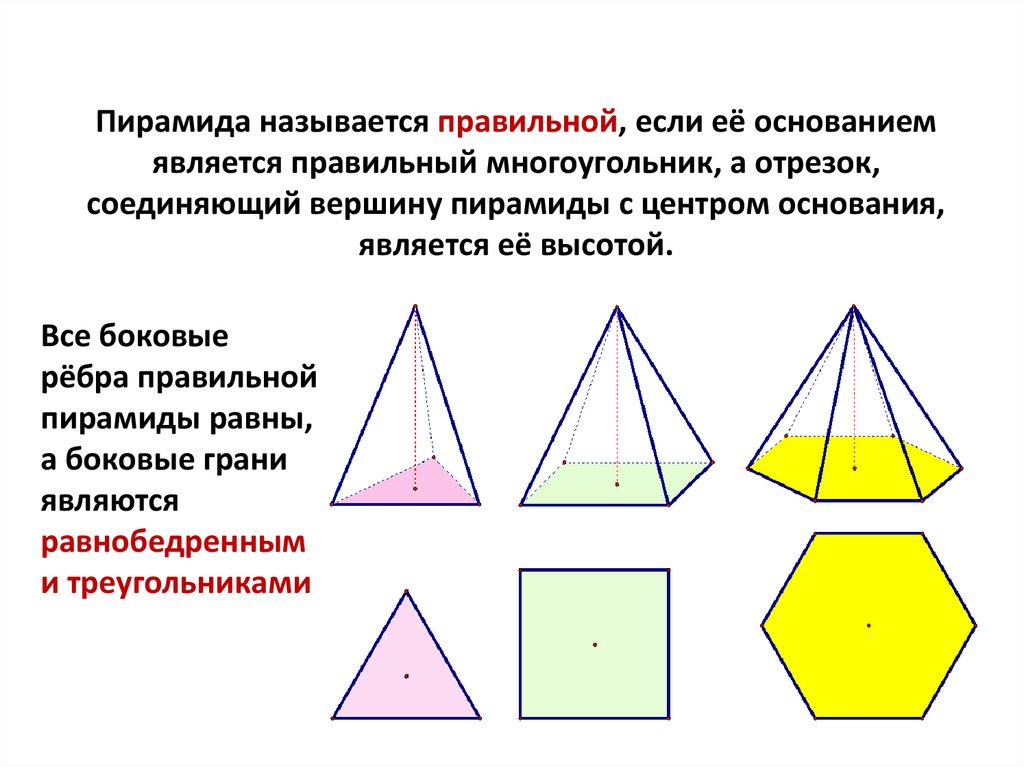
Пирамида называется правильной, если её основанием
является правильный многоугольник, а отрезок,
соединяющий вершину пирамиды с центром основания,
является её высотой.
Все боковые
рёбра правильной
пирамиды равны,
а боковые грани
являются
равнобедренным
и треугольниками

7.

8.

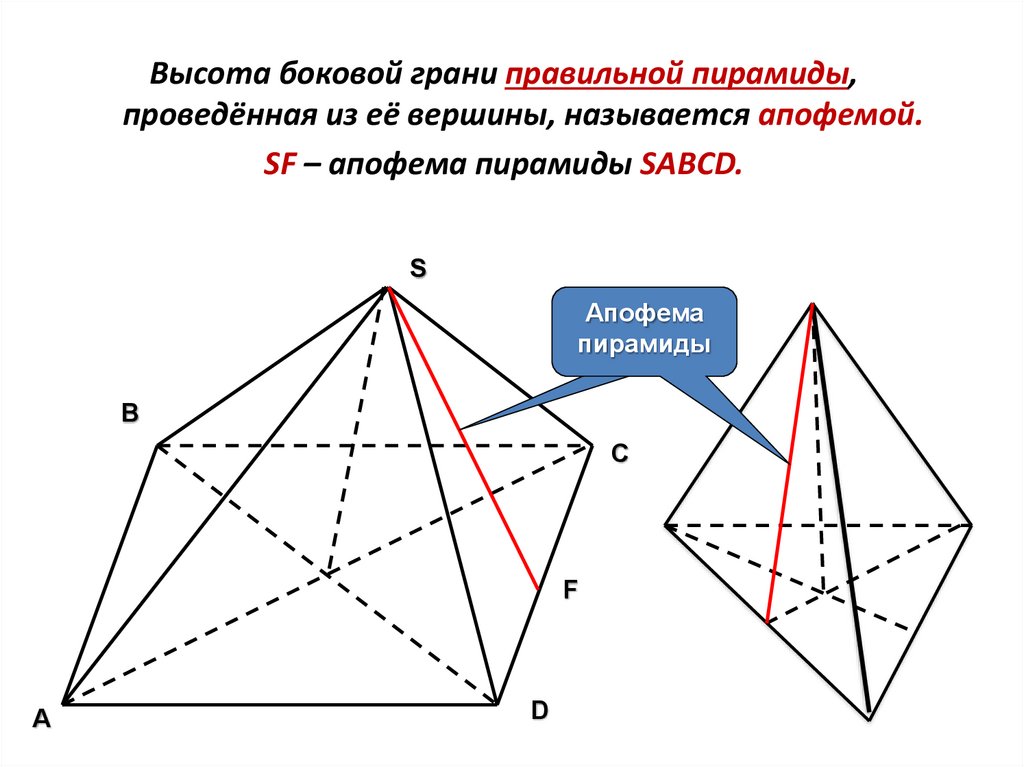
Высота боковой грани правильной пирамиды,
проведённая из её вершины, называется апофемой.
SF – апофема пирамиды SABCD.
S
Апофема
пирамиды
B
С
F
A
D

9.

Осью правильной пирамиды называется прямая,
содержащая её высоту.
Ось
пирамиды

10.

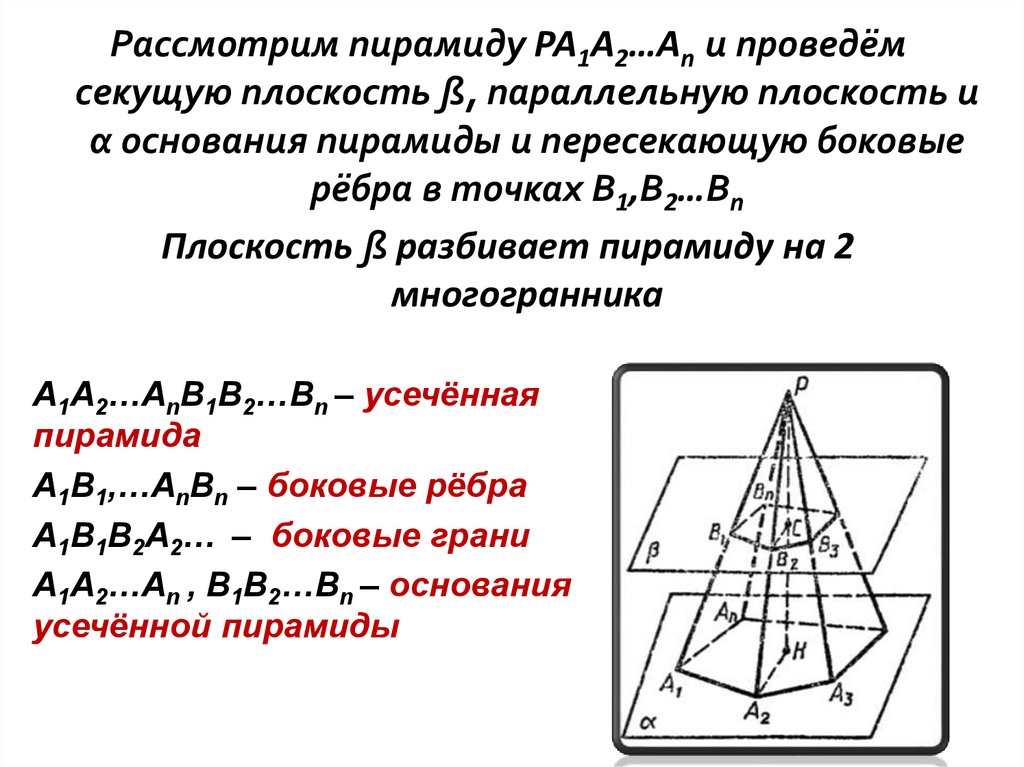
Рассмотрим пирамиду PA1A2…An и проведём
секущую плоскость ß, параллельную плоскость и
α основания пирамиды и пересекающую боковые
рёбра в точках В1,В2…Вn
Плоскость ß разбивает пирамиду на 2
многогранника
A1A2…AnВ1В2…Вn – усечённая
пирамида
A1В1,…AnВn – боковые рёбра
A1В1В2A2… – боковые грани
A1A2…An , В1В2…Вn – основания
усечённой пирамиды

11.

Усечённая пирамида называется
правильной, если она получена сечением
правильной пирамиды плоскостью,
параллельной основанию.

12.

Боковой поверхностью пирамиды называется
сумма площадей её боковых граней.
Площадь полной поверхности пирамиды
равна сумме площади боковой поверхности
и площади основания:
S пол Sбок Sосн

13.

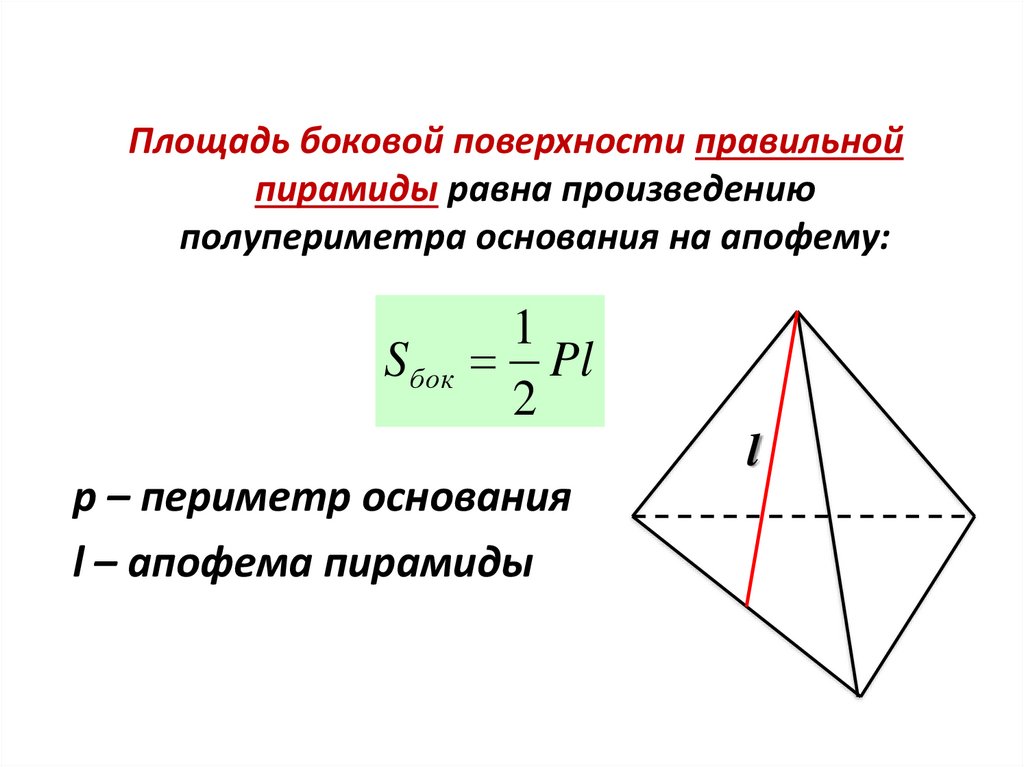
Площадь боковой поверхности правильной
пирамиды равна произведению
полупериметра основания на апофему:
S бок
1
Pl
2
l
p – периметр основания
l – апофема пирамиды

14.

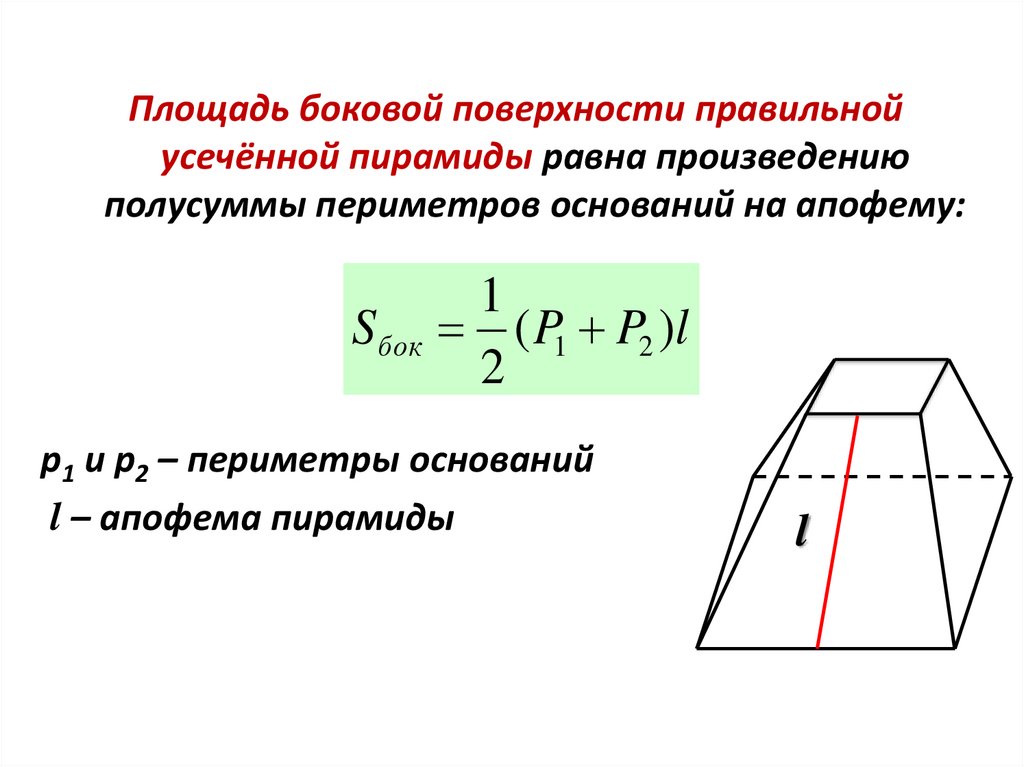
Площадь боковой поверхности правильной
усечённой пирамиды равна произведению
полусуммы периметров оснований на апофему:
S бок
1
( P1 P2 )l
2
p1 и p2 – периметры оснований
l – апофема пирамиды
l

15.

Задача № 1. Основанием пирамиды DABC является прямоугольный
треугольник ABC, у которого гипотенуза AB=29 см, а катет АС=21 см. Боковое
ребро DA перпендикулярно к плоскости основания и равно 20 см.
Найдите площадь боковой поверхности пирамиды.
Решение:
D
Найти: Sбок
Треугольники ADC, ADB, DCB – прямоугольные
20
29
A
21
C
B
DC 202 212 400 441 841 29см
BC 292 212 841 441 400 20см
1
1
2
1) Найдем SADC S ADC АD АC 20 21 210см
2
2
2) Найдем SADB
3) Найдем SCDB
Sбок = SADC+ SADB + SCDB
1
1
S ADB АD АB 20 29 290см 2
2
2
1
1
SСDB DC BC 29 20 290см 2
2
2
4) Найдем площадь боковой поверхности пирамиды
Sбок = SADC+ SADB + SCDB = 210 + 290 + 290 = 790 см 2

16.

Задача №2. В правильной четырёхугольной пирамиде сторона основания равна 6
см, а угол наклона боковой грани к плоскости основания равен 60 градусам.
Найдите боковое ребро пирамиды.
Найти: МС – ?
Решение: 1) Т.к. дана прав. четырёхугол. пирамида, то в
основании лежит квадрат со стороной 6 см.
?
2) Угол MKO = 60 и треугольник MOK –прямоугольный
cos 600
6
60
B
O
A
6
C
3
3 K
3
D
MK
3
6см
0
cos 60
3) Рассмотрим треугольник МСK – прямоугольный:
K
6
OK
MK
по т. Пифагора найдем МС
МС 2 МK 2 KС 2
МС 2 6 2 32
МС 36 9 45 3 5см