Similar presentations:
Пирамида. Правильная пирамида
1. Пирамида
Правильная пирамида2.
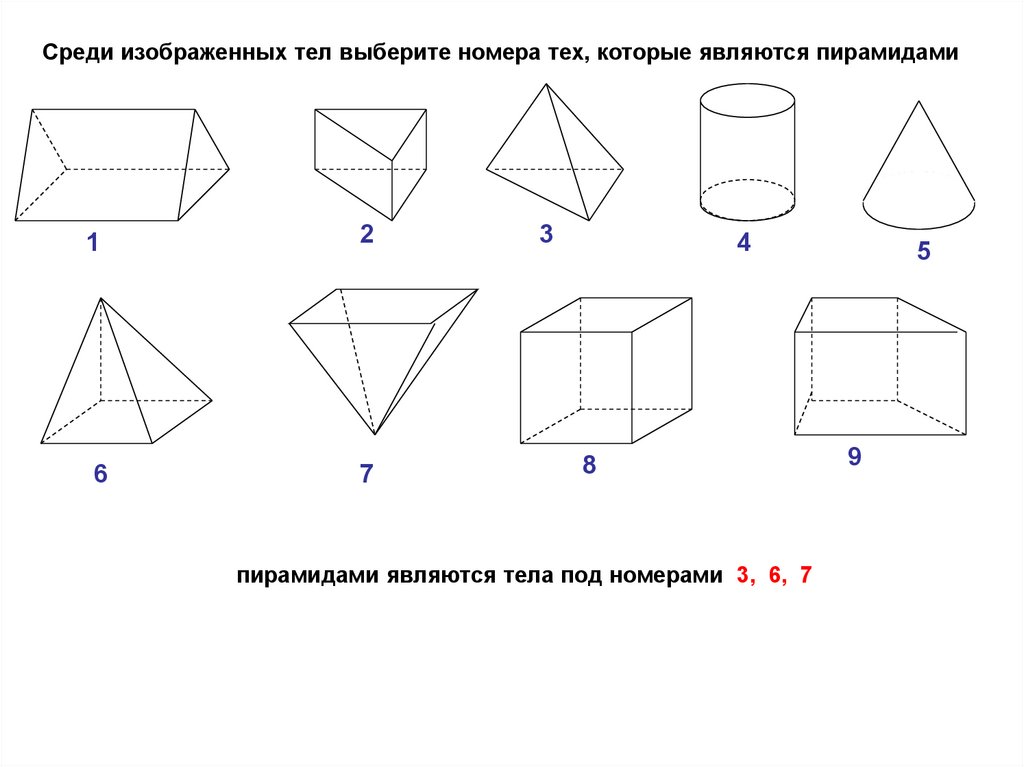
Среди изображенных тел выберите номера тех, которые являются пирамидами1
6
2
7
3
4
8
пирамидами являются тела под номерами 3, 6, 7
5
9
3.
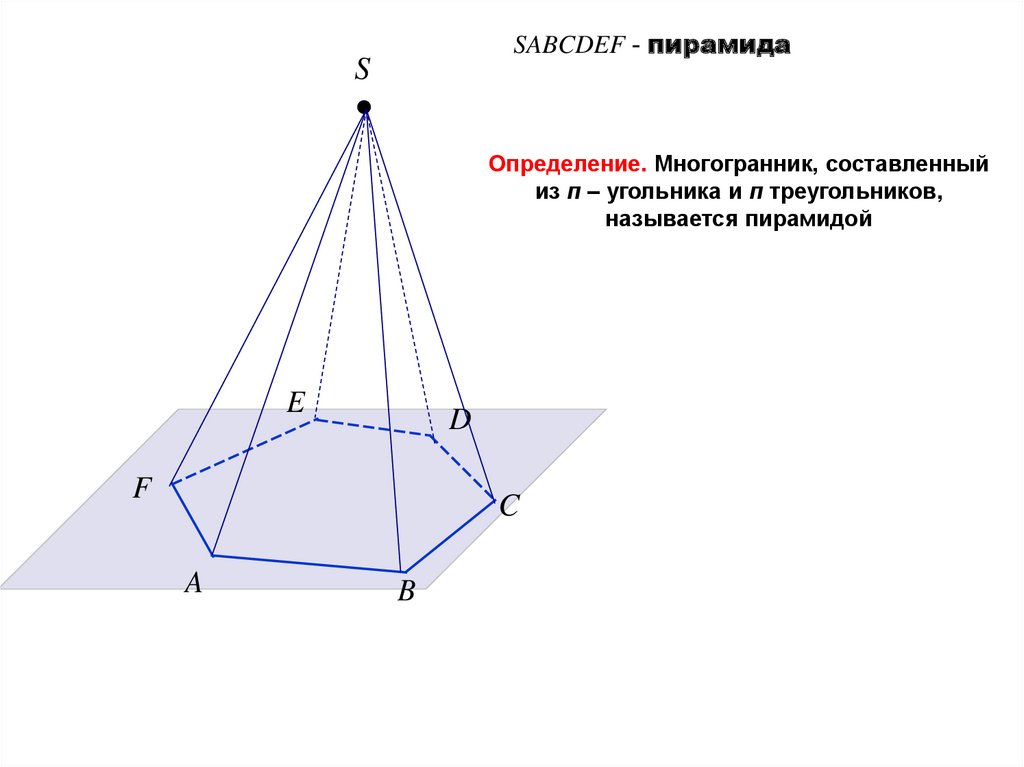
SABCDEF - пирамидаS
Определение. Многогранник, составленный
из п – угольника и п треугольников,
называется пирамидой
E
D
F
C
A
B
4.
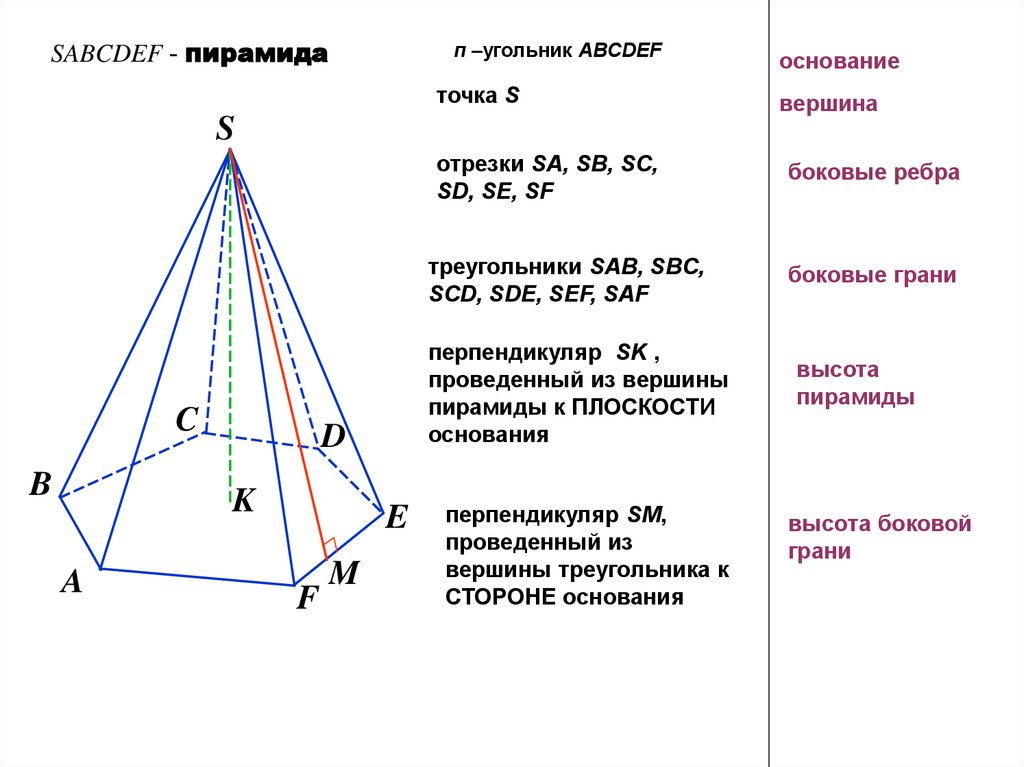
SABCDEF - пирамидап –угольник ABCDEF
точка S
S
отрезки SA, SB, SC,
SD, SE, SF
треугольники SAB, SBC,
SCD, SDE, SEF, SAF
C
B
D
K
A
перпендикуляр SK ,
проведенный из вершины
пирамиды к ПЛОСКОСТИ
основания
E
F
M
перпендикуляр SM,
проведенный из
вершины треугольника к
СТОРОНЕ основания
основание
вершина
боковые ребра
боковые грани
высота
пирамиды
высота боковой
грани
5. Правильная пирамида
Определение. Пирамида называется правильной, если еёоснованием является правильный многоугольник, а вершина
проецируется в центр основания.
Центром правильного
многоугольника
называется центр
вписанной в него ( или
описанной около него)
окружности
Все боковые рёбра
правильной
пирамиды равны, а
боковые грани
являются
равнобедренными
треугольниками
О
О
О
О
О
О
6. Апофема правильной пирамиды
Апофема - это высотабоковой грани
правильной пирамиды,
проведенная из вершины пирамиды к стороне основания
МН – апофема правильной
пирамиды
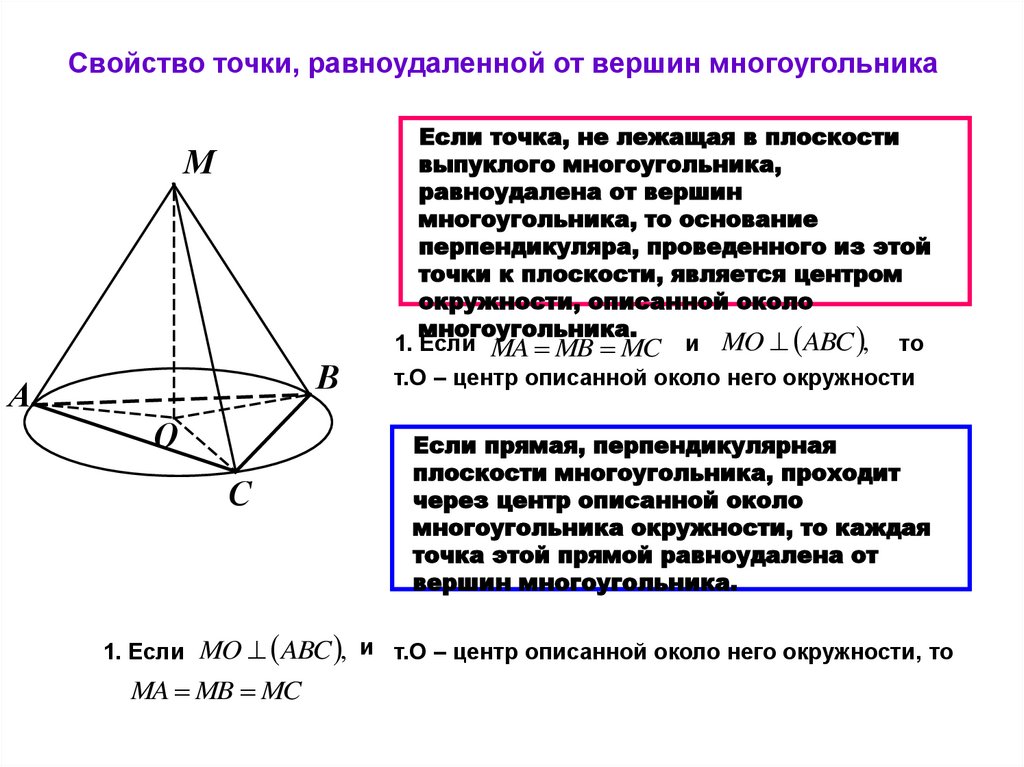
7. Свойство точки, равноудаленной от вершин многоугольника
Если точка, не лежащая в плоскостивыпуклого многоугольника,
равноудалена от вершин
многоугольника, то основание
перпендикуляра, проведенного из этой
точки к плоскости, является центром
окружности, описанной около
многоугольника.
1. Если MA MB MC и MO ABC , то
М
В
А
т.О – центр описанной около него окружности
О
Если прямая, перпендикулярная
плоскости многоугольника, проходит
через центр описанной около
многоугольника окружности, то каждая
точка этой прямой равноудалена от
вершин многоугольника.
С
MA MB MC
и
1. Если MO ABC ,
т.О – центр описанной около него окружности, то
8.
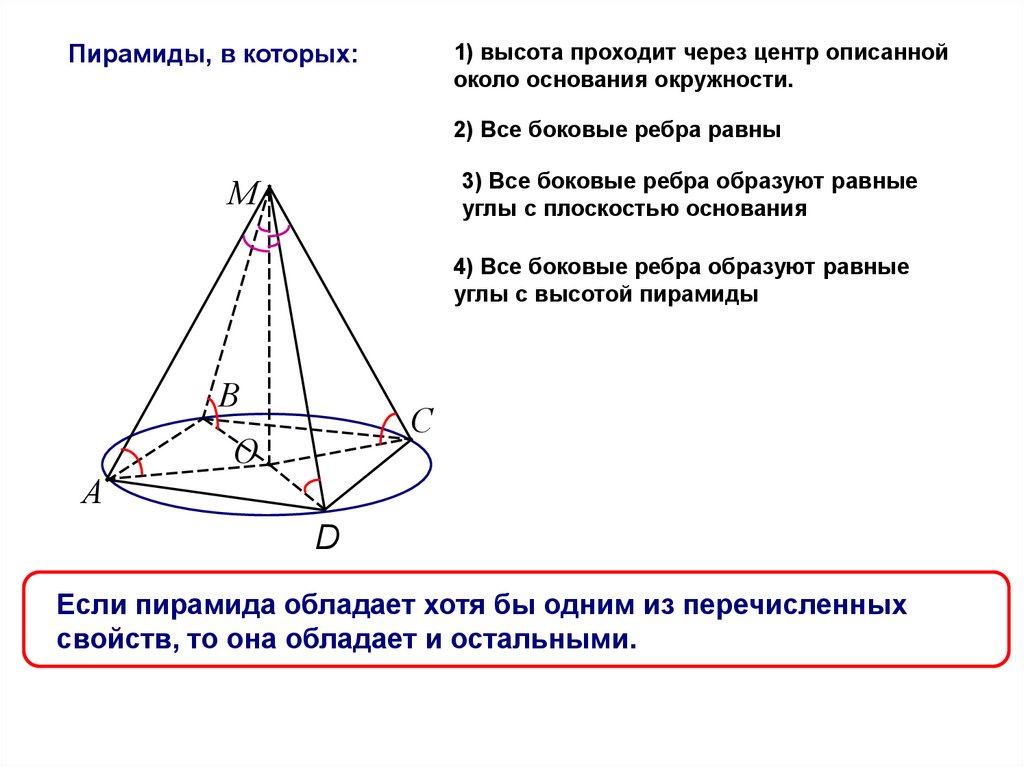
1) высота проходит через центр описаннойоколо основания окружности.
Пирамиды, в которых:
2) Все боковые ребра равны
3) Все боковые ребра образуют равные
углы с плоскостью основания
М
4) Все боковые ребра образуют равные
углы с высотой пирамиды
В
С
О
А
D
Если пирамида обладает хотя бы одним из перечисленных
свойств, то она обладает и остальными.
9. Свойство точки, равноудаленной от сторон многоугольника
Если точка, не лежащая в плоскостивыпуклого многоугольника, равноудалена
от сторон многоугольника, то основание
перпендикуляра, проведенного из этой
точки к плоскости, является центром
окружности, вписанной в многоугольник.
S
B
N
A
O
K
M
C
Если прямая, перпендикулярная плоскости
многоугольника, проходит через центр
вписанной в многоугольник окружности, то
каждая точка этой прямой равноудалена от
сторон многоугольника.
10.
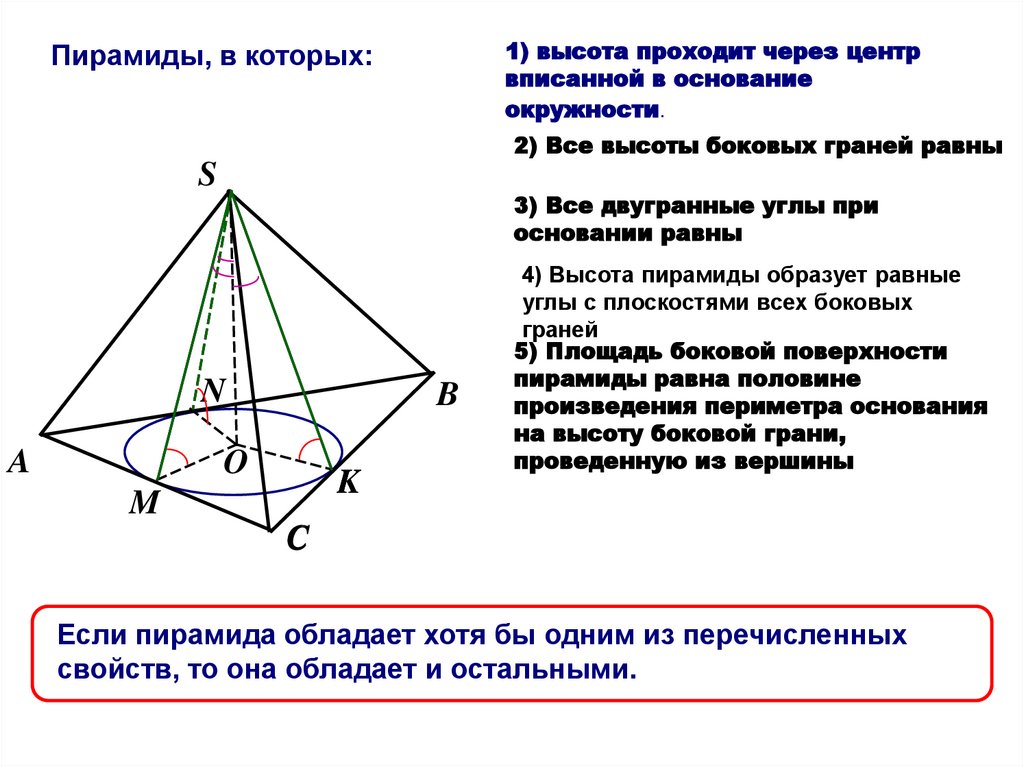
1) высота проходит через центрвписанной в основание
окружности.
Пирамиды, в которых:
2) Все высоты боковых граней равны
S
3) Все двугранные углы при
основании равны
N
A
B
O
K
M
4) Высота пирамиды образует равные
углы с плоскостями всех боковых
граней
5) Площадь боковой поверхности
пирамиды равна половине
произведения периметра основания
на высоту боковой грани,
проведенную из вершины
C
Если пирамида обладает хотя бы одним из перечисленных
свойств, то она обладает и остальными.
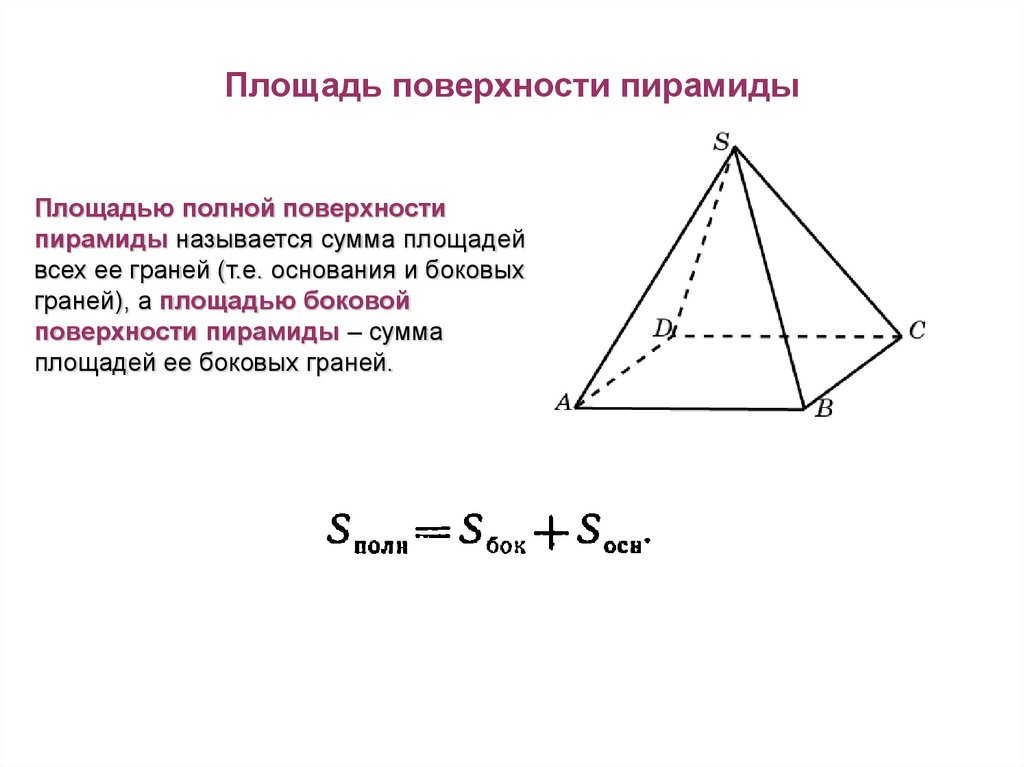
11. Площадь поверхности пирамиды
Площадью полной поверхностипирамиды называется сумма площадей
всех ее граней (т.е. основания и боковых
граней), а площадью боковой
поверхности пирамиды – сумма
площадей ее боковых граней.
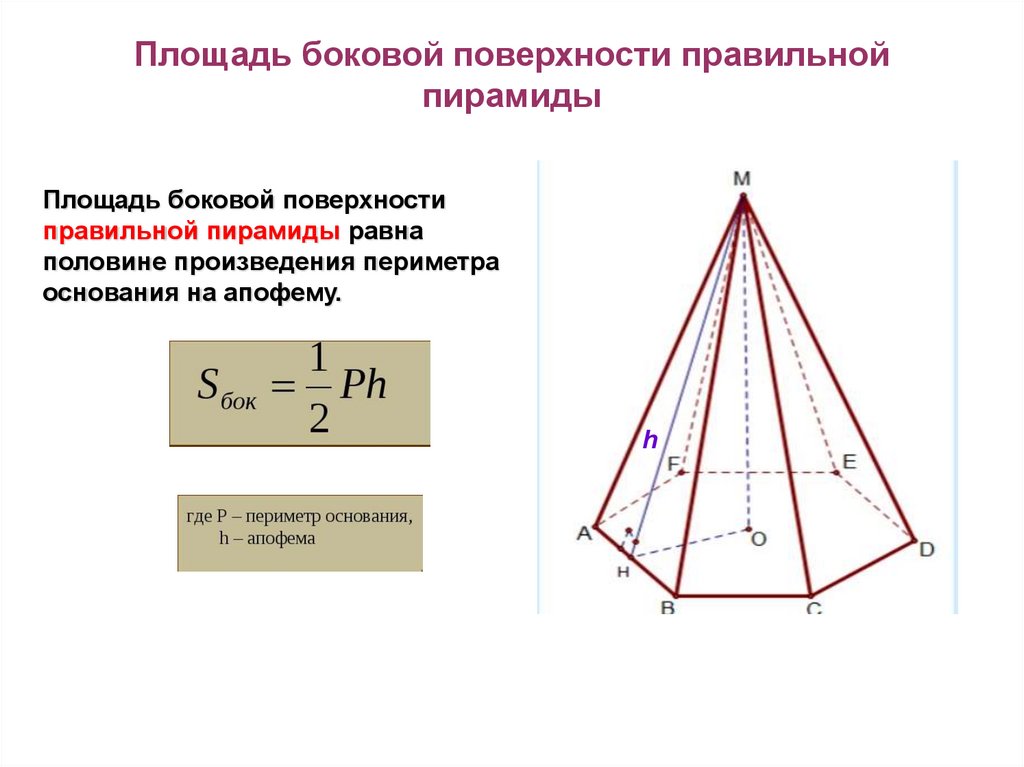
12. Площадь боковой поверхности правильной пирамиды
Площадь боковой поверхностиправильной пирамиды равна
половине произведения периметра
основания на апофему.
h
13.
Для правильных п – угольников:a
R
1800
2 sin
n
r
a
180 0
2tg
n
R - радиус описанной около п – угольника окружности
r - радиус вписанной в п – угольник окружности
а – сторона основания правильного п – угольника
п – количество строн правильного п – угольника
14.
Задача 1. В правильной треугольной пирамиде сторона основания равна 6 , авысота пирамиды равна 8 . Найти а) боковое ребро пирамиды; б) площадь боковой
поверхности пирамиды.
М
Дано: МАВС – правильная пирамида, МО = 8 , АВ = 6 ,
Найти: а) МС , б) Sáîę
Решение:
А
С
О
Н
В
S PABC MH
1. Так как пирамида правильная по условию, то АВ = ВС = АС = 6
PABC 3 6 18
2. Для нахождения длины бокового ребра проведем отрезок ОС ( радиус
описанной около треугольника АВС окружности) и рассмотрим
треугольник МОС.
MO ABC , OC ABC MO OC MOC прямоугольный
OC R
3. Найдем ОС.
AB
6
6
6
2 3
0
0
180 2 sin 60
3
3
2
2 sin
2
3
4. В треугольнике МОС по т. Пифагора найдем МС
MC MO 2 CO 2 82 2 3
2
64 12 76 2 19
15.
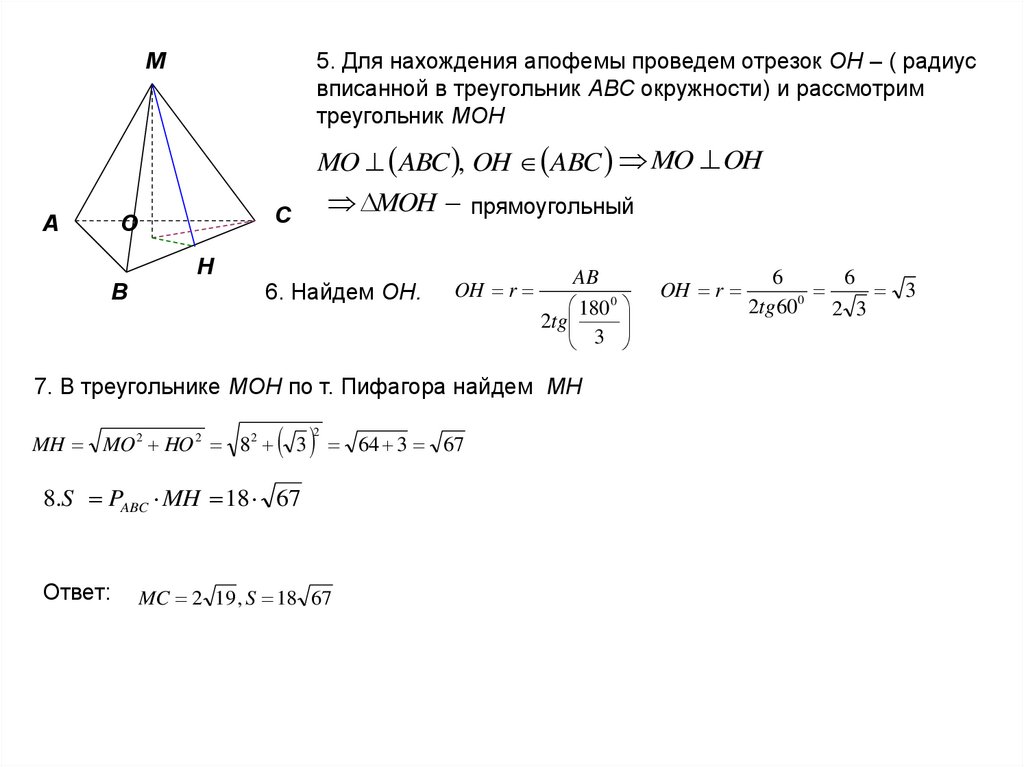
М5. Для нахождения апофемы проведем отрезок ОН – ( радиус
вписанной в треугольник АВС окружности) и рассмотрим
треугольник МОН
MO ABC , OH ABC MO OH
А
MOH прямоугольный
С
О
Н
В
6. Найдем ОН.
OH r
AB
1800
2tg
3
7. В треугольнике МОН по т. Пифагора найдем МН
MH MO 2 HO 2 82
3
2
64 3 67
8.S PABC MH 18 67
Ответ:
MC 2 19 , S 18 67
OH r
6
6
3
0
2tg 60
2 3






 mathematics
mathematics








