Дискретная модель импульсной САР. Дискретная модель цифровой САР. Лекция 15

1.

РАДИОАВТОМАТИКА
Лекция 15
ДИСКРЕТНАЯ МОДЕЛЬ
ИМПУЛЬСНОЙ САР.
ДИСКРЕТНАЯ МОДЕЛЬ
ЦИФРОВОЙ САР

2. ДИСКРЕТНАЯ МОДЕЛЬ ИМПУЛЬСНОЙ СИСТЕМЫ

x(t)
u(t)
ИЭ
Для АИМ второго рода:
v(t)
НЧ
y(t)
v(t) = u(nT)·S(t – nT),
где S(t) – форма импульса.
n
Импульсный элемент заменяется на последовательное соединение идеального
δ-импульсного элемента и формирующего фильтра c передаточной функцией
Kфф(p) =
S(t)e-ptdt.
0
x(t)
u(t)
v*(t)
ФФ
v(t)
НЧ
y(t)
v*(t)
=
u(nT)·δ(t – nT).
n
Формирующий фильтр и непрерывная часть объединяются в приведенную непрерывную
часть с передаточной функцией Kпнч(p) = Kфф(p) Kнч(p).

3.

x(t)
v*(t)
u(t)
Kпнч(p)
y(t)
Перейдем к нормированному времени t = t/T.
С изменением временного масштаба изменится и передаточная функция ПНЧ
q
1
Kпнч(p = ), где q = pT.
T
T
Составим дискретную модель импульсной системы, заменяя δ-импульсный элемент
ключом, импульсный процесс v*(t) – решетчатой функцией v[n], а непрерывные
процессы – смещенными решетчатыми функциями.
Kпнч(q) =
u[n,ε]
x[n,ε]
v[n]
Kпнч(z,ε)
y[n,ε]
Дискретная передаточная функция ПНЧ
Kпнч(z,ε) = Z{Kпнч(q) } находится по
таблицам Z-преобразования.
По умолчанию считается, что ключ вырезает из входного процесса u[n,ε] значения
слева от момента дискретизации.
v[n] = u[n-1,1].
u
u[n]
u[n-1,1]
n–1
n
n+1
t
Модель, более удобная для анализа, получится, если
перенести ключ через вычитающее устройство.

4.

x[n-1,1]
u[n-1,1]
Kпнч(z,ε)
y[n,ε]
y[n-1,1]
Найдем передаточную функцию замкнутой системы как отношение
Z-преобразований выходного и входного процессов
Z{y[n,ε]}
Y(z,ε)
Kз(z,ε) =
= -1
.
Z{u[n-1,1]} z U(z,1)
Y(z,ε) = Z{u[n-1,1]}Kпнч(z,ε) = z-1U(z,1) Kпнч(z,ε) = z-1(X(z,1) -Y(z,1)) Kпнч(z,ε).
Примем ε = 1
z-1X(z,1) Kпнч(z,1)
Y(z,1) = z-1(X(z,1) -Y(z,1)) Kпнч(z,1),
Y(z,1) =
.
1 + z-1Kпнч(z,1)
Y(z,ε) =
z-1(X(z,1)
z-1X(z,1) Kпнч(z,ε)
z-1X(z,1) Kпнч(z,1)
) Kпнч(z,ε) =
-1
1 + z-1Kпнч(z,1)
1 + z Kпнч(z,1)
Kпнч(z,ε)
Kз(z,ε) =
.
1 + z-1Kпнч(z,1)

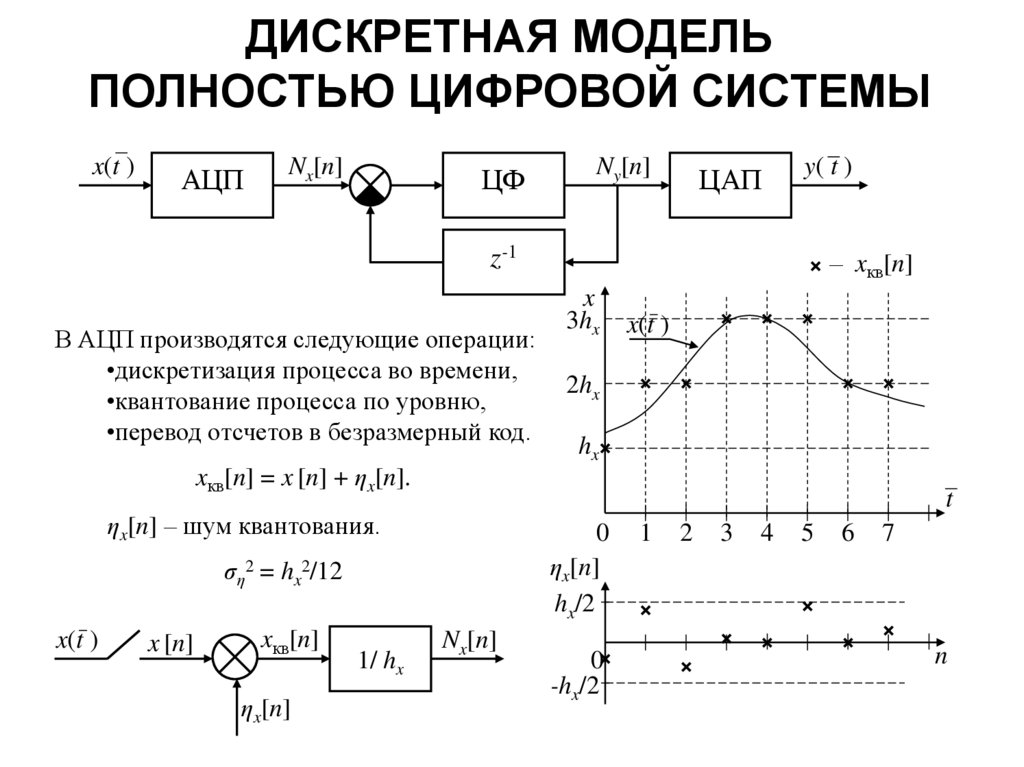
5. ДИСКРЕТНАЯ МОДЕЛЬ ПОЛНОСТЬЮ ЦИФРОВОЙ СИСТЕМЫ

x(t )
АЦП
Nx[n]
ЦФ
Ny[n]
ЦАП
y( t )
z-1
В АЦП производятся следующие операции:
•дискретизация процесса во времени,
•квантование процесса по уровню,
•перевод отсчетов в безразмерный код.
xкв[n] = x [n] + ηx[n].
xкв[n]
ηx[n]
1/ hx
x(t )
2hx
hx
0
ηx[n]
hx/2
ση2 = hx2/12
x [n]
x
3hx
t
ηx[n] – шум квантования.
x(t )
– xкв[n]
Nx[n]
0
-hx/2
1
2
3
4
5
6
7
n

6.

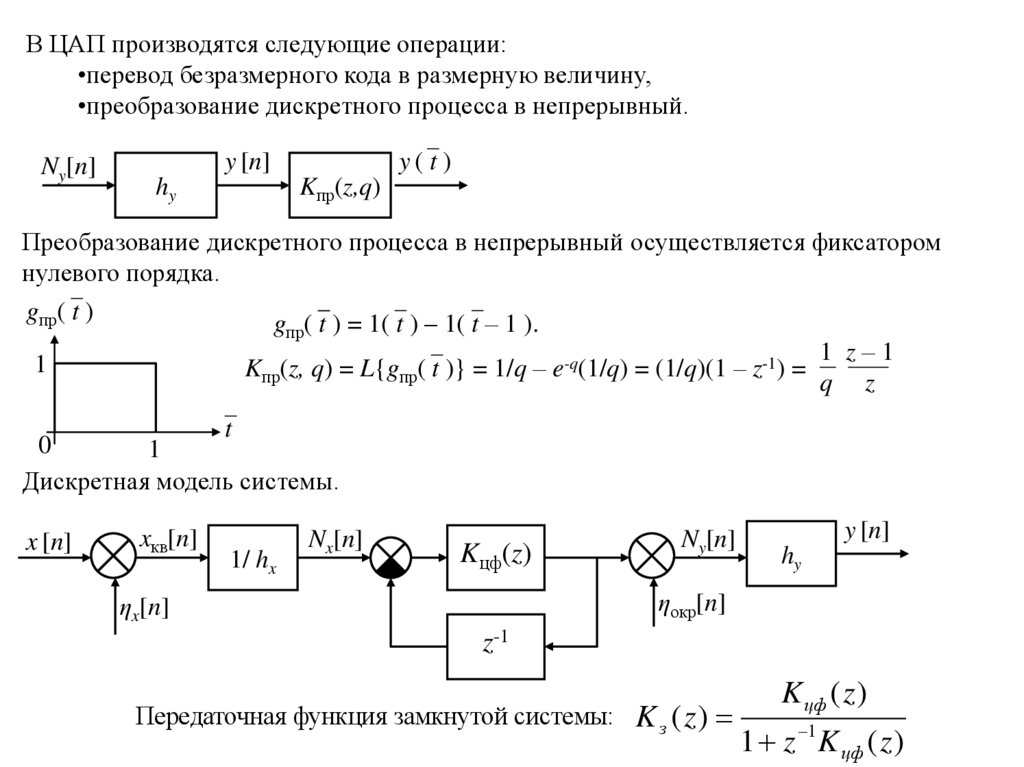
В ЦАП производятся следующие операции:
•перевод безразмерного кода в размерную величину,
•преобразование дискретного процесса в непрерывный.
Ny[n]
y [n]
hy
y( t )
Kпр(z,q)
Преобразование дискретного процесса в непрерывный осуществляется фиксатором
нулевого порядка.
gпр( t )
g ( t ) = 1( t ) – 1( t – 1 ).
пр
Kпр(z, q) = L{gпр( t )} = 1/q – e-q(1/q) = (1/q)(1 – z-1) =
1
1 z–1
q z
t
0
1
Дискретная модель системы.
x [n]
xкв[n]
1/ hx
Nx[n]
Kцф(z)
Ny[n]
y [n]
hy
ηокр[n]
ηx[n]
z-1
Передаточная функция замкнутой системы:
K з ( z)
K цф ( z )
1 z 1 K цф ( z )

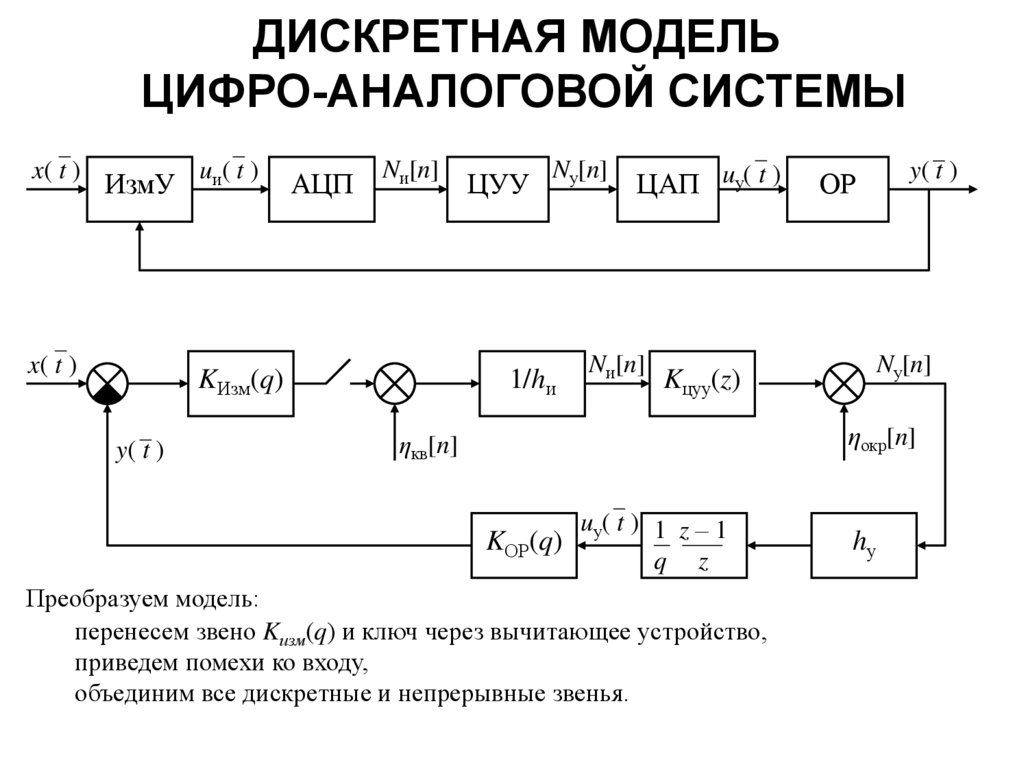
7. ДИСКРЕТНАЯ МОДЕЛЬ ЦИФРО-АНАЛОГОВОЙ СИСТЕМЫ

x( t )
ИзмУ
x( t )
uи( t )
АЦП
Nи[n]
KИзм(q)
y( t )
ЦУУ
Nу[n]
1/hи
ЦАП uу( t )
Nи[n]
ОР
y( t )
Nу[n]
Kцуу(z)
ηокр[n]
ηкв[n]
KОР(q)
uу( t ) 1 z – 1
q z
Преобразуем модель:
перенесем звено Kизм(q) и ключ через вычитающее устройство,
приведем помехи ко входу,
объединим все дискретные и непрерывные звенья.
hу

8.

x( t )
KИзм(q)
ηкв[n]
hи
Kцуу(z)
ηокр[n]
xизм [n] + η [n]
hу
z–1
Kцуу(z)
hи
z
yизм( t )
1
K (q) KИзм(q)
q ОР
Дискретная передаточная функция непрерывной части определяется как
Z-преобразование от непрерывной передаточной функции
Kнч(z,ε) = Z{Kнч(q)}.
xизм [n] + η [n]
hу
z–1
K (z) z Kнч(z, )
hи цуу
z 1
K p ( z, ) K цуу ( z )
K нч ( z, )
hи
z
hy
yизм [n, ]
K з ( z, )
K р ( z, )
1 z 1 K р ( z ,1)