Определители. Определение определителя

1.

2. Определители
2.1 определение определителя
Бывают только у квадратных матриц
Обозначение:
1 1:
2 2 :
det A A A
a a
a b
c d ad bc
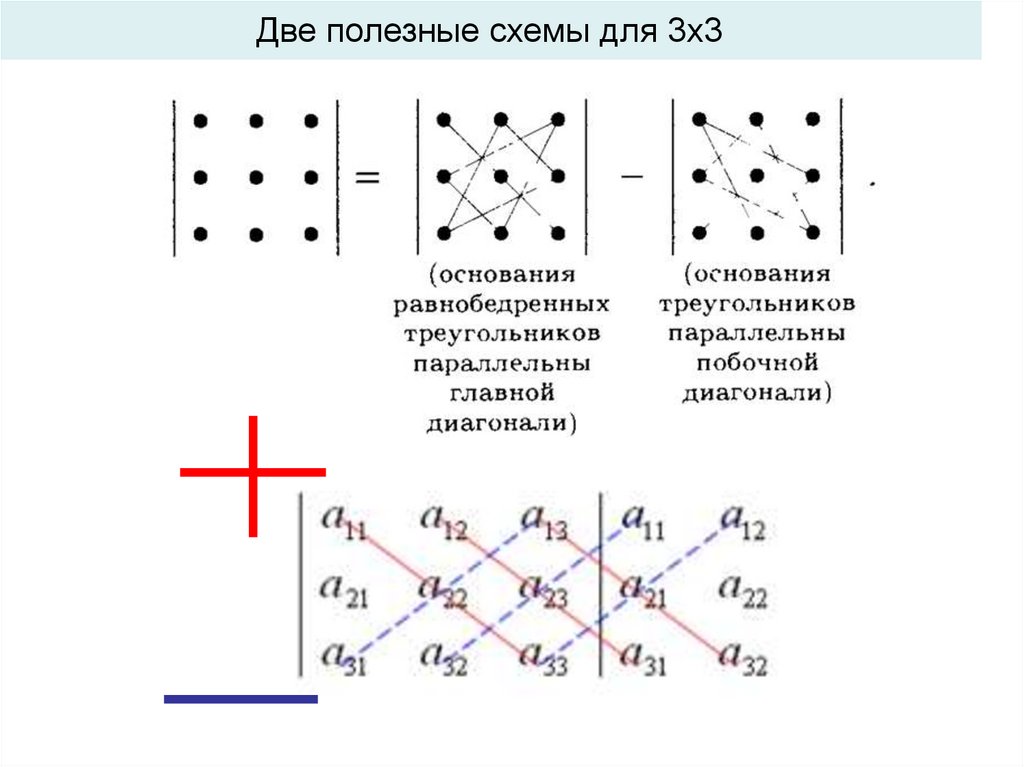
a11 a12 a13
3 3: a21 a22 a23 a11a22 a33 a12 a23 a31 a13 a21a32
a a a
a13 a22 a31 a12 a21a32 a11a23 a33
31 32 33

2.

Две полезные схемы для 3х3

3.

Миноры (без которых дальше ничего не получится)
Определение минора k-го порядка
Выберем в А произвольно k строк и k столбцов;
Элементы, стоящие на пересечении выбранных строк и столбцов составляют
квадратную матрицу М размера kxk;
Определитель этой матрицы М и есть минор k-го порядка матрицы А;
Различных миноров k-го порядка у матрицы А очень много.
С
k 2
n
штук
Миноров 3-го порядка у матрицы 4х4 всего 16.
1
0
3
0
1
0 1 2
3 1 0
8 1 0
0
1
0 0 1
M 1,4 3 3 1
0 8 1
0 1 2
M 1,1 3 1 0
8 1 0
1 0 1
M 2,4 3 3 1
0 8 1
1 0 1
M 4,3 0 0 2
3 3 0
M 1,2 , M 1,3
M 2,1 , M 2,2 , M 2,3
M 3,1 , M 3,2 , M 3,3 , M 3,4
M 4,1 , M 4,2 , M 4,4

4.

Вычисление определителя 4х4 с помощью миноров
a11
a
21
4 4 :
a31
a41
a12 a13 a14
a22 a23 a24
a M a M a M a M
a32 a33 a34 11 11 12 12 13 13 14 14
4
4
a42 a43 a44
( 1)i j a M ( 1)i j a M
ij ij
ij ij i 1
j 1
i — любая фиксированная строка матрицы А
j — любой фиксированный столбец матрицы А
1
0
3
0
1
0 0 1
1 0 1
0 1 2
1 ( 1)1 4 3 3 1 2 ( 1) 2 4 3 3 1 0 0
3 1 0
0 8 1
0 8 1
8 1 0
0
1

5.

a11 a12
a a
n n : 21 22
... ..
an1 an 2
... a1n
... a2 n
... ...
... ann
n
n
i j
i j
(
1)
a M
(
1)
a
M
j 1
ij ij
ij ij i 1
От миноров к алгебраическим дополнениям
( 1)i j M A алгебраическое дополнение a
ij
ij
ij
n
a A
ij ij
i 1
3 3:
4 4:

6.

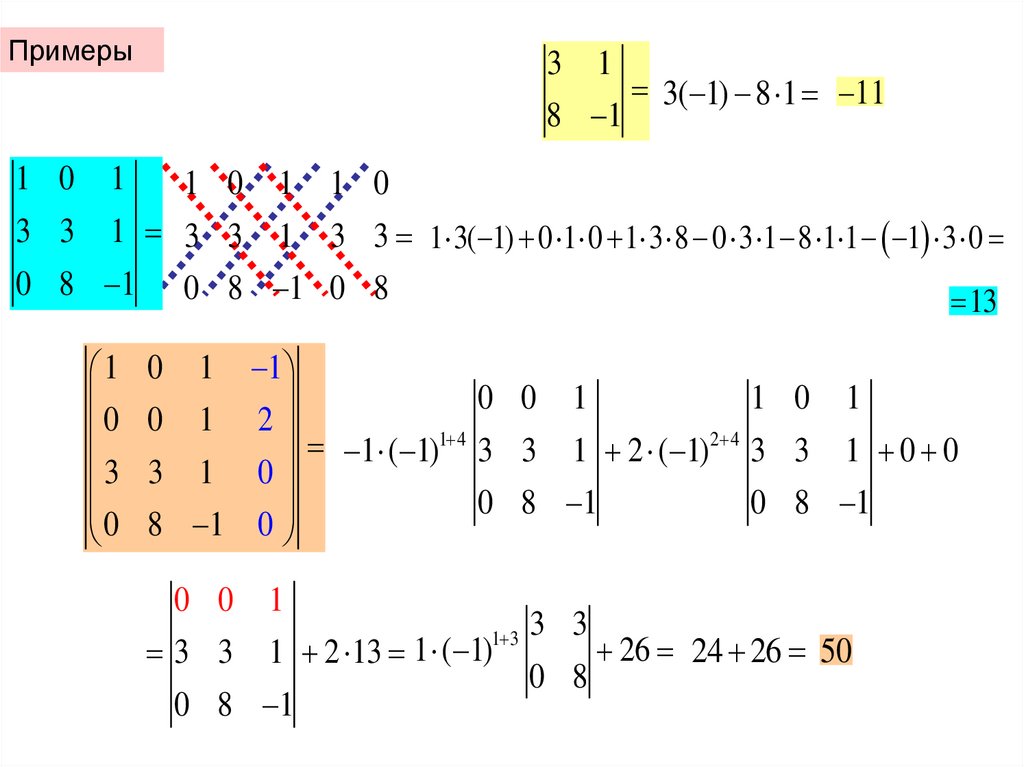
Примеры
3 1
8 1
1 0
1
1 0
1
3( 1) 8 1 11
1 0
1 3 3 1 3 3 1 3( 1) 0 1 0 1 3 8 0 3 1 8 1 1 1 3 0
0 8 1 0 8 1 0 8
13
3 3
1
0
3
0
1
0 0 1
1 0 1
0 1 2
1 ( 1)1 4 3 3 1 2 ( 1) 2 4 3 3 1 0 0
3 1 0
0 8 1
0 8 1
8 1 0
0
1
0 0
3 3
1
1 3
1 2 13 1 ( 1)
0 8 1
3 3
0 8
26 24 26 50

7.

2.2. Свойства определителей
1) det 0 0
2) det E 1
1
4) det A
det A
1
3) det A det A
T
5) det AB det A det B
6) При добавлении к любой строке (столбцу) линейной комбинации
других строк (столбцов) определитель не изменится:
ai j a j ,
где λj - некоторое число, ai , aj - строки матрицы
7) Если две строки (столбца) совпадают, то определитель равен нулю.
8) Если переставить две строки (столбца), то определитель меняет знак .
9) Если хотя бы один ряд нулевой, то определитель равен нулю.
10) Общий множитель элементов какого-либо ряда определителя можно
вынести за знак определителя.

8.

Пример использования свойств определителя
(вычисление определителя с помощью нулей)
1
0
3
0
0 1 1
0 1 2
3 1 0
8 1 0
1
1 ( 1)
4 3
0
1
0
a 3 a 4
3
0
1
0 0 1
1
0 3 2
a3 a4 0
3 1 0
a2 3a4 3
8 1 0
0
1 0 1
1
24 0 2
11 0 0
8 1 0
0
0
1 0 0
12 1
0 24 2 2 0 12 1 a a 2 0 12 1 2 1 ( 1)
11 3
3 11 0
3 11 0
3 11 3
3
1
1 1
2 (36 11) 50
Таким образом, для получения нулей в некоторой строке (столбце) можно
прибавить к ней (к нему) любые другие, умноженные на подходящие числа.

9.

Резюмируем. Способы вычисления определителей:
1. Вычисление определителя по схематическому правилу (подходит для
определителей 2-го и 3-го порядков).
2. Разложение определителя по элементам какой-либо строки или столбца
(подходит для определителей 3-го и более высоких порядков).
3. Получение нулей в какой-либо строке или столбце и разложение
определителя по этой строке или столбцу (подходит для определителей 3-го и
более высоких порядков).

10.

2.3. И снова обратная матрица
Обратная матрица — это матрица,
произведение с которой равно единице:
1
1
A A A A E
Свойства обратной матрицы
1) Обратная бывает только у квадратных:
2) Обратная к обратной равна исходной:
3) Обратная к транспонированной
равна транспонированной обратной:
1
A, A n n
A
A A
4) Обратная произведения равна произведению
обратных в обратном порядке:
5) Обратная к умноженной на число равна
обратной, разделенной на это число:
1 1
T
1
A
1 T
1 1
AB
B
A
1
1
1
A
A
1
Теорема. Для того, чтобы квадратная матрица имела обратную,
необходимо и достаточно, чтобы её определитель был отличен от нуля.
Следствие. Если обратная матрица существует, то она единственная.

11.

Вычисление обратной матрицы методом присоединённой
матрицы
a11 a12
a a
A 21 22
... ..
an1 an 2
... a1n
... a2 n
, det A 0
... ...
... ann
a11 a12
a a
С 21 22
... ..
an1 an 2
... a1n A11 A21
... a2 n A12 A22
... ... ... ..
... ann A1n A2 n
A алгебраические
ij
дополнения элементов a
ij
Заметим, что
В самом деле:
... An1 det A 0
... An 2 0 det A
... ... ...
...
... Ann 0
0
n
n
j 1
j 1
... 0
... ...
... det A
... 0
cii aij Aij aij 1 M ij det A
Осталось убедиться, что:
i j
n
n
j 1
j 1
?
cik aij Akj aij 1 M kj 0, k i
i k

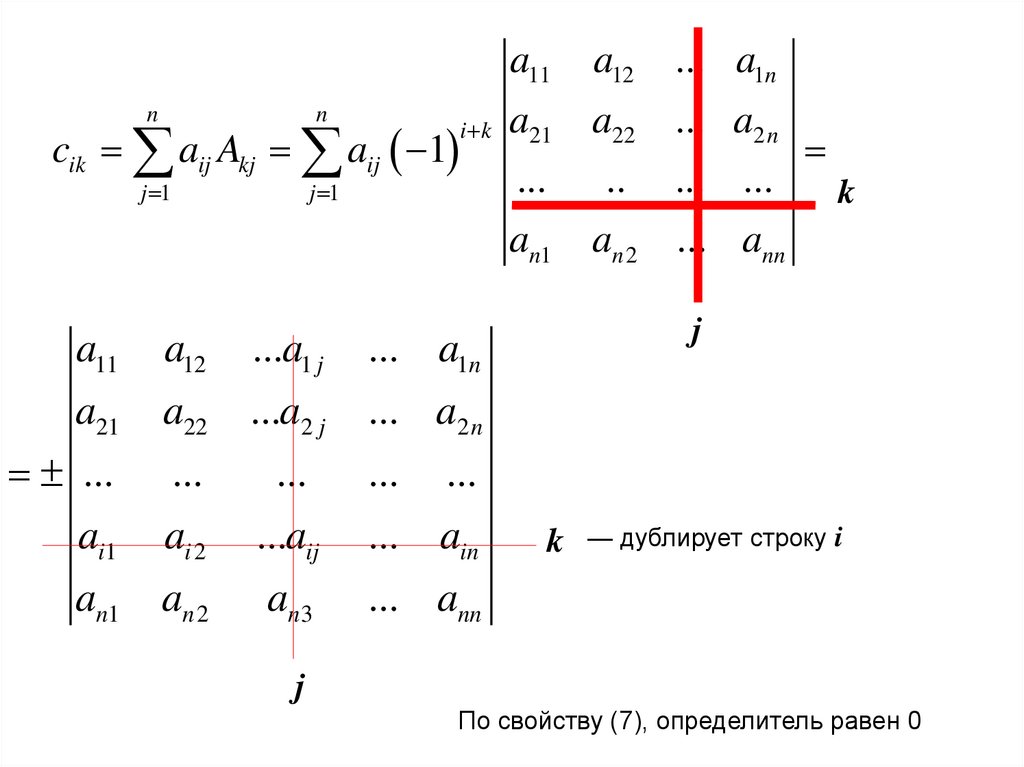
12.

n
n
j 1
j 1
cik aij Akj aij 1
i k
a11
a12
a21
a22 ... a2 n
...
an1
a11
a12
...a1 j
... a1n
a21
a22
...a2 j
... a2 n
...
...
...
ai1
ai 2
...aij
... ain
an1
an 2
an 3
... ann
...
..
... a1n
... ...
k
an 2 ... ann
j
...
k
— дублирует строку i
j
По свойству (7), определитель равен 0

13.

1
A
A
det A ij
1
Итак,
T
A
ij
где
i 1,n
j 1,n
T
- присоединенная (союзная)
матрица, или транспонированная
матрица алгебраических
дополнений
AÏ
Простой пример:
1
1
1
2 3 ?
3
Aij
1
3
AÏ
2
2
1
1
1
A11 1 ( 3) 3, A12 1 2 2,
1 1
1 2
A21 1 1 1,
2 1
1 1
det A
5
2 3
A22 1 1 1
2 2
3 1
5 5 0,6 0,2
1
A
2
1
0,4
0,2
5 5

14.

Вычисление обратной матрицы методом элементарных
преобразований
Теорема. Пусть последовательность элементарных преобразований
только над строками (столбцами) невырожденной матрицы A приводит
её к единичной матрице E. Тогда те же элементарные преобразования
приводят единичную матрицу E к обратной матрице A-1.
Элементарные преобразования:
1. Любая перестановка строк (столбцов).
2. Умножение строки (столбца) на число, отличное от нуля.
3. Прибавление к какой-либо строке (столбцу) другой строки
(столбца), умноженной на любое число.
Правило вычисления обратной матрицы:
1. Записать рядом две матрицы: A|E.
2. Получить нижний треугольник нулей матрицы А (выполнить прямой ход).
3. Получить верхний треугольник нулей матрицы А (выполнить обратный
ход).
4. Получить в главной диагонали преобразуемой матрицы единицы. Тогда на
месте исходной единичной матрицы Е будет находиться обратная
матрица А-1.

15.

Пример
3 4
A
2
3
det A 9 8 1 0
3 4 1 0
2 3 0 1
[a1 a2 ]
1 1 1 1
0 1 2 3
1 1 1 1
2 3 0 1
[a1 a2 ]
обратная матрица существует
[ 2a1 a2 ]
1 0 3 4
0 1 2 3
3 4
A
2
3
1

16.

Ещё пример
1 1
A
det A 3 2 5 0 обратная матрица существует
2 3
1 1 1 0
2 3 0 1
[a 2 a1 ]
5 0 3 1
0 5 2 1
1 0 1 1
2 5 0 1
[ a 1 / 5, a 2 /( 5)]
[5a 1 2a 2 ]
1 0 0, 6 0, 2
0 1 0, 4 0, 2
0, 6 0, 2
A
0,
4
0,
2
1