Площадь криволинейной трапеции

1.

Площадь
криволинейной
трапеции
четверг, 3 декабря 2020 г.

2.

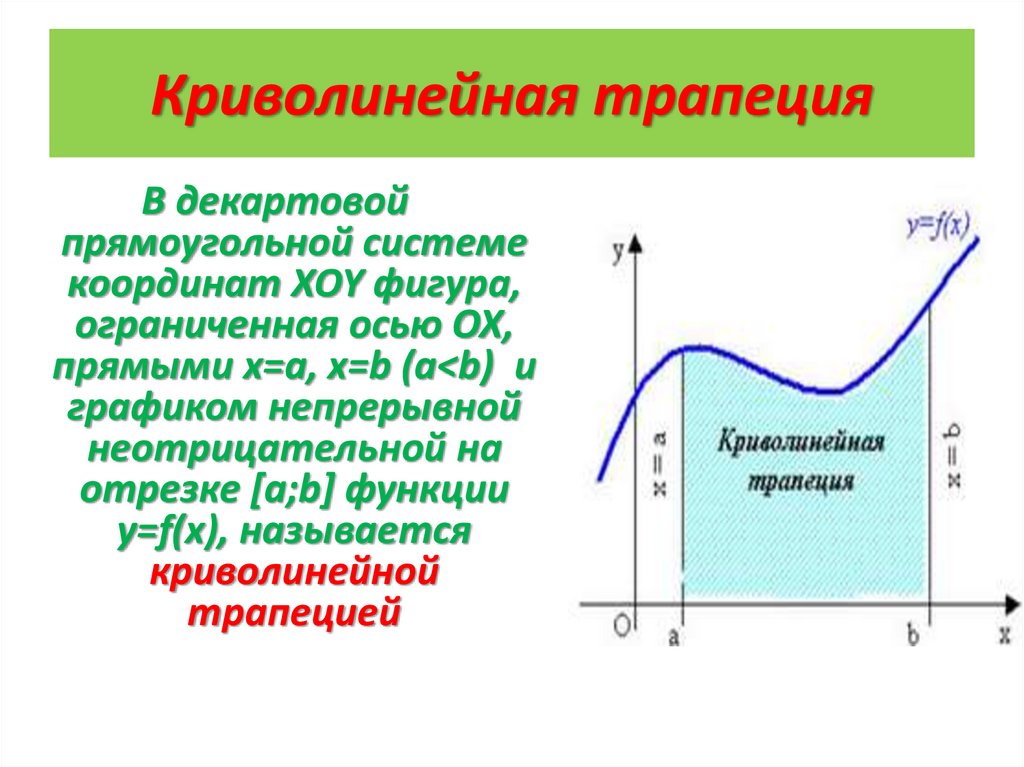
Криволинейная трапеция
В декартовой
прямоугольной системе
координат XOY фигура,
ограниченная осью OX,
прямыми x=a, x=b (a<b) и
графиком непрерывной
неотрицательной на
отрезке [a;b] функции
y=f(x), называется
криволинейной
трапецией

3.

Для вычисления площади этой фигуры
применяется следующая теорема
Теорема: Если функция f(x) непрерывна и не
отрицательна на а ; в , то справедлива
формула
b
S f x dx F x a F b F a
b
a
Формула Ньютона-Лейбница
В честь английского физика Исаака Ньютона и
немецкого философа Готфрида Лейбница.
Получивших ее независимо друг от друга и практически
одновременно

4.

b
f ( x)dx
а
Называется определенным интегралом
Числа а и в пределами интегрирования.
(нижний, в – верхний)

5.

Геометрический смысл
определенного интеграла
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
положительной на промежутке [a;b]
функции f(x), осью x и прямыми x=a и x=b:
b
S f ( x )dx
a

6.

Площадь криволинейной трапеции,
ограниченной графиком непрерывной
отрицательной на промежутке [a;b]
функции f(x), осью x и прямыми x=a и x=b:
b
S f ( x)dx
a

7.

Замечание: Если функция изменяет знак на
промежутке [a;b] , то
b
S S1 S 2 f ( x)dx
a

8.

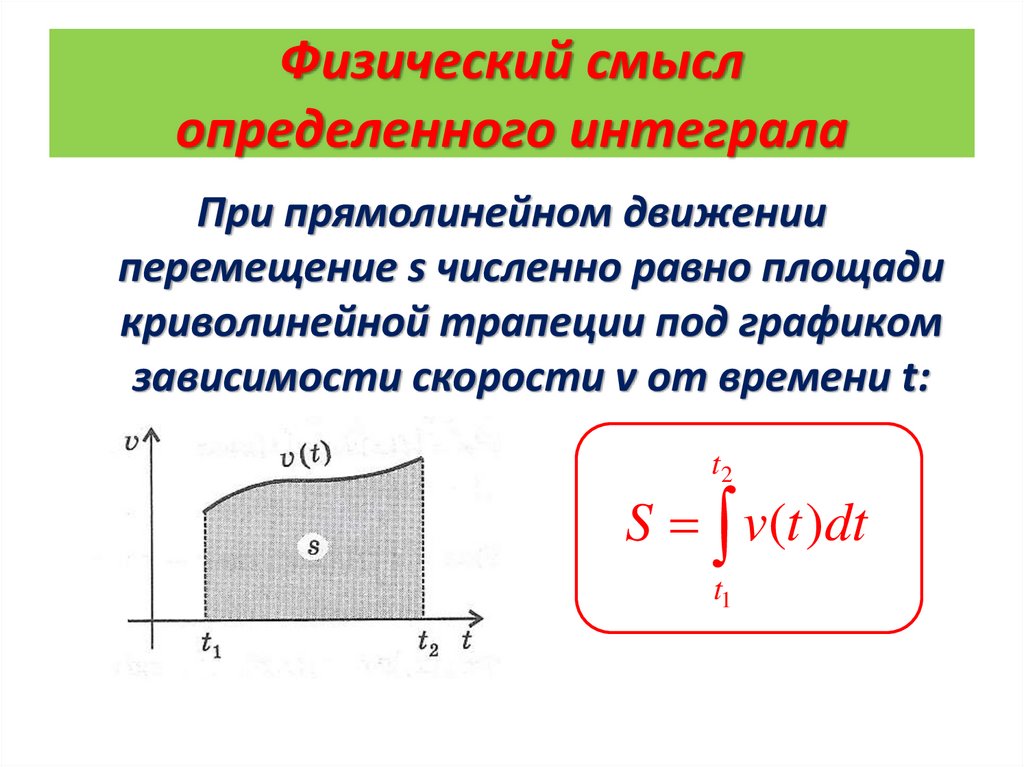
Физический смысл
определенного интеграла
При прямолинейном движении
перемещение s численно равно площади
криволинейной трапеции под графиком
зависимости скорости v от времени t:
t2
S v(t )dt
t1

9.

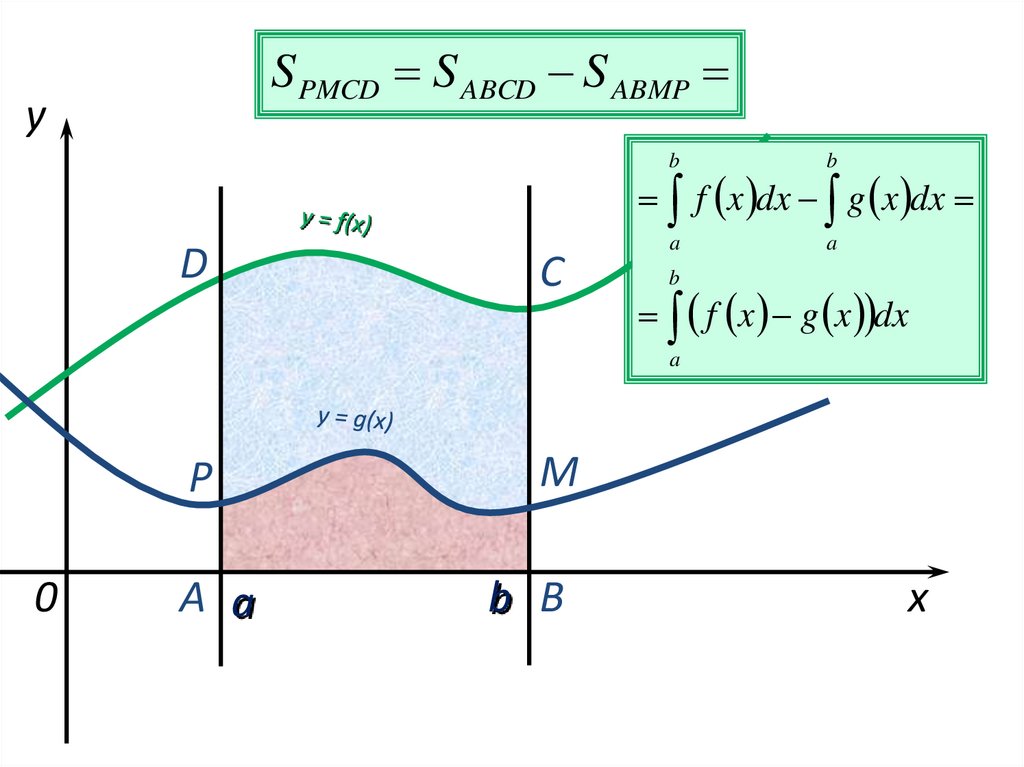
S PMCD S ABCD S ABMP
y
b
b
a
a
f x dx g x dx
D
C
b
f x g x dx
a
P
0
A a
M
b B
x

10.

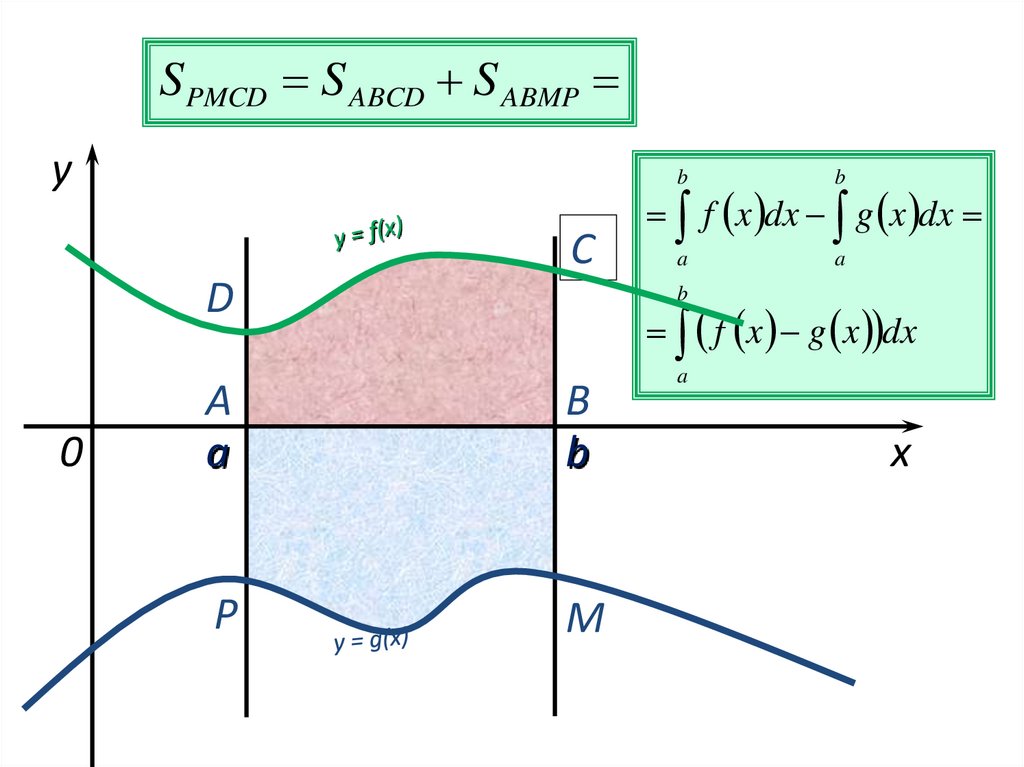
S PMCD S ABCD S ABMP
y
C
D
0
b
b
a
a
f x dx g x dx
b
f x g x dx
A
a
B
b
P
M
a
x

11.

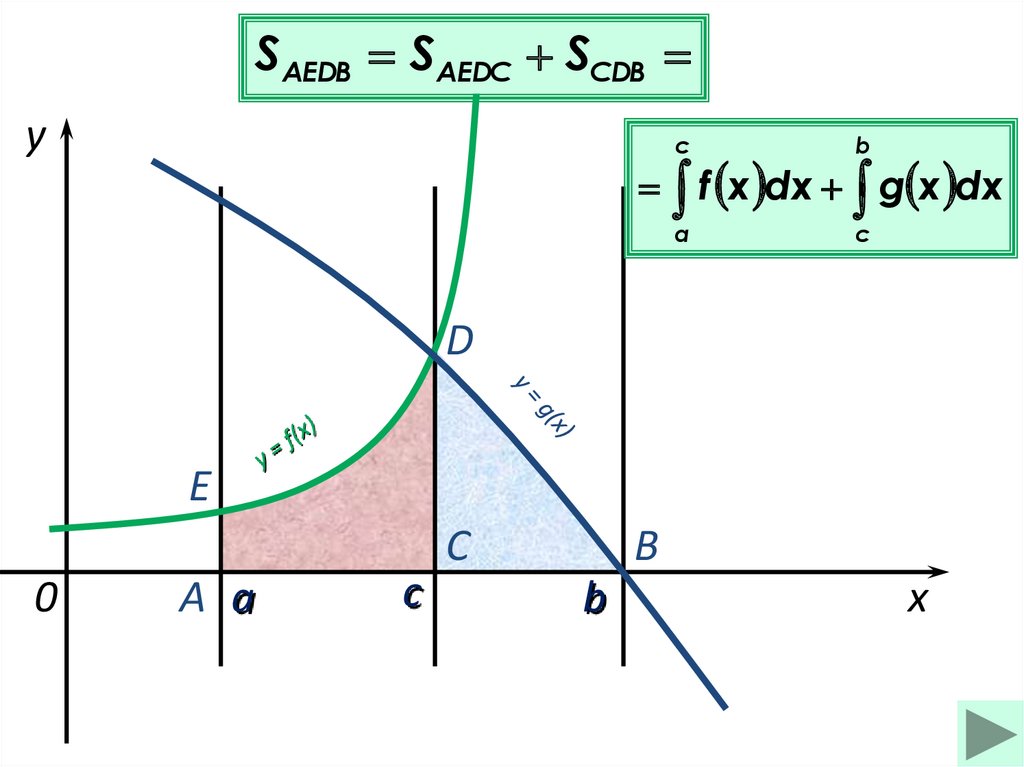
SАЕDВ SAEDC SСDB
y
с
b
a
с
f x dx g x dx
D
Е
C
0
A a
с
B
b
x

12.

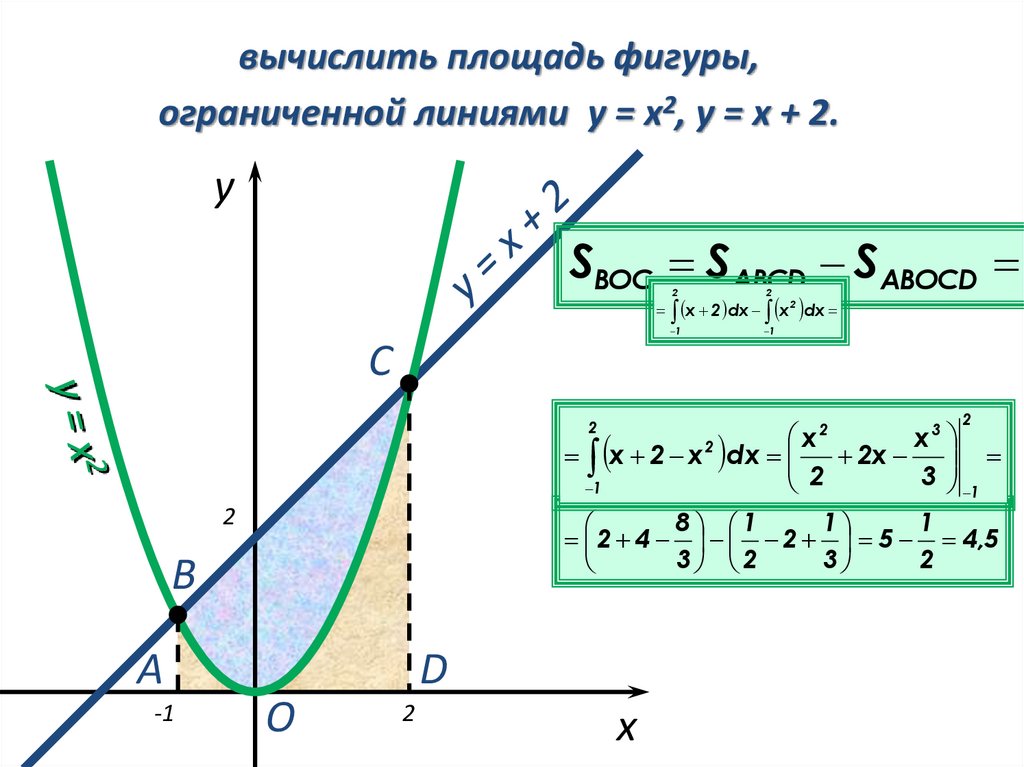
вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
2
2
1
1
2
x 2 dx x dx
C
2
2
B
A
-1
2
x
x
х 2 х 2 dx 2x
3 1
2
1
8 1
1
1
2 4 2 5 4,5
3 2
3
2
D
O
2
x
2
3

13.

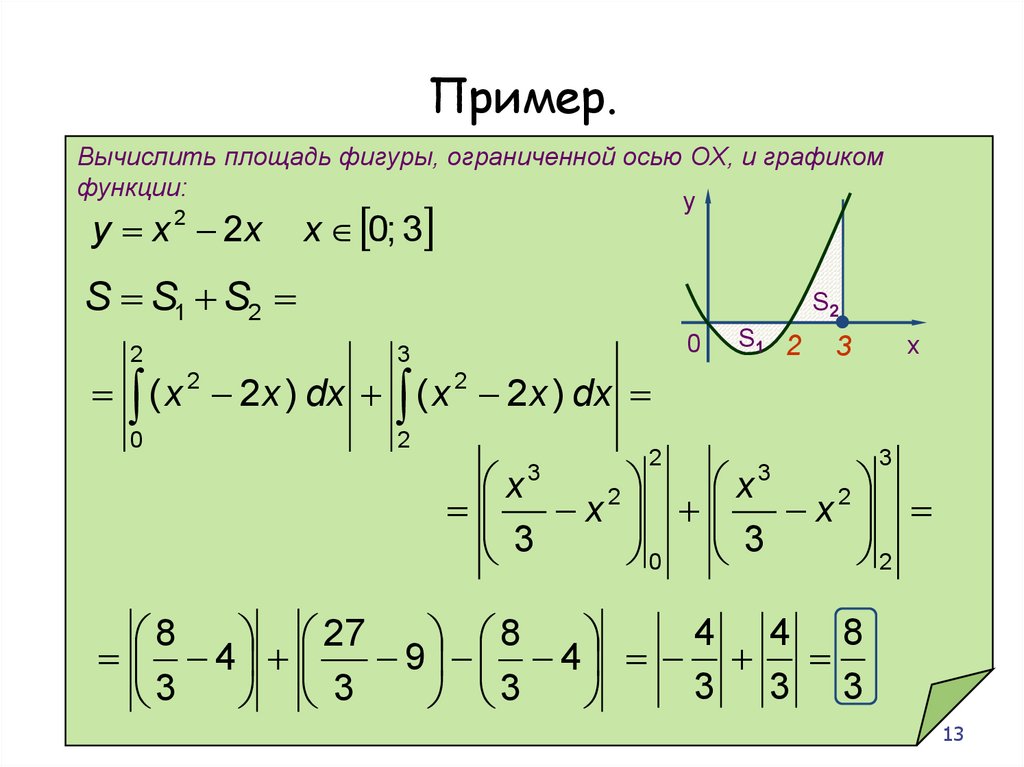
Пример.
Вычислить площадь фигуры, ограниченной осью OX, и графиком
функции:
y
y x 2 2x
x 0; 3
S S1 S2
S2
2
3
0
2
0
S1 2
3
x
( x 2 2 x ) dx ( x 2 2 x ) dx
2
3
x
x
2
2
x
x
3
0 3
2
3
3
4 4 8
8
27
8
4
9 4
3 3 3
3
3
3
13

14.

Вычисление объема тела вращения
Пусть вокруг оси OX вращается криволинейная трапеция,
ограниченная непрерывной линией y = f(x) > 0, отрезком [a; b] и
прямыми x = a, x = b.
. при вращении фигура
Полученная
y
называется телом вращения.
Объем полученного тела
вычисляется по формуле:
b
0
а
b
x
Vx y 2dx
a
Если криволинейная трапеция, ограниченная
графиком функции x = q(y) > 0, прямыми y = c,
y = d и осью OY, то объем тела, образованного
вращением этой фигуры вокруг оси OY равен:
d
Vy x 2dy
c
14

15.

Пример.
Вычислить объем тела, образованного вращением
фигуры, ограниченной линиями:
y x 2;
x 0;
y 4
вокруг оси OY.
y
4
4
0
0
2
0
4
Vy y dy ydy
2
x
y
2
4
8
0
15