Площадь криволинейной трапеции

1. Площадь криволинейной трапеции

ГБОУ РОЦ №76
Носкова А.Ю.

2. Содержание

Площадь криволинейной трапеции
Площадь криволинейной трапеции (1)
Площадь криволинейной трапеции (2)
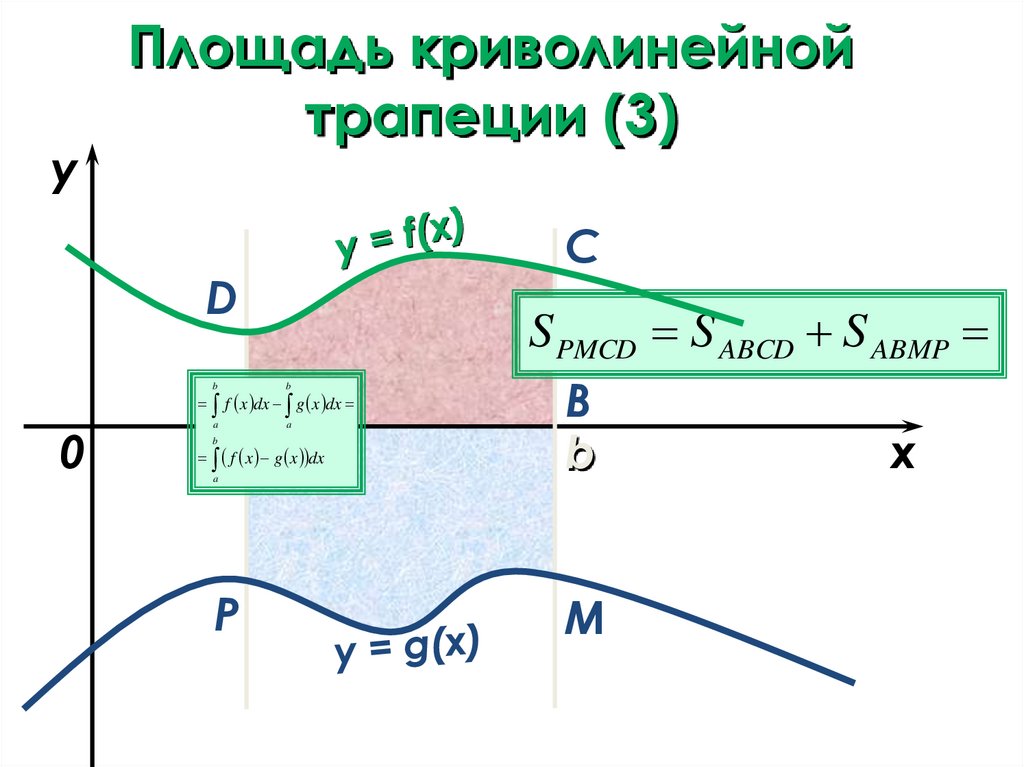
Площадь криволинейной трапеции (3)
Площадь криволинейной трапеции (4)
Пример (1)
Пример (2)

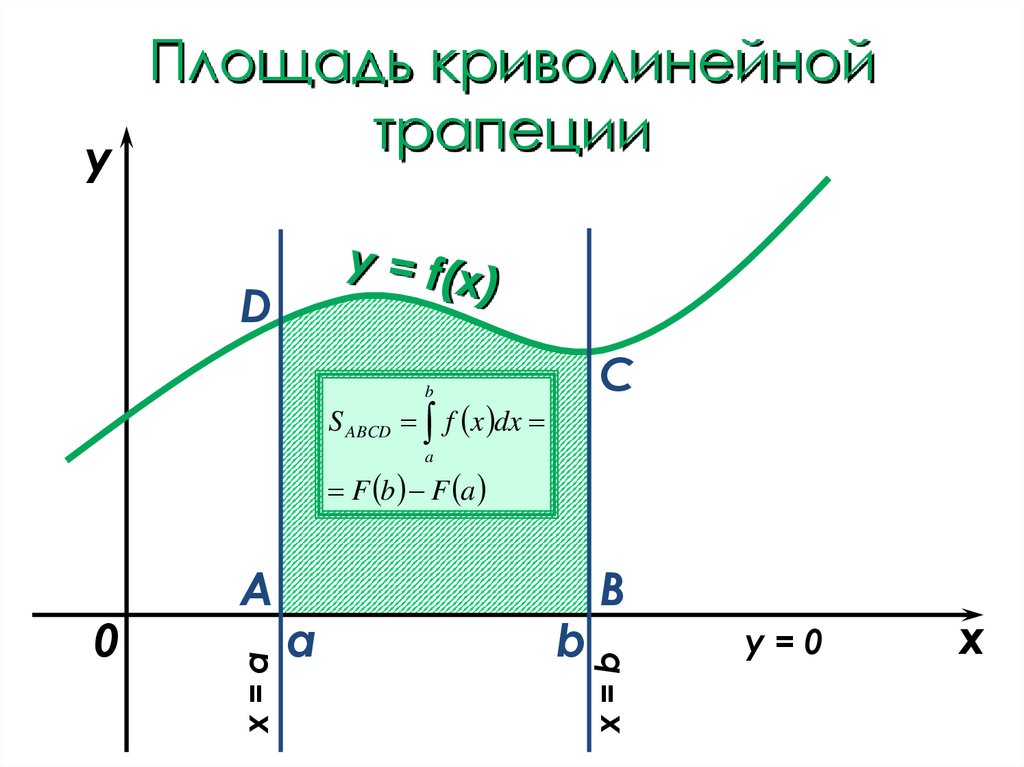
3. Площадь криволинейной трапеции

y
D
C
b
S ABCD f x dx
a
F b F a
a
b
B
x=b
x=a
0
A
y=0
x

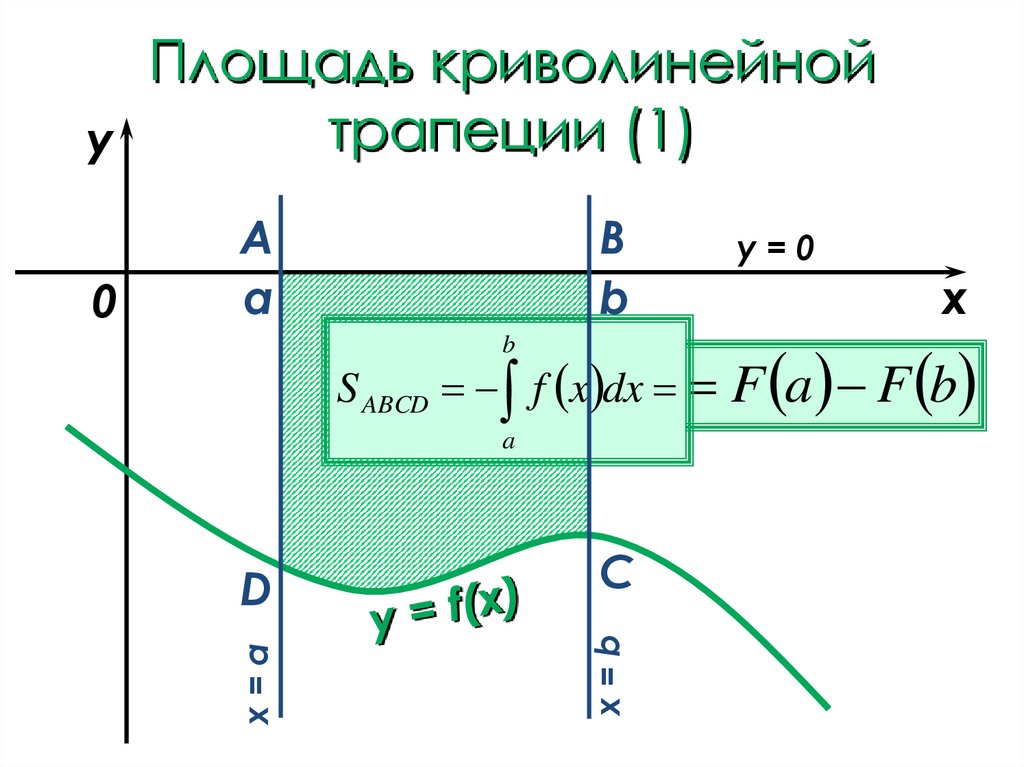
4. Площадь криволинейной трапеции (1)

y
B
b
b
y=0
S ABCD f x dx F
D
C
x=b
a
x=a
0
A
a
x
a F b

5.

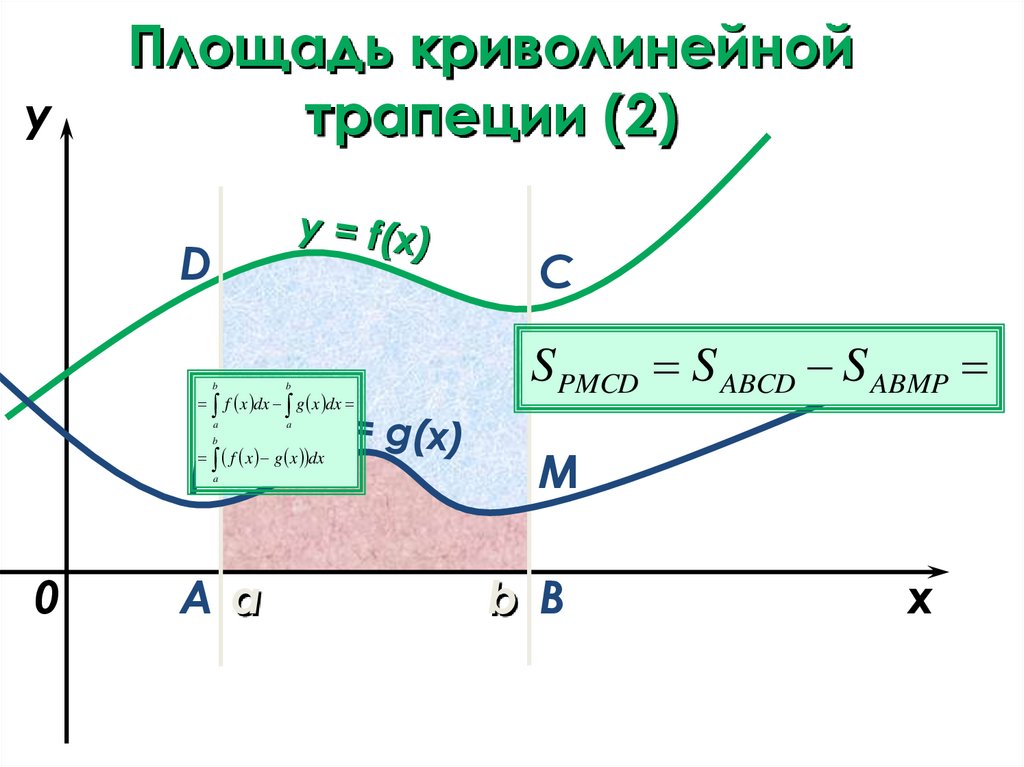
y
Площадь криволинейной
трапеции (2)
D
C
b
b
a
a
f x dx g x dx
b
f x g x dx
P
a
0
Aa
S PMCD S ABCD S ABMP
M
b B
x

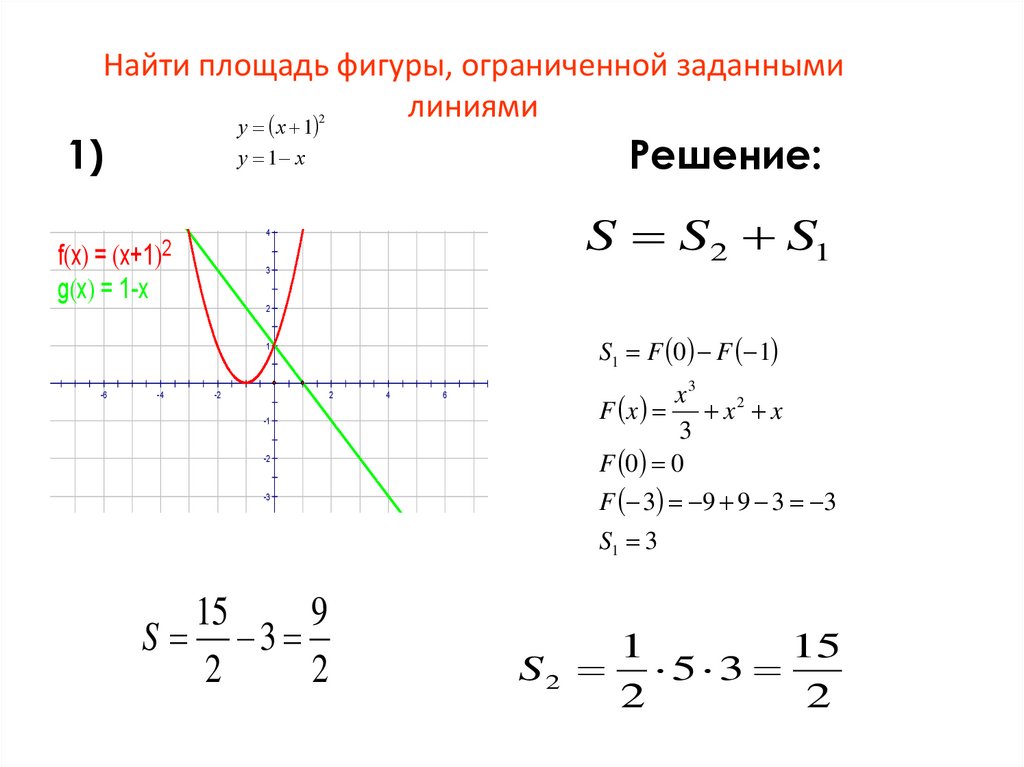
6. Найти площадь фигуры, ограниченной заданными линиями

у х 1
2
1)
Решение:
у 1 х
S S2 S1
4
f x = x+1 2
g x = 1-x
3
2
S1 F 0 F 1
1
-6
-4
-2
2
-1
-2
-3
-4
15
9
S 3
2
2
4
6
x3
F x x 2 x
3
F 0 0
F 3 9 9 3 3
S1 3
1
15
S2 5 3
2
2

7.

y
Площадь криволинейной
трапеции (3)
C
D
A
a
S PMCD S ABCD S ABMP
b
b
a
a
f x dx g x dx
0
b
f x g x dx
a
P
B
b
M
x

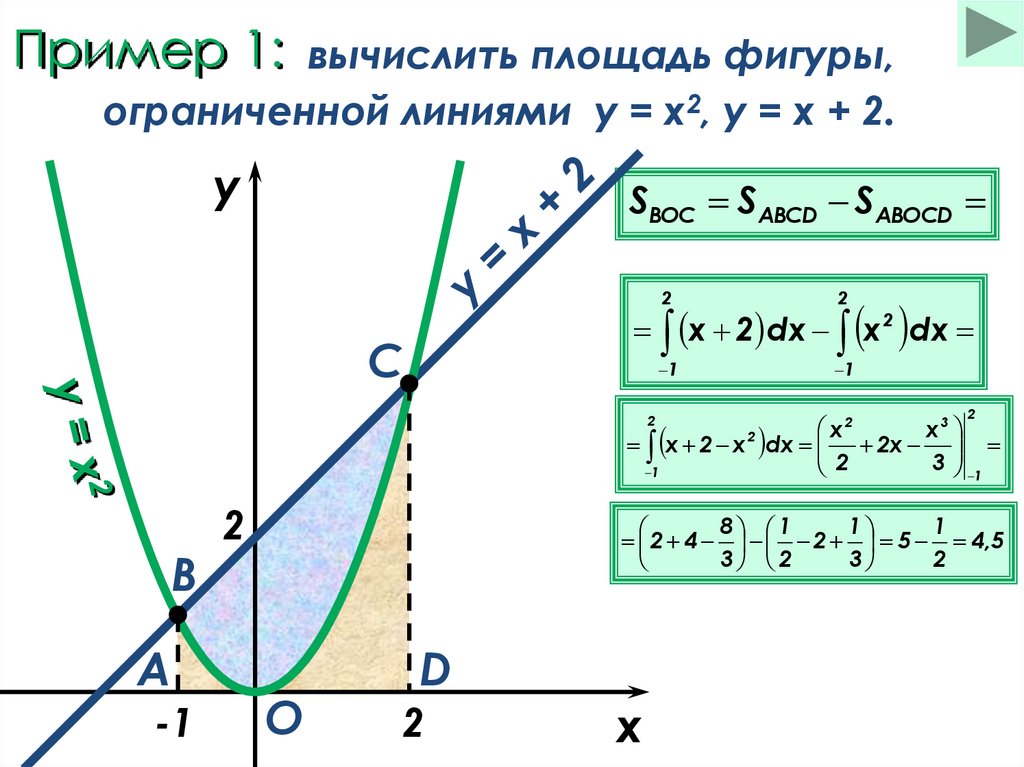
8. Пример 1:

вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
C
2
2
2
1
1
2
x
2
dx
x
dx
2
x2
x3
2
х 2 х dx 2x
3 1
2
1
B
A
-1
2
8 1
1
1
2 4 2 5 4,5
3 2
3
2
O
D
2
x

9.

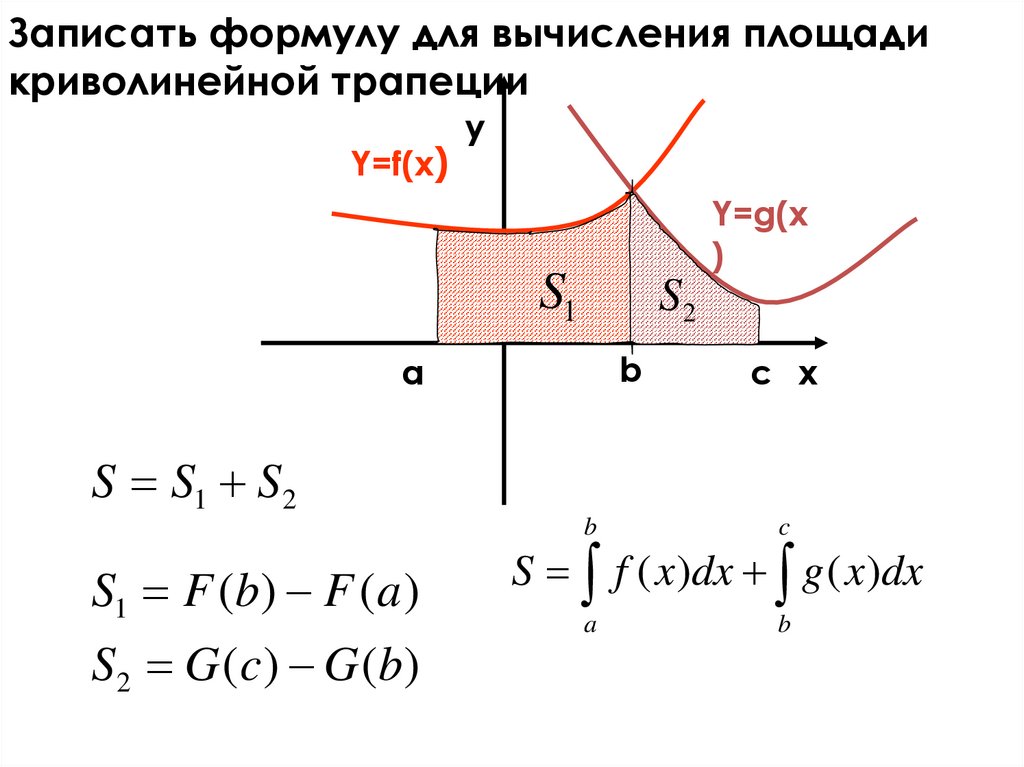
Записать формулу для вычисления площади
криволинейной трапеции
Y=f(x)
y
Y=g(x
)
S1
S2
b
a
c x
S S1 S2
S1 F (b) F ( a )
S 2 G ( c ) G ( b)
b
c
a
b
S f ( x )dx g ( x )dx

10.

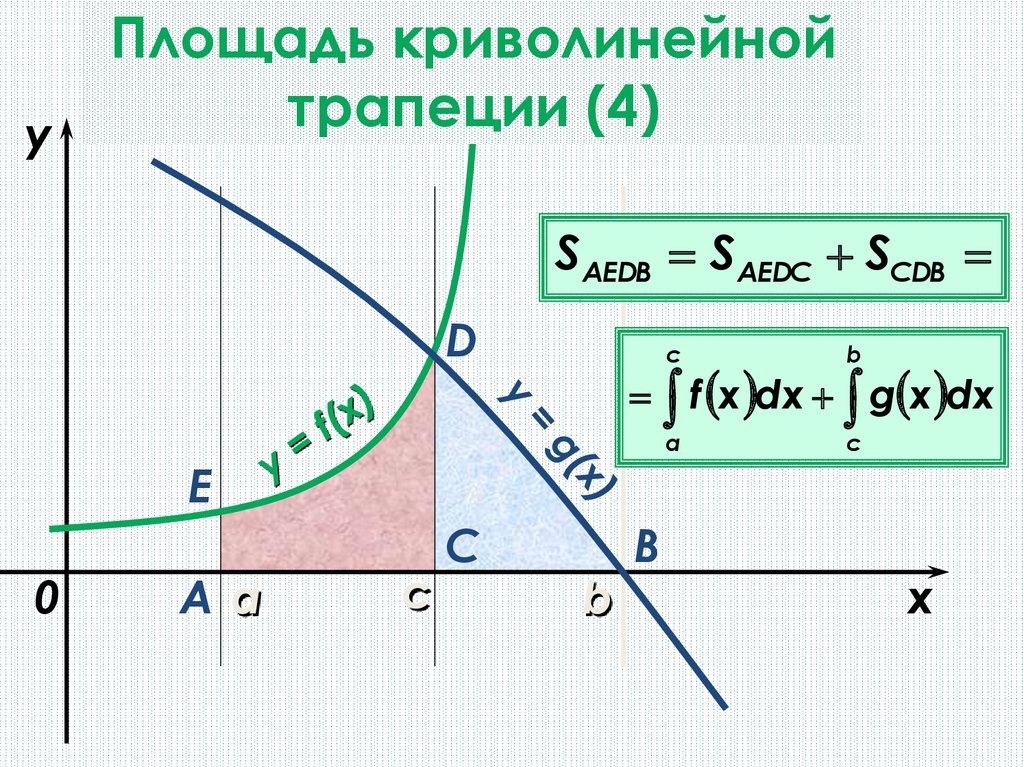
y
Площадь криволинейной
трапеции (4)
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x

11.

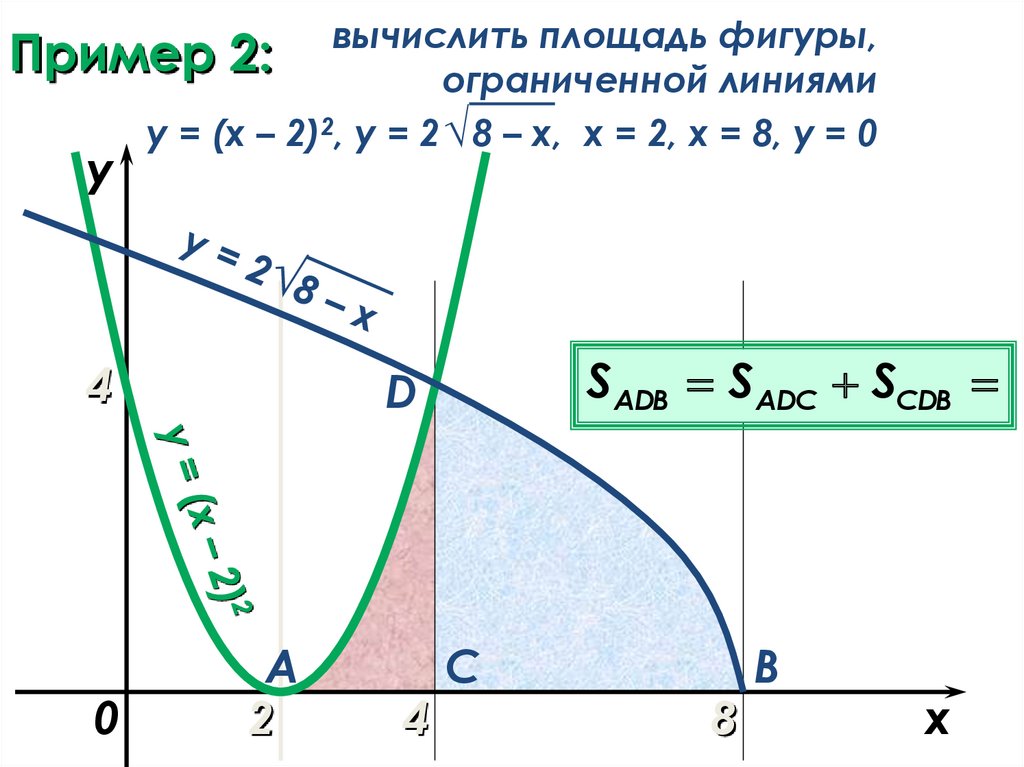
вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x

12.

вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
4
8
x - 2 dx 2
2
2
4
3 4
x 2
8 - хdx
3
4 8 x 8 x
3
2
8
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3

13.

4) Используя геометрические
соображения, вычислить интеграл:
4
а)
4 х х dx
2
0
0
б)
1
х 2 х dx
2

14.

Решение. а) Имеем:
у
4 х х2 ;
у2 4 х х2;
х 2 2 у 2 22
Это уравнение окружности радиуса r=2 с центром в точке (2;0).
Значит, заданным интегралом выражается площадь половины круга.
S 0,5 r 2 0,5 4 2
б) Имеем:
у х2 2 х ;
х 1 2 у 2 12.
S 0,25 r 2 0,25 1 0,25

15.

5) Вычислить интеграл:
2
а)
4 х 2 dx
0
4
б)
64 х 2 dx
4
5
в ) х 1 dx
0