Similar presentations:
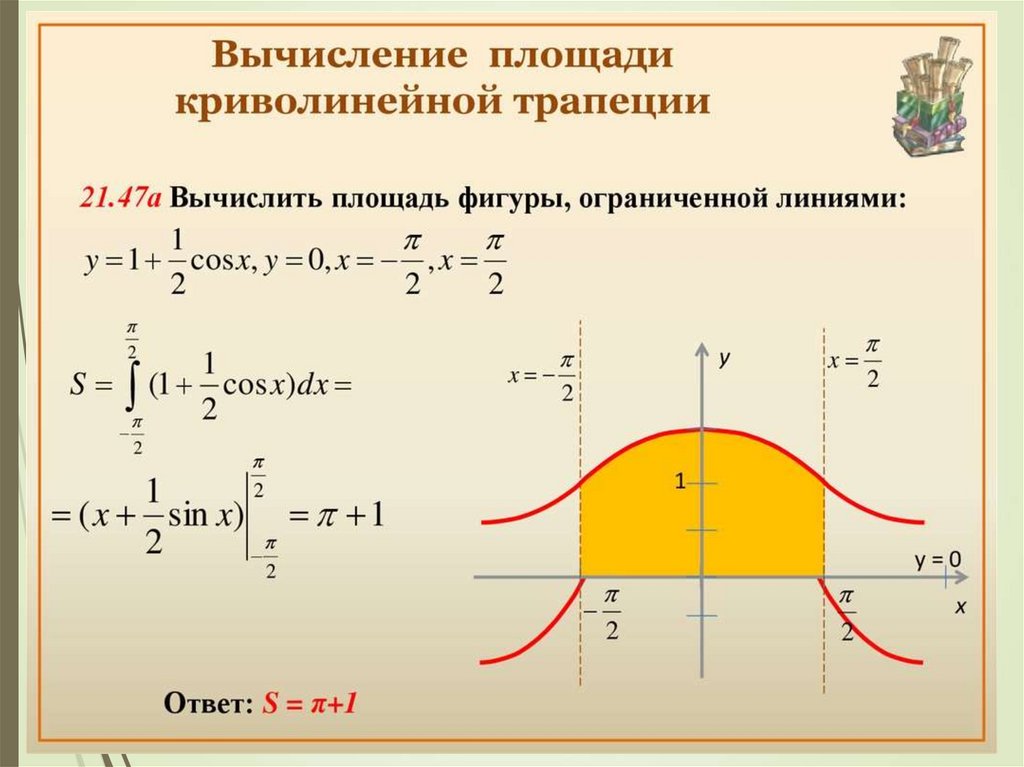
Площадь криволинейной трапеции
1.
2.
Цель занятия:Задачи занятия:
1. Проиллюстрировать практическое применение
интеграла на примерах нахождения площади
криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить
усвоение изученного материала
3. Закрепить изученное в ходе выполнения
упражнений.
3.
Вычисление площадей с помощьюинтегралов (записать в тетрадь)
1. Криволинейная трапеция, ограниченная сверху
графиком функции y=f(x), снизу осью ОХ и по бокам
отрезком [a;b]
b
S f ( x )dx
a
4.
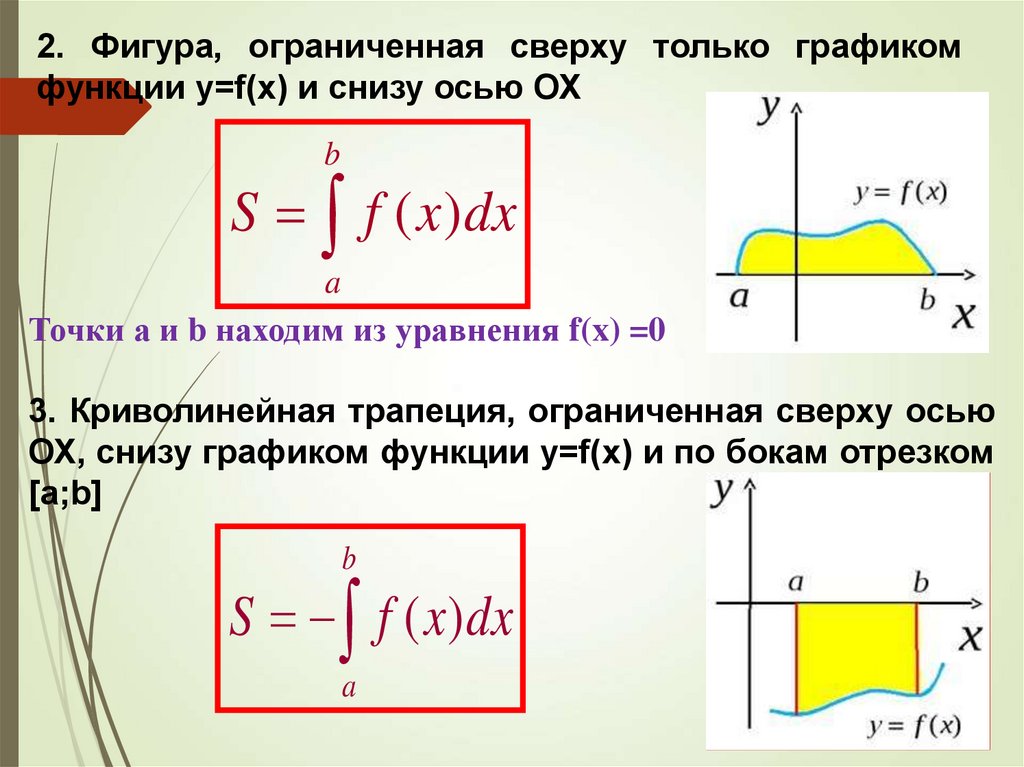
2. Фигура, ограниченная сверху только графикомфункции y=f(x) и снизу осью ОХ
b
S f ( x ) dx
a
Точки а и b находим из уравнения f(x) =0
3. Криволинейная трапеция, ограниченная сверху осью
ОХ, снизу графиком функции y=f(x) и по бокам отрезком
[a;b]
b
S f ( x ) dx
a
5.
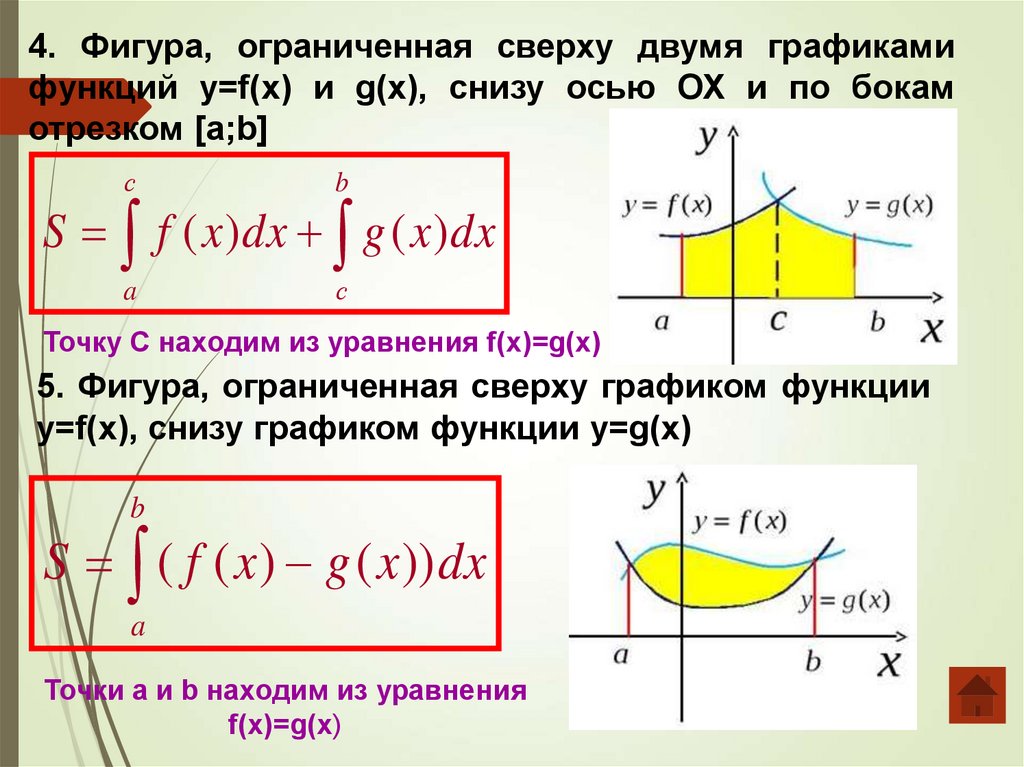
4. Фигура, ограниченная сверху двумя графикамифункций y=f(x) и g(x), снизу осью ОХ и по бокам
отрезком [a;b]
с
b
a
с
S f ( x ) dx g ( x ) dx
Точку С находим из уравнения f(x)=g(x)
5. Фигура, ограниченная сверху графиком функции
y=f(x), снизу графиком функции y=g(x)
b
S ( f ( x ) g ( x )) dx
a
Точки a и b находим из уравнения
f(x)=g(x)
6.
7.
Улыбнулись.Как я устал!!!
Всё учишь и
учишь
А для меня
урок всегда
праздник!
8.
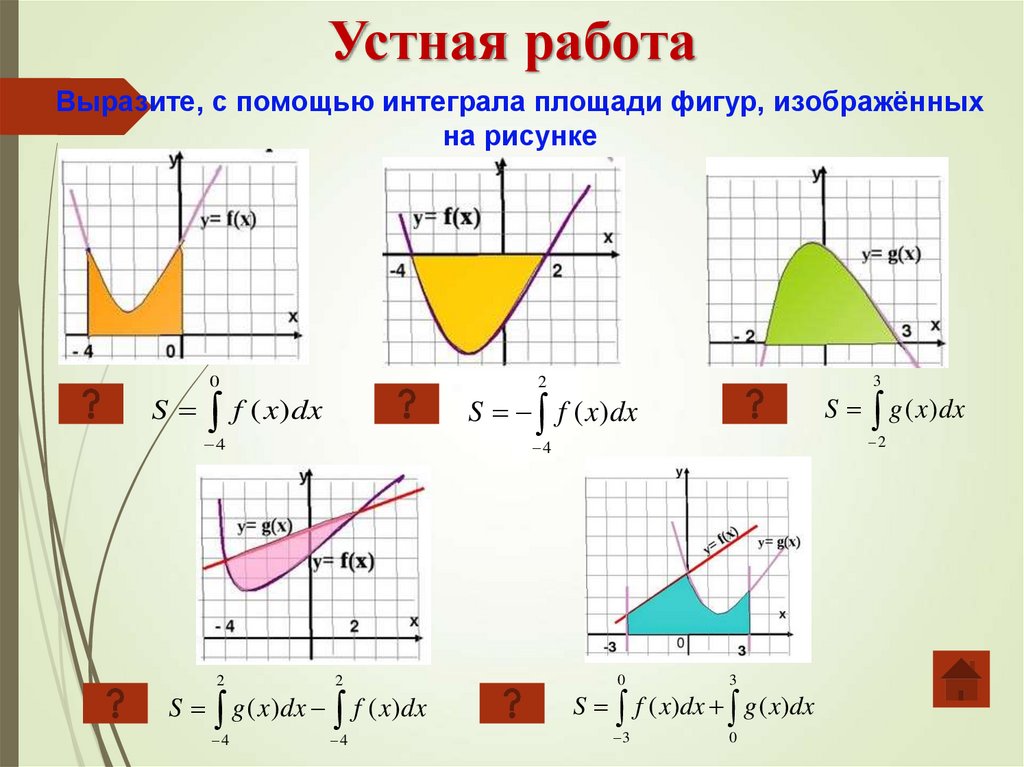
Устная работаВыразите, с помощью интеграла площади фигур, изображённых
на рисунке
0
S
3
2
f ( x)dx
S g ( x)dx
S f ( x)dx
4
2
4
2
2
4
4
S g ( x)dx f ( x)dx
S
0
3
3
0
f ( x)dx g ( x)dx
9.
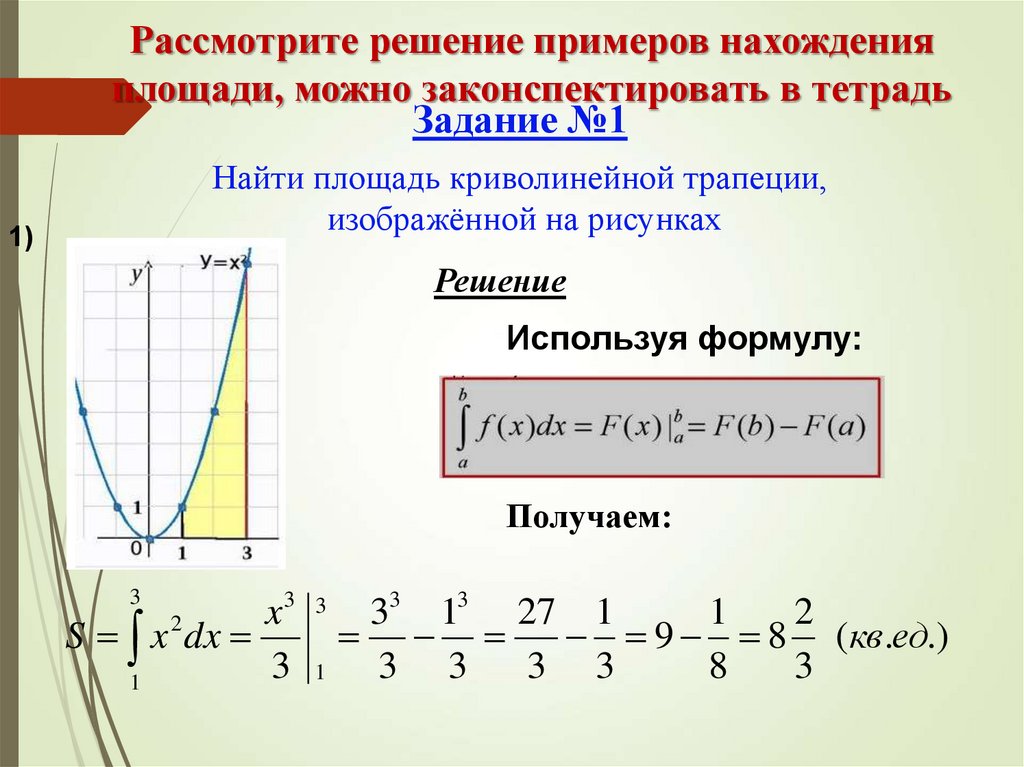
Рассмотрите решение примеров нахожденияплощади, можно законспектировать в тетрадь
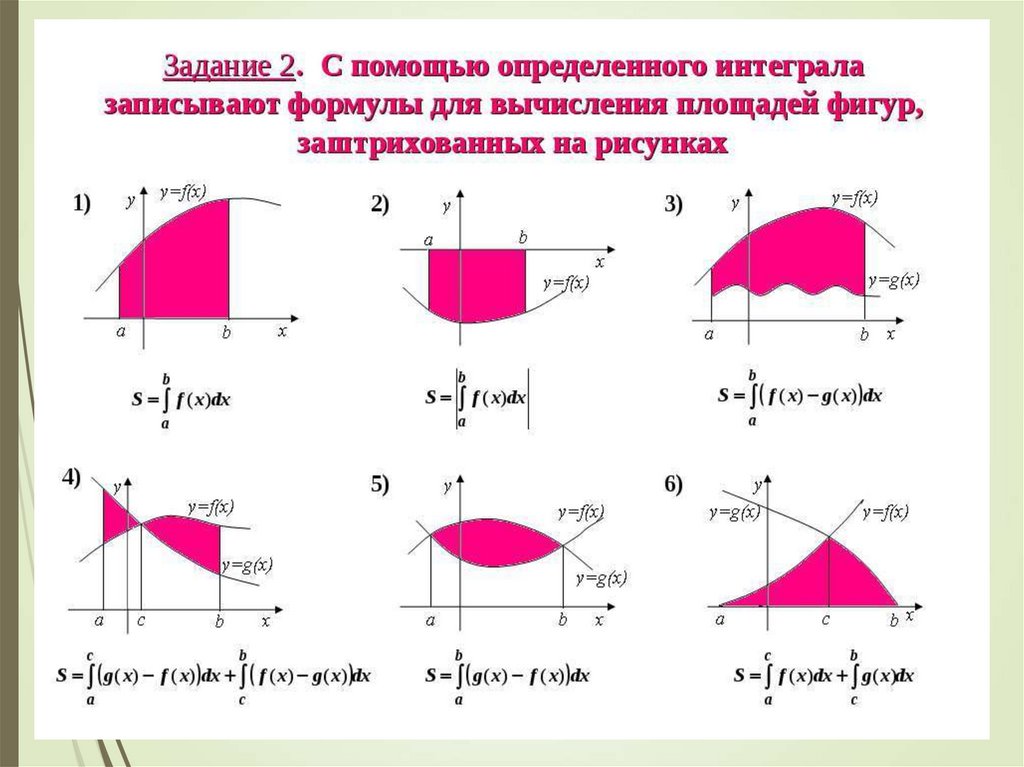
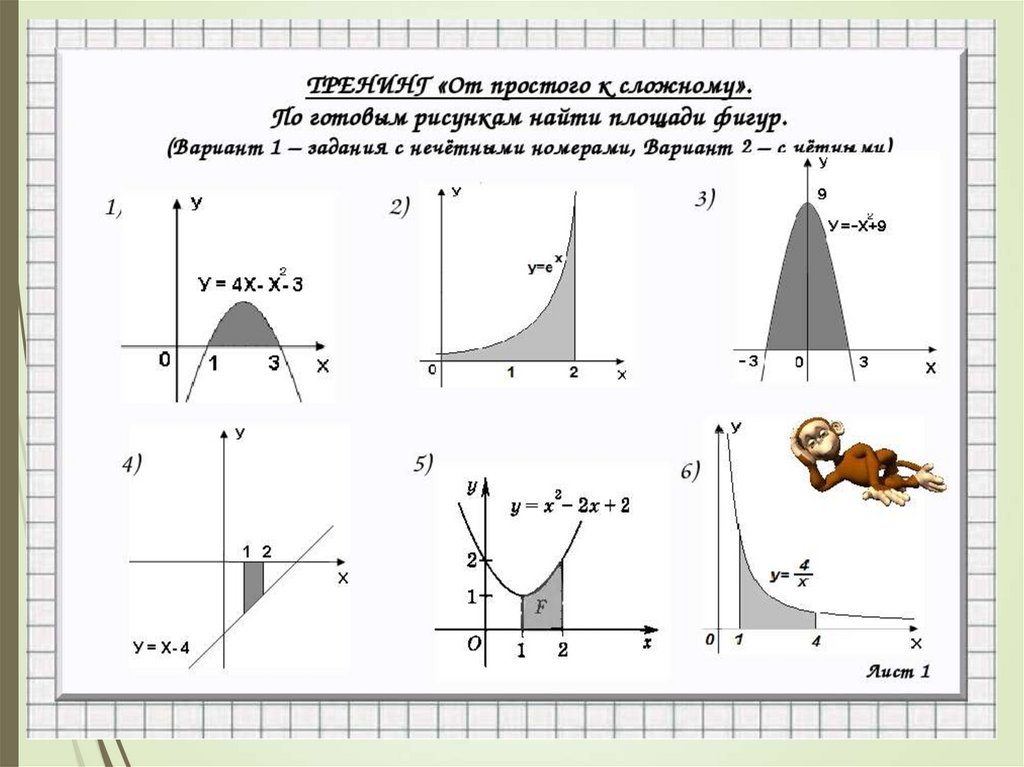
Задание №1
Найти площадь криволинейной трапеции,
изображённой на рисунках
1)
Решение
Используя формулу:
Получаем:
3
3
x
S x 2 dx
3
1
3
1
33 13 27 1
1
2
9 8 (кв.ед.)
3 3
3 3
8
3
10.
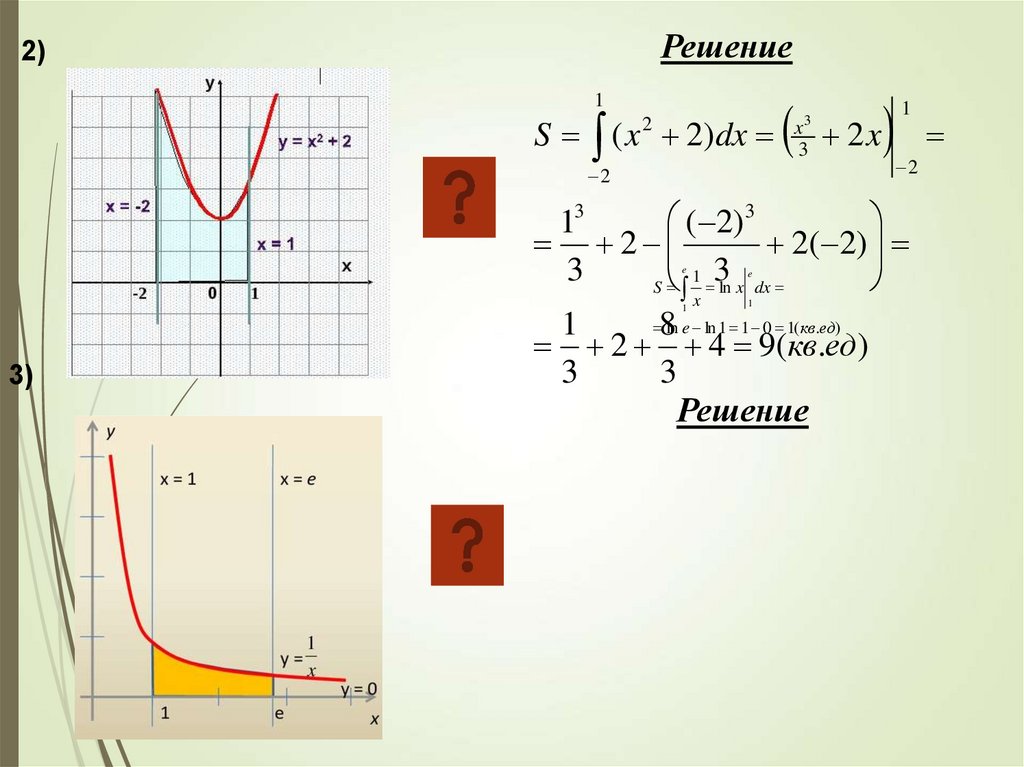
Решение2)
1
S ( x 2)dx
2
x3
3
2x
2
1
2
( 2) 3
13
2
2( 2)
3
1 3
S
ln x dx
e
e
1
1
x
3)
8
ln e ln 1 1 0 1(кв.ед)
1
2 4 9(кв.ед)
3
3
Решение
11.
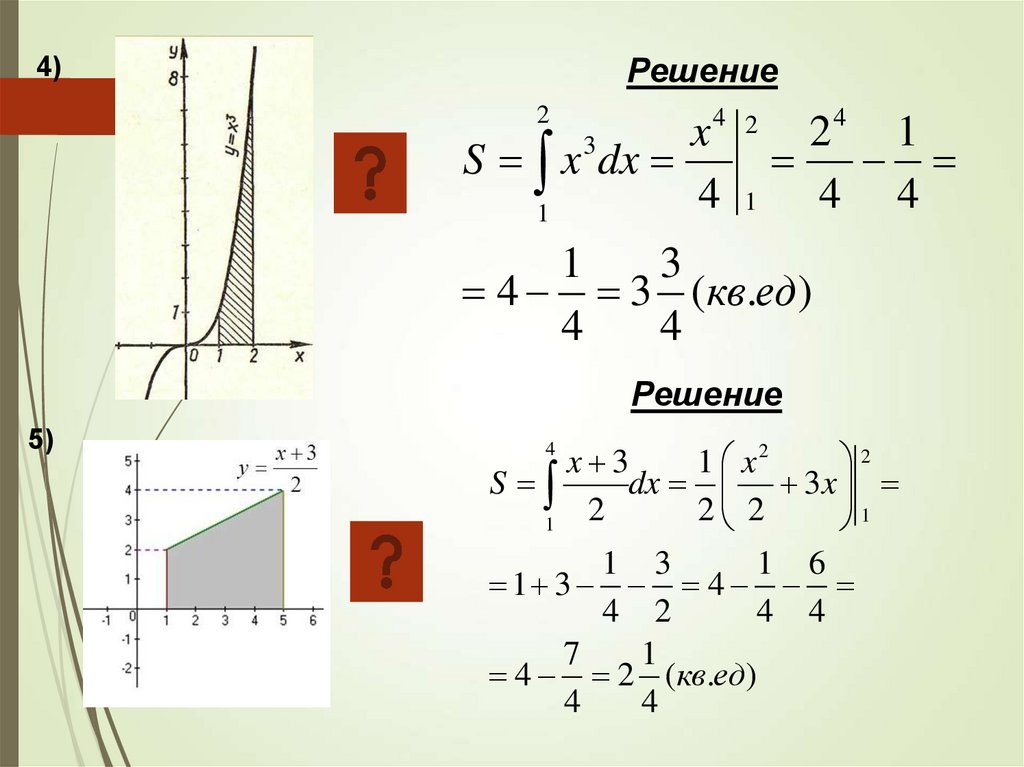
Решение4)
2
4
x
S x 3 dx
4
1
2
1
24 1
4 4
1
3
4 3 (кв.ед)
4
4
Решение
5)
2
x 3
1 x2
S
dx 3x
2
2 2
1
1
4
1 3
1 6
1 3 4
4 2
4 4
7
1
4 2 (кв.ед)
4
4
12.
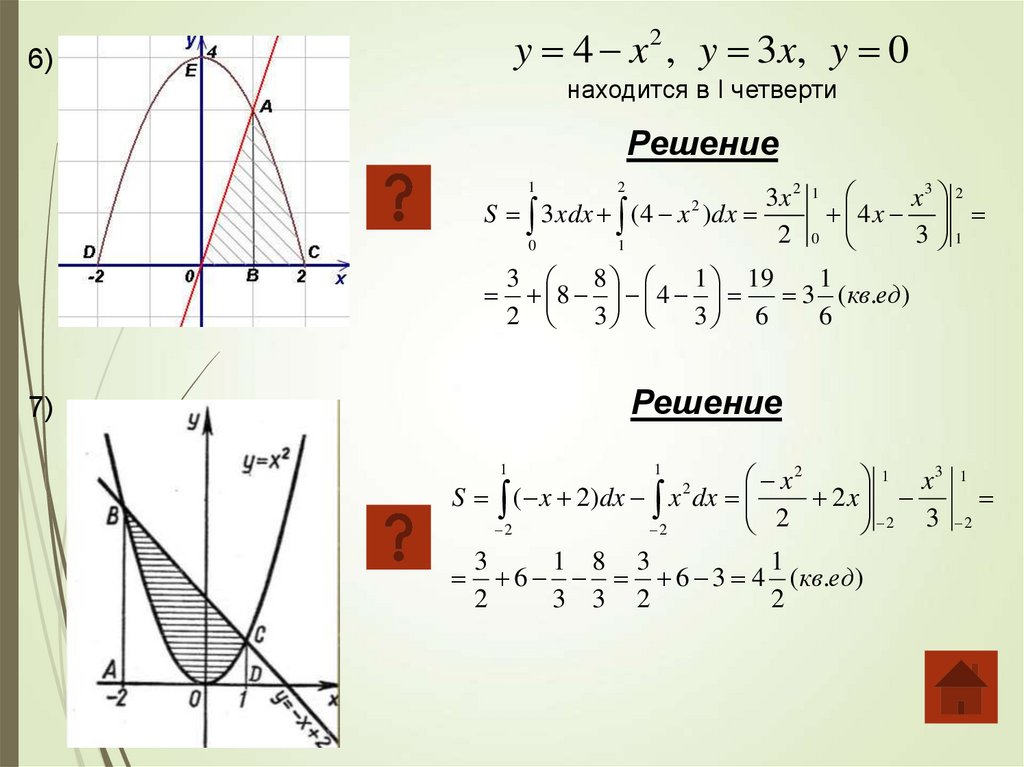
y 4 x 2 , y 3x, y 06)
находится в I четверти
Решение
3x 2 1
x3 2
S 3 xdx (4 x )dx
4 x
2
3 1
0
0
1
3 8
1 19
1
8 4
3 (кв.ед)
2 3
3 6
6
1
2
2
Решение
7)
x2
1 x3
S ( x 2)dx x dx
2 x
2
2 3
2
2
3
1 8 3
1
6 6 3 4 (кв.ед)
2
3 3 2
2
1
1
2
1
2
13.
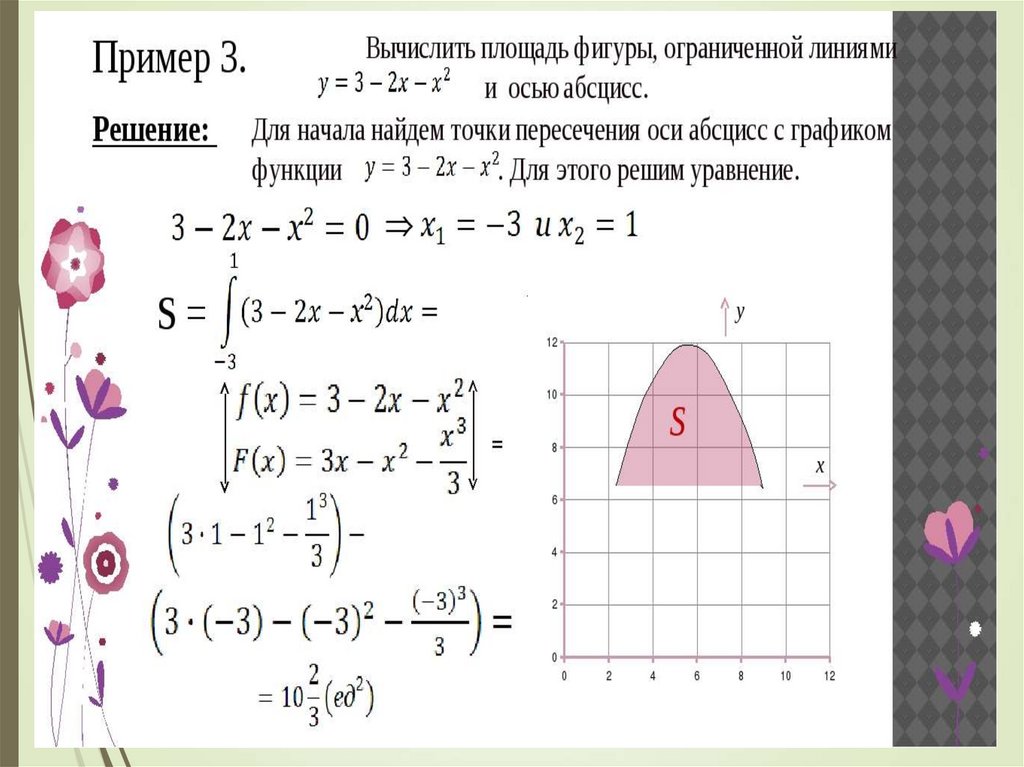
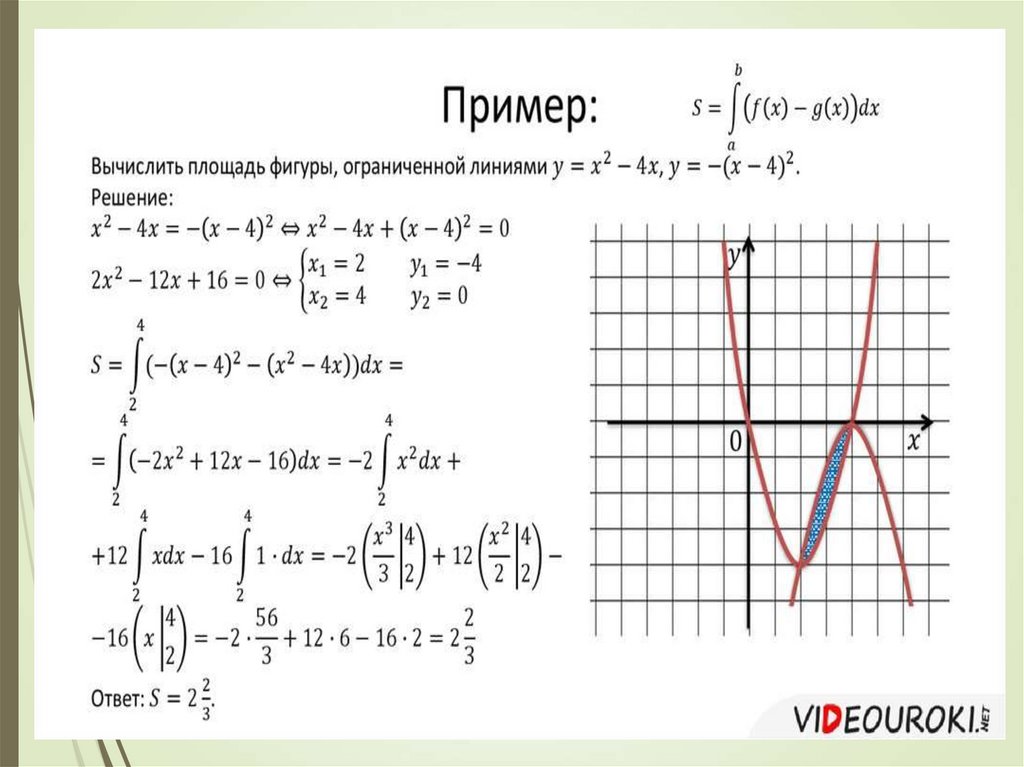
14. Рассмотрите примеры, можно оформить в тетрадь.
15.
16.
17.
18.
Выполните заданияЗАДАНИЕ №1
Задания
Ответы
Вычислить площадь фигуры, ограниченной
линиями
1 Вариант
2 Вариант
1
2
3
4
y=x2+2, y=x+2
y= -x2+4, y= -x+4
7
1/6
2/3
1/3
y=sin 2x, y=0, x=0,
x=π/4
y=cos 2x, y=0,
x= -π/4, x=π/4
2
-1
1/2
1
y= -2/x, y=2,
x= -4, x= -1
y= -1/x, y=1,
x= -3, x= -1
6-4ln2
2-ln3
2ln2
2-3ln2
Выберите верный вариант ответа
19.
ЗАДАНИЕ №2Вычислите площадь фигуры, ограниченной линиями
(схематично изобразив графики функций).
1) y 6 x x 2 , y 6 2 x
2) y 2 x 2 , y x 1
3) y 1 x, y 3 2 x x 2
4) y x 2 , y x
ЗАДАНИЕ №3
Вычислить площадь фигуры, ограниченной
линиями и осью ОХ, если
1) y 6 ( x x )
2
2) y 7 x x 10
2
20.
Задание 4.Вычислить площадь фигуры, ограниченной линиями,
предварительно сделав рисунок 1 вариант (нечётные)
2 вариант (чётные) 7 задание дополнительно
1) y x 2 ( x 0), y 1, y 4, x 0
2) y x 2 4 x 8, y 3 x 2 x 3 , если x [ 2;3]
3) y 3 x 1, y 9 x
4) y x 4 x 4, y 10, x 3, x 0
2
5) y x, y 5 x, x 1, x 2
6) y x 2 4 x 2, y x 2
7) y sin x, x
6
,x
3
21. Фото решений отправить удобным способом.
22.
Контрольные вопросы:1. Какая функция называется первообразной для функции
f(x)?
2. Чем отличаются друг от друга различные первообразные
функции для данной функции f(x)?
3. Дайте определение неопределённого интеграла.
4. Как проверить результат Какое действие называется
интегрированием?
5. интегрирования?
6. Дайте определение определённого интеграла.
7. Сформулируйте теорему Ньютона-Лейбница.
8. Перечислите свойства интеграла.
9. Как вычислить площадь плоской фигуры с помощью
интеграла (составьте словесный алгоритм)?
10.Перечислите области применения интеграла, назовите
величины, которые можно вычислить с помощью интеграла.
23.
Подведём итоги1. Познакомились с понятиями криволинейной
трапеции и определённого интеграла.
2. Научились вычислять по формуле НьютонаЛейбница площадь криволинейной трапеции,
используя знания о первообразной и правила её
вычисления.
3. Закрепили
изученное
практических заданий.
в
ходе
выполнения
4. Проверили усвоение изученного материала











 mathematics
mathematics








