Тригонометрия. Леонард Эйлер

1.

2.

Тригономе́трия (от греч. τρίγονο (треугольник) и греч.
μετρειν (измерять),
то есть измерение треугольников) — раздел
математики,
в котором изучаются тригонометрические функции и
их приложения к геометрии.
Данный термин впервые появился в 1595 г. как
название книги немецкого математика Бартоломеуса
Питискуса (Bartholomäus Pitiscus, 1561—1613),
а сама наука ещё в глубокой древности
использовалась для расчётов в астрономии,
геодезии и архитектуре.

3.

Эти ученые внесли свой вклад в развитие тригонометрии
Архимед
Жозеф Луи
Лагранж
Фалес

4.

Тригонометрия возникла и развивалась в древности как один
из разделов астрономии, как ее вычислительный аппарат,
отвечающий практическим нуждам человека. С ее помощью
можно определить расстояние до недоступных предметов и
существенно упрощать процесс геодезической съемки
местности для составления географических карт.
Общепринятые понятия тригонометрии, а также обозначения и
определения тригонометрических функций сформировались в
процессе долгого исторического развития.
Тригонометрические сведения были известны древним
вавилонянам и египтянам, но основы этой науки заложены в
Древней Греции, встречающиеся уже в III веке до н.э.
в работах великих математиков – Евклида, Архимеда,
Апполония Пергского. Древнегреческие астрономы успешно
решали вопросы из тригонометрии, связанные с астрономией.

5.

Тригонометрия – математическая дисциплина, изучающая
зависимость между сторонами и углами треугольника.
Тригонометрические вычисления применяются
практически во всех областях геометрии, физики
и инженерного дела, при измерении расстояний
до недалёких звёзд в астрономии, между
ориентирами в географии, при контроле системы
навигации, в теории музыки, акустике, оптике,
электронике, теории вероятностей, статистике,
биологии, медицине (включая ультразвуковое
исследование (УЗИ) и компьютерную
томографию), фармацевтике, химии,
сейсмологии, метеорологии, океанологии,
картографии, архитектуре, экономике,
электронной технике, машиностроении,
компьютерной графике.

6.

7.

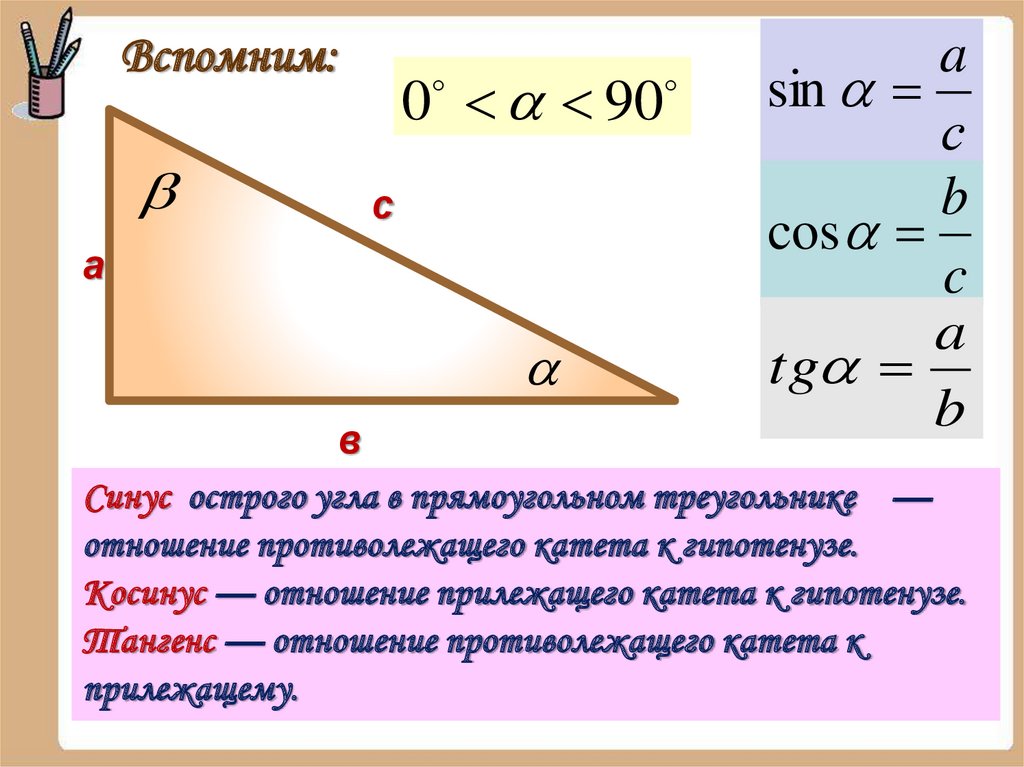
Вспомним:
0 90
с
а
a
sin
с
b
cos
c
a
tg
b
в
Синус острого угла в прямоугольном треугольнике —
отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к
прилежащему.

8.

В XVIII веке Леонард Эйлер
дал современные, более
общие определения,
расширив область
определения этих функций
на всю числовую ось.
угол _ поворота
R

9.

у
1
0
х
1

10.

у
1
0
х
1

11.

Рассмотрим в прямоугольной системе координат
окружность единичного радиуса и отложим от
горизонтальной оси угол
(если величина угла положительна, то откладываем против
часовой стрелки, иначе по часовой стрелке). Точку
пересечения построенной стороны угла с окружностью
у
обозначим Р.
0
Р
1
0
1
х
1
0

12.

Р90
у
Р60
Р45
Р30
Р180
Р
1
0
х 0
1
Р270
Р360

13.

Радианная мера угла
R
С
центральный угол
R – радиус
С – длина дуги
Если R = C,
то центральный угол равен
одному радиану
Радианной мерой угла называется
отношение длины соответствующей дуги
к радиусу окружности
1 рад 57

14.

n
180
180
n
n 60
4
60
180
3
60
3
180
180
180
n 4
45
4
4
45
4

15.

cos
у
1
P ( x; y)
у
sin
1
0
P (1;0)
х 0
1
х
1

16.

sin y
Синус угла определяется как ордината
точки P
cos x
Косинус — абсцисса точки P
y
tg к абсциссе
Тангенс – отношение ординаты
x
точки P
x
Котангенс – отношение абсциссы
ctg к ординате
точки P
y

17.

• В курсе геометрии вы познакомились с тангенсом
острого угла, равным частному синуса и косинуса
этого угла:
tg φ = sin φ/cosφ
• С помощью этого равенства можно определить
тангенс любого угла φ, косинус которого отличен от
нуля.
• Тангенсом угла назывется частное синуса к
косинусу этого угла.
• Для углов, косинусы которых равны 0, т. е. углов
вила π/2 + πn (n – любое число), тангенс не
существует.

18.

• На рисунке к единичной окружности в
точке P0 проведена касательная; Pφ –
конечная точка поворота на угол φ; C –
точка пересечения касательной и
прямой OP φ.
• Ордината точки С равна тангенсу угла
φ

19.

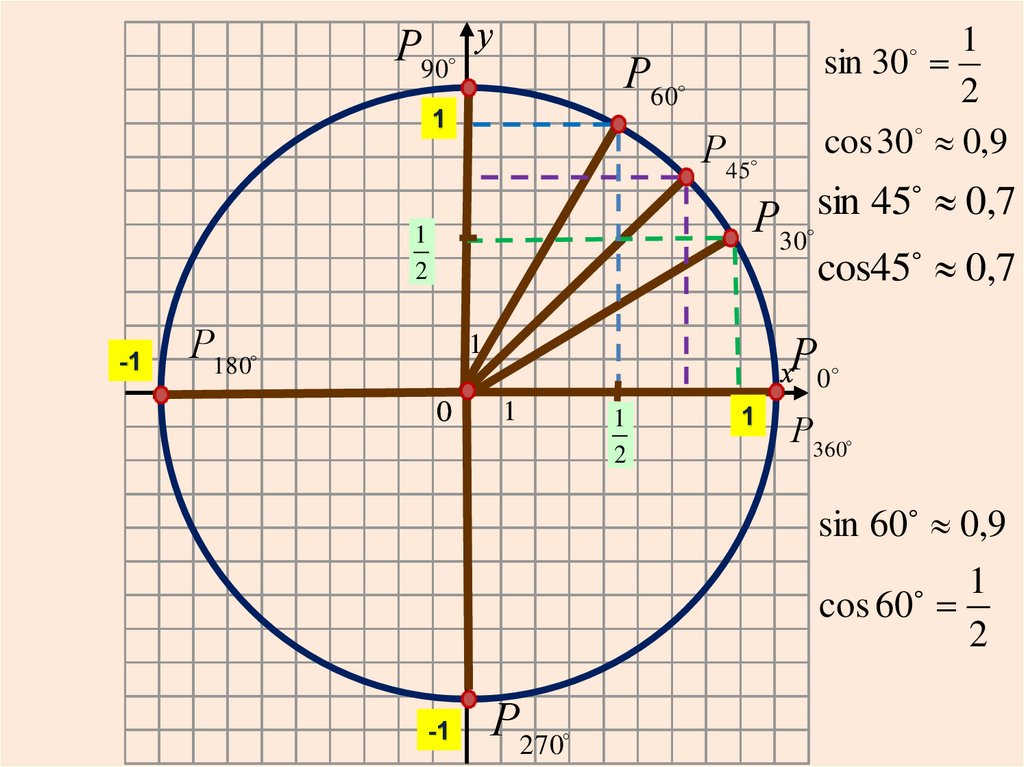
Р90
у
Р60
1
Р45
sin
45
0,7
Р30
cos45 0,7
1
2
-1
1
sin 30
2
cos 30 0,9
Р180
Р
1
0
х 0
1
1
2
1
Р360
sin 60 0,9
1
cos 60
2
-1
Р270

20.

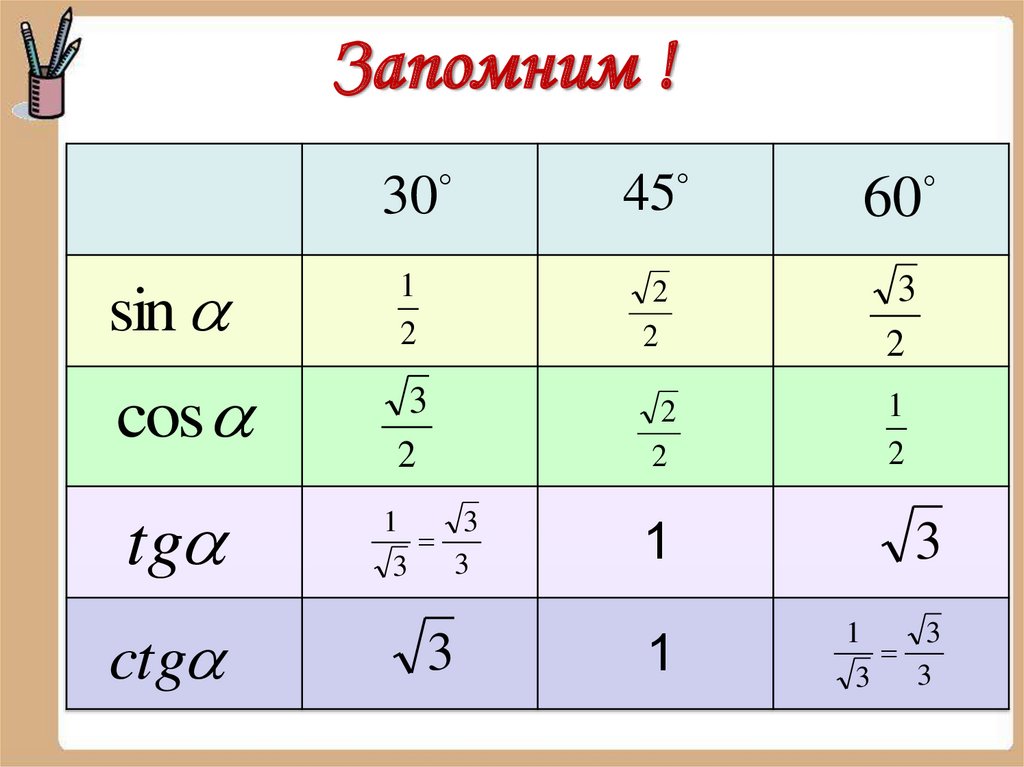
Запомним !
cos
tg
ctg
45
60
1
2
2
2
3
2
3
2
2
2
1
2
30
sin
1
3
3
3
3
1
3
1
1
3
3
3

21.

Р90
у
Р0 (1; 0)
Р90 (0; 1)
Р180
Р
1
0
х 0
1
Р360
Р180 (-1; 0)
Р270
Р270 (0;-1)

22.

Проверим:
180
270
0
-1
0
0
-1
0
1
0
-
0
-
0
-
0
-
0
-
sin
0
0
90
1
cos
1
tg
ctg
360

23.

Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
у
у
+ +
х
1
- у
0
1
1
1
- +
+ 1
1
0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
х
х
sin68 0
- +
+ 0
- +
- +
1
1
0
у
х