Similar presentations:
Тригонометрические функции числового аргумента
1.
«Тригонометрическиефункции числового
аргумента»
2.
В XVIII веке Леонард Эйлердал современные, более
общие определения,
расширив область
определения этих функций
на всю числовую ось.
угол _ поворота
R
3.
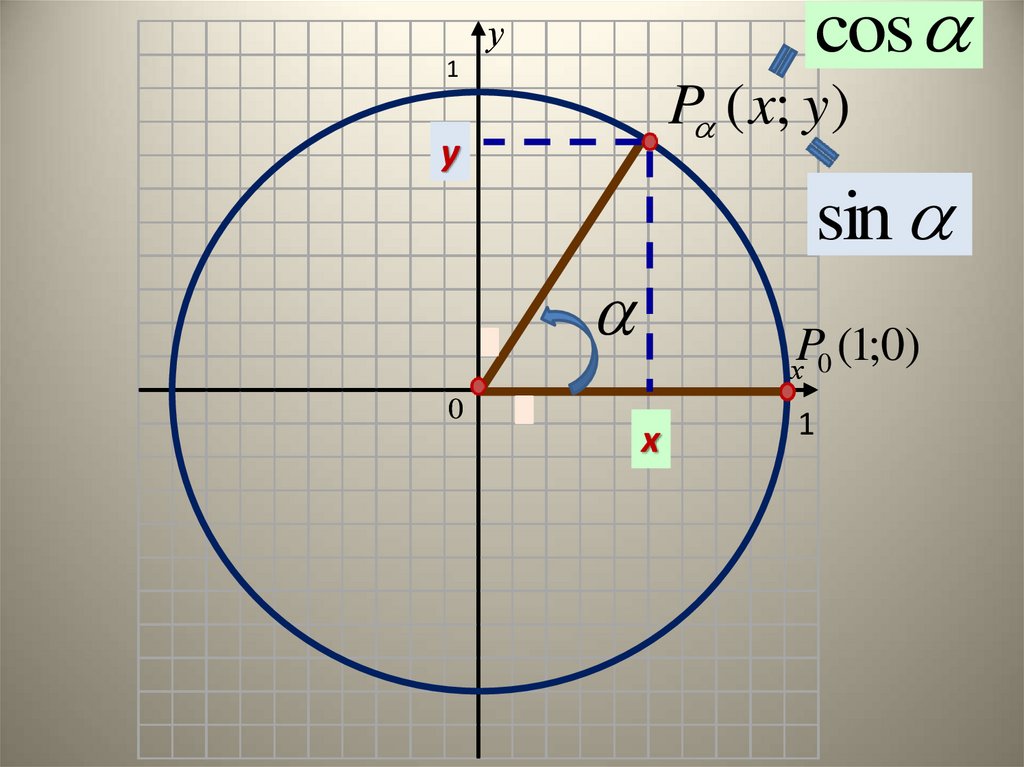
cosу
1
P ( x; y)
у
sin
1
0
P (1;0)
х 0
1
х
1
4.
sin yСинус угла определяется как ордината
точки P
cos x
Косинус — абсцисса точки P
y
tg
Тангенс – отношение
ординаты к абсциссе
точки P x
x
Котангенс – отношение
абсциссы
к
ординате
ctgточки
P
y
5.
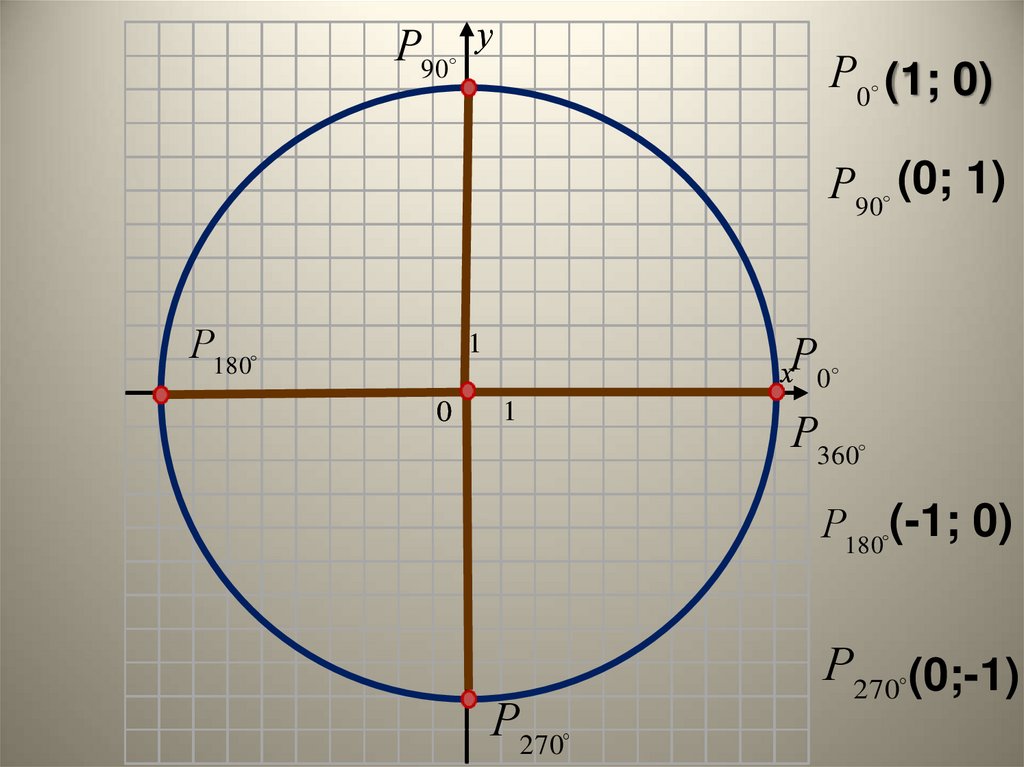
Р90у
Р0 (1; 0)
Р90 (0; 1)
Р180
Р
1
0
х 0
1
Р360
Р180 (-1; 0)
Р270
Р270 (0;-1)
6.
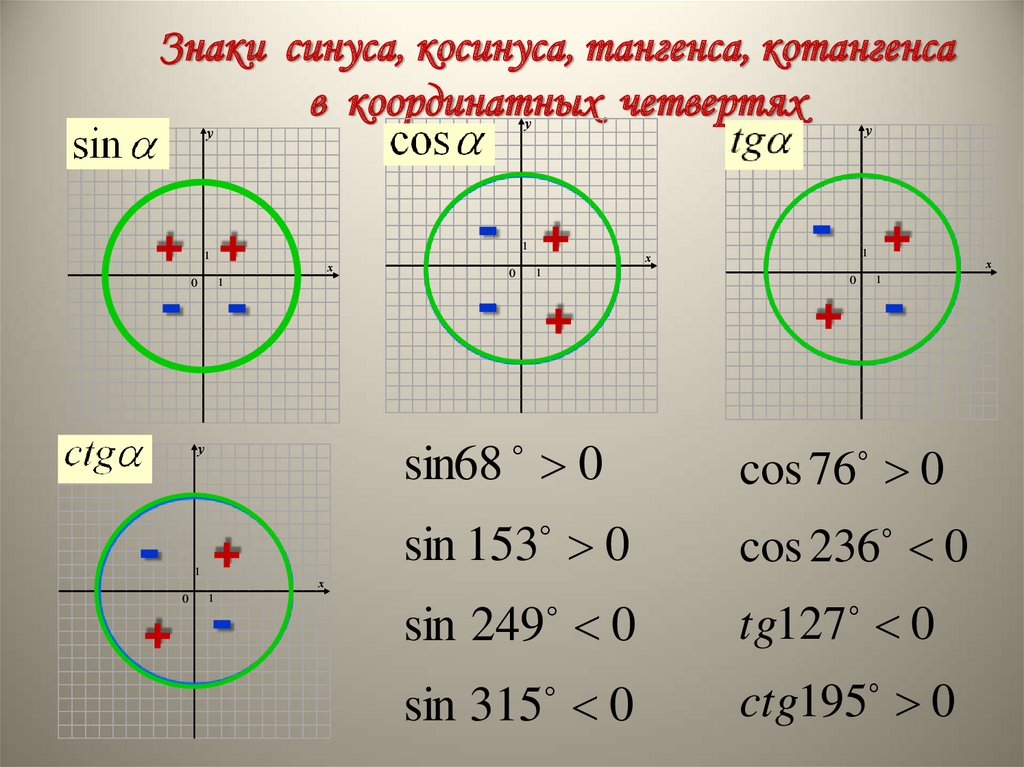
Знаки синуса, косинуса, тангенса, котангенсав координатных четвертях
у
у
+ +
х
1
- -
0
1
- +
+ 1
1
х
- +
+ 1
1
0
sin68 0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
у
0
- +
- +
1
1
0
у
х
х
7.
Четность, нечетность синуса, косинуса,тангенса, котангенса
sin( ) sin
tg ( ) tg
Нечетные функции
ctg ( ) ctg
cos( ) cos
Четная функция
8.
Периодичность тригонометрическихфункций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются
T – период
Для синусаи косинуса:T=2π
Для тангенса и котангенса: T=2π
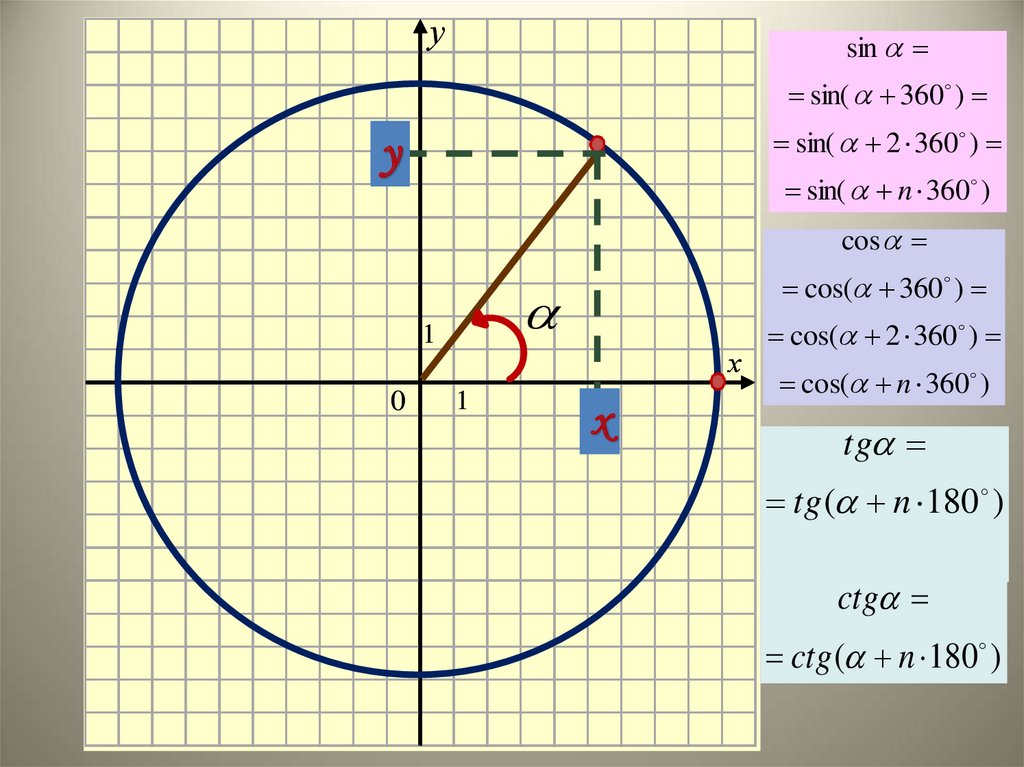
9.
уsin
sin( 360 )
sin( 2 360 )
у
sin( n 360 )
cos
1
0
cos( 360 )
х
1
х
cos( 2 360 )
cos( n 360 )
tg
tg ( n 180 )
ctg
ctg ( n 180 )
10.
у3
sin 60
2
1
cos 60
2
3
2
60
1
0
1
420 ?
sin 780
х
1
2
1
2
cos420
cos780 ?
sin
sin 780
420
sin( 60
2 360 )
sin( 60 360 )
sin 60
sin 60
3
2 23
cos 780
cos
420
360 ))
cos(
cos(60
60 2360
11
cos
60
cos 60
22
11.
sin 765cos 1110
sin( 45 2 360 )
cos(30 3 360 )
2
sin 45
2
3
cos 30
2
1
sin( 1470 ) sin 1470 sin( 30 4 360 ) sin 30
2
1
cos( 1140 ) cos1140 cos(60 3 360 ) cos 60
2
sin( 810 ) sin 810 sin( 90 2 360 ) sin 90 1
cos( 1170 ) cos1170 cos(90 3 360 ) cos 90 0
12.
sin( ) sin4
4
2
2
sin 2,5 sin( 0,5 2 ) sin 0,5 sin
2
1
9
1
2
cos( ) cos( 2 ) cos( 2 ) cos 4
4
4
4
2
13
1
3
tg
tg (2 ) tg ( 2 ) tg
6
6
6
6
3
7
1
ctg ( ) ctg (2 ) ctg ( 2 ) ctg 3
3
3
3
3


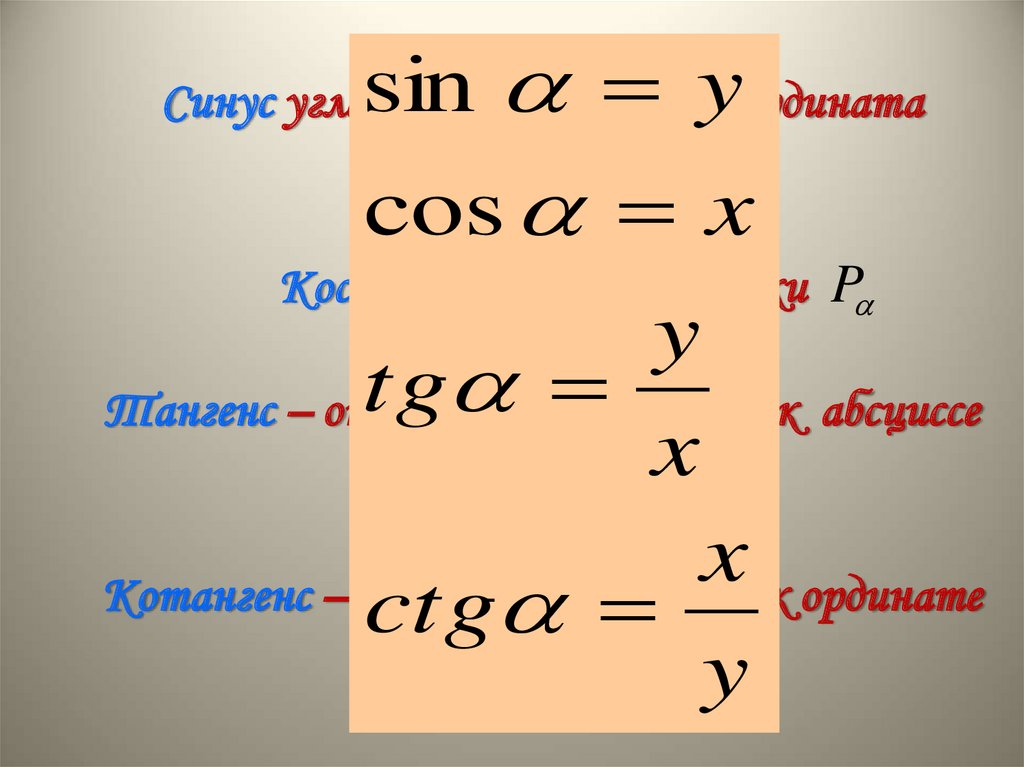



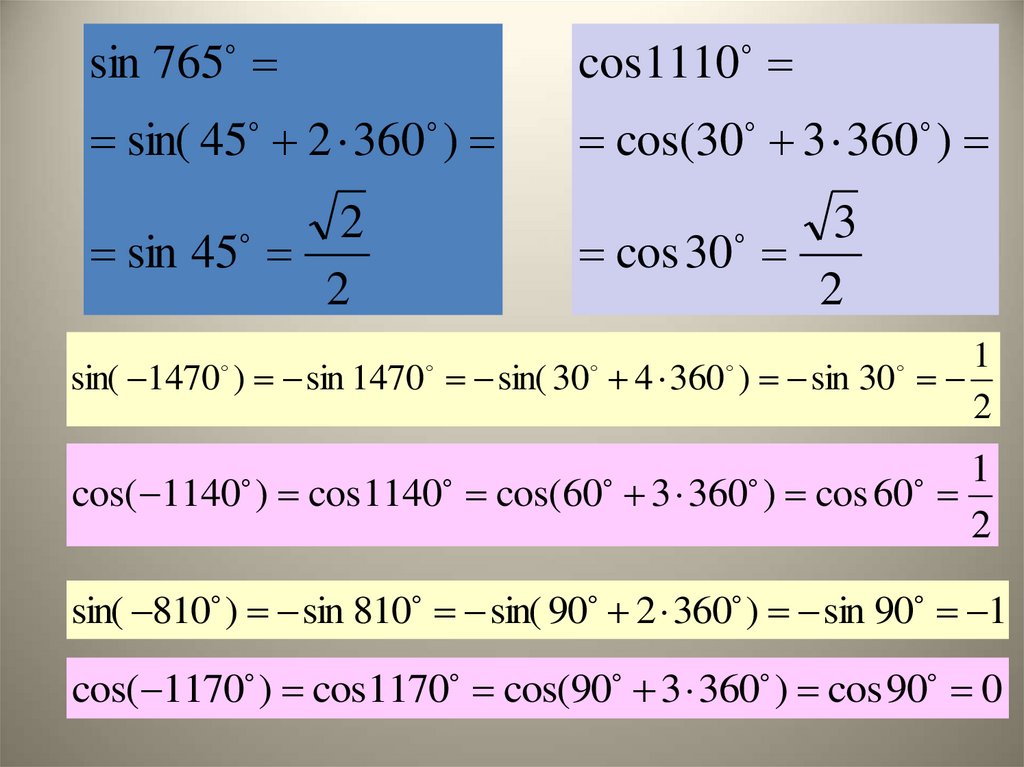
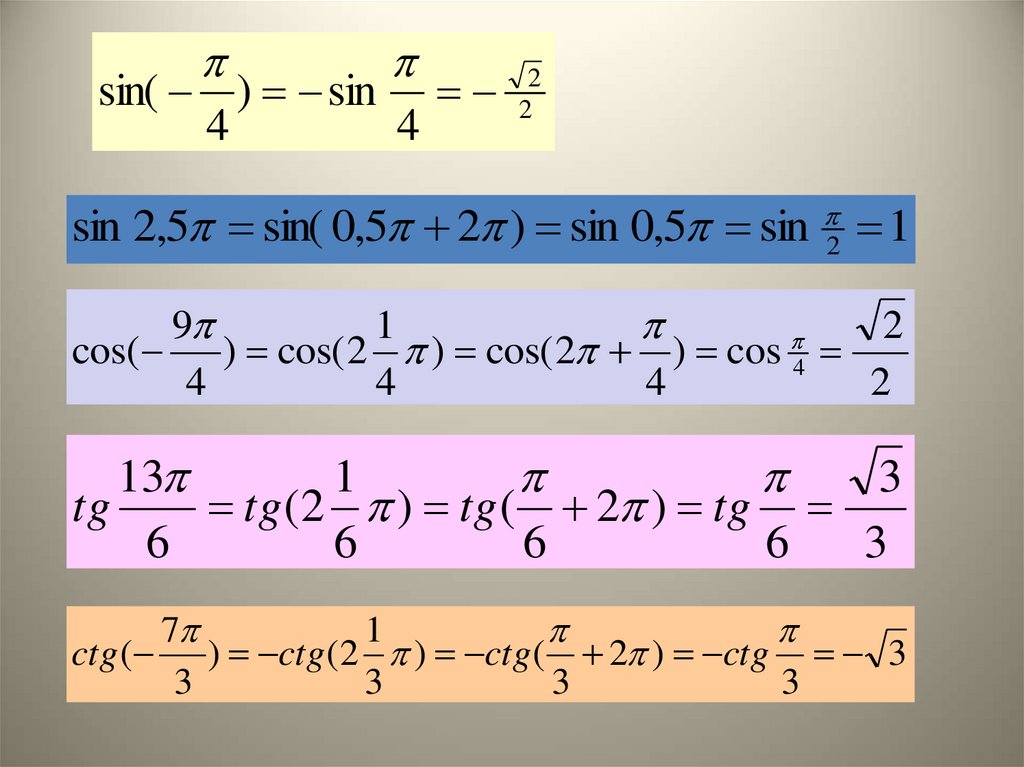
 mathematics
mathematics








