Основы специальной теории относительности

1.

основы специальной
теории относительности
Преобразования Галилея.
Постулаты специальной теории
относительности (С Т О).
Преобразования Лоренца, следствия из
преобразований Лоренца.
Релятивистская динамика.
Взаимосвязь массы и энергии.

2.

Преобразования Галилея
Это преобразования координат и времени при переходе от одной ИСО к
другой, движущейся поступательно.
В классической механике расстояние
между двумя точками и промежутки
времени между двумя событиями
инвариантны по отношению к выбору СО. Это означает: размеры тел не
зависят от скорости его движения, а
ход времени в всех СО одинаков.

3.

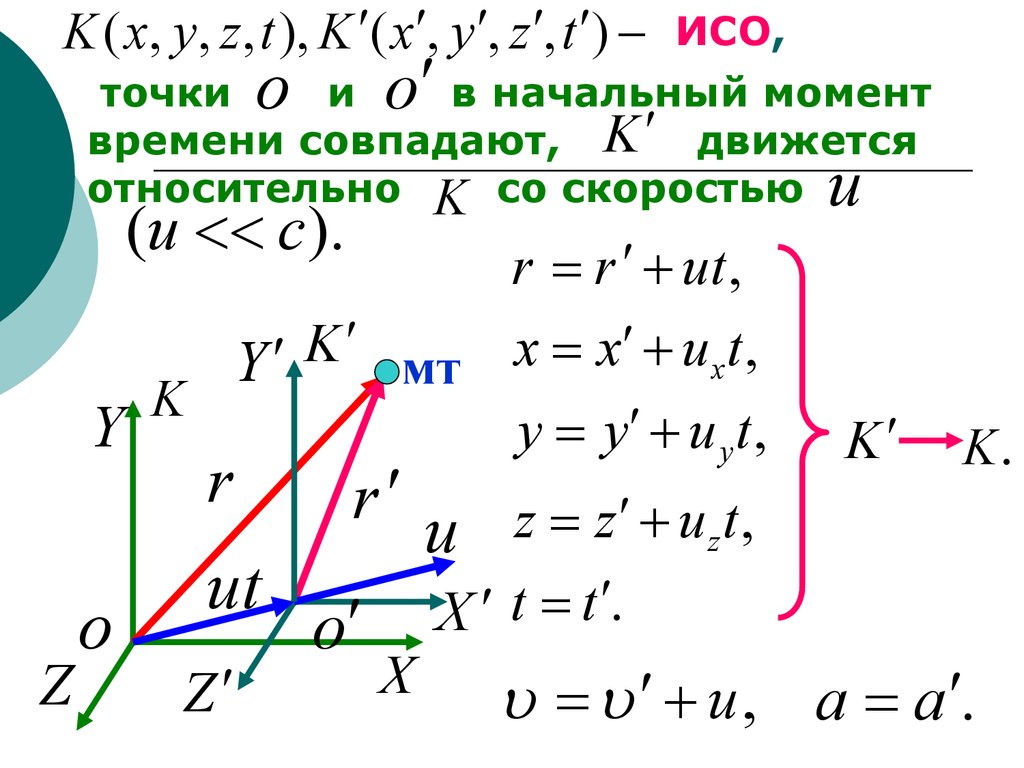
K ( x, y, z , t ), K ( x , y , z , t )
o
o
ИСО,
точки
и
в начальный момент
времени совпадают, K движется
относительно K со скоростью
(u c).
r r ut ,
K
x
x
u xt ,
Y
мт
K
Y
y y u y t ,
Z
o
u
K
K.
r
r z z u z t ,
u
ut
.
t
t
X
o
X
Z
u , a a .

4.

Принцип относительности Галилея
Взаимное расположение и скорость относительного движения МТ не зависят от выбора ИСО, следовательно, и силы инвариантны относительно преобразований
Галилея:
F F.
Законы Ньютона не изменяют вид при
преобразовании координат и времени:
F ma , F12 F21 , F m a , F12 F21 .
Законы механики одинаковы во всех ИСО.

5.

Постулаты С Т О
1905г. А.Эйнштейн
В любых ИСО все физические явления
при одних и тех же условиях протекают
одинаково.
Скорость света в вакууме одинакова во
всех ИСО, не зависит от скорости
движения источника и приемника света:
м
c 3 10 .
с
8

6.

Преобразования
Лоренца
( ~ c)
Y Y
K K
o o
Z t Z
X X
x
x t
1
2
,
y y,
z z,
t
c
c
K
t x / c
1
K
2
2
скорость, измеренная в
долях скорости света.

7.

Следствия из преобразований Лоренца
1. Одновременность событий
Если в ИСО в одной точке одновременно
происходят два события, то в другой ИСО они
будут одновременными и пространственно
совпадающими.
Если события в системе K пространственно
(
t
t
),
разобщены 1
,
но
одновременны
1
2
2
то в системе K эти пространственно разобщенные
события оказываются и неодновременными :
(x x )
x1 x2 , t1 t 2 .

8.

Это следует из преобразований
Лоренца для координат и времени:
x1
t1
(t 2 t1 )
x1 t
1
2
t x1 / c
1
2
, x2
2
, t 2
x 2 t
1
2
,
t x 2 / c
1
2
2
.
может иметь разные знаки (второе
событие может предшествовать
первому ).
Но порядок следования причинно-следственных событий во всех ИСО одинаков.

9.

2.Длительность событий в разных ИСО
длительность
t 2 t1 , t 2 t1 события в K и K .
K :
2
2
t1 x / c
t 2 x / c
t1
, t 2
,
2
2
1
1
t 2 t1
2
2
1
1
Время начала и конца события в системе
часы, движущиеся относительно ИСО, идут медленнее
покоящихся часов, т.е. ход часов замедляется в СО,
относительно которой часы движутся (“парадокс
близнецов”).

10.

3. Длина тел в разных ИСО
0 x 2 x1 длина стержня, покоящегося в K .
x2 t x1 t длина стержня в K ,
K K
x
t
где
и x2 t
1
0
координаты концов
X
o
стержня в системе K :
X
Y Y
o
x1 t
x1 t
1
2
, x2 t
x2 t
1
2
.
2
2
x2 x1 1 0 1 лоренцево
сокращение продольных размеров тел.

11.

4. Пространственно – временной интервал
В четырехмерном пространстве
Эйнштейна событие характеризуется
четырьмя координатами (x, y, z, t):
c t12
12 ,
s12
2
2
2
s12 c t
2 2
12
2
12
это интервал между двумя событиями, где
12
x2 x1
2
y2 y1 z 2 z1
2
2
расстояние между точками трехмерного
пространства, в которых произошли события.
s12 inv при переходе от одной ИСО к другой.
s12

12.

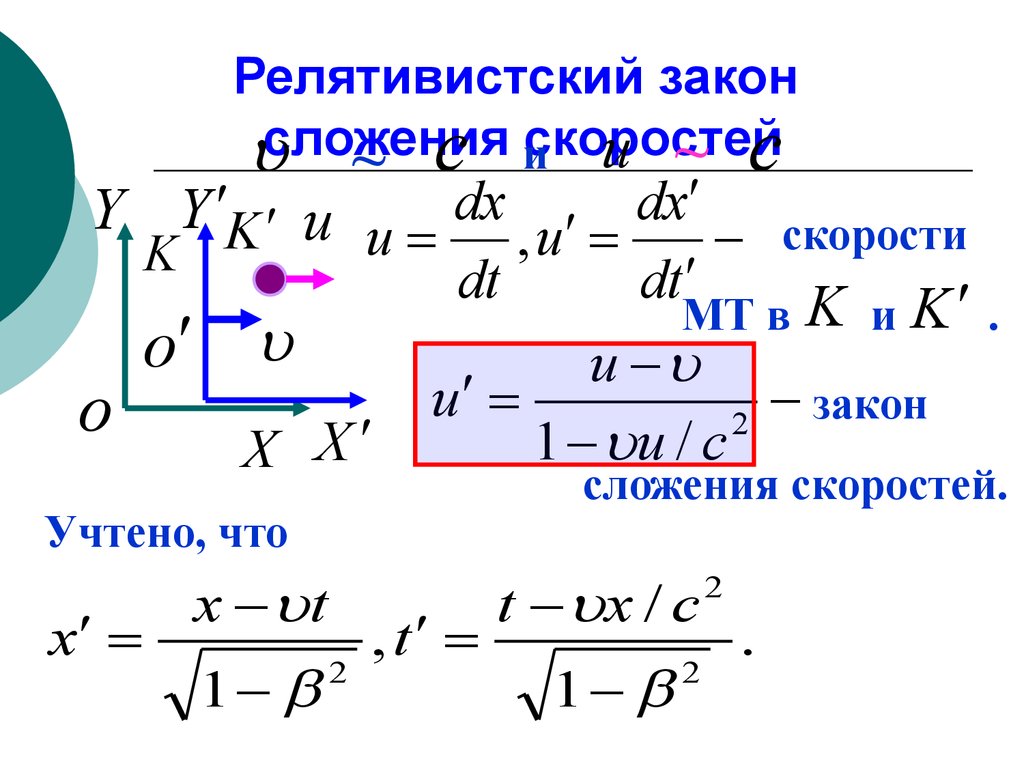
Релятивистский закон
скоростей
u ~ c
и
сложения
c
~
Y Y K u u dx , u dx скорости
K
dt
d
t
МТ в K и K .
o
u
o
X X
u
Учтено, что
x
x t
1
2
, t
1 u / c
2
закон
сложения скоростей.
t x / c
1
2
2
.

13.

Задача. Определить скорость светового сигнала,
излучаемого с космического корабля, удаляющегося от Земли со скоростью
.
u c
1) c;
2) 0,5c
u ?
u
c
c c
1)u
2
c;
2
2
1 u / c
1 c / c
c c
2
c c 0,5c c 1 0,5
2)u 2
2
c.
2
c 0,5c
c 1 0,5
2
3

14.

Релятивистская динамика
1. При
~
c масса
m
частицы
зависит от ее скорости:
m
2.
m0
m
где
0 - масса частицы в
,
2 той ИСО, относительно
1
которой частица покоится.
Импульс релятивистской частицы:
p m
m0
1
2
зависит от скорости
нелинейно.

15.

Задача. Во сколько раз увеличится масса
электрона, движущегося со скоростью
m
m0
1
m
1
2
m0
1
2
0,8c ?
,
1
2
0,8 c
1
2
c
1
1
1,67.
1 0,64 0,6
2

16.

3. Уравнение релятивистской динамики:
d m0 dp где p - импульс
F
, релятивистской
dt 1 2 dt частицы.
4. Закон сохранения релятивистского импульса
(следствие однородности
пространства):
n
mi i
i 1
1
2
const
релятивистский импульс замкнутой системы
не изменяется с течением времени.

17.

Взаимосвязь массы и энергии
1. Кинетическая энергия
d
m
0
dt
dWк A Fdr
dt 1 2
m c2
2
0
dWк d
c dm
1 2
приращение кинетической энергии частицы
пропорционально приращению ее массы.
Wк
dW
c
к
0
m
2
dm
;
W
m
m
c
к
0
m0
2

18.

2. Полная энергия системы частиц
Изменение массы частицы сопровождается
изменением ее полной энергии:
W c m.
2
Полная энергия системы равна произведению ее массы на квадрат скорости света в
2
m0 c
вакууме:
2
W mc
.
1
2
2
энергия
Или W m0 c Wк , где W0 m0 c
2
покоя.
4.
ЗСЭ
(следствие однородности времени):
полная энергия замкнутой системы сохраняется .

19.

При какой скорости ~ c энергия
частицы больше энергии покоя в 2 раза?
c
c
3
3
c
1) ;2) ;3) c;4) c;5)
2
4
4
2
2.
W mc
2
2
1
1 2
c
m0 c 2
1 2
;4 1
3
4
2
W0
1 2
1;
3
c.
2
2
;
3
;
4

20.

Если общая мощность излучения Солнца составляет 3,8 10 26 Вт, то вследствие излучения
его масса за сутки уменьшается на (кг):
1)2,8 10 ;2)3,8 10 ;3)5,2 10 ;4)8,7 10 ;5)3,6 10 .
3
9
12
16
14
W
W mc m 2 ;
c
26
3,8 10 Вт 24 3600c
14
m
3,6 10 к Г.
16
2
2
9 10 м / с
2