Similar presentations:
Логарифмическая функция
1.
2.
Изобретениелогарифмов, сократив
работу астронома,
продлило ему жизнь.
Пьер Симон Лаплас
3.
Логарифмическаяфункция
y = logax
где
a – заданное число
a > 0, a 1
4.
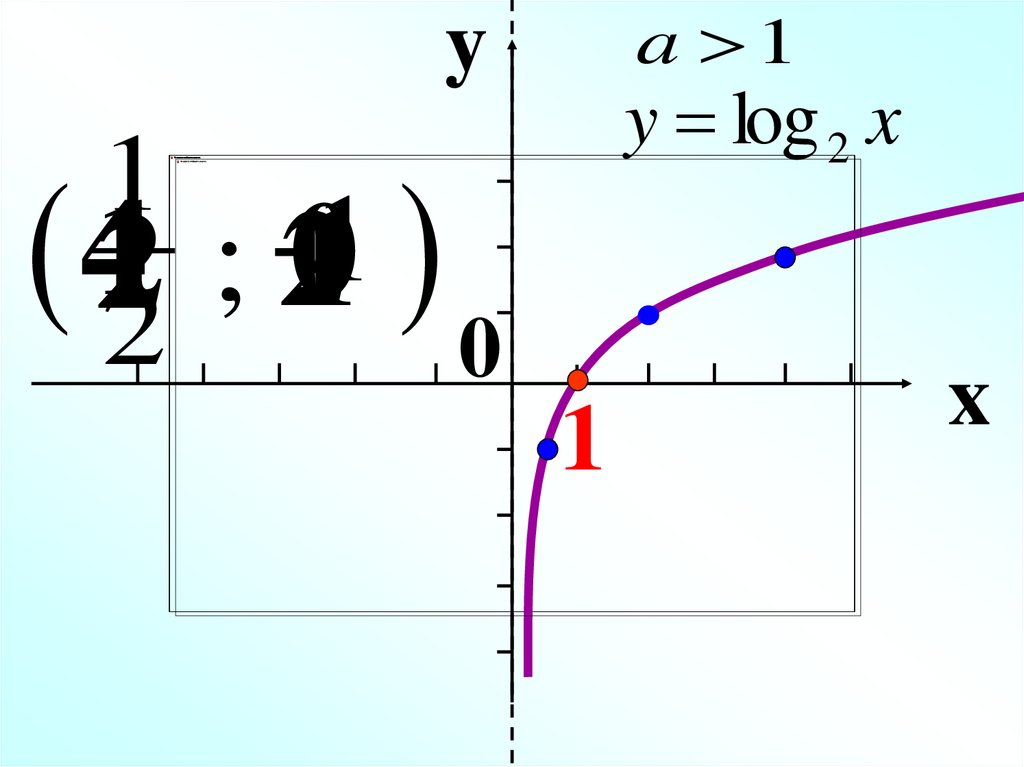
a 1y
y log 2 x
1
4122 ; -1
201
0
1
x
5.
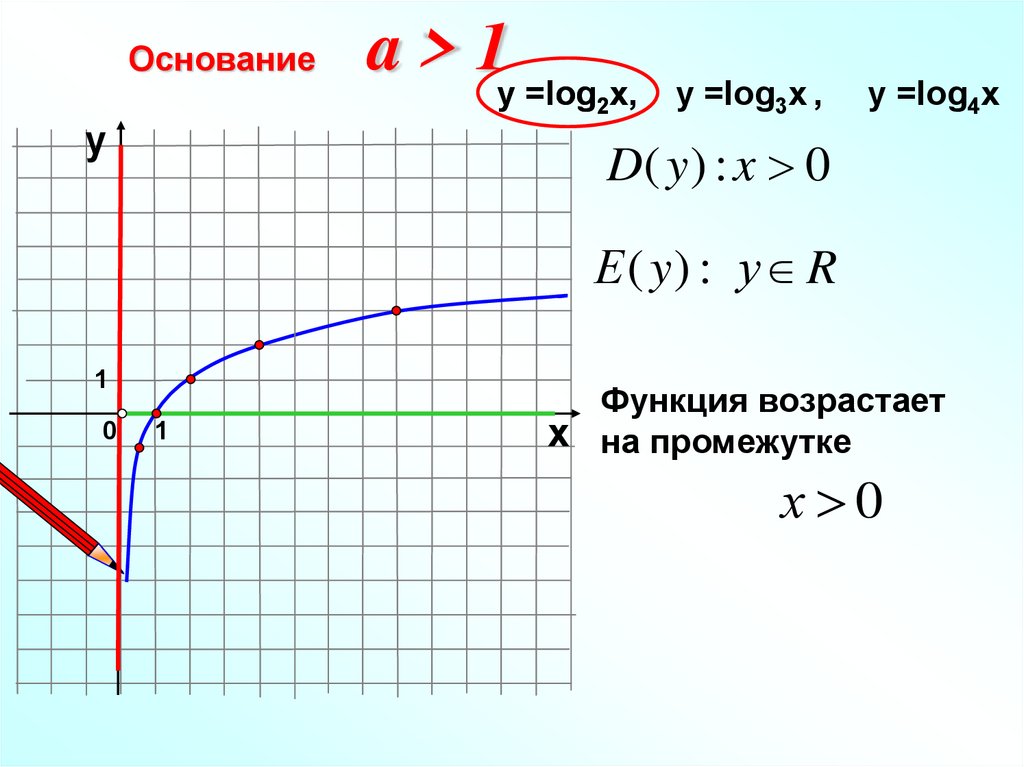
Основаниеу
a>1
у =log2x
x,
у =log3x ,
у =log4x
D( y ) : x 0
Е ( y) : у R
1
0
1
Функция возрастает
х на промежутке
х 0
6.
y log 2 x yy 0 x 1
0
1
y 0
x
x 0;1
7.
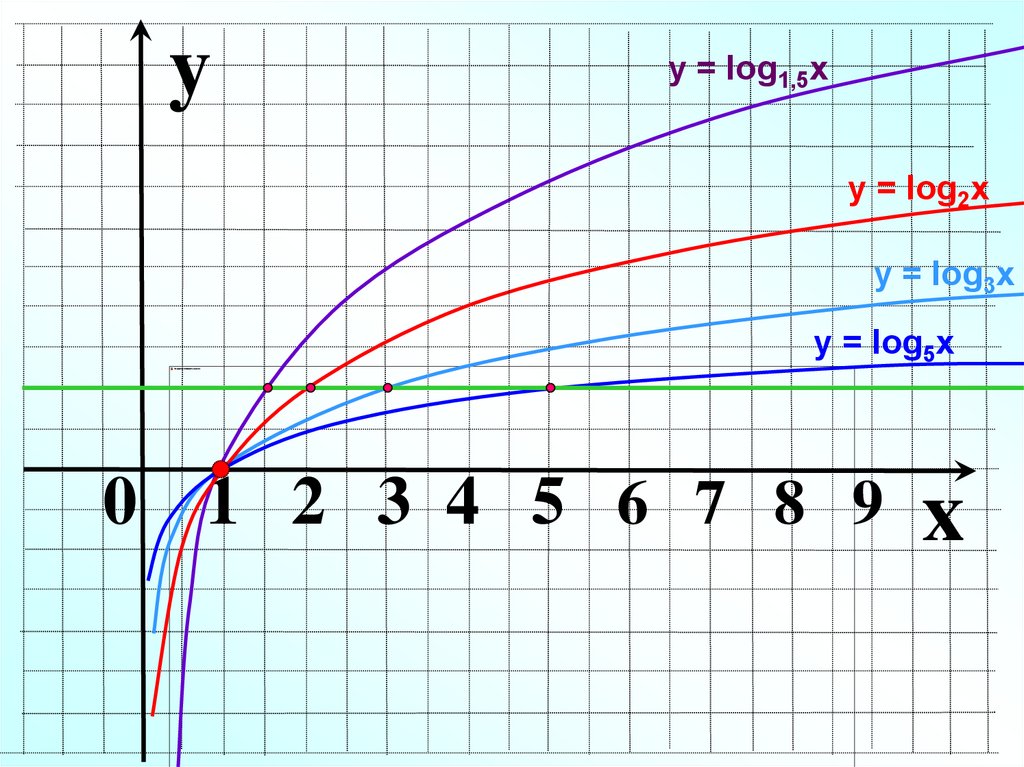
yу = log1,5x
у = log2x
у = log3x
у = log5x
0
1 2 3 4 5 6 7 8 9
x
8.
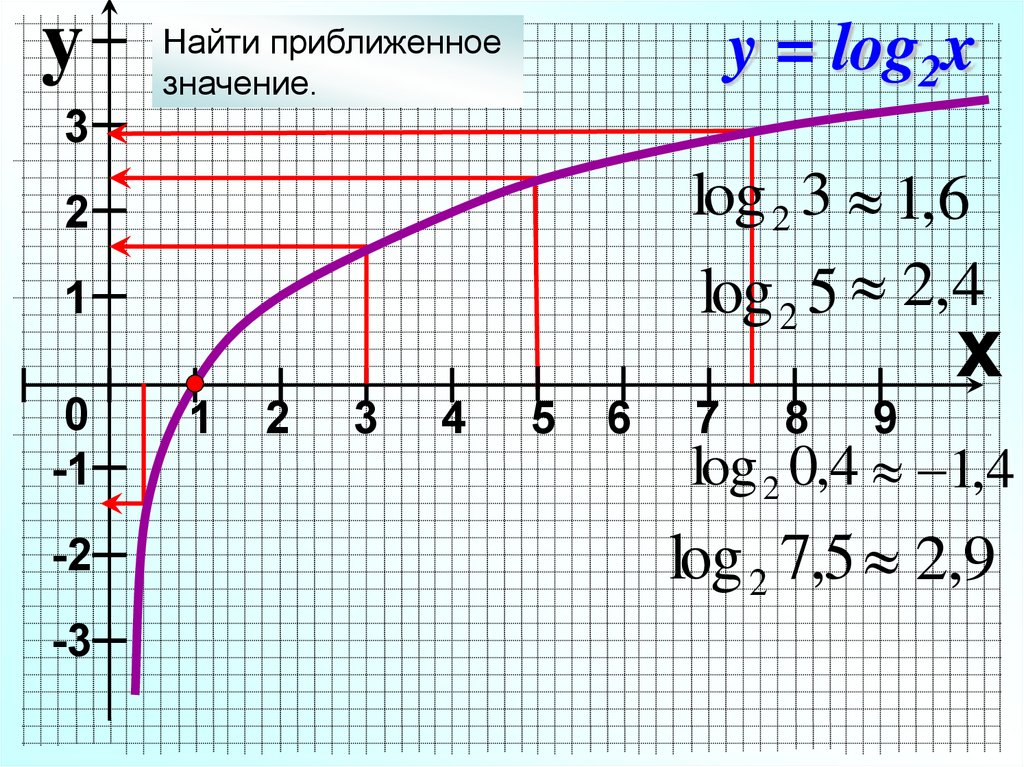
yy = log2x
Найти приближенное
значение.
3
log 2 3 1,6
log 2 5 2,4
2
1
0
-1
-2
-3
х
1
2
3
4
5
6
7
8
9
log 2 0,4 1,4
log 2 7,5 2,9
9.
y1
1
0
1422 ; -1
-2
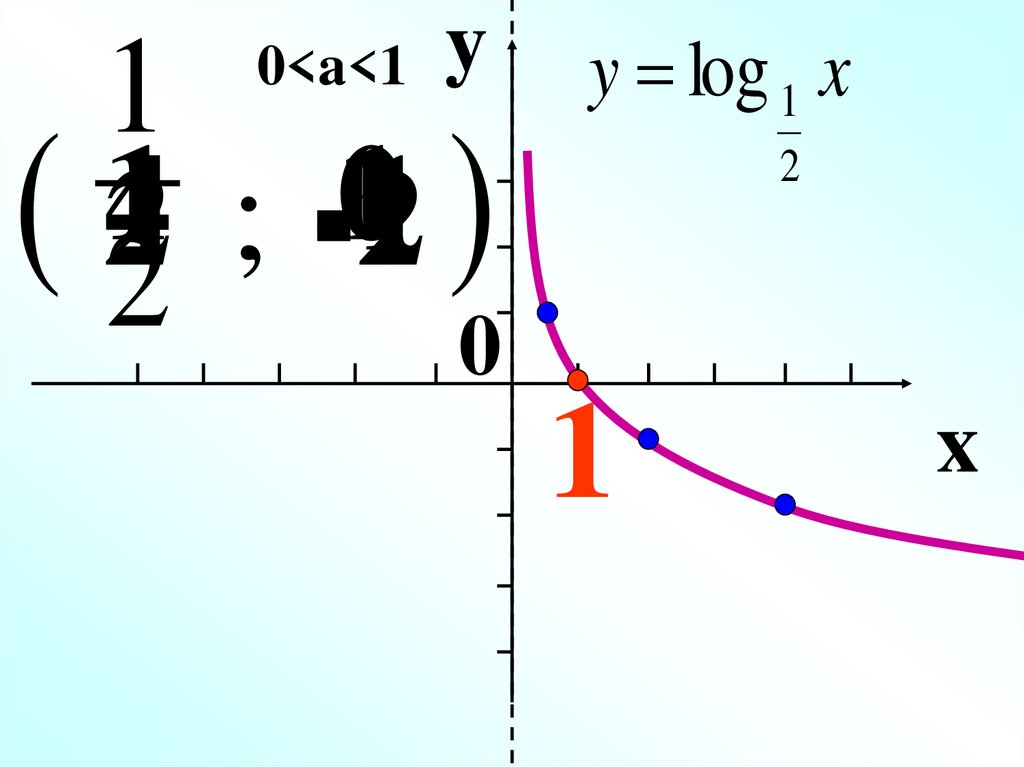
0
0<a<1
y log 1 x
2
1
x
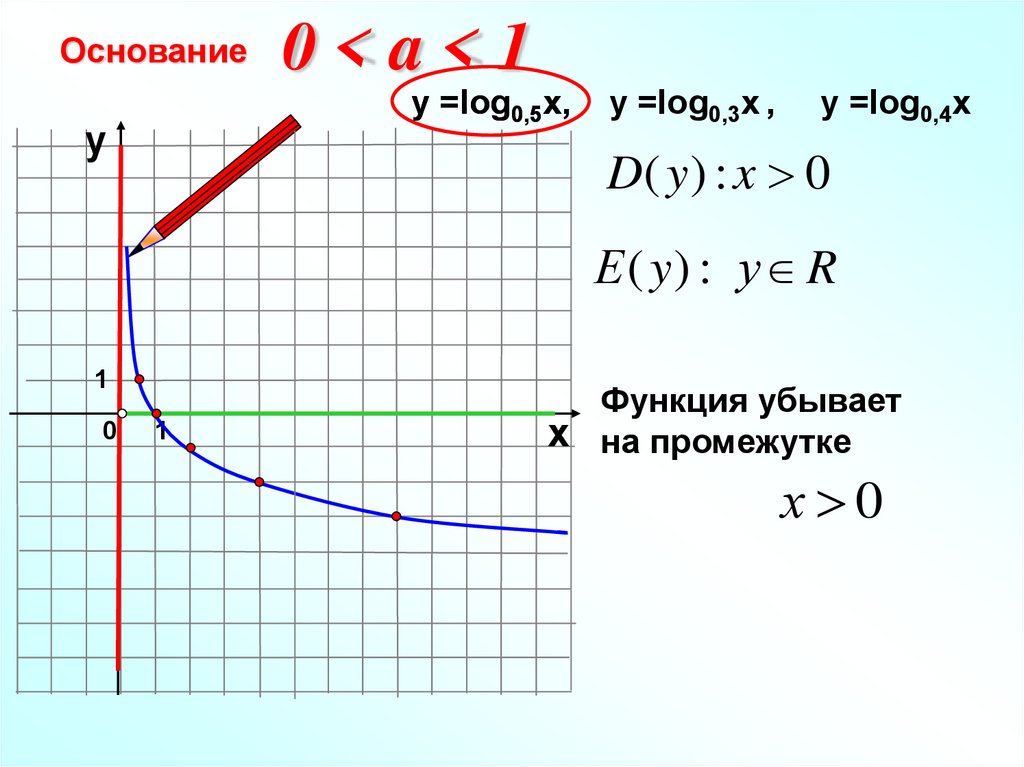
10.
Основание0<a<1
у =log0,5x
x,
у
у =log0,3x ,
у =log0,4x
D( y ) : x 0
Е ( y) : у R
1
0
1
Функция убывает
х на промежутке
х 0
11.
0<a<1y log 1 x
y
x 0;1
2
y 0
x =1
y 0
0
1
y 0
x 1
x
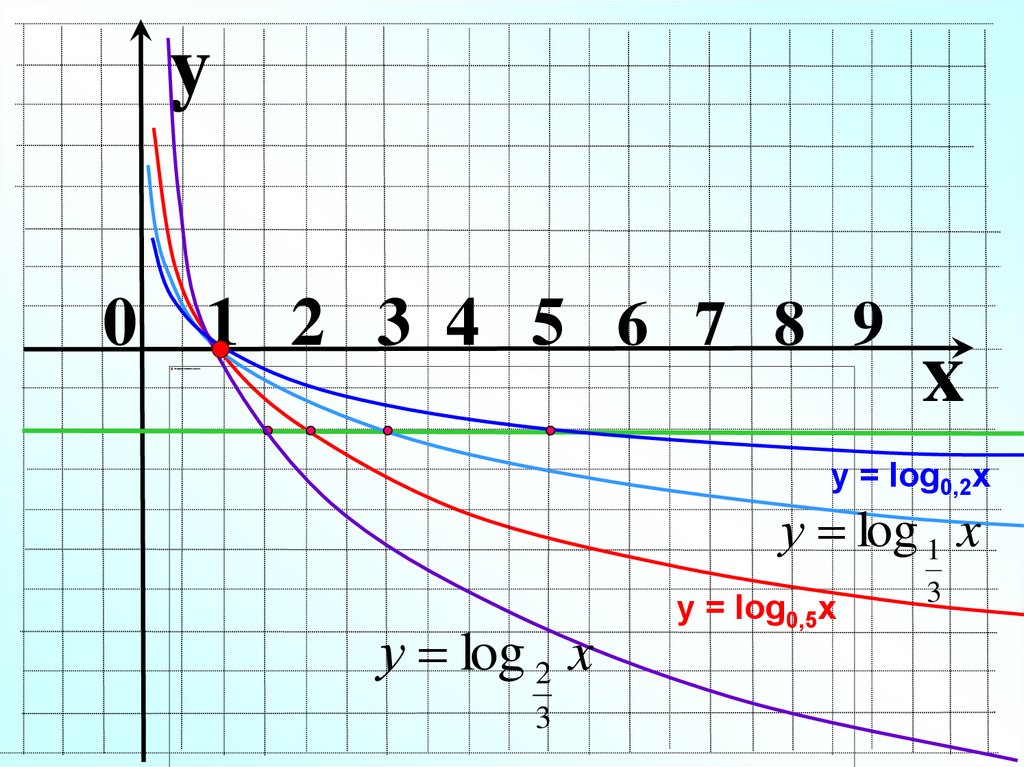
12.
y0 1 2 3 4 5 6 7 8 9
x
у = log0,2x
у log 1 x
у log 2 x
3
у = log0,5x
3
13.
y = logaxу
у
х
0
1
a>1
0
1
0<a<1
х
14.
Сравнение чисел можно выполнить, используя свойствовозрастания или убывания логарифмической функции
log32,7 < log34 т.к. функция у = log3x возраст.
*
log 116 *
< log 1 9
3
т. к. функция у log 1 x убыв.
3
3
log 2 4,6 > log
0 21
*
функция у = log2x возраст.
15.
log 3 > log1 33
*
функция у = log3x возраст.
log 1 23 *
< log
0 11 т. к. функция у log
3
log 1
3
1
3
x убыв.
3
1 т. к. функция у log x убыв.
1 1
3 < log
1
3
3
3
*
16.
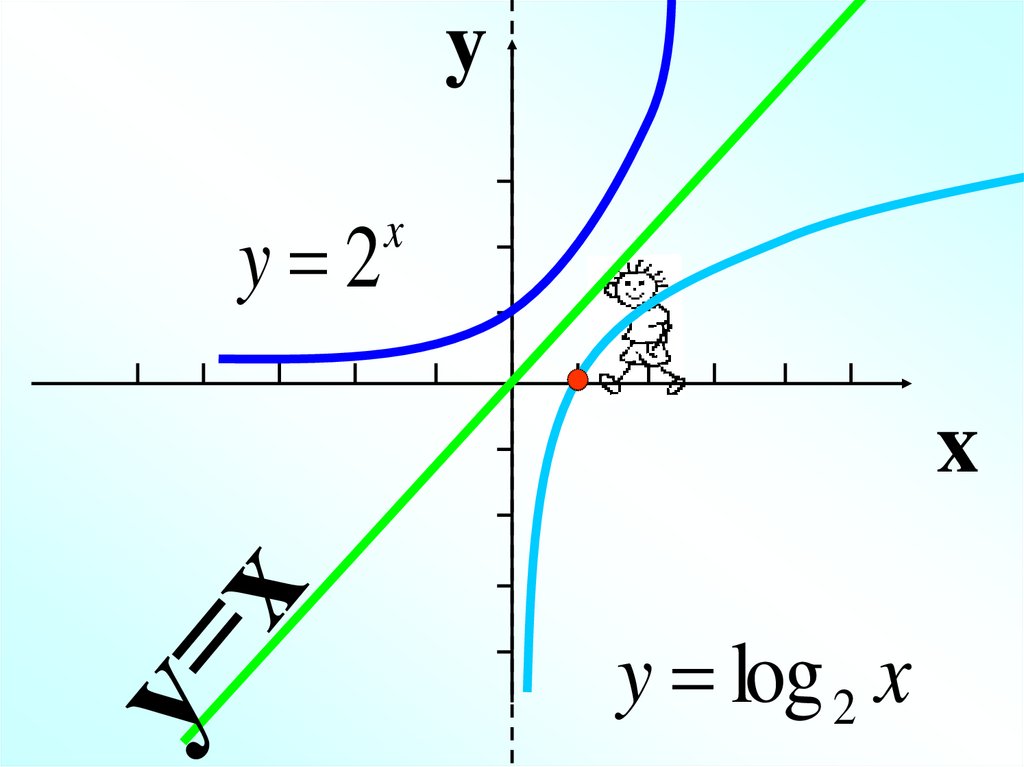
yy 2
x
x
y log 2 x
17.
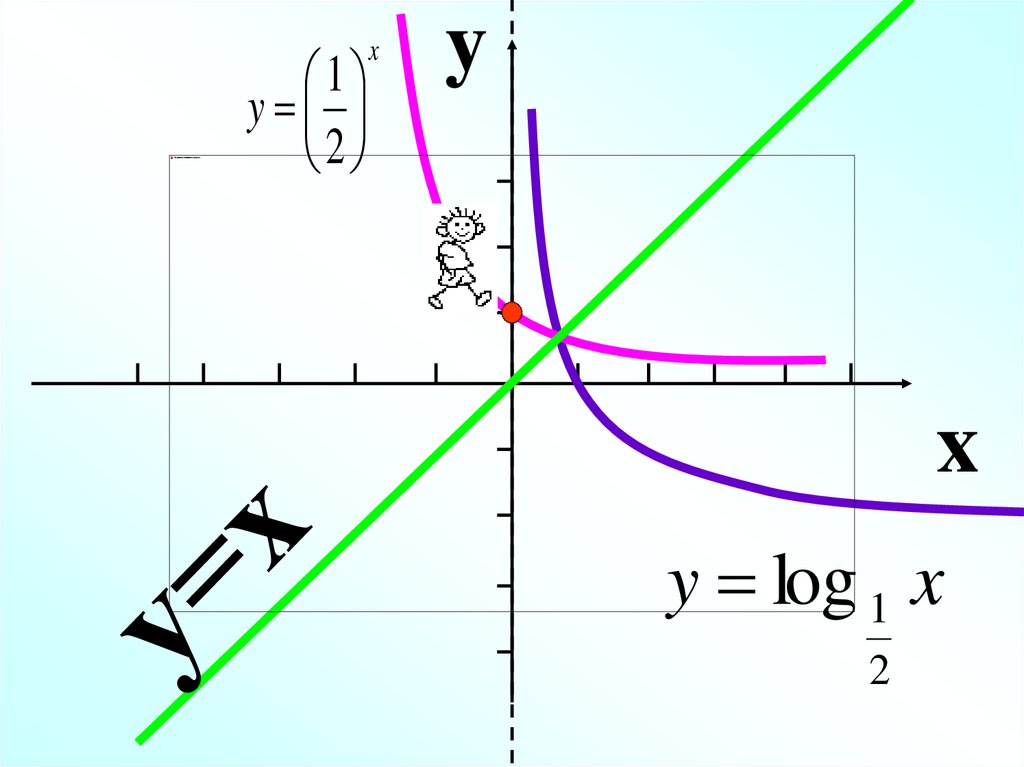
1y
2
x
y
x
y log 1 x
2
18.
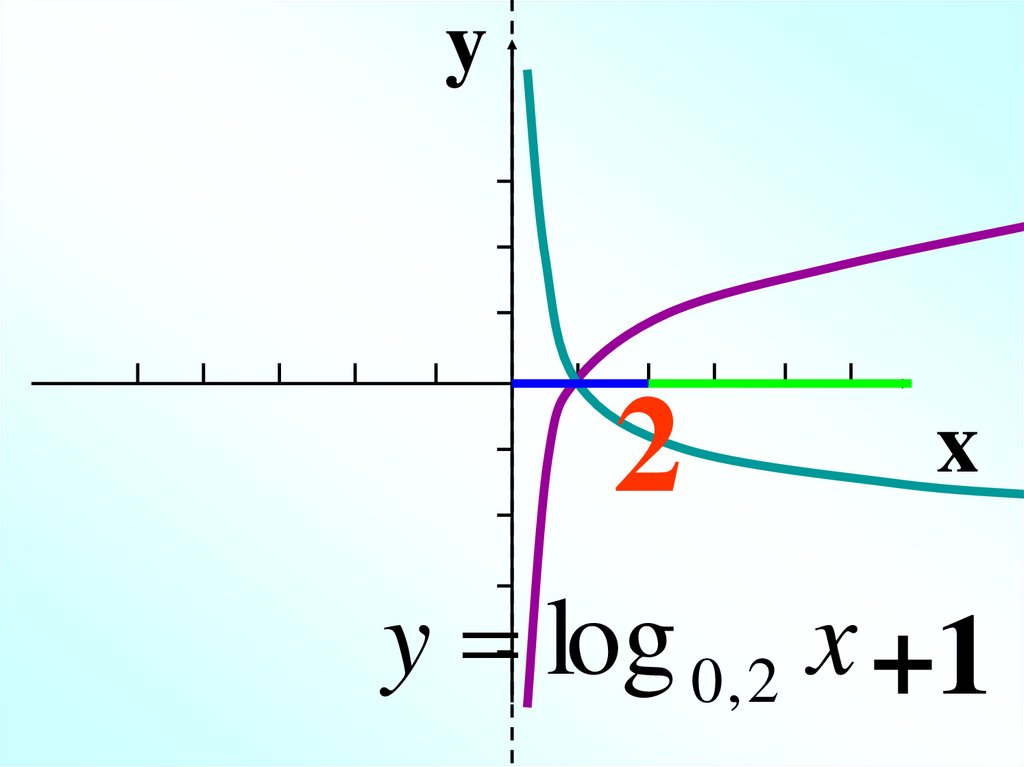
y2
x
y log 0, 2 x +1
19.
y-2
x
y log 2 x 3
20.
Используя графики функций решить уравнениеlog2x = - x+1
у
у log 2 x;
у x 1.
1
0
1
х
х 1
21.
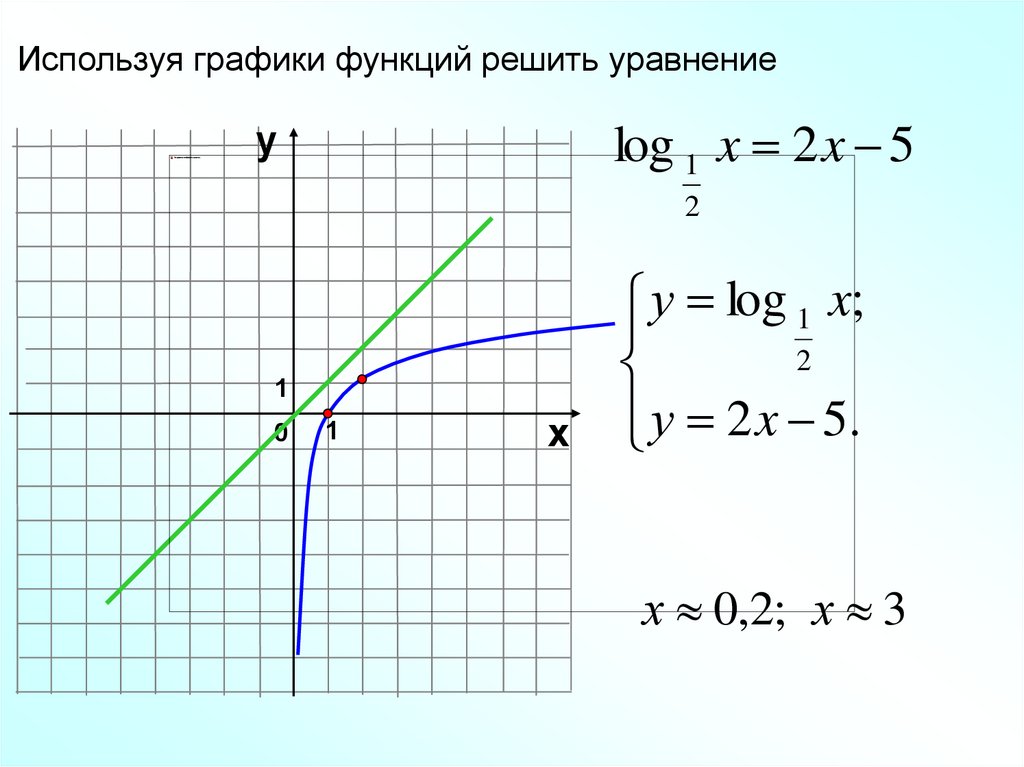
Используя графики функций решить уравнениеlog 1 x 2 x 5
у
2
1
0
1
х
у log 1 x;
2
у 2 x 5.
х 0,2; х 3
22.
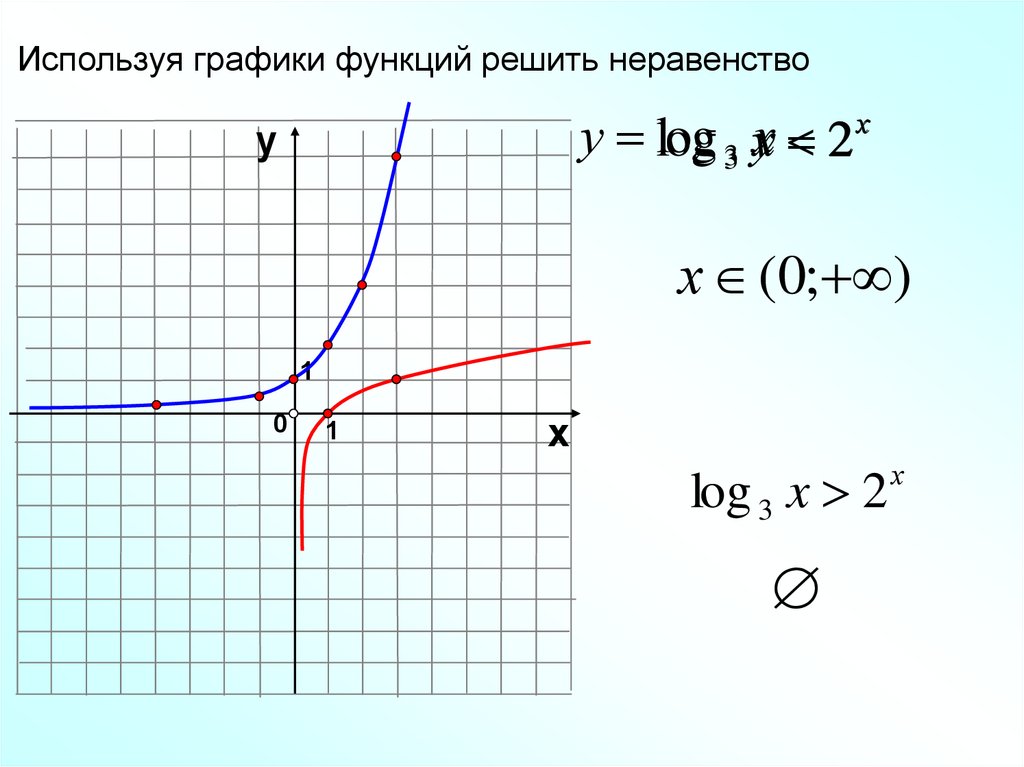
Используя графики функций решить неравенствоу log 3 уx
2
у
х
х (0; )
1
0
1
х
log 3 x 2
х
23.
Используя графики функций решить неравенствоу
log 2 ( x 3) х
у х
у х
1
0
1
х
х ( 3; 1)
24.
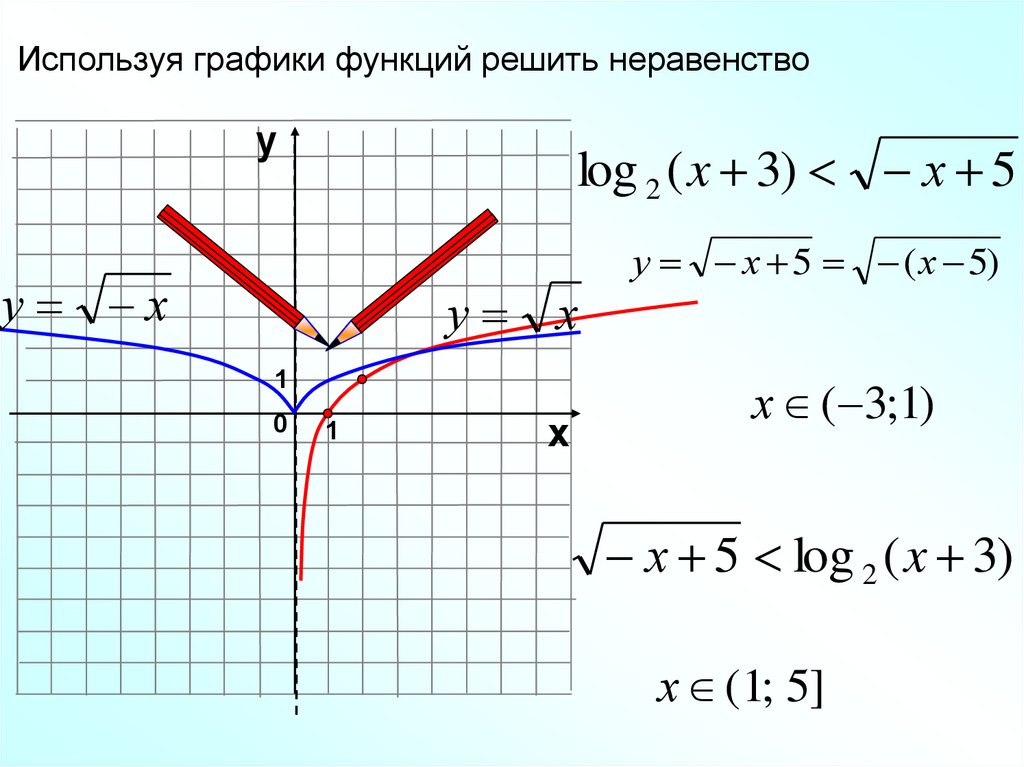
Используя графики функций решить неравенствоу
log 2 ( x 3) х 5
у х
у х
1
0
1
х
у х 5 ( х 5)
х ( 3;1)
х 5 log 2 ( x 3)
х (1; 5]
25.
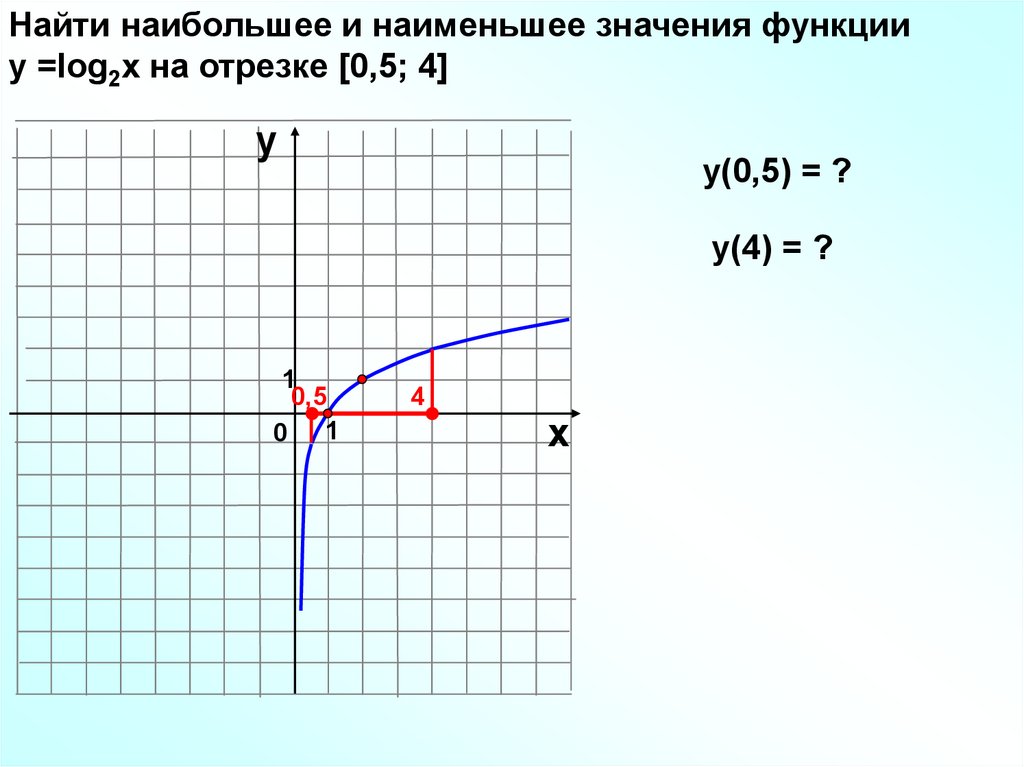
Найти наибольшее и наименьшее значения функцииу =log2x на отрезке [0,5; 4]
у
y(0,5) = ?
у(4) = ?
1
0,5
0 1
4
х




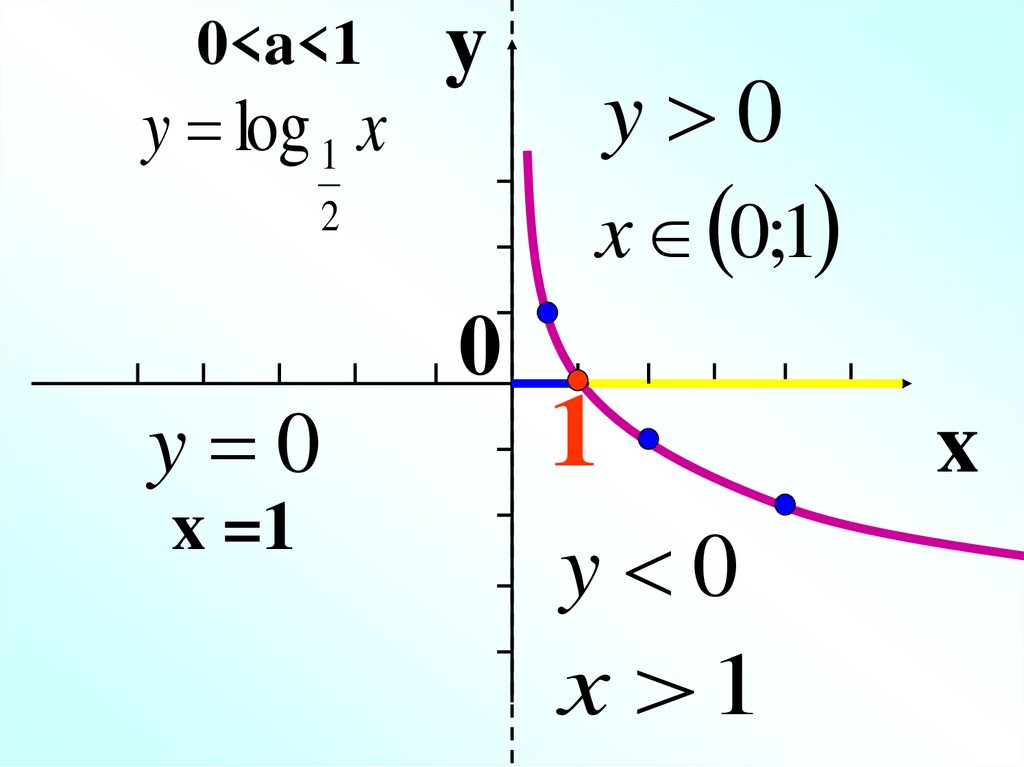



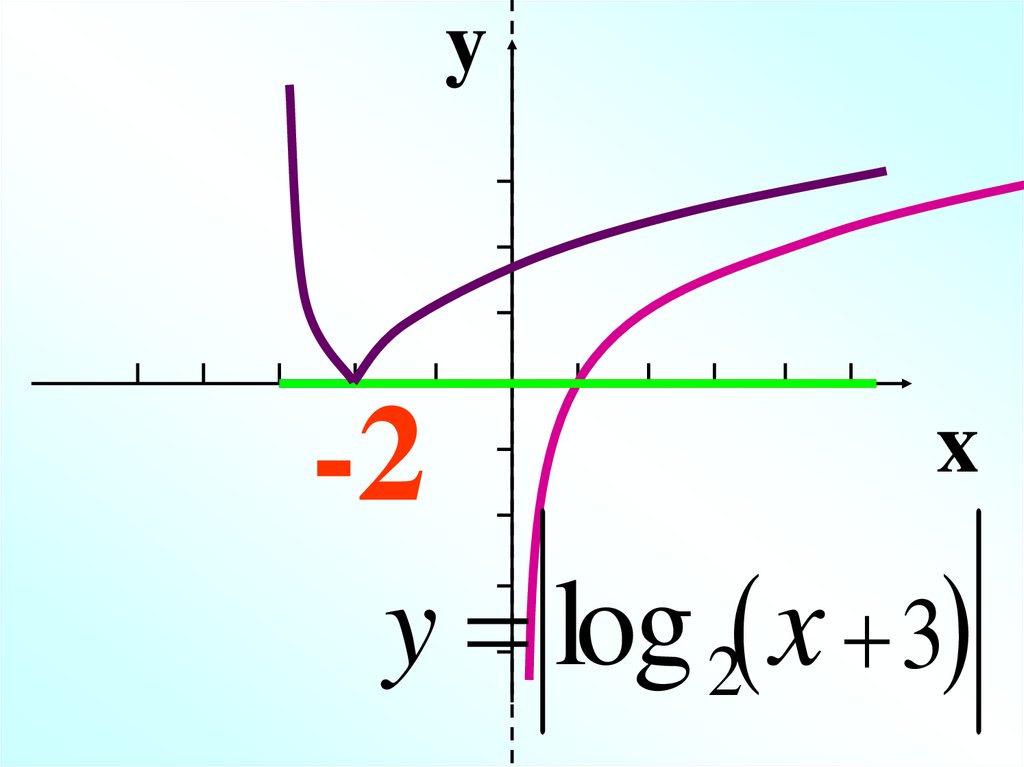


 mathematics
mathematics








