Similar presentations:
Логарифмические неравенства
1. Логарифмические неравенства
2.
Приизучении логарифмических
функций рассматриваются
неравенства вида:
logax < b
logax ≥ b
3.
logax > logayx>0; y>0
1)
2)
eсли а>0, то x>y
eсли 0<a<1, то x<y
4. Решить неравенство
log 3(x+2)<3log0,5(2x+1)>-2
log3(x-2)>1
log2(x-3)>5
lg(x-3)≥2
lg(x-1)≤0
5.
log2x>1log3x>2
log5x≥0
log0,5x≥0
log2x≤1
log3x<2
log2x<1/2
log3x<0
:
6. Закрепление
log 4 x 1 Log 4 x log 4 2Log
1
26
26 x 2 0.
Log16 x Log16 x 15 1.


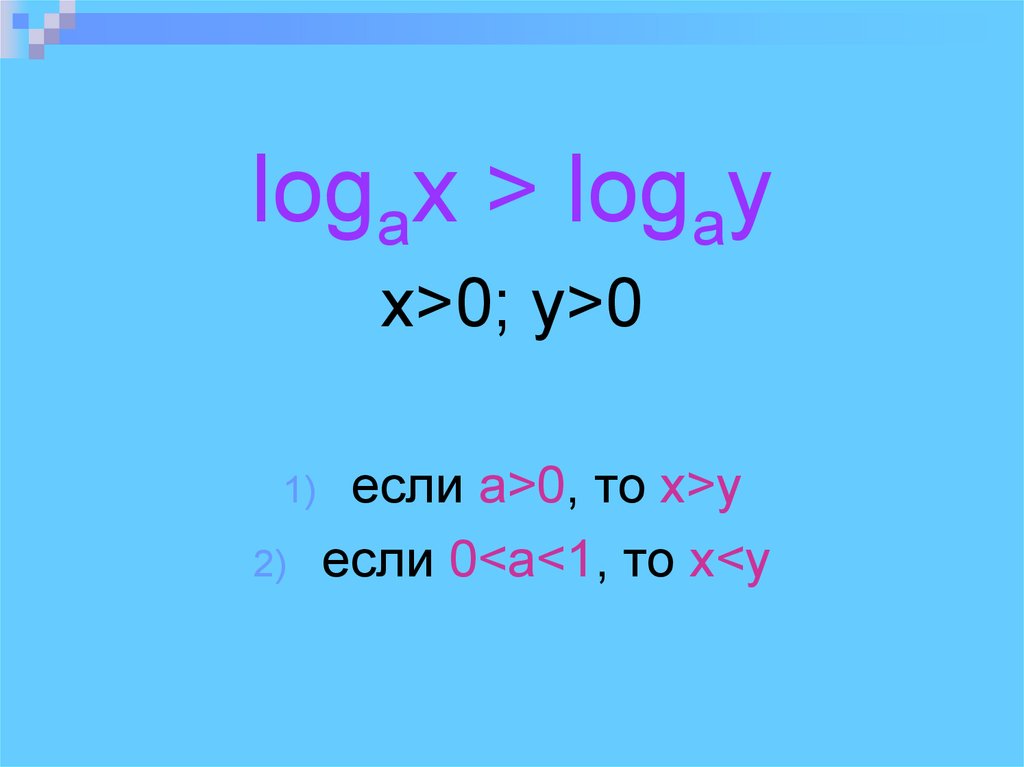



 mathematics
mathematics








