Логарифмическая функция. График и свойства. Понятие логарифмической функции

1.

y log a x
Подготовила: Коровашкова А.Д.
учитель математики

2. Тема урока: Логарифмическая функция. График и свойства.

3.

Цель урока:
- Ввести понятие логарифмической функции
- График логарифмической функции
- Изучить основные свойства

4.

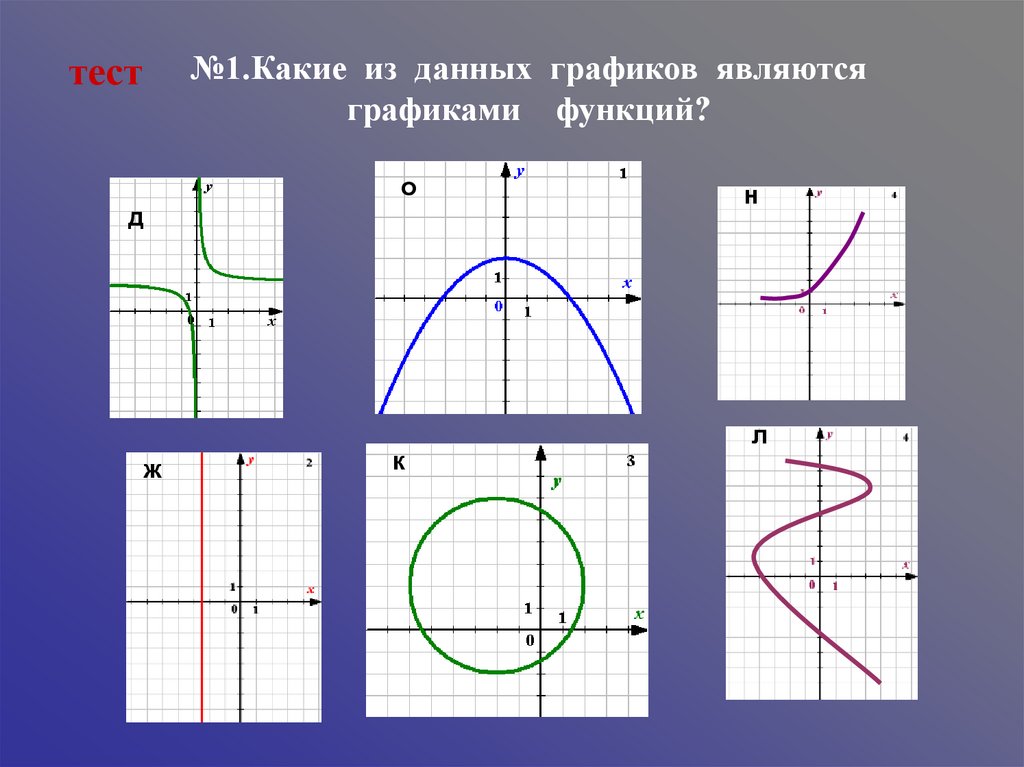
№1.Какие из данных графиков являются
графиками функций?
тест
о
д
ж
к
н
л

5.

• Решить уравнение:
3х 6
• Л)2
Н) log3 6
• П)log6 3
А)нет решений

6.

1. На одном из рисунков изображен график
функции .
Укажите
y букву
5 x этого
1
рисунка.
К)
О)
К
)
Е)
Ц)

7.

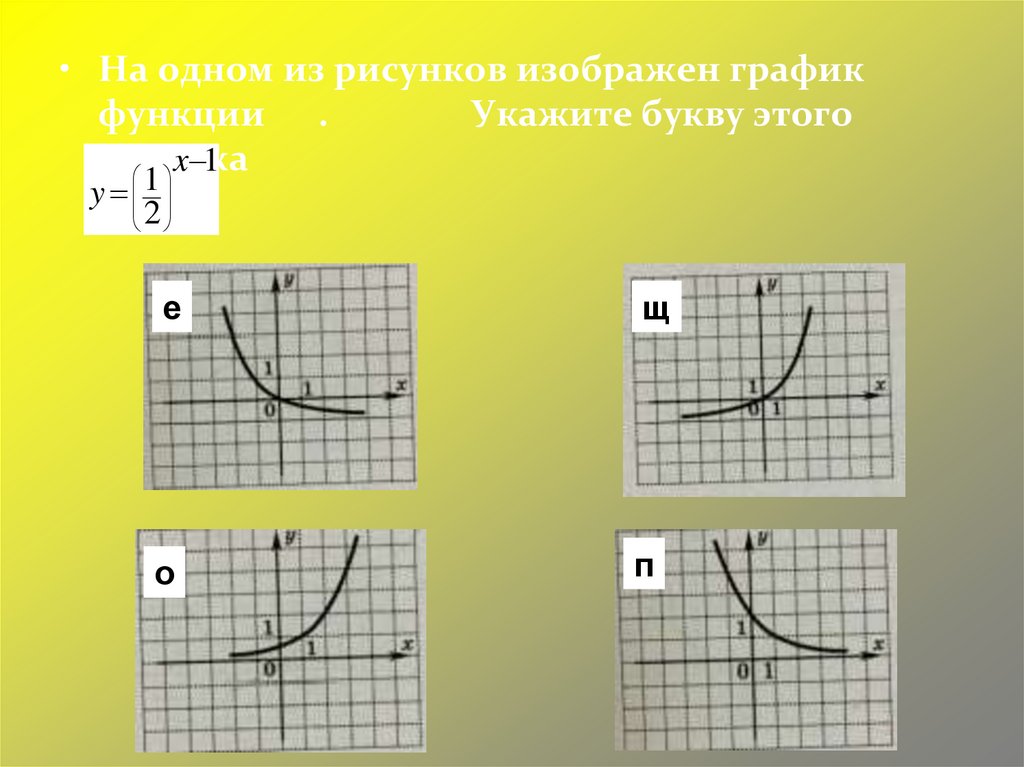
• На одном из рисунков изображен график
функции .
Укажите букву этого
рисунка
x 1
y 1
2
е
щ
о
п

8.

Ц)
Е)
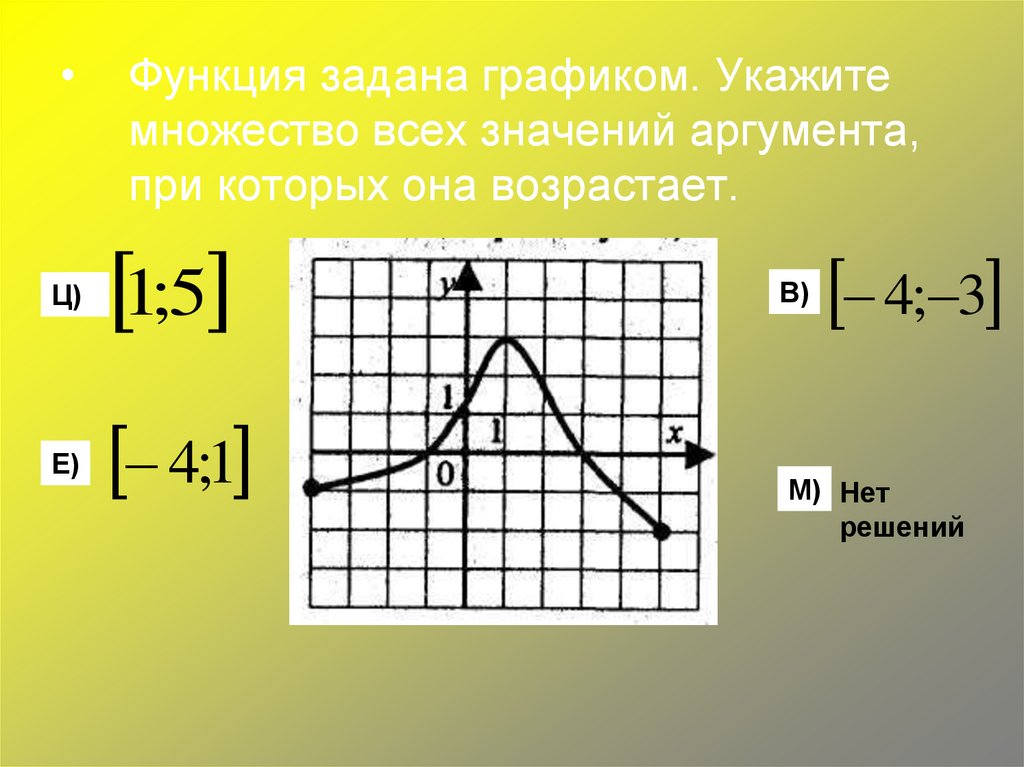
Функция задана графиком. Укажите
множество всех значений аргумента,
при которых она возрастает.
1;5
4;1
В)
4; 3
М) Нет
решений

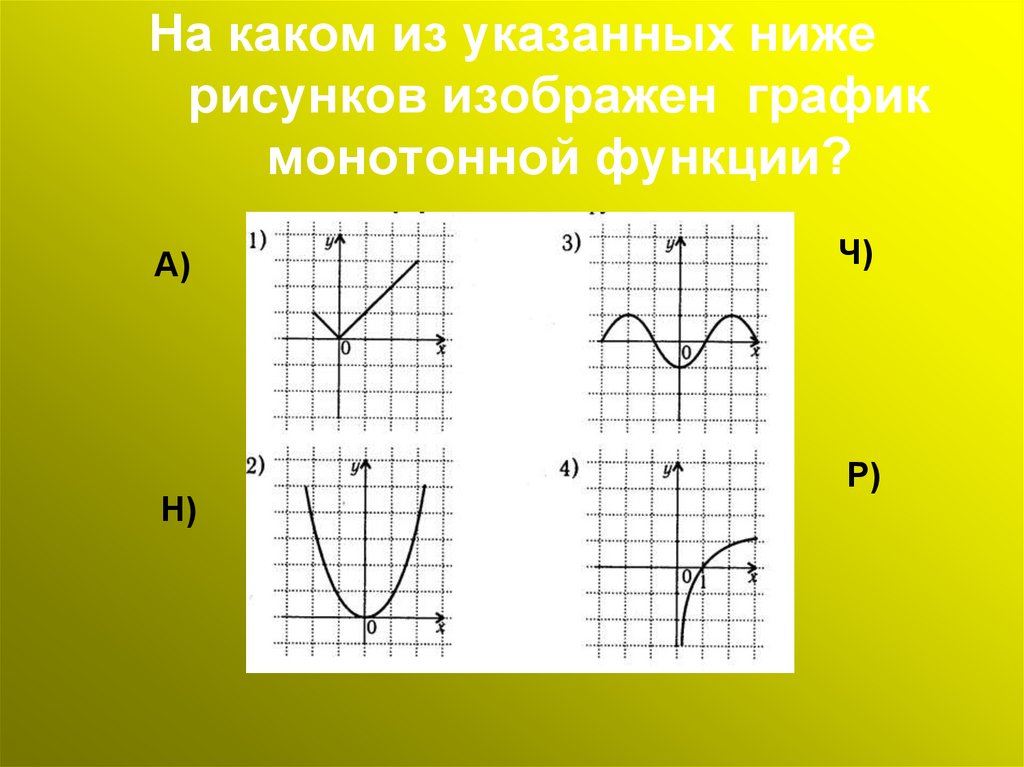
9. На каком из указанных ниже рисунков изображен график монотонной функции?

А)
Н)
Ч)
Р)

10. Джон Непер

(1550 г.— 4 апреля 1617г.)
Шотландский математик изобретатель логарифмов.
В 1590-х годах пришел к идее
логарифмических вычислений
и составил первые таблицы
логарифмов, однако свой
знаменитый труд “Описание
удивительных таблиц
логарифмов” опубликовал
лишь в 1614 году.
Ему принадлежит определение
логарифмов, объяснение их
свойств, таблицы логарифмов
синусов, косинусов, тангенсов
и приложения логарифмов в
сферической тригонометрии.

11.

Y= а х
X=log a y
Y=log a x
Показатель степени
Функция y=Log aX
Где а>o, а ≠ 1
называется
логарифмической

12. Так как показательная функция y= (где a>0,a=/1)является монотонной (при a>1 возрастающей и при 0<a<1 убывающей), то она имеет

ах
Так как показательная функция y=
(где a>0,a=/1)является монотонной
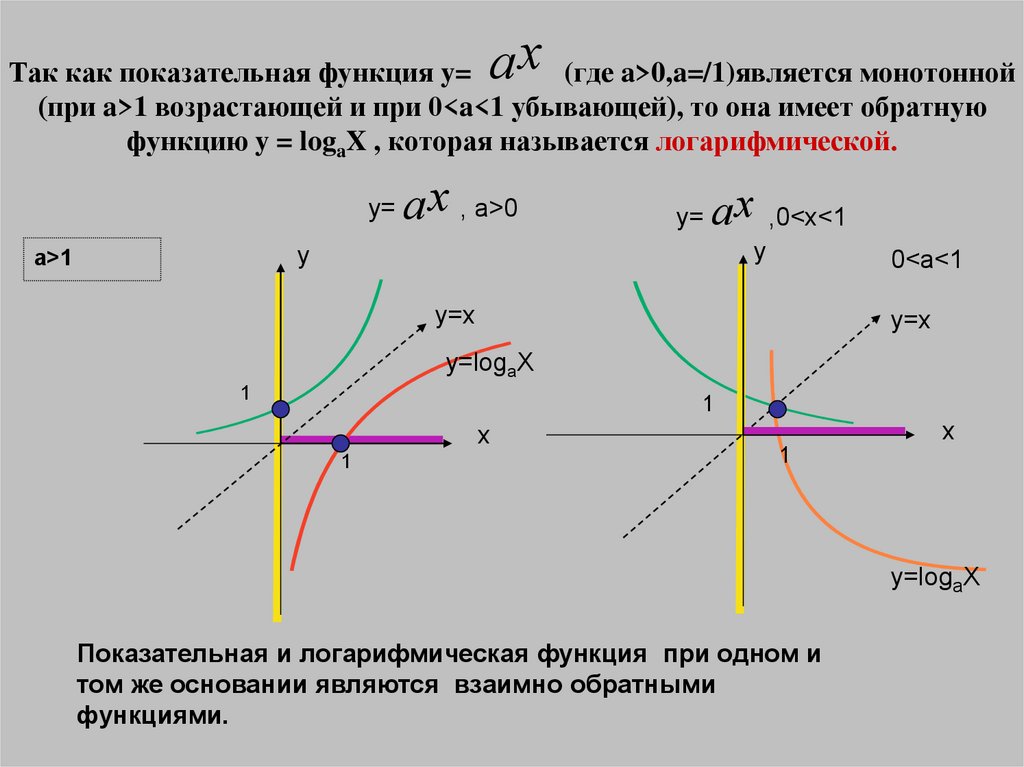
(при a>1 возрастающей и при 0<a<1 убывающей), то она имеет обратную
функцию y = logaX , которая называется логарифмической.
y=
а х , a>0
y=
ах
y
y
a>1
,0<x<1
0<a<1
y=x
y=x
y=logaX
1
1
x
1
x
1
y=logaX
Показательная и логарифмическая функция при одном и
том же основании являются взаимно обратными
функциями.

13. Свойства функции.

1.Область определения- Множество всех положительных чисел(x>0)
2.Множество значений-Множество всех действительных чисел
3.График функции проходит через точку- (1;0)
4.На промежутке x>0 функция является
Возрастающей
убывающей
5.Функция принимает положительные значения(y>0)
Х>1
6.Функция принимает отрицательные значения(y<0)
0<x<1
0<x<1
x>1
y
y
y log a x
y log a x
1
0
1
0
1
a 1
1
0 a 1

14.

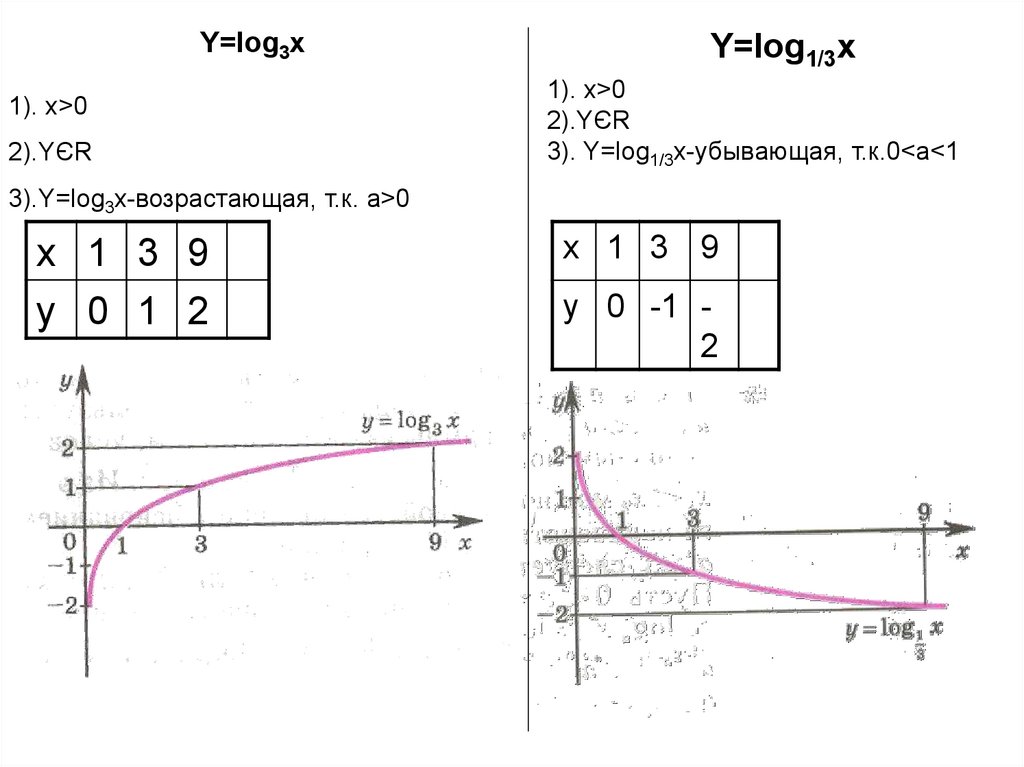
Y=log3x
1). x>0
2).YЄR
Y=log1/3x
1). x>0
2).YЄR
3). Y=log1/3x-убывающая, т.к.0<a<1
3).Y=log3x-возрастающая, т.к. а>0
x 1 3 9
y 0 1 2
x 1 3 9
y 0 -1 2

15.

y
y
y log a x
y log a x
1
1
0
1
0
x
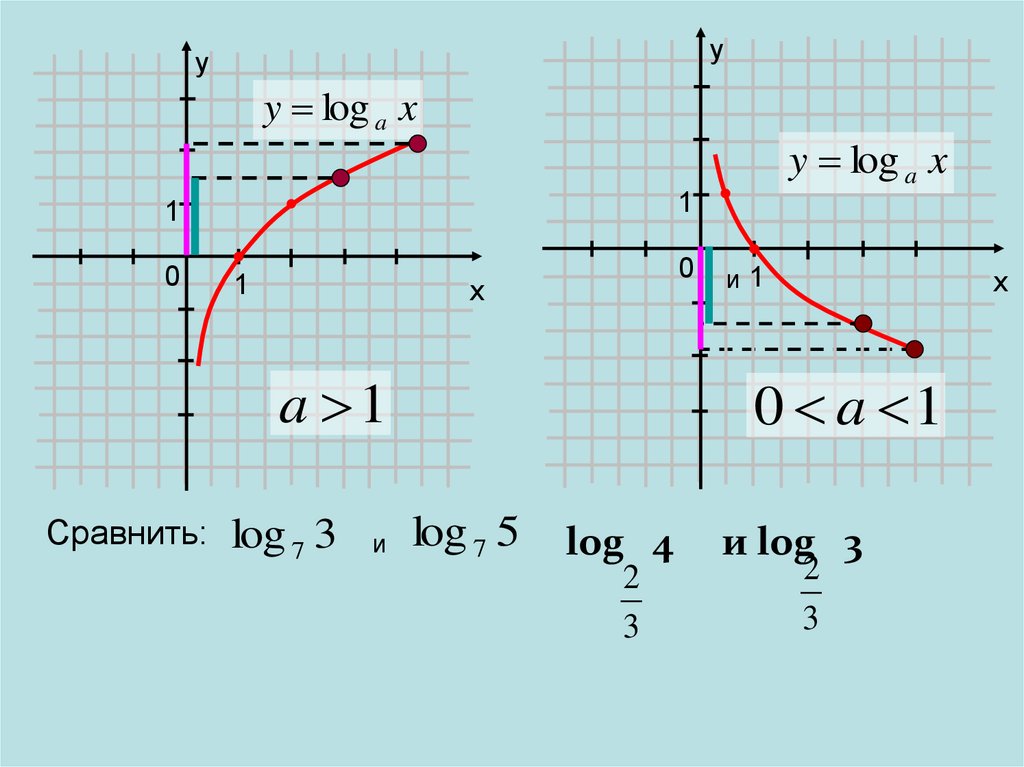
a 1
Сравнить:
log 7 3
и
и1
x
0 a 1
log 7 5
log 4
2
3
и log 3
2
3

16. Выяснить положительное или отрицательное число

Выяснить положительное или
y
y
отрицательное
число
y=log3X
y=log1/3 X
1
Log3 4,5 >0
x
1
Log 1 2 <0
3
Log3 0,45 <0
Log
1
3
0,5
>0
x

17. Построение графиков логарифмической функции

Построить график функции y= log3(x-2)
y=log3(x-2)
1
1
2
График получается
Параллельным переносом
Кривой y=log3 X
Вдоль оси X на 2 единицы
вправо
3
Область определения
Данной функции –это
множество
(2;+∞)
y=log3 X

18.

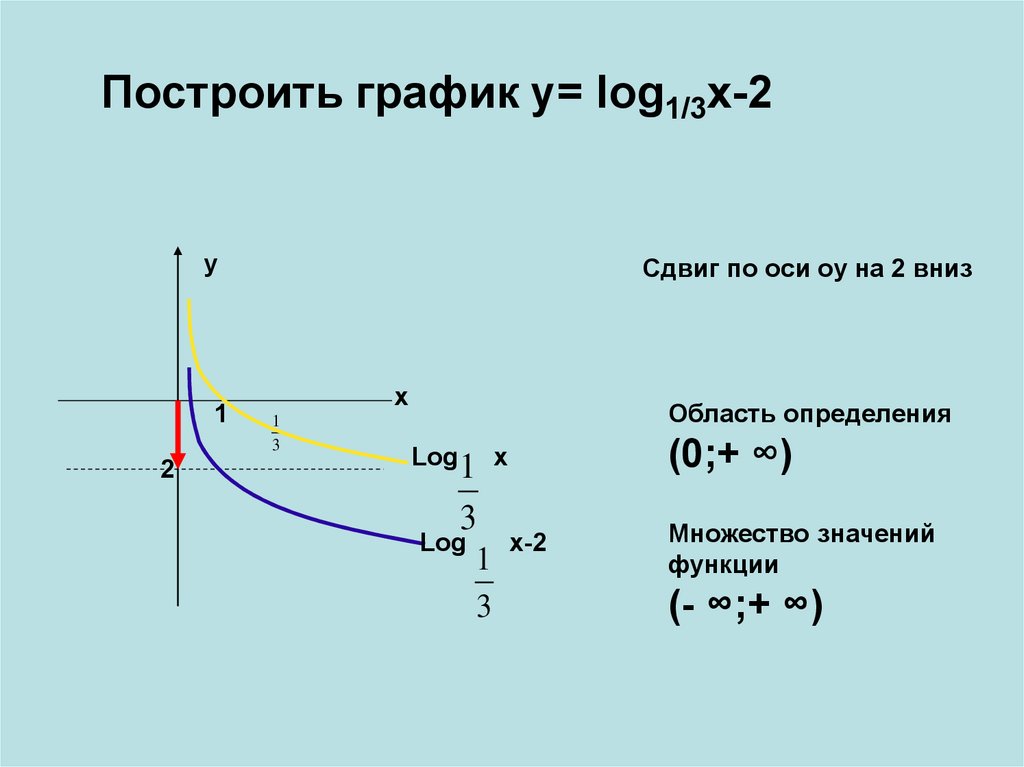
Построить график y= log1/3x-2
Сдвиг по оси оу на 2 вниз
y
1
2
x
1
3
Область определения
(0;+ ∞)
Log 1 x
3
Log
1
3
x-2
Множество значений
функции
(- ∞;+ ∞)

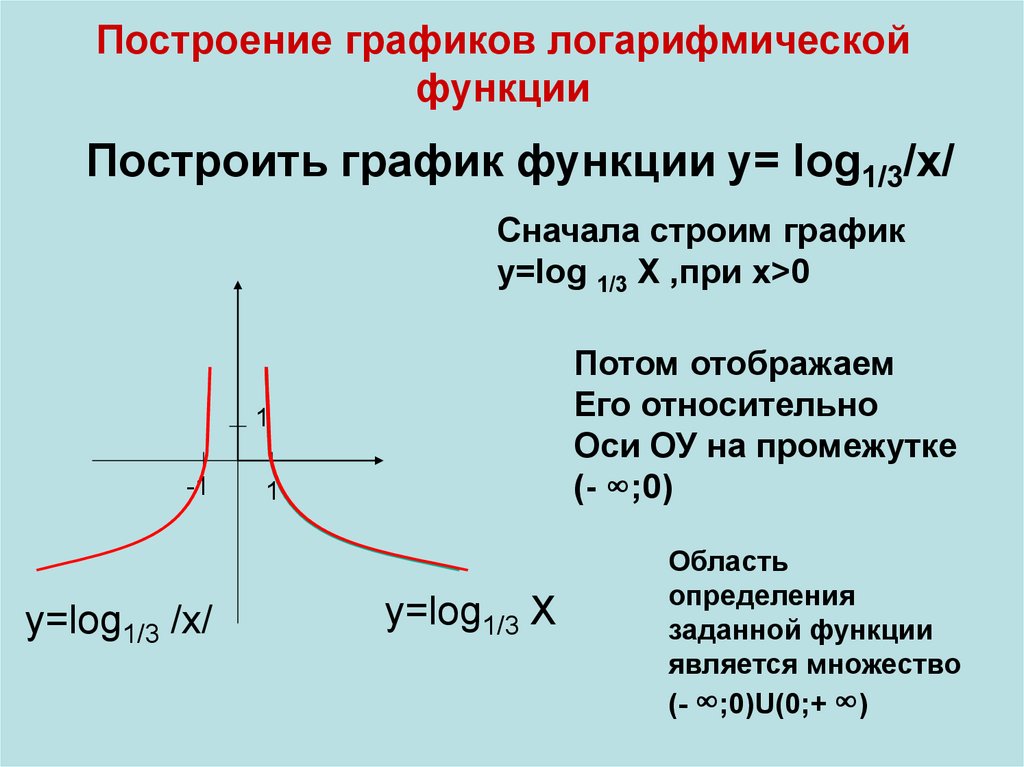
19. Построение графиков логарифмической функции

Построить график функции y= log1/3/x/
Cначала строим график
y=log 1/3 X ,при x>0
Потом отображаем
Его относительно
Оси ОУ на промежутке
(- ∞;0)
1
-1
y=log1/3 /x/
1
y=log1/3 X
Область
определения
заданной функции
является множество
(- ∞;0)U(0;+ ∞)

20.

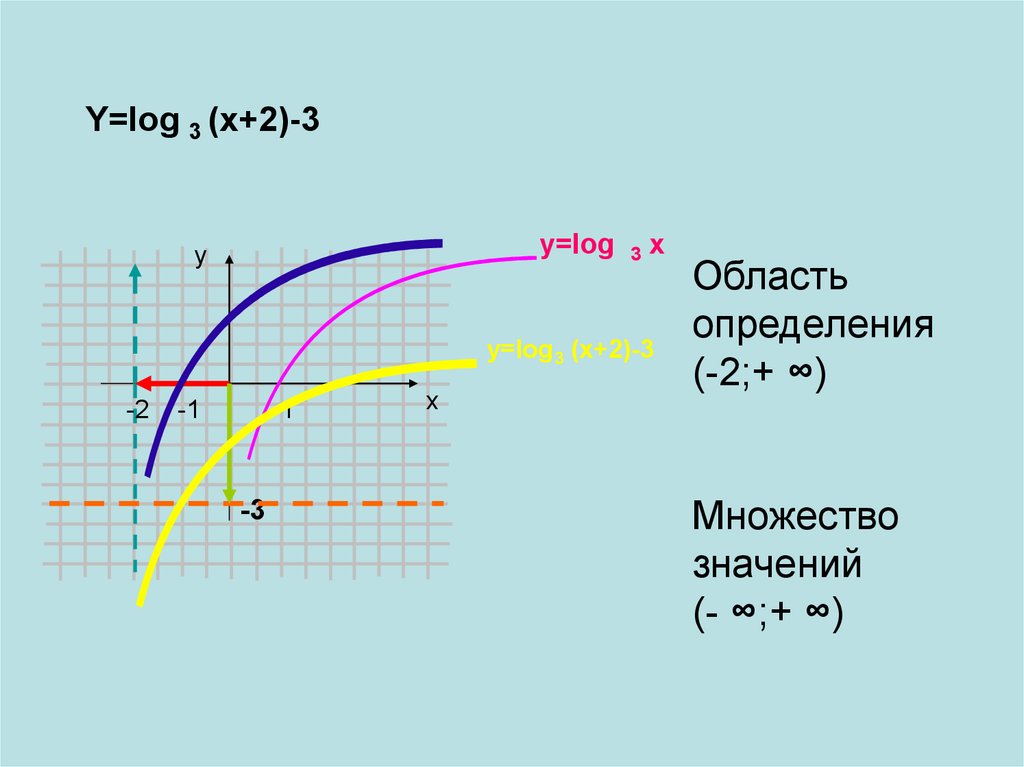
Y=log 3 (x+2)-3
y=log
y
3
x
y=log3 (x+2)-3
-2
-1
1
-3
x
Область
определения
(-2;+ ∞)
Множество
значений
(- ∞;+ ∞)

21.

Логарифмическая функция определена при
любом х
нет
Областью значений логарифмической
функции является любое действительное
число
Функция y=log5 x
является возрастающей
да
График функции пересекается с осью Ох
Существует логарифм отрицательного числа
да
да
нет

22.

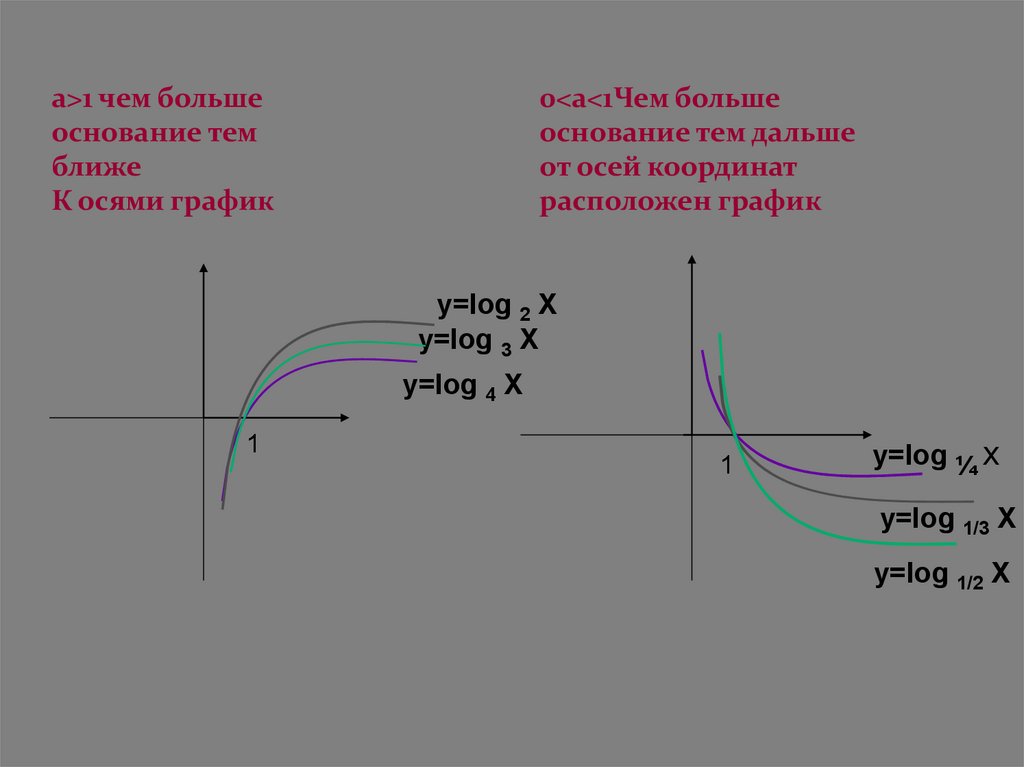
a>1 чем больше
основание тем
ближе
К осями график
0<a<1Чем больше
основание тем дальше
от осей координат
расположен график
y=log 2 X
y=log 3 X
y=log 4 X
1
1
y=log ¼ x
y=log 1/3 X
y=log 1/2 X

23.

• Какое из указанных ниже
чисел не принадлежит
области определения
Log5(36-x2)
А) 1
Н)0
Х) 5
Р) -8