Similar presentations:
Область определения и множество значений функции
1. Область определения и множество значений функции
2. Объяснение нового материала (учебник стр. 65-66).
Для области определения функции у=f(х)удобно использовать обозначение D(f).
Примеры.
1) Для функции у=х³-7х, многочлен х³-7х
имеет смысл при любом х, поэтому
D(f)=( -∞;+ ∞).
2) Для функции у=√х, подкоренное
выражение х≥0 имеем D(f)=[0;+ ∞).
3) Для функции у=1/х, знаменатель х ≠ 0
имеем D(f)≠0.
3. Работа с формулой
Задание. Найти область определенияфункции: а) у=√х+4; б) у=5 /х+4;
в) у=5 / √х+4.
Решение. а) х+4 ≥ 0. Ответ: D(f)=[-4;+ ∞) или
х ≥ -4.
б) х+4 ≠ 0. Ответ: D(f)=( -∞; -4)U( -4;+ ∞) или
D(f) ≠ -4 или х ≠ -4 .
в) х+4 > 0, что следует из пунктов а) и б).
Ответ: D(f)=( -4;+ ∞) или х > -4.
4.
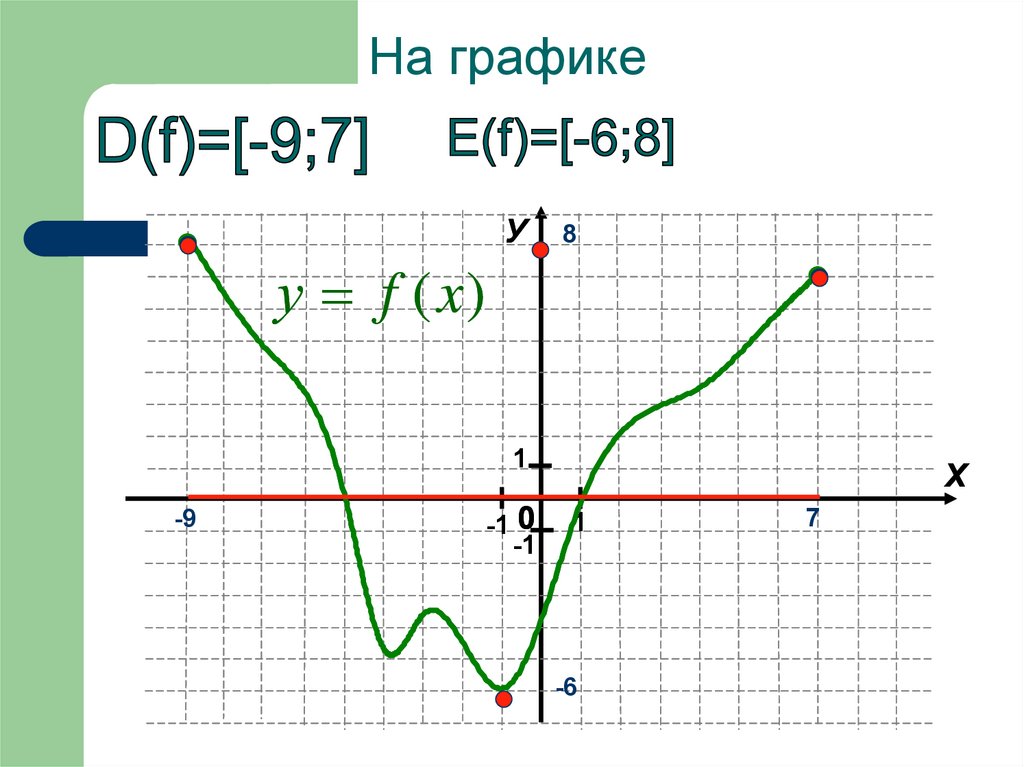
5. На графике
У8
у f (x )
1
-9
-1
0
-1
Х
1
-6
7




 mathematics
mathematics








