Similar presentations:
Определение производной
1.
Определение производнойПусть функция y = f(x) определена в некотором интервале (a; b).
Аргументу x придадим некоторое приращение
x x (a; b )
x :
Найдем соответствующее приращение функции:
y f ( x x ) f ( x )
y
Если существует предел
f(x+ Δx )
y
f(x )
0
x
х
x+Δx
х
y
lim
x 0
x
то его называют производной
функции y = f(x) и
обозначают одним из
символов:
y ;
f ( x );
dy
dx
2.
Определение производнойИтак, по определению:
f ( x x ) f ( x )
y lim
x 0
x
Функция y = f(x) , имеющая производную в каждой точке интервала
(a; b), называется дифференцируемой в этом интервале;
операция нахождения производной функции называется
дифференцированием.
Значение производно функции y = f(x) в точке x0 обозначается
одним из символов:
y ( x 0 );
f ( x 0 );
y x
0
Если функция y = f(x) описывает какой – либо физический процесс,
то f ’(x) есть скорость протекания этого процесса – физический
смысл производной.
3.
'C =0
'
x =1
¿
¿
¿
4.
'(sinx \{) =cosx
'
(cosx \{) =−sinx
1
( tgx \{) =
2
cos x
'
1
(ctgx \{) =− 2
sin x
'
5.
¿¿
¿
′
'
u u ⋅v − u ⋅v
=
2
v
v
()
'
6.
75
3
1 ¿ f (x )=3 x +5 x − 2 x + 4 x −6
Решение
'
6
4
2
f ( x)=3⋅ 7x +5⋅ 5 x +2⋅ 3 x +4⋅1 − 0
'
6
4
2
f ( x)=21 x +25 x −6 x +4
7.
62 ¿ f ( x )=(5 sin x − x )
Решение
'
f ( x)=¿
¿
8.
3¿ f ( x)=12 x− tg (x)Решение
'
'
f ( x)=12⋅ ( x ) −¿
1
f ( x)=12⋅ 1- 2
cos x
'
1
f ( x)=12- 2
cos x
'



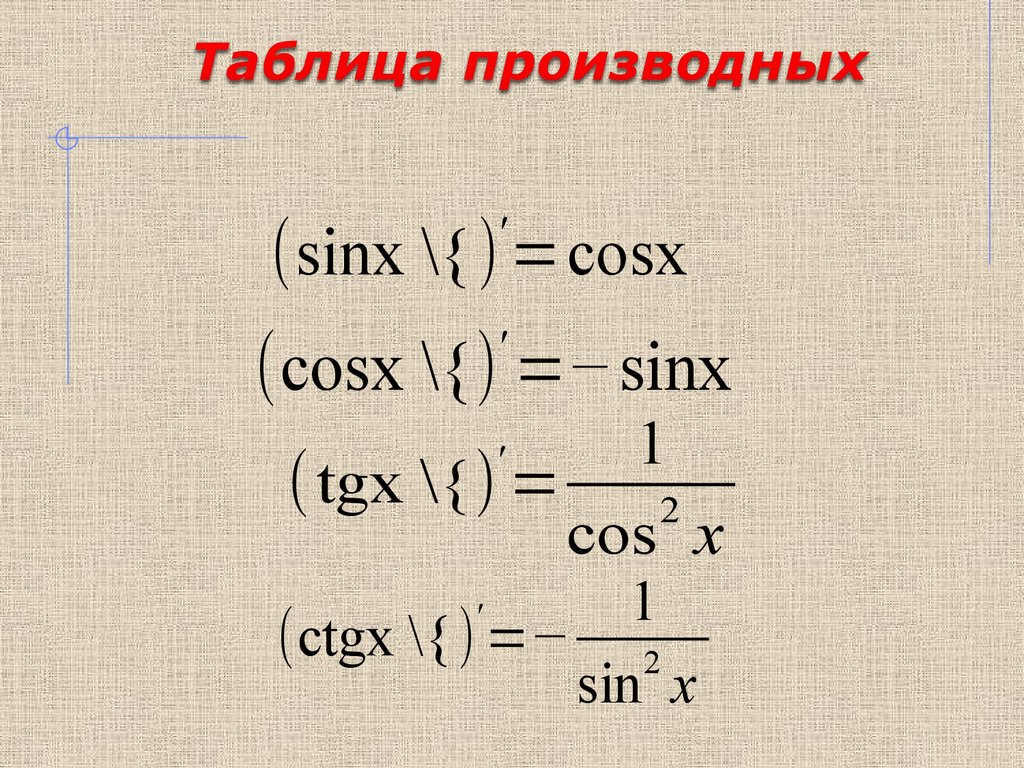


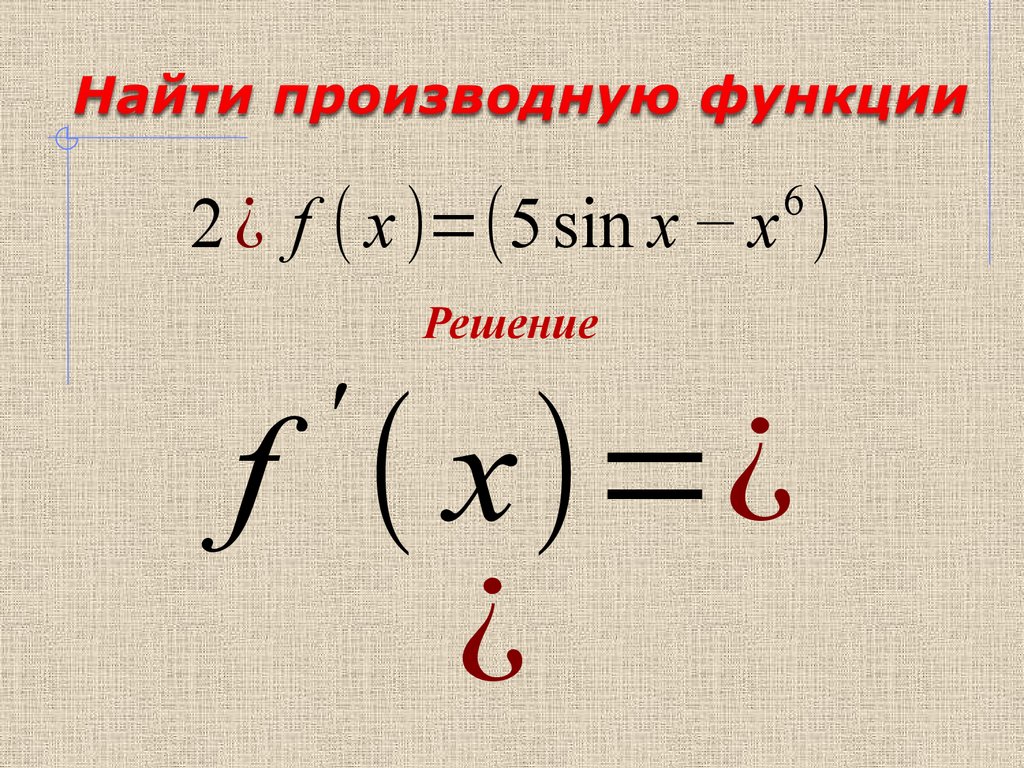

 mathematics
mathematics








