Similar presentations:
Определение производной. Правила вычисления производных. Уроки 90-91
1. Уроки 90-91.
Тема: Определениепроизводной. Правила
вычисления производных
2.
Цели обучения:10.4.1.16 - знать определения приращения
аргумента и приращения функции;
10.4.1.17 - знать определение производной
функции и находить производную функции по
определению
•10.3.1.10 - находить производные постоянной
функции и степенной функции;
•10.3.1.11 - знать и применять правила
дифференцирования
3. Критерии оценивания
• Знает определение производной• Умеет находить производную по
определению
• Знает таблицу простейших
производных
• Знает и применяет правила нахождения
производных (правила
дифференцирования)
4.
Определение производнойу
Если разностное отношение х имеет предел
при х 0 ,то его называют производной функции
в т. х0
lim
х 0
y
x
lim
x 0
f ( x0 x) f ( x0 )
f ( x 0 )
x
Вообще данную операцию называют
дифференцированием функции, а
производная – это результат
дифференцирования
5.
Пример:f ( x ) ( x ) и найти f ( x 0 ),
если x 0 3
2
1) y ( x0 x) x0 x0 2 x0 x x x0
2
2
2 x0 x x
2
2
2
2
x(2 x0 x)
y 2 x0 x x
2)
2 x0 x
x
x
x
3) lim (2 x0 x) 2 x0
2
x0
х 0
f ( x ) ( x ) 2 х - производная функции
f ( 3 ) 2 ( 3 ) 6 - производная функции в т.
т.е.
2
х0
6.
Схема вычисления производной функции:1. Найти приращение функции на отрезке [ x; x+Δx]:
y y ( x x) y ( x)
2. Разделить приращение функции на приращение
аргумента: y
y ( x x) y ( x)
x
x
3. Найти предел отношения приращения функции к
приращению аргумента, когда приращение аргумента
стремится к нулю.
y
y ( x x) y ( x)
y lim
lim
x 0 x
x 0
x
7.
Задание: Найти производную функции по определению:1.
y x
2.
y C , где С число
3.
4.
5.
3
y kx b, где k и b числа
1
y
x
y x
8.
Решение 1: Вычислить производную функции y1.
x3
f f ( x x) f ( x) ( x x) x
3
3
x 3 3x 2 x 3x x 2 x 3 x 3
3x 2 x 3x x 2 x 3
2.
3.
y 3x 2 x 3x x 2 x 3
3x 2 3x x x 2
x
x
y
2
2
y lim
lim 3x 3x x x
x 0 x
x 0
2
2
lim 3x lim 3x x lim x
x 0
2
x 0
3x 0 0 3x
x 0
2
9.
Решение 2: Вычислить производную функции y C , где С число1.
2.
3.
y y ( x x) y ( x) С С 0
y
0
0
x x
y
y lim
lim 0
x 0 x
x 0
0
10.
Решение 3: Вычислить производную функции y kx b, где k и b числа1.
y y ( x x) y ( x) k x x b kx b
kx k x b kx b k x
2.
3.
y k x
x
x
k
y
y lim
lim k
x 0 x
x 0
k
11.
1y
Решение 4: Вычислить производную функции
x
1
1
y y ( x x) y ( x)
x x x
1 x
1 ( x x) x x x x
x( x x) x( x x)
x( x x) x( x x)
1.
2.
3.
x
y
1
x
x( x x)
2
x
x x x
x( x x) x
x
y
1
1
1
y lim
lim ( 2
) 2
2
x 0 x
x 0 x x x
x 0 x
12.
y xРешение 5: Вычислить производную функции
1.
y y ( x x) y ( x)
2.
y
x
x x x
x
x x x
x x x x x x
x x x x
x x x
x
1
x x x x x x x x x x x
3.
y
1
y lim
lim (
)
x 0 x
x 0
x x x
1
1
x 0 x 2 x
13. Таблица простейших производных
ФУНКЦИЯПРОИЗВОДНАЯ
(С )
0
( х )
1
( х )
n
1
х
( х )
nх
n 1
1
2
х
1
2 х
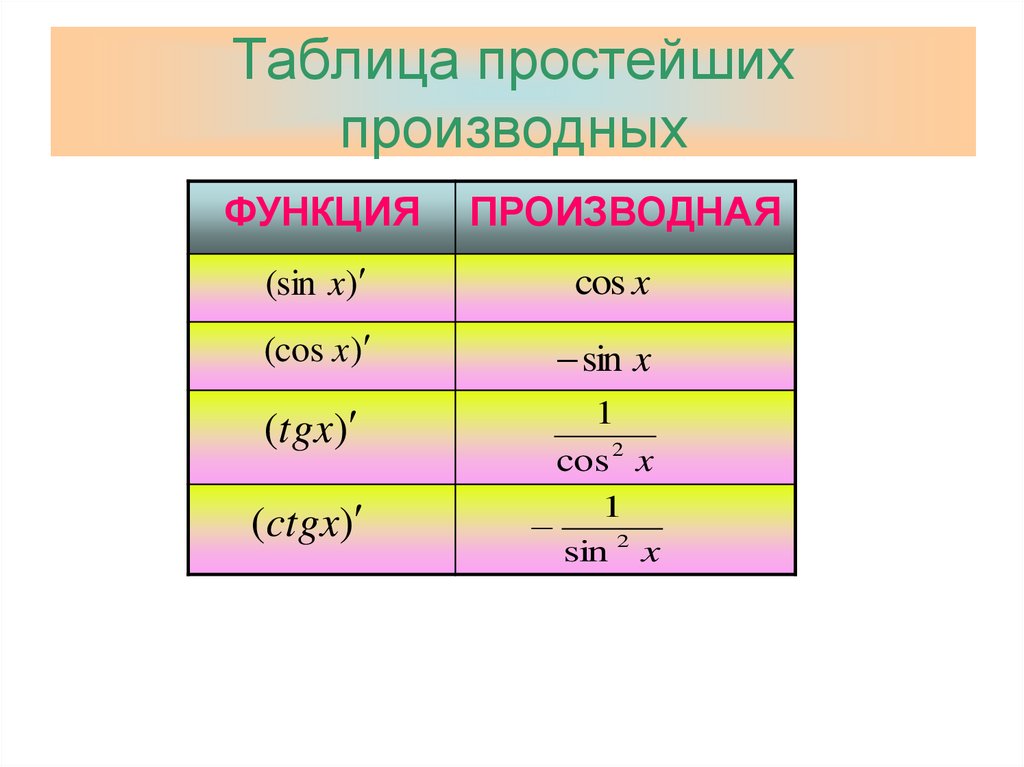
14. Таблица простейших производных
ФУНКЦИЯПРОИЗВОДНАЯ
(sin x)
cos x
(cos x )
sin x
(tgx)
1
cos 2 x
(ctgx)
1
sin 2 x
15. Правила дифференцирования (вычисления производных)
• (1) (u v) u v• (2) (uv) u v uv
u
u
v
u
v
• (3)
2
v
v
С
Сv
1) (Сv) Сv 2) 2
v
v
• Следствия:
16. Фронтальная работа №1
хf ( x)
9
1 2
3
f ( x) (2 x х 4 х 12)
2
4
х
2
f ( x) 10
8 х
3
1)
2)
3)
4)
f ( x) (14 х )
17. Фронтальная работа №1 (продолжение)
6)7/1)
7/2)
3 х2
f ( x)
4
f ( x) ( х (5 2 х))
2
2
2
3
f ( x) ( х (5 2 х)) (5х 2 х )
18.
Фронтальная работа №219. Фронтальная работа №3
x 2xx cos x
;
; 2) f ( x )
1) f ( x)
2x 1
sin x
2
1 x
1 x
;
; 4) f ( x )
3) f ( x)
3
1 x
1 x
2
x 1
5) f ( x) 2 n
x 1
3n


















 mathematics
mathematics








