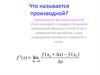Правила вычисления производной

1. . Правила вычисления производной

ГБПОУ АГПК 2020

2. Разминка №4*. Найдите, к чему стремится f(x) (устно)

x31,2,g
g( x(9)x2 ) 0 ,25 при xx
31
32. .f f( (xx) )
x , x 1
2
f
(
x
)
1 4.fff((x(x)x) ) 4g2xg( x
( )x) , x 1, x 4 ?
x 3
4

3. Определение производной

Производной функции y = f(x) в данной
точке x0 называется число, к которому
стремится отношение приращения
функции в этой точке к приращению
аргумента, при условии, что приращение
аргумента стремится к нулю.
Обозначение производной:
f (x )

4. Алгоритм нахождения производной

1.
2.
3.
4.
Найти значение функции в точке x0+∆x: f(x0+∆x)
Найти приращение функции: ∆f = f(x0+∆x) - f(x0)
Найти отношение приращения функции к
приращению аргумента: f
f ( x0 x) f ( x0 )
x
x
Найти выражение ( число) которому стремится
отношение приращения функции к приращению
аргумента при стремлении приращения
аргумента к нулю:
f ( x0 x) f ( x0 )
при х 0
f ( х)
x

5. Задача 1

Докажите, что
1
1
2
х
х
Доказательство:
1
1 x ( x x)
x
f ( x х) f ( x)
x x x
( x x) x
( x x) х
f ( x x)
x
1
x
x
( x x) х
( x x) х
f ( x x)
1
1
1
при х 0
2
x
( x x) х
( х 0) х
х
1
1
1
следовательно f (x) 2 2
х
х
х

6. Задача 2

х 21х
Докажите, что
Доказательство:
f ( x) x , где
f ( x х) f ( x)
х 0 и
f ( x x)
x
x x х
Умножим числитель и знаменатель на
f ( x x)
x
х х 0, тогда
x x х
.
x
x x х , получим :
x x х x x х х х х
1
.
x x x х
x x x х
x x х
при х 0
следовательно
f ( x x)
x
f (x)
1
2 х
1
x x х
х 21х
1
1
х 0 х 2 х

7. Повторение: Некоторые свойства степени с рациональным показателем

1
a 0 1,
3
a 1
a
5
b
7
0
p
1
,
a
где a 0
где a 0
2
4 a
р
a1 a
1
р , где a 0
a
p
b
, где a 0, b 0
a
m
n
60
a n am ,
1
где a 0
a a 2,
где a 0, n N , m Z

8.

Повторение:
Представьте в виде степени с рациональным
показателем
7 7
1.
2.
9
1
2
а а
4
4
9
1
3
3 2 2
3.
2
1
4. b
b b b b
5.
х у x y x y
2
3
1, 5
3
2
1,5

9. Повторение:

№5*. Представьте в виде степени с рациональным
показателем:.
1)
3
2
2
1
2)
1000000
3)
7
х у
2
1
4)
5 у
1
5)
1, 3
х
1
6)
х
7) 5 а
8)
9)
1
у 20
1
х х
х
10) 4
х
11) а 8 а 3

10. Формулы дифференцирования.

1. С = 0
2. ( хп) = n хn-1
3. х = 1
6. (kх + b) = k
1
1
4. х х 2
8. (cosx)'=-sinx
5. х
1
2
х
7. (sinx)'=cosx
1
9. (ctgx)'= sin 2 x
1
10. (tgx)'=
соs 2 x

11. Правила дифференцирования

u v u v
Cu C (u )
Постоянный множитель можно выносить за знак
производной.
uv u v uv Производная произведения
u v uv Производная частного
u
V v
v2

12. Проверьте себя Найдите производную функции

Функция
Производная функции
(правильный ответ)
у = 5х
5
у = - 4х + 1
-4
у = 0,8х - 2
0,8
у = 9х +10
9
у = 12 - 0,7х
-0,7