Производная. Правила вычисления производных

1. Производная

ПРОИЗВОДНАЯ

2.

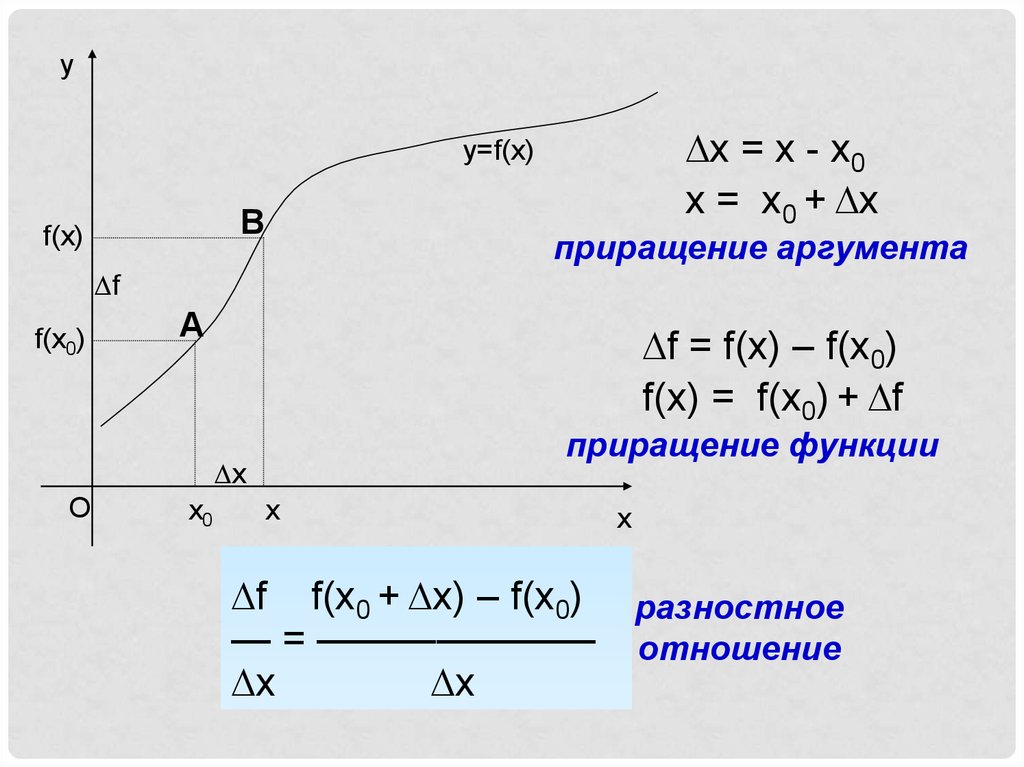
y
x = x - x0
x = x0 + x
y=f(x)
В
f(x)
приращение аргумента
f
f(x0)
А
f = f(x) – f(x0)
f(x) = f(x0) + f
приращение функции
x
O
x0
x
x
f f(x0 + x) – f(x0) разностное
— = ——————— отношение
x
x

3.

y
l
y=f(x)
В
f(x)
f
f
А
f(x0)
O
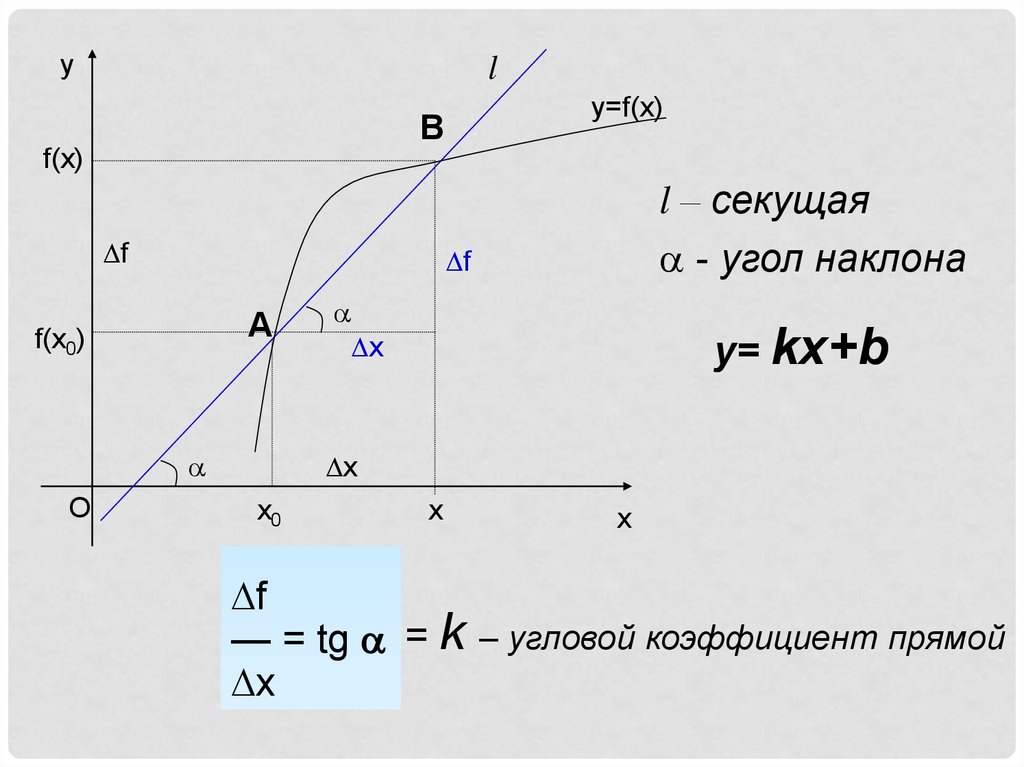
l – секущая
- угол наклона
x
y= kx+b
x
x0
x
x
f
— = tg = k – угловой коэффициент прямой
x

4.

x
Если тело движется по прямой и за время
t его координата изменяется на x, то
t t(x0 + x) – t(x0)
Vср( t) = — = ———————
x
x
- средняя скорость движения тела за t

5.

y
l
l
Вy=f(x)y=f(x)
f(x)
f
А
f(x0)
f
— tg
x
O
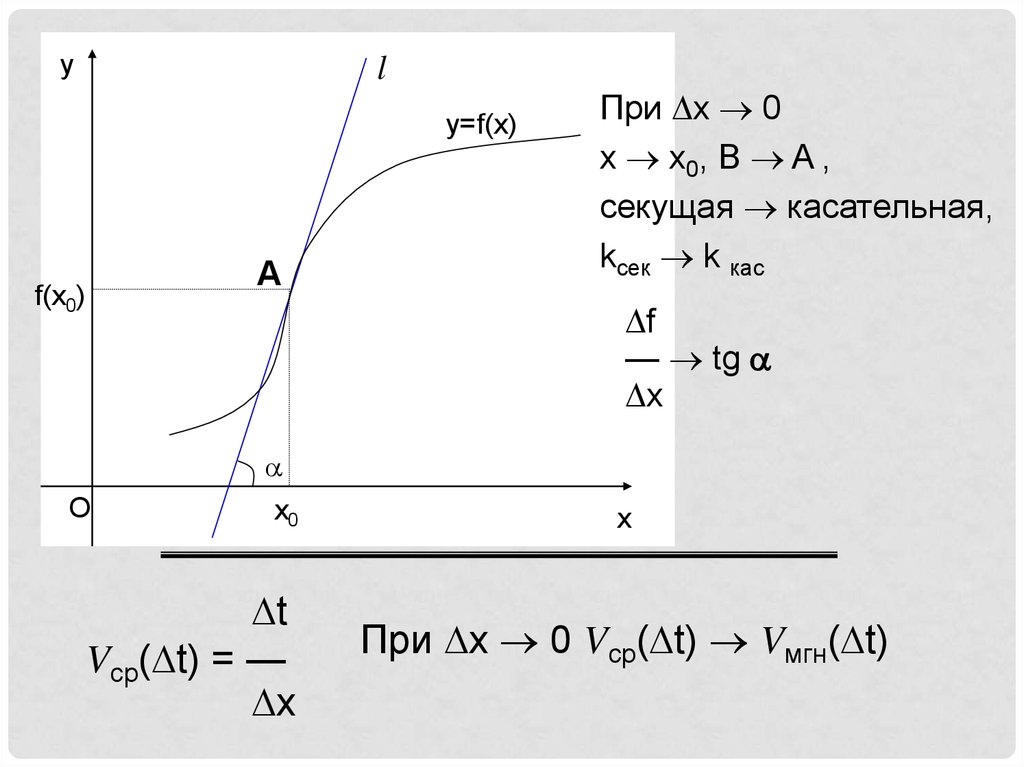
При x 0
x x0, B A ,
секущая касательная,
kсек k кас
x0x0
t
Vср( t) = —
x
x
x
x
При x 0 Vср( t) Vмгн( t)

6.

Производная
Производной функции f в точке x0 называется
число, к которому стремится разностное
отношение при x 0.
f f(x0 + x) – f(x0)
f´(x0)= — = ———————
x
x
при x 0.

7.

Правила вычисления
производных
Если функции U и V дифференцируемы в точке x0, то
1. ( U + V )´ = U´ + V´
2. (U V)´ = U´ V + U V´
3. U ´
U´ V - U V´
— = ——————
V
V2
Если функция U дифференцируема в точке x0, а Спостоянная, то
(СU)´=CU´

8.

Формулы для вычисления
производных
1.
2.
3.
4.
5.
C´ = 0
x´ = 1
(xn)´= nxn-1
1
( x)´= ——
2 x
1 ´
1
— = - ——
x
x2

9.

Задание 1. Найдите производные функций:
1. f(x)=3x+5
2. f(x)=4x2-5x3+9x
3
x
3. f(x)= — + —
x
3
2
5
7
4. f(x) = — + — - —
x2 x3 x
5. f(x)= x + 4
1
1
6. f(x) = — + — + 4x
3x 2x2

10.

Задание 2. Найдите производные функций:
1. f(x)=(3x+5)(x-3)
2. f(x)=(x2-5x)(x3-x2)
3+x
3. f(x)= ——
x3
2x2 - 5
4. f(x) = ———
x+1
5. f(x)= ( x + 4) ( x - 2)
1
1
6. f(x) = — + — 4x2
2
x