Similar presentations:
Решение уравнений, содержащих переменную под знаком модуля
1.
Решение уравнений,содержащих переменную
под знаком модуля
Родионова Г. М., учитель математики МБУ «Школа №82»
г.о.Тольятти
2.
Определение модуляa, a 0,
а
a, a 0.
0
a
a
|a|
| a |
х
3.
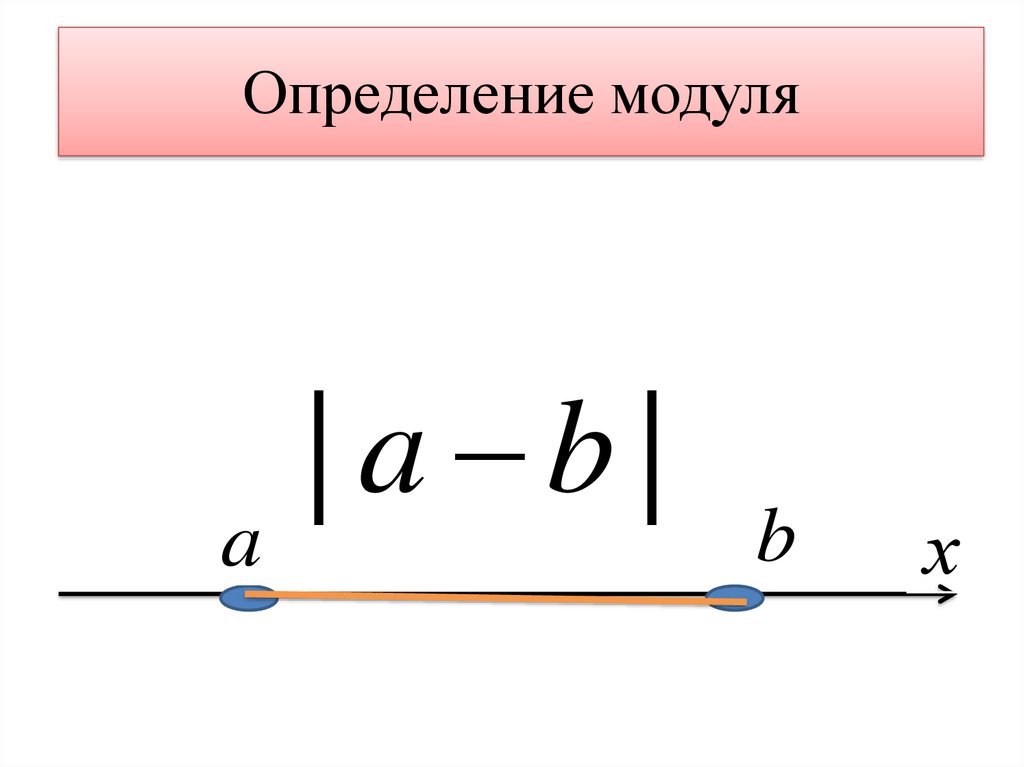
Определение модуляa
| a b|
b
х
4.
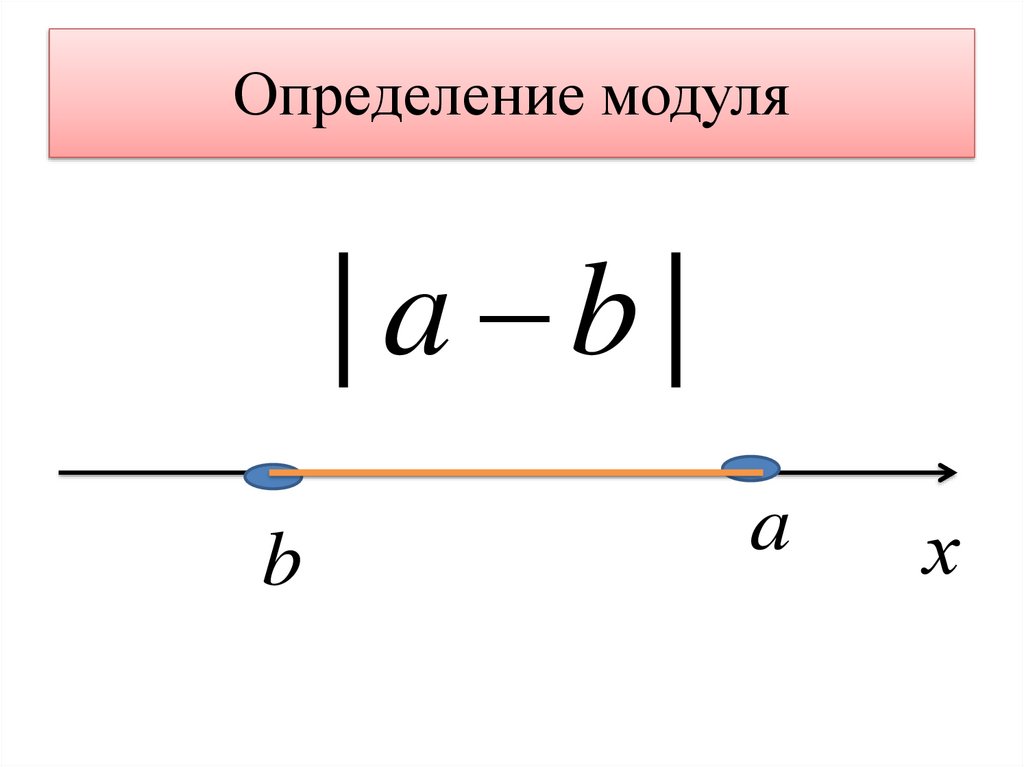
Определение модуля| a b|
b
a
х
5.
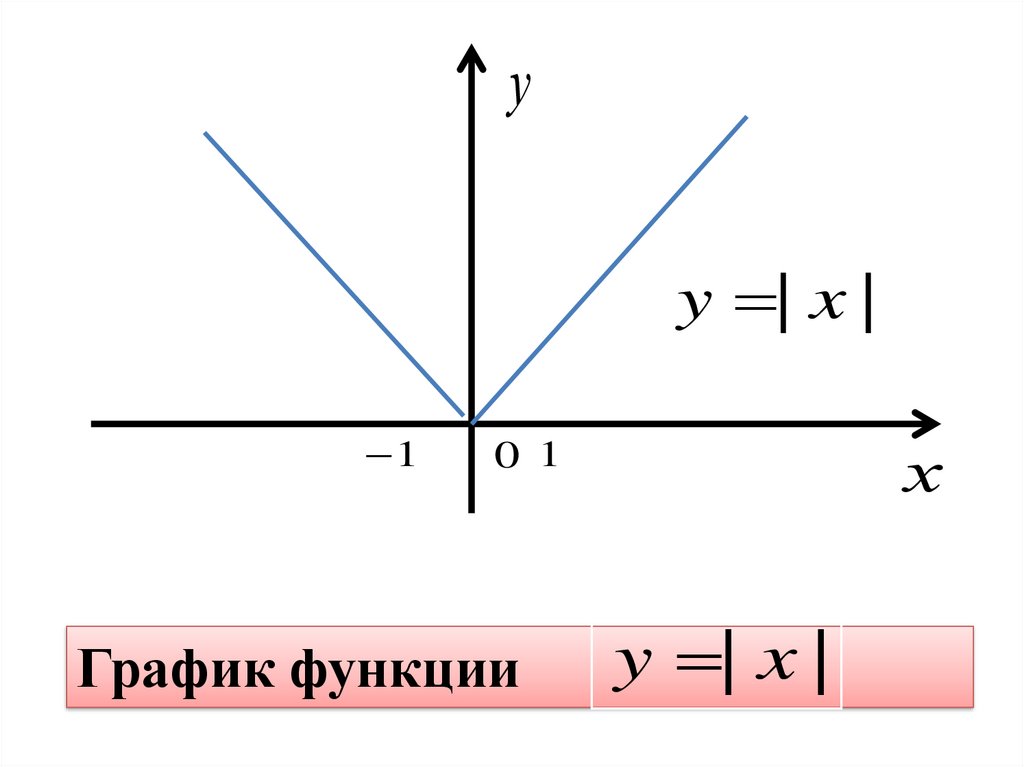
уy | x |
1
х
0 1
График функции
y | x |
6.
Решение уравнений с модулемf ( x ) a,
1. | f ( x) | a, а 0
f ( x) a.
при а 0 решений нет
7.
Решите уравнения:1. 2 х 3 5
2. 2 х 5 х 3
2
8.
Решение уравнений с модулемf ( x) g ( x),
2. | f ( x) | | g ( x) |
f ( x) g ( x).
9.
Решите уравнения:1. 2 х 3 6 х
2. 2 х 2 5 х х 2 4
10.
Решение уравнений с модулемf ( x) 0,
f ( x) g ( x),
3. | f ( x) | g ( x)
f ( x) 0,
f ( x) g ( x).
g ( x ) 0,
4. | f ( x) | g ( x ) f ( x) g ( x),
f ( x) g ( x).
11.
Решите уравнения:1. 2 х 3 5 х
2. 2 х 5 х 3 х
2
12.
Решите уравнение:х2 4 х 3 0
х 4 х 3 0
2
х2 4 х 3 0
2 2
2
х t х х t х 0
2
х 4 х 3 0
2
t
1,
х 4х 3 0
2
t 4t 3 0
t х3 0
Обратная замена
х 1,
х 1,
х 3
х 3
13.
Задание на дом14.
6 способов решенияодного уравнения
| x 1 | | x 3 | 4
15.
Уравнение с модулемРешить уравнение
| x 1 | | x 3 | 4
I способ.
Решение:
Найдем нули
подмодульных
выражений
x 1 0, x 1
x 3 0, x 3.
Для раскрытия двух модулей рассмотрим
следующие 4 случая:
16.
x 1 0a) x 3 0
или
x 1 x 3 4;
x 1 0
б ) x 3 0
x 1 x 3 4;
x 1 0
в) x 3 0
или
или
x 1 x 3 4;
x 1 0
г ) x 3 0
x 1 x 3 4;
17.
x 1a ) x 3
x 1;
x 1
б ) x 3
0 x 8;
Решений нет
Решений нет
x 1
в ) x 3
0 x 0;
x 1
г) x 3
x 3;
x 3.
1 x 3.
Ответ: [-1;3]
18.
Решите уравнение| x 1 | | x 3 | 4
II способ.
Так как обе части уравнения неотрицательные,
то при возведении их в квадрат получим
уравнение равносильное данному.
(| x 1 | | x 3 |) 2 4 2 ,
( x 1) 2 2 | x 1 | | x 3 | ( x 3)) 2 16,
| x 2 2 x 3 | x 2 2 x 3.
Из определения модуля следует. Что последнее
равенство выполнимо, если x 2 2 x 3 0,
т.е. когда
x [ 1;3].
Ответ: [-1;3]
19.
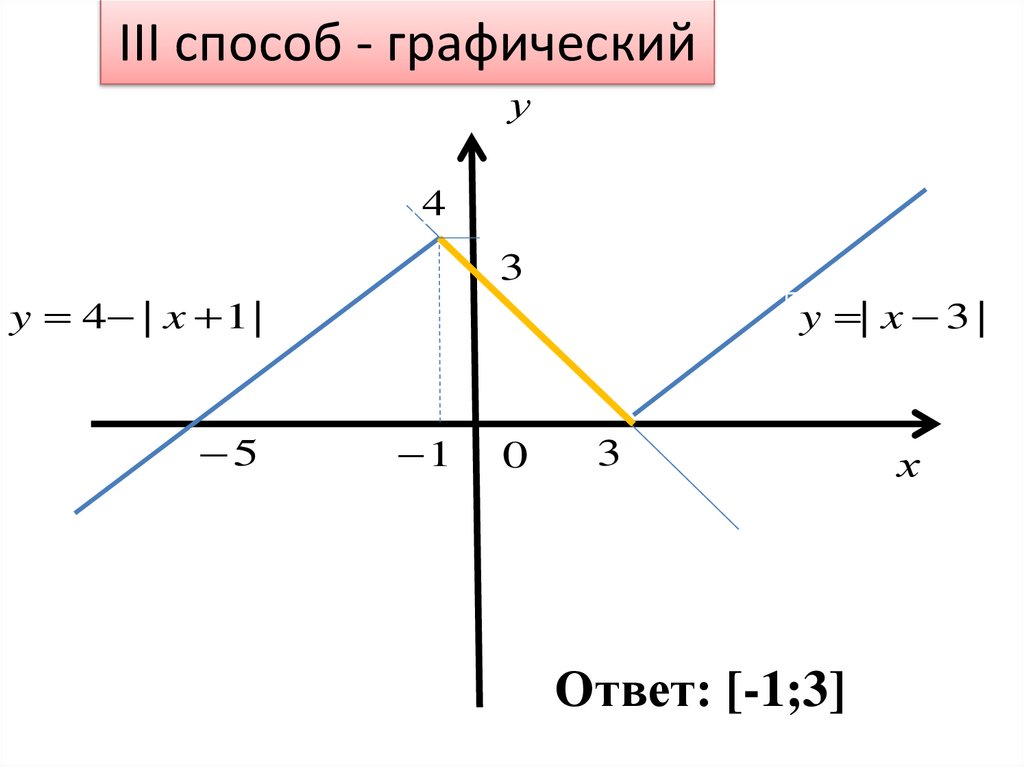
III способ - графическийПерепишем данное уравнение в
следующем виде:
| x 3 | 4 | x 1 | .
Далее изобразим графики функций
y | x 3 |, y 4 | x 1 |
И укажем абсциссы их общих точек.
Графики совпадают при x [ 1;3].
Ответ: x [ 1;3].
20.
III способ - графическийу
4
3
y 4 | x 1 |
5
y | x 3 |
1
0
3
Ответ: [-1;3]
х
21.
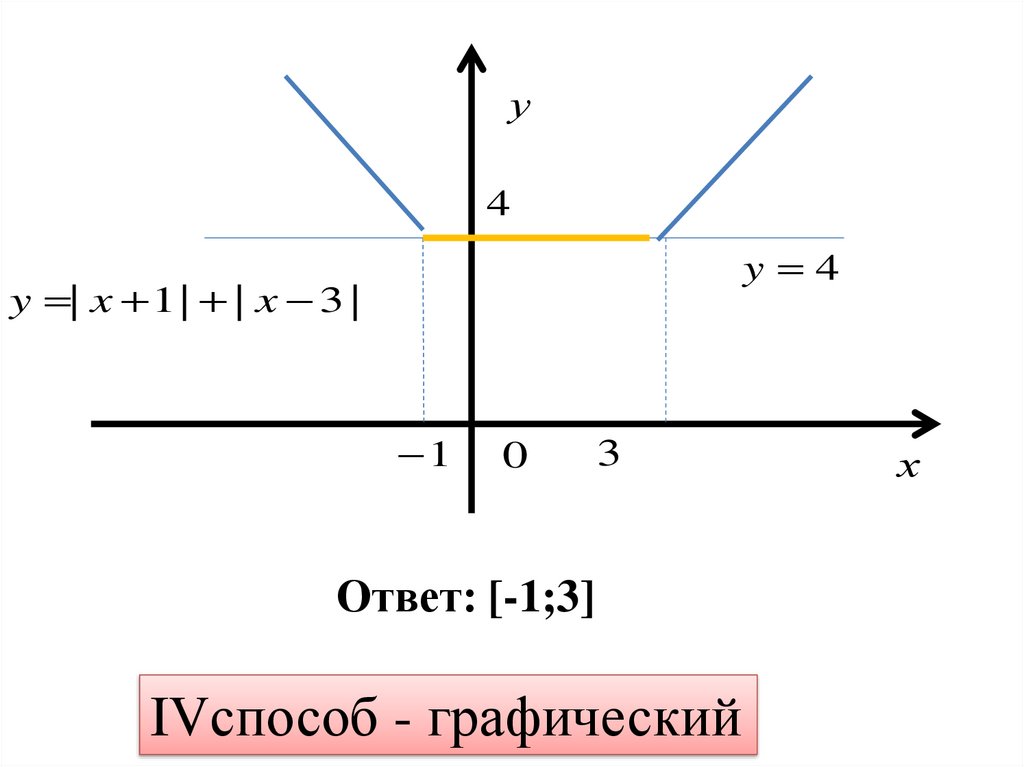
IVспособ - графическийНайдем абсциссы общих точек графика
функции y | x 1 | | x 3 |
и прямой y 4.
Для построения первого графика
достаточно взять несколько точки
с абсциссами х < 1 и x > 3, после
чего последовательно соединить их до
получения ломаной.
22.
у4
y 4
y | x 1 | | x 3 |
1
0
3
Ответ: [-1;3]
IVспособ - графический
х
23.
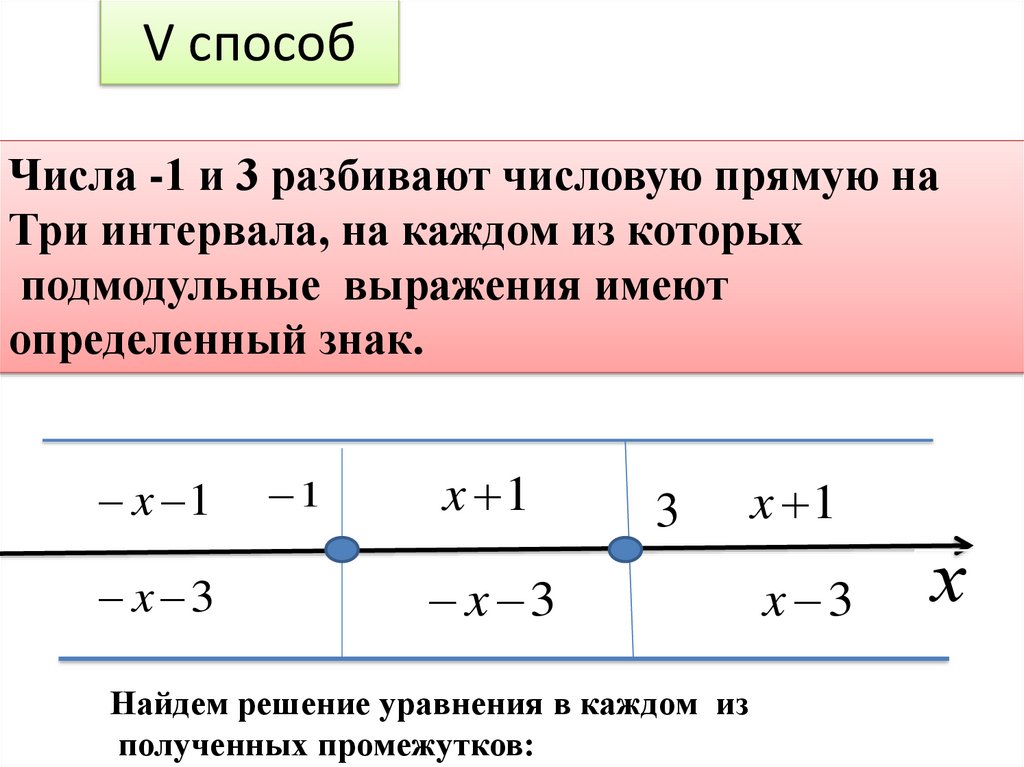
V способЧисла -1 и 3 разбивают числовую прямую на
Три интервала, на каждом из которых
подмодульные выражения имеют
определенный знак.
x 1
x 3
1
x 1
3
x 3
Найдем решение уравнения в каждом из
полученных промежутков:
x 1
x 3
х
24.
x ( ; 1)a)
x 1 x 3 4;
x [ 1;3]
б )
x 1 x 3 4;
x (3; )
в)
x 1 x 3 4;
или
или
25.
x ( ; 1)a)
x 1;
Нет решения
x [ 1;3]
б )
0 x 0;
x [ 1;3]
x (3; )
в )
x 3;
Ответ: [-1;3]
26.
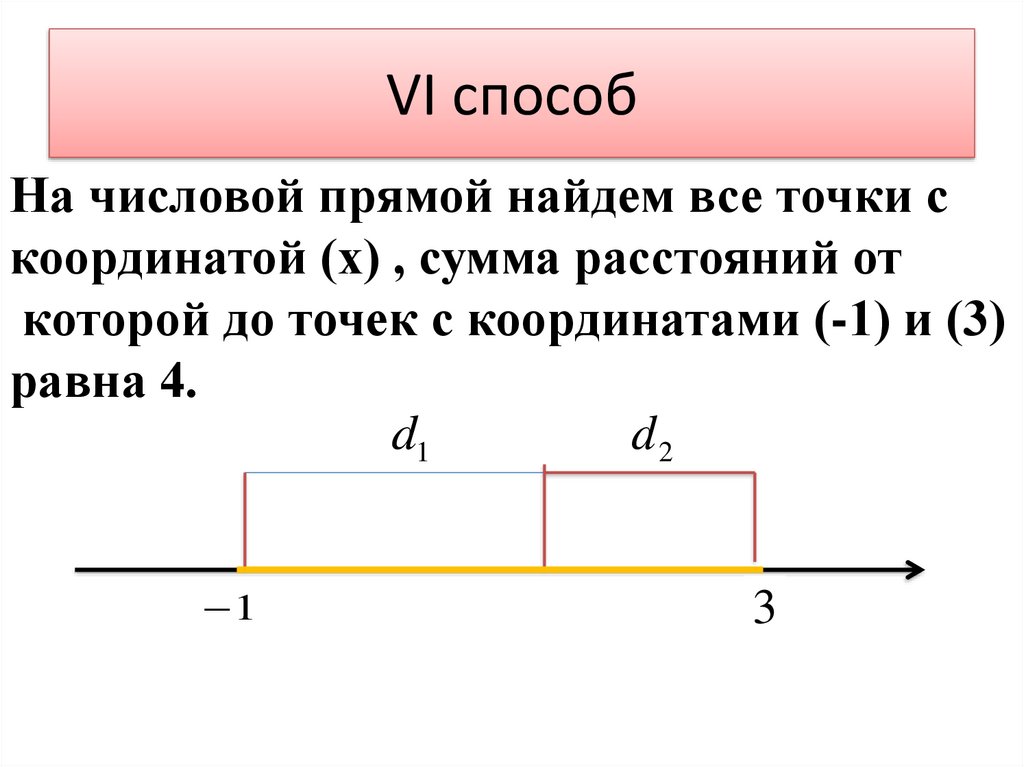
VI способНа числовой прямой найдем все точки с
координатой (х) , сумма расстояний от
которой до точек с координатами (-1) и (3)
равна 4.
d1
d2
1
3
27.
Литература:•Алгебра 9кл: учеб. для общеобразоват. учреждений
Мордкович А.Г .– М.: Мнемозина, 2017.
•Журнал «Математика в школе» №3,2010 , стр.31.
•Алгебра: Нестандартные задачи: экспрессрепетитор для подготовки к ГИА: 9-й кл./Г.В.
Сычева, Н.В. Гусева,В.А. Гусев,-М.:АСТ:Астрель
; Владимир: ВКТ, 2010












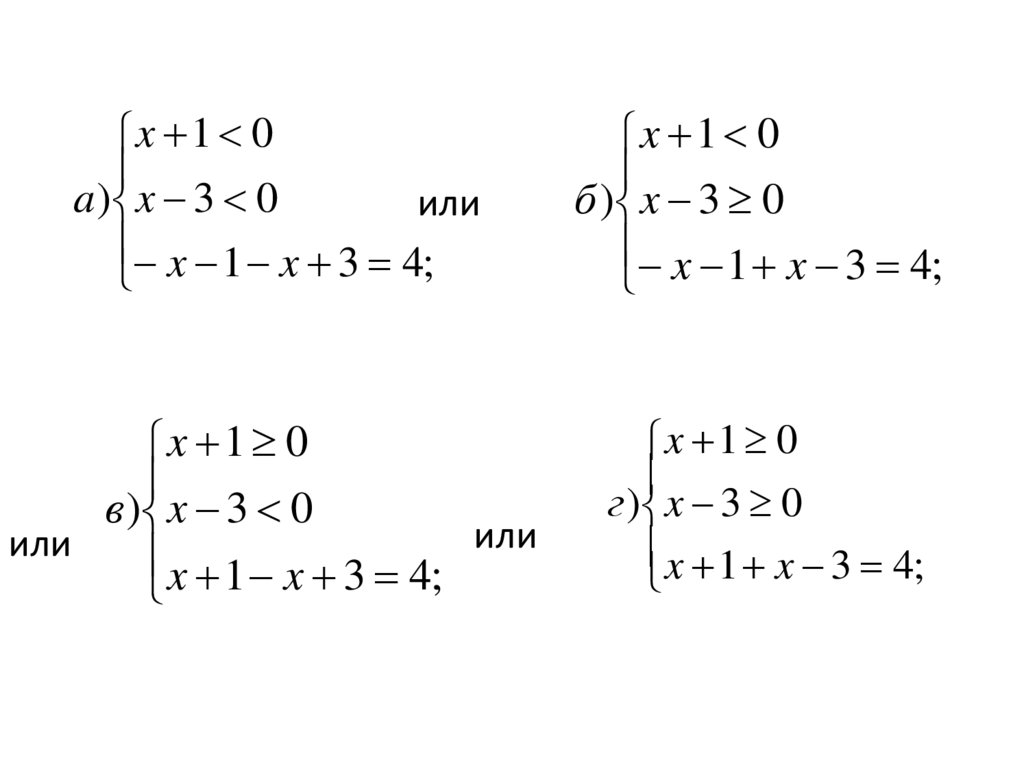




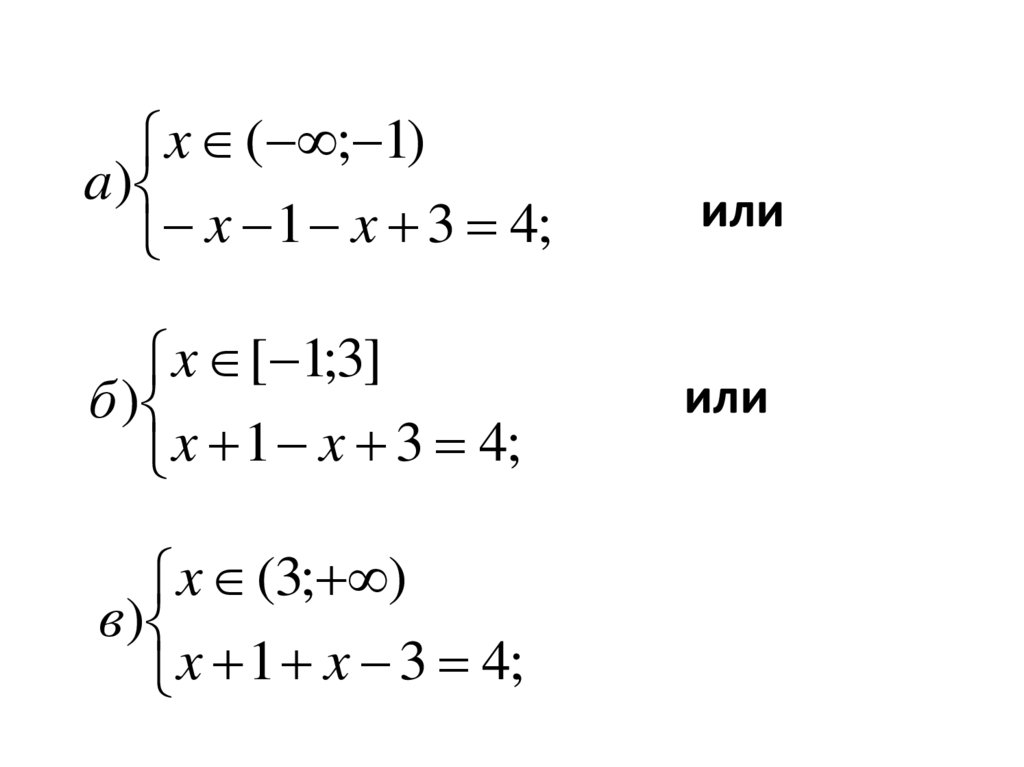


 mathematics
mathematics








