Уравнения и неравенства с переменной под знаком модуля

1.

ТЕМА
Разработала:
Богданова Ольга Николаевна
учитель математики
МКОУ «Овечкинская средняя
общеобразовательная школа
Завьяловского района»
Алтайского края

2.

Обобщить и систематизировать
знания о модуле, полученные
ранее
Формировать умения решать
уравнения и неравенства,
содержащие переменную под
знаком модуля
Формировать умения строить
графики функций, содержащих
знак модуля
Воспитывать привычку
систематически трудиться и
преодолевать трудности

3.

Определение модуля
Геометрический смысл модуля
Свойства модуля
Основные способы решений уравнений с переменной
под знаком модуля
Основные способы решений неравенств с
переменной под знаком модуля
Способы построения графиков функций,
содержащих переменную под знаком
модуля
Проверь себя
Литература
Глоссарий
Физминутка
Выход

4.

Модуль – это абсолютная
величина
а
a, если a 0
a, если a 0

5.

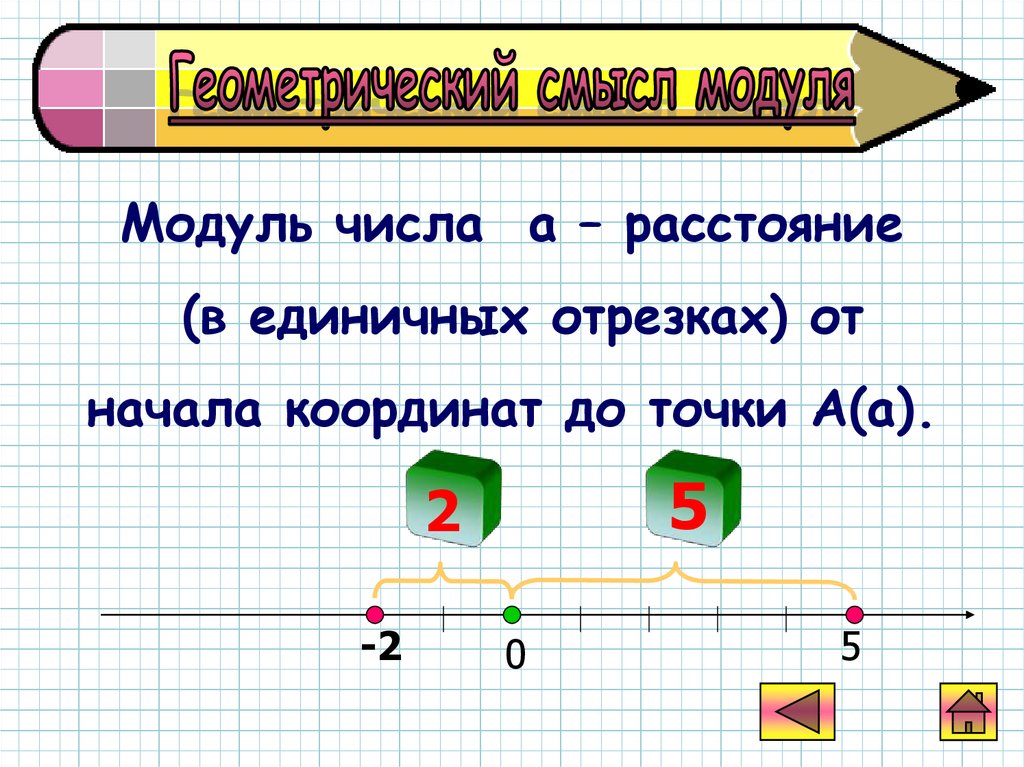
Модуль числа a – расстояние
(в единичных отрезках) от
начала координат до точки А(a).
5
2
-2
0
5

6.

а 0, а
а а, а
a
a
,b 0
b b
m
а а , а
а a , m Z
аb a b
a b a b , a, b
2
a a
m
a b a b , a, b

7.

Уравнения вида|х|=b
Уравнения вида |f(x)|=a
Уравнения вида |f(x)|=g(x)
Уравнения вида |f(x)|=|g(x)|
Прием последовательного раскрытия
модуля
Метод интервалов

8.

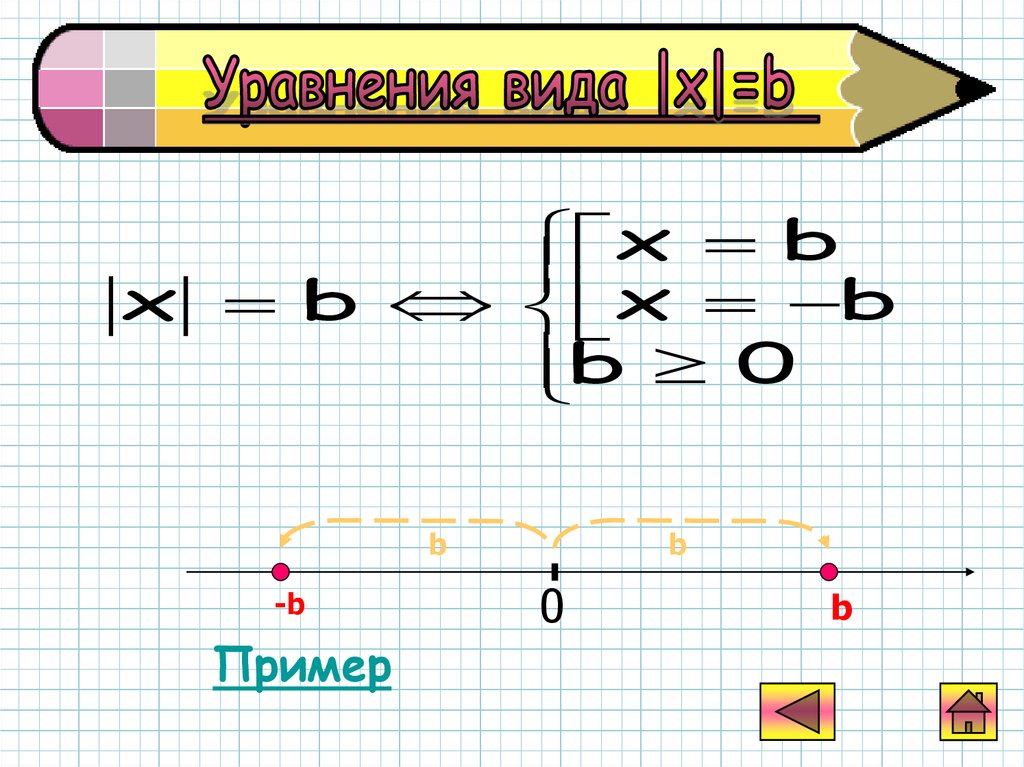
x b
x b
x b
b 0
b
-b
Пример
b
0
b

9.

f x а
f x a
f x а
f x a
a 0
Пример

10.

f x g x
f x
f x
f x g x
f
x
f x
Пример
0
g x
0
g x

11.

f x g x
f x g x
f x g x f x g x
g x 0
Пример

12.

f x g x
g x 0
f x g x 2
2
f
x
g
x
Пример

13.

f x g x
f x g x
f x g x
f x g x
Пример

14.

f x g x
f x g x f x g x
2
Пример
2

15.

Метод заключается в
последовательном раскрытии
модуля в задачах , где
внутри одного модуля
находится другой, или
несколько.
Пример

16.

С помощью метода интервалов
(или метода разбиения на
промежутки) решаются
уравнения вида
f1 x f2 x fn x g x

17.

Для этого находим сначала все точки, в которых
f1 x 0, f2 x 0,..., fn x 0
Эти точки делят область допустимых
значений уравнения на промежутки, на
каждом из которых все функции сохраняют
знак (определяем знак каждого модуля на
указанном промежутке). Затем переходим от
уравнения к совокупности систем, не
содержащих знаков модуля.
Пример

18.

Неравенства вида |x|< b и |x|> b
Неравенства вида |f(x)|< a и |f(x)|> a
Неравенства вида |f(x)|< g(x) и |f(x)|> g(x)
Неравенства вида |f(x)|< |g(x)| и |f(x)|> |g(x)|
Прием последовательного раскрытия модуля
Метод интервалов

19.

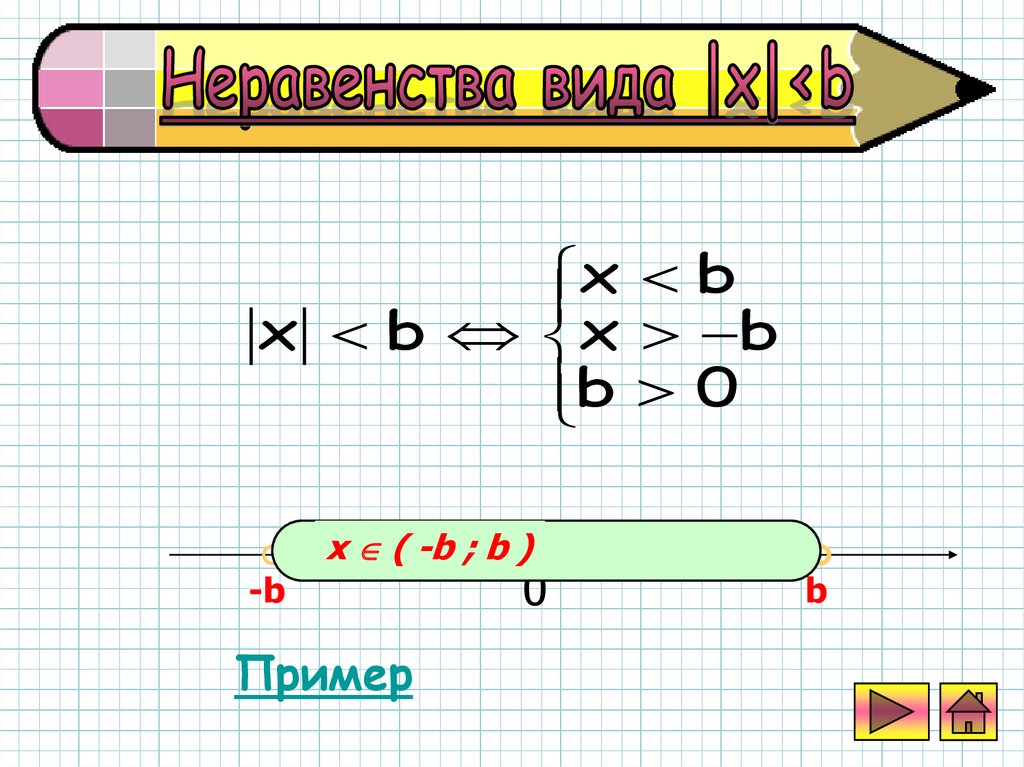
x
b
x b x b
b 0
x ( -b ; b )
-b
Пример
0
b

20.

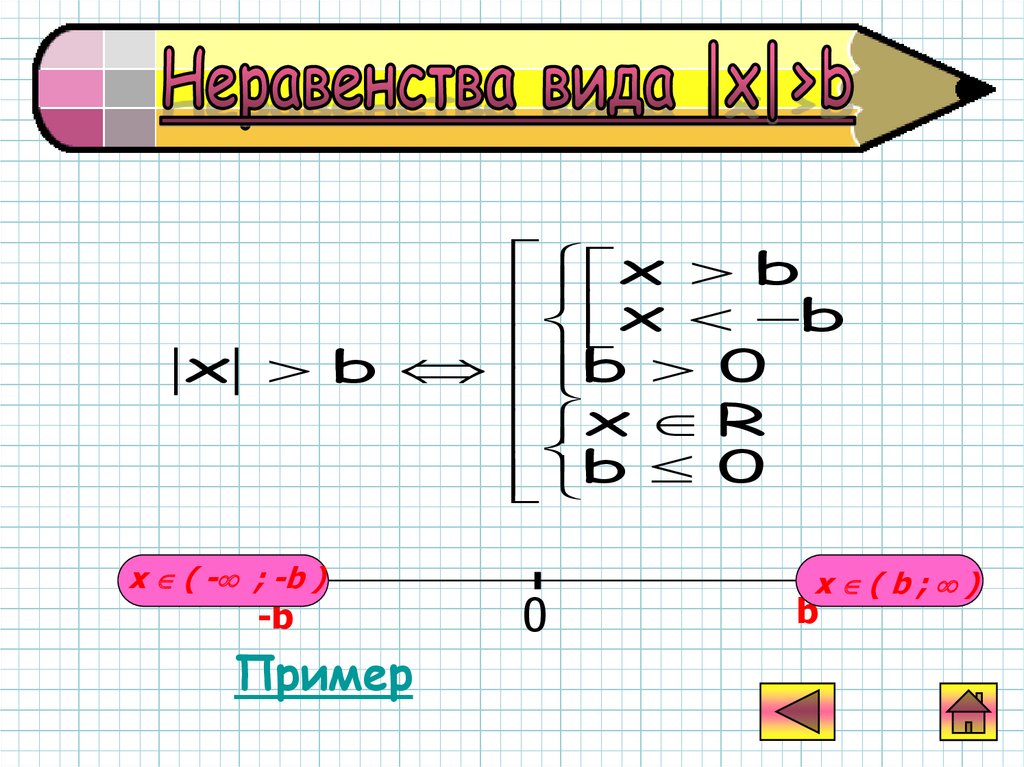
x b
x b
b 0
x b
x R
b 0
x ( - ; -b )
-b
Пример
0
x (b; )
b

21.

f x a
f x a
f x a f x a
a
0
Пример

22.

f x a
f x a
f x a
f x a
a 0
x R
a 0
Пример

23.

f x g x
f x g x
f x g x
f x g x
Пример

24.

f x g x
f x g x
f x g x
f x g x
Пример

25.

f x g x
f x g x f x g x
2
Пример
2

26.

f x g x
f x g x f x g x
2
Пример
2

27.

Метод заключается в
последовательном
раскрытии модуля в
задачах, где внутри одного
модуля находится другой,
или несколько.
Пример

28.

С помощью метода
интервалов (или метода
разбиения на промежутки)
решаются неравенства вида
f1 x f2 x fn x g x

29.

Для этого находим сначала все точки, в которых
f1 x 0, f2 x 0,..., fn x 0
Эти точки делят область допустимых
значений неравенства на промежутки, на
каждом из которых все функции сохраняют
знак (определяем знак каждого модуля на
указанном промежутке). Затем переходим от
неравенства к совокупности систем, не
содержащих знаков модуля.
Пример

30.

Функция у =|х|
Функция у=|х|+а
Функция у=а|х|
Функция у=|x+a|
Функция y= -|x|
Функция y=f(|x|)
От теории к практике

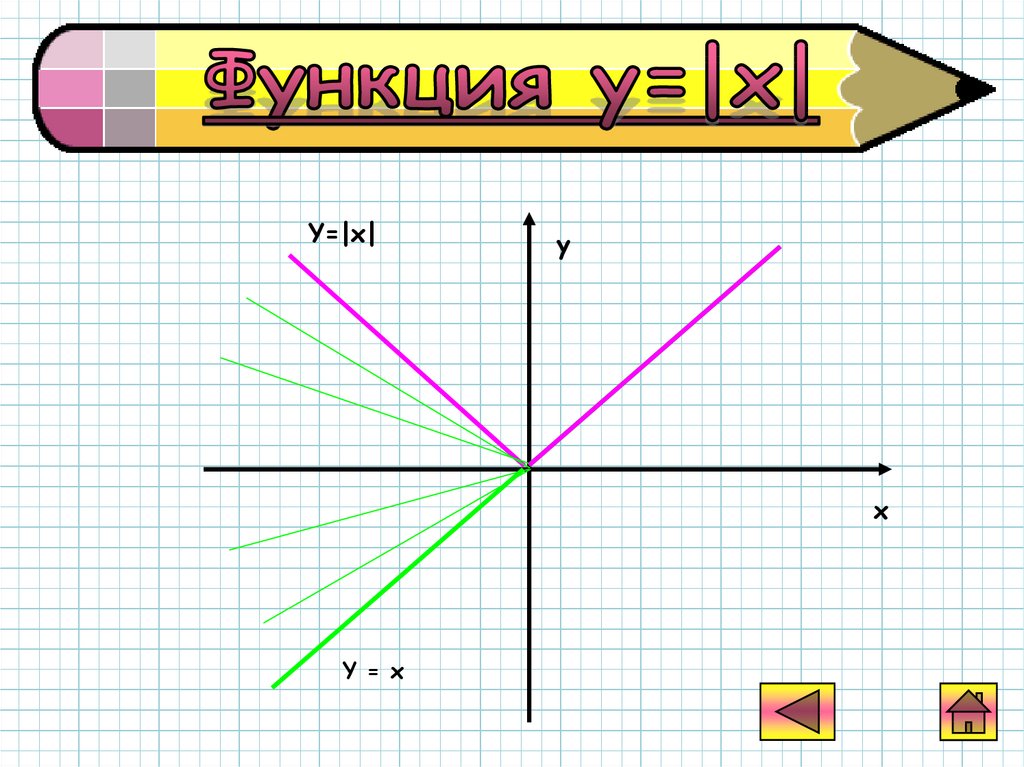
31.

Для построения
графика функции y=|x|
достаточно построить
график функции y=x и
отобразить
симметрично
относительно оси Ох ту
часть графика, которая
расположена ниже оси,
оставив верхнюю часть
графика без изменения.

32.

Y=|x|
у
х
Y = х

33.

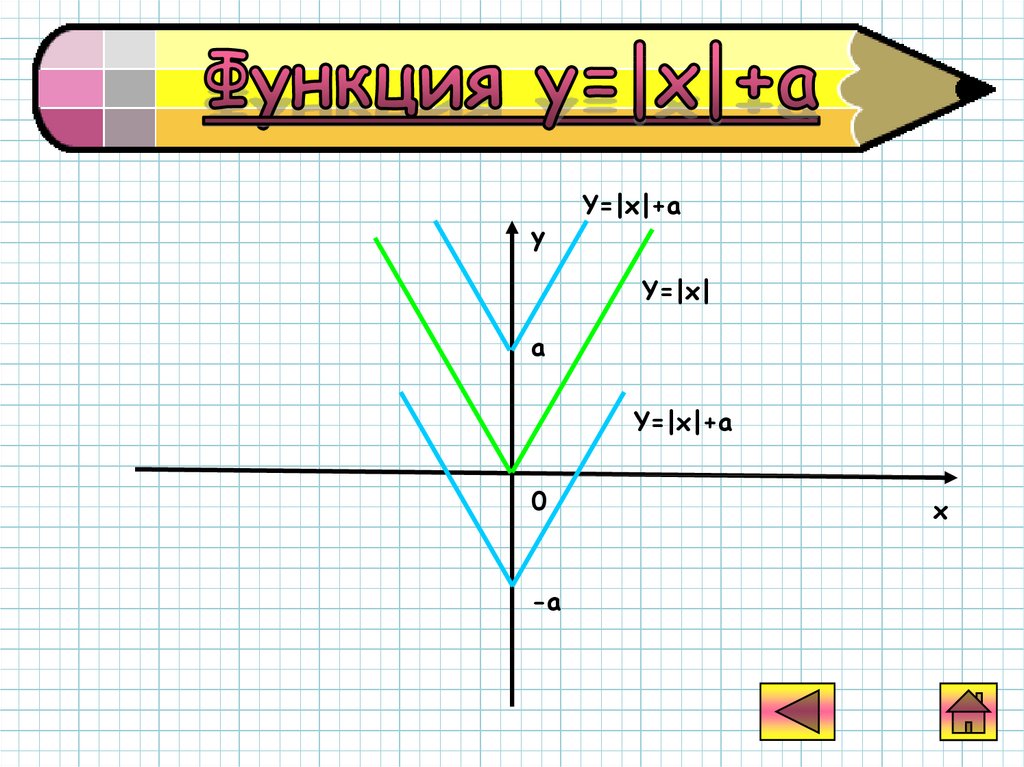
График функции у=|х|+а
получается из графика
функции у=|х| с
помощью
параллельного переноса
вдоль оси Оу на |а|
единиц вверх ,, если
а>0, и вниз на |а|, если
а<0.

34.

y
Y=|x|+а
Y=|x|
a
Y=|x|+а
0
-a
x

35.

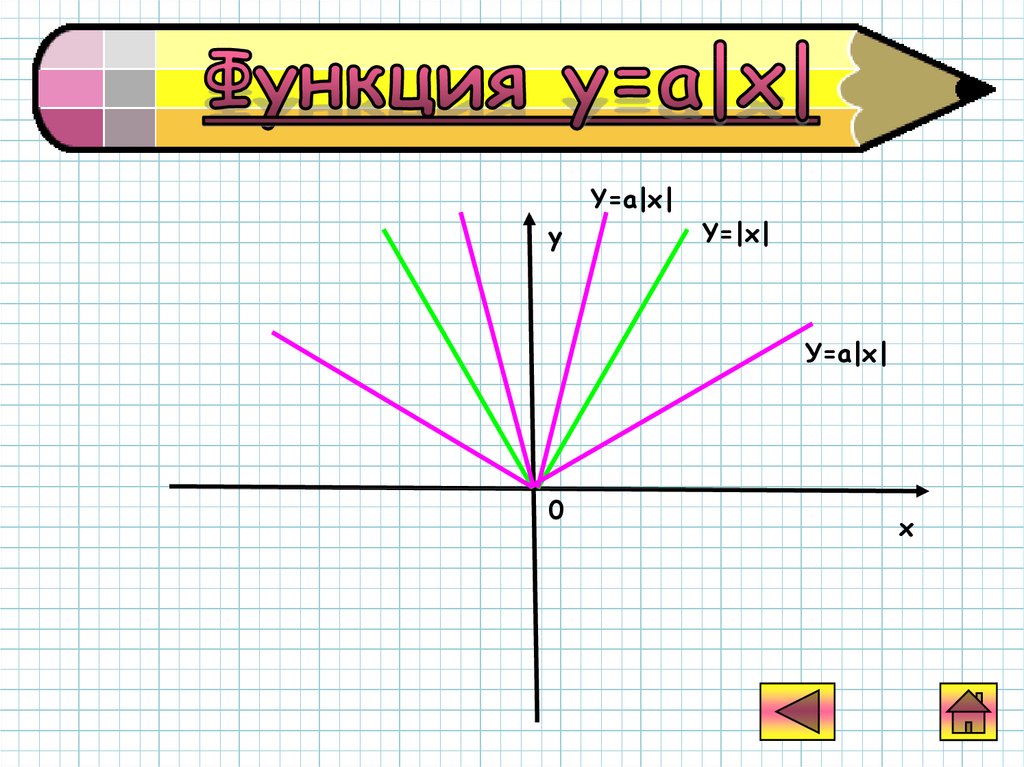
График функции
у=а|х| получается
растяжением
графика у=|х| вдоль
оси Оу в а раз при
а>1 и сжатием
вдоль этой оси в
1/а раз при 0<a<1.

36.

Y=a|x|
y
Y=|x|
У=a|x|
0
x

37.

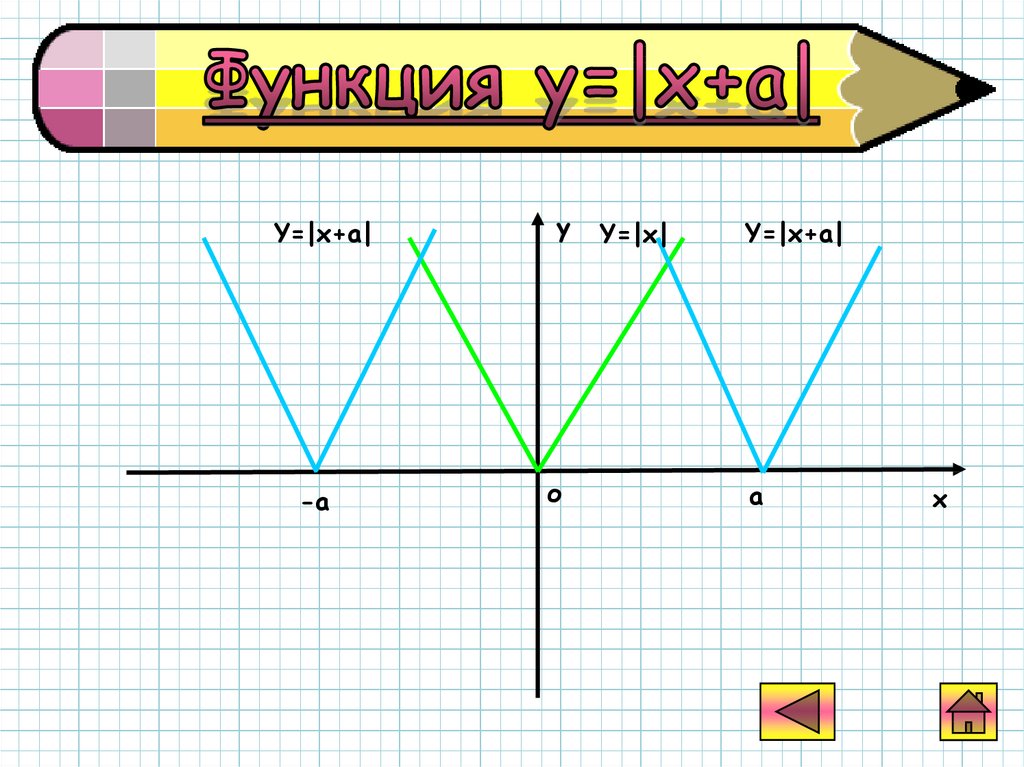
График функции у=|x+a|
получается из графика
функции y=|x| с
помощью параллельного
переноса в
отрицательном
направлении от оси Ох
на |а| единиц, если
а>0,и в положительном
направлении на |a|,
если a<0.

38.

-a
у
о
Y=|x+a|
Y=|x|
Y=|x+a|
a
х

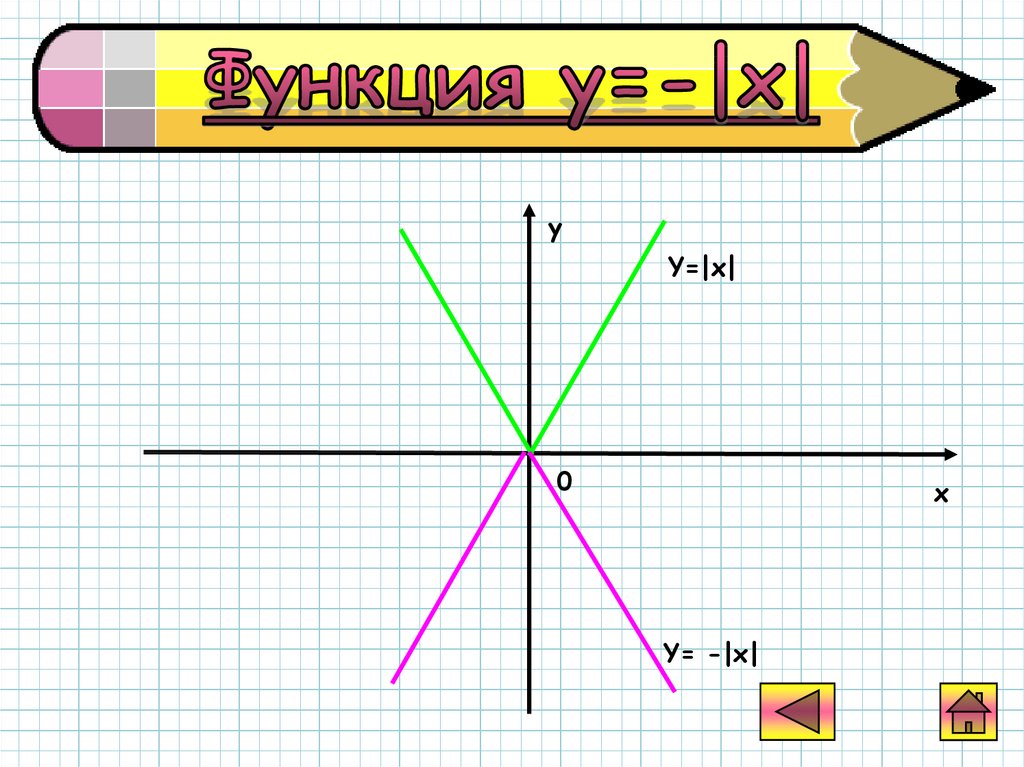
39.

График функции
y= -|x|
получается из
графика функции
y=|x| с помощью
симметрии
относительно оси
Ох .

40.

y
Y=|x|
0
x
Y= -|x|

41.

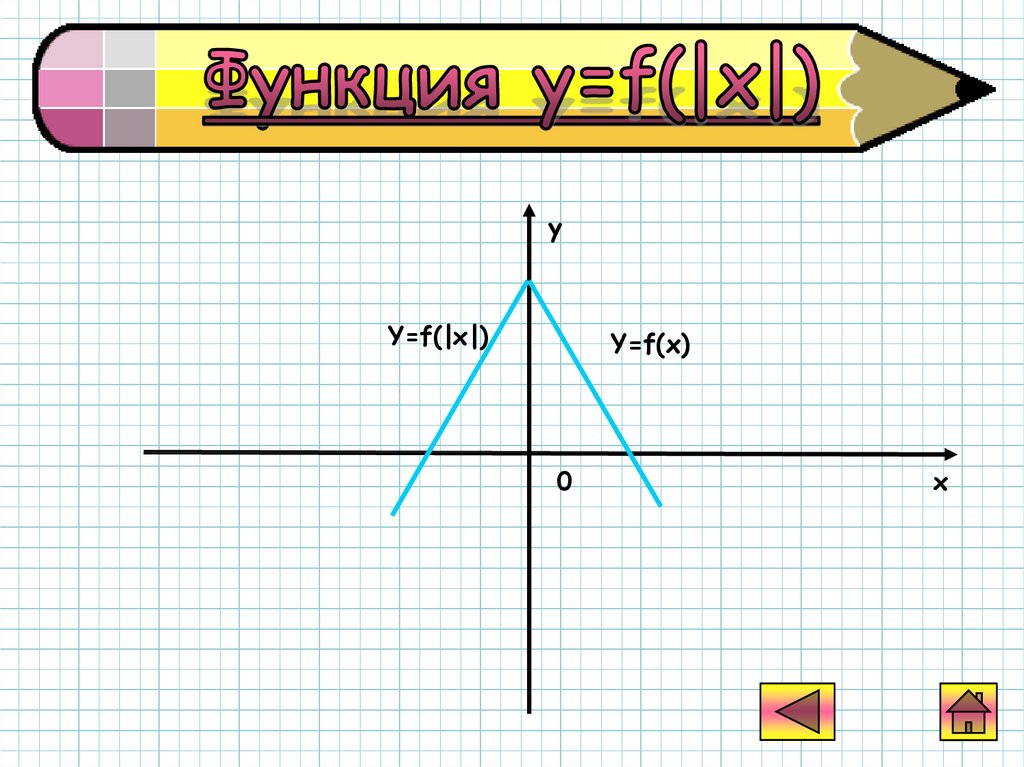
Для построения графика
функции y=f(|x|)
достаточно построить
график функции y=f(x)
при при х>0 или х =0,
а затем отобразить
построенную часть
симметрично оси Оy.

42.

y
Y=f(|x|)
Y=f(x)
0
x

43.

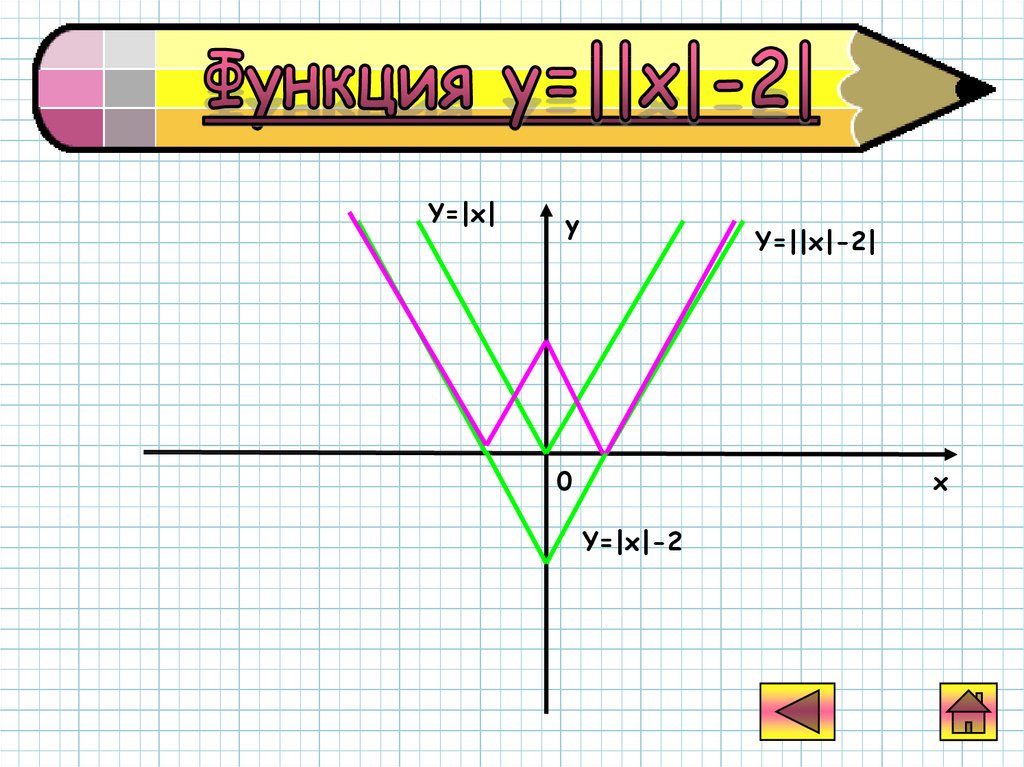
Рассмотрим построение более сложных
графиков.
Задание. Построить график функции
у=||x|-2|.
Построение.
1) Строим график функции y=|x|.
2) Смещаем его вдоль оси Оу вниз на 2
единицы.
3) Отображаем часть графика,
расположенного ниже оси Ох,
симметрично этой оси, в верхнюю
полуплоскость.

44.

Y=|x|
y
Y=||x|-2|
0
x
Y=|x|-2

45.

Коржуев А.В. Построение графиков некоторых
функций //Математика в школе.-1995, №3.
Кочарова К.С. Об уравнениях с модулем
//Математика в школе.-1995, №2.
Севрюков П.Ф. Уравнения и неравенства с модулями.М., 2004 г.
Севрюков П.Ф., Смоляков А.Н .
Уравнения и неравенства с модулями
и методика их решения .-М., 2005.

46.

Параллельный перенос – преобразование, при котором
точки смещаются в одном и том же направлении
на одно и то же расстояние.
Две точки А и В называются симметричными
относительно прямой с, если эта прямая проходит
через середину отрезка АВ и перпендикулярна к
нему.
График функции – множество всех точек координатной
плоскости, абсциссы которых равны значениям
аргумента, а ординаты – соответствующим
значениям функции.

47.

Выход

48.

Решите уравнение:
х 6
1) х 6 х 6
Ответ: 6, 6
2) х 17 решений
нет, так как 17 0
Ответ:

49.

Решите уравнение:
2х 3 5
2х 3 5
2х 3 5
х 4
х 1
Ответ: 4, 1

50.

Решите уравнение:
x2 7 x 6 x 1
x2 7 x 6 x 1 x2 8x 5 0
x 4 11
x 1, x 6
x 1, x 6
x2 7 x 6 0
x2 7 x 6 x 1 2
2
x 6x 7 0 x 3 2
x 7 x 6 x 1
1 x 6
1 x 6
x2 7 x 6 0
Ответ: 4 11, 3 2

51.

Решите уравнение:
x2 7 x 6 x 1
x 2 7 x 6 x 1
2
2
x 7 x 6 x 1 x 7 x 6 x 1
x 1 0
x2 8x 5 0 x 4 11
2
x 6x 7 0 x 3 2
x 1 0
x 1
Ответ: 4 11, 3 2

52.

Решите уравнение:
х 3 2х 3
2x 3 0
х 1,5
x 3 2x 3
2
2
2
2
x 3 2x 3 х 3 2х 3 0
х 1,5
х 1,5
х 3 2х 3 0 х 6
х 3 2х 3 0 х 0
Ответ: х 0

53.

Решите уравнение:
х 7 х 9
х 7 х 9
х 7 х 9
х 7 9 х
0х 2 решений нет
х 8
2х 16
Ответ: 8

54.

Решите уравнение:
х 7 х 9
х 7 х 9 х 7 х 9
х 7 х 9 0
2
2
х 7 х 9 0 х 7 х 9 0
0х 2 решений нет
2х 16
х 8
Ответ: 8
2
2

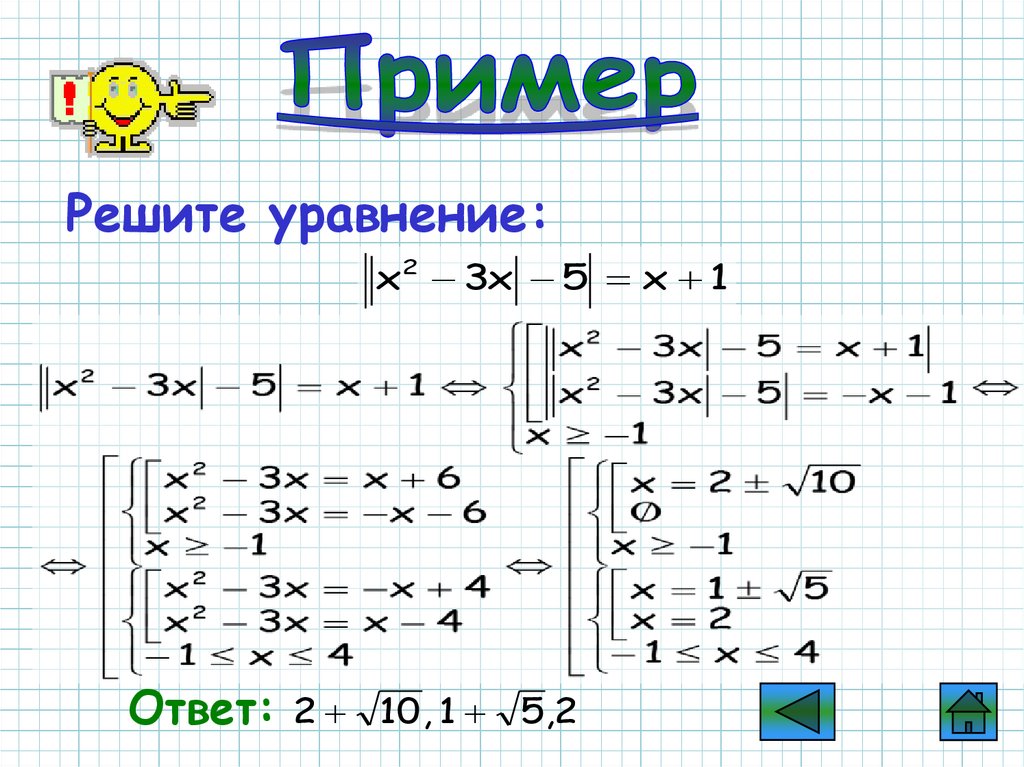
55.

Решите уравнение:
x2 3x 5 x 1
Ответ:
2 10 , 1
5,2

56.

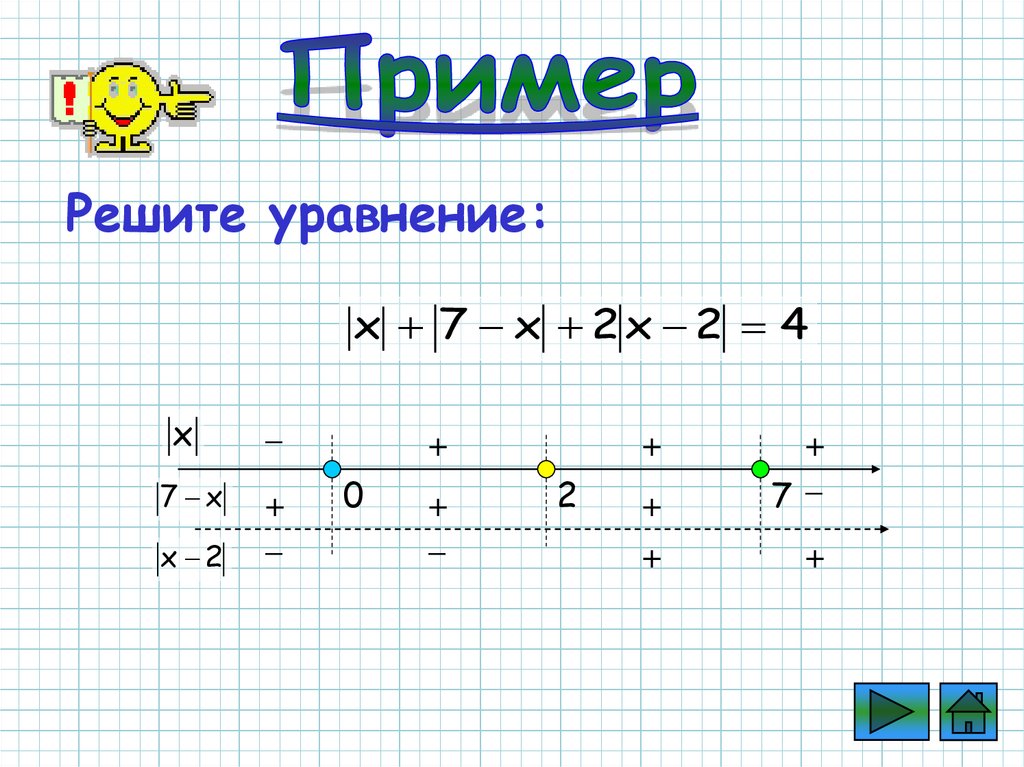
Решите уравнение:
x 7 x 2x 2 4
x
7 x
x 2
_
+
_
+
0
+
_
+
2
+
+
7
+
_
+

57.

x 0
x
0
,
1
x 7 x 2 x 2 4 x 7 ;
4
0 x 2,
0
x
2
,
2
x 7 x 2 x 2 4 x 7 ;
2
2 x 7,
2 x 7,
3
x 7 x 2 x 2 4 x 1 ;
2
x 7
x 7
15
4
x
7
x
2
x
2
4
x
;
4
Ответ: корней нет
нет решений
нет решений
нет решений.
нет решений

58.

Решите неравенство:
x 7
x 7
x 7
x 7
Ответ: 7 ;7

59.

Решите неравенство:
х 16
х 16 х R
Ответ: x R

60.

Решите неравенство:
2х 5 1
2x 5 1
2x 5 1
2x 5 1
2x 6
x 3
x 2
2x 4
Ответ:
2;3

61.

Решите неравенство:
7 2х 3
7 2х 3
7 2х 3
7 2x 3
x 2
2x 4
x 5
2x 10
Ответ: ; 5 2;

62.

Решите неравенство:
4x 5 2x 7
4x 5 2x 7
4x 5 2x 7
4x 5 2x 7
x 6
2x 12
1
6x 2
x 3
1
Ответ: ; 6;
3

63.

Решите неравенство:
3x 8 7x 4
3x 8 7 x 4
3x 8 7 x 4
3x 8 4 7 x
x 3
4x 12
x 3
x 0,4
10x 4
Ответ: 3;

64.

Решите неравенство:
x 4 3x 1
x 4 3x 1 x 4 3x 1
2
2
х 4 3х 1 0
х 0,75
2х 5 4х 3 0
х 2,5
2
Ответ: 0,75;2,5
2

65.

Решите неравенство:
x 3 3x 2
x 3 3x 2 x 3 3x 2
2
2
x 6x 9 9x 12x 4
1
x
2
4
8x 18x 5 0
5
x
2
5 1
Ответ: ;
2
2 4
2

66.

Решите неравенство:
x2 3x 2 1 x 2
2
2
x
3
x
2
1
x
2
x
3x 2 x 1
2
x 3x 2 1 x 2 2
2
x 3x 2 1 2 x x 3x 2 3 x
x2 3x 2 x 1
x 1, x 3
x2 3x 2 1 x
нет решений
2
x 3x 2 3 x 1 2 x 1 2
x2 3x 2 x 3 x ;
Ответ: ;1 2 3;

67.

Решите неравенство:
4х 1 1 2х x
4х 1
2х 1
_
_
-1/4
+
_
+
1/2 +

68.

1
1
2 1
x
x
1)
4
4 x 3 ; 4
3x 2
4x 1 2x 1 x
1
1
1
1
1
x
x
2) 4
4
2
2 x 4 ;0
5x 0
4x 1 2x 1 x
1
1
x
x
3)
2
2 решений нет
x 2
4x 1 2x 1 x
2
Ответ: 3 ;0

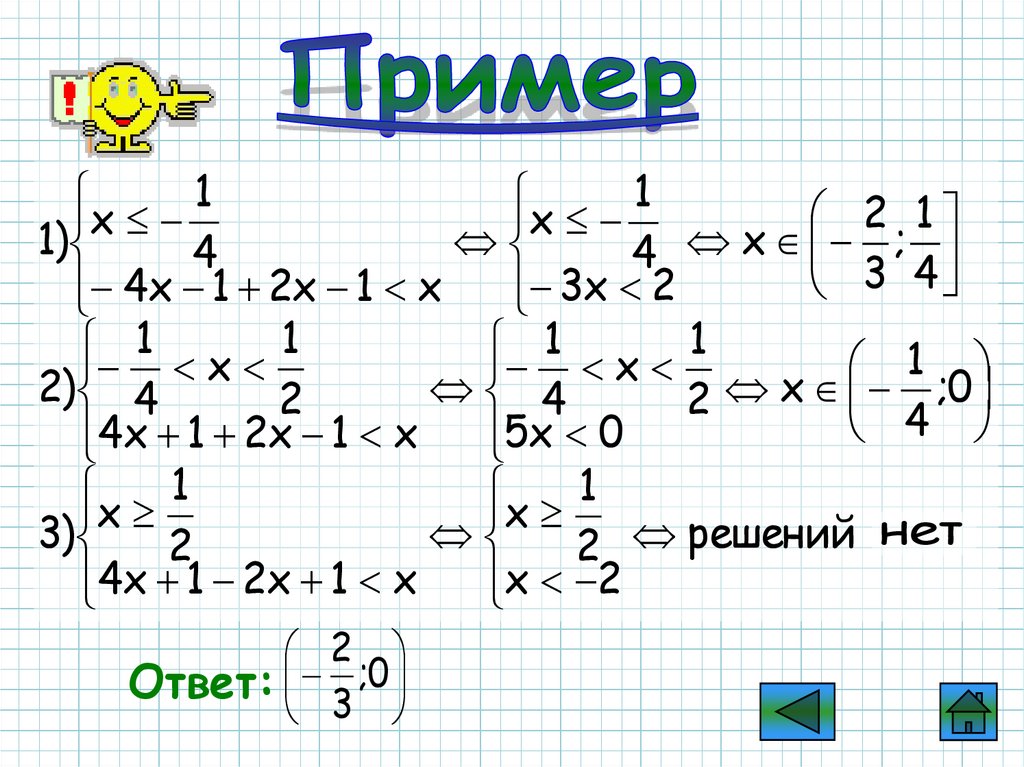
69.

Найдите наименьшее целое решение
неравенства:
x 10,5 2
А. 10
Б. 12
В. 9
Г. 8

70.

Решите уравнение:
x 7 x 12 x 4
2
А.–4
Б. 4
В. 2; 4
Г. 2

71.

Найдите наименьший корень уравнения:
x 1 x 2 3
А.-2
Б. 12
В.–3
Г. 1

72.

Найдите сумму целых решений неравенства:
x 3 3x 2
А. 0
Б. -2
В. -3
Г. 7

73.

Найдите наименьшее целое решение
неравенства:
x 10,5 2
x 10,5 2
x 12,5
x 10,5 2 x 10,5 2 x 8,5
Ответ: 9

74.

Решите уравнение:
x 7 x 12 x 4
2
x2 7 x 12 x 4
2
2
x 7 x 12 x 4 x 7 x 12 x 4
x 4 0
2
x
4
0
x2 8x 16 0
x 2
x 2
x2 6x 8 0
x 4
x 4
x 4
x 4
x 4
Ответ: 4

75.

Найдите наименьший корень уравнения:
x 1 x 2 3
х 1
х 2
_
_
_
-2
+
1
+
+

76.

x 2,
x 2
1 x 1 x 2 3 x 2; нет решений
2 x 3,
2 x 3,
2 x 1 x 2 3 0 x 0; x - 2;3
x 3
x 3
x 3
3 x 1 x 2 3 2x 2; x 1; нет решений
Ответ: 2

77.

Найдите сумму целых решений неравенства:
x 3 3x 2
x - 3 3x 2 x 3 3x 2
2
2
x 6x 9 9x 12x 4
5
x
2
8x2 18x 5 0
1
x
4
2
Ответ: 3
2

78.

Решение

79.

80.

81.

Решение

82.

Решение

83.

84.

85.

86.

87.

88.

89.

90.

91.

92.

93.

Решение

94.

95.

96.

Комплекс упражнений
гимнастики для глаз
1.Быстро поморгать, закрыть глаза и
посидеть спокойно, медленно
считая до пяти.
2.Крепко зажмурить глаза, открыть
их и посмотреть вдаль.
3.Вытянуть правую руку вперед.
Следить глазами за медленными
движениями указательного пальца.