Уравнения, содержащие знак модуля

1.

МАТЕМАТИКА
Уравнения,
содержащие знак
модуля
Лекцию подготовили: Спицына Татьяна, Суворова Ольга
Руководитель: Калугина Екатерина Евгеньевна

2.

ЛЕКЦИЯ№3
Литература
В помощь учащимся лицея –
интерната при СГАУ им. Н. И. Вавилова «
Сборник задач по математике Часть I»
Уравнения,
содержащие знак модуля.

3.

План лекции
Проверка домашнего задания
Алгоритмы решения уравнений, содержащих
переменную под знаком модуля:
f(x) g(x)
f(x) g(x)
f1 (x) f2 (x) ... fn (x) g(x)

4.

Вопрос № 1. Какие выражения называются
уравнениями?
Вопрос №2. Что называется корнем уравнения?
Что значит решить уравнение ?
Вопрос № 3. Из предложенных уравнений выберите:
2x 2 3 0
3x + 4 = 10
а) пару равносильных уравнений;
б) уравнение и уравнение следствие.
2x + 5 = -7
Равносильные
уравнения
Уравнение и уравнение
следствие
x 2 4x + 4 = 0
x 2 - 5x + 6 = 0
2x 2 3 0
2x + 5 = -7
3x + 4 = 10
x 2 - 5x + 6 = 0

5.

Алгоритм решения уравнения
f(x) a, a R
Если a 0
f(x) a
Если a 0
f(x) 0
Уравнение корней не
имеет
f(x) 0
I способ
Если a 0
II способ
f(x) a f(x) 0; f(x) a,
f(x) = a; f(x) a.
f(x) < 0;
f(x) = -a.

6.

Решите уравнение
x x
x 2 2x 3 1
x x
Уравнение
корней не имеет
x 0
Уравнение
корней не имеет
x 0
x (x 2)
x 2 (x 2) 0
x 5 2
2
Уравнение
корней не имеет
2
x = - x -1
x
x
x 2
Уравнение
корней не имеет
1
x 0

7.

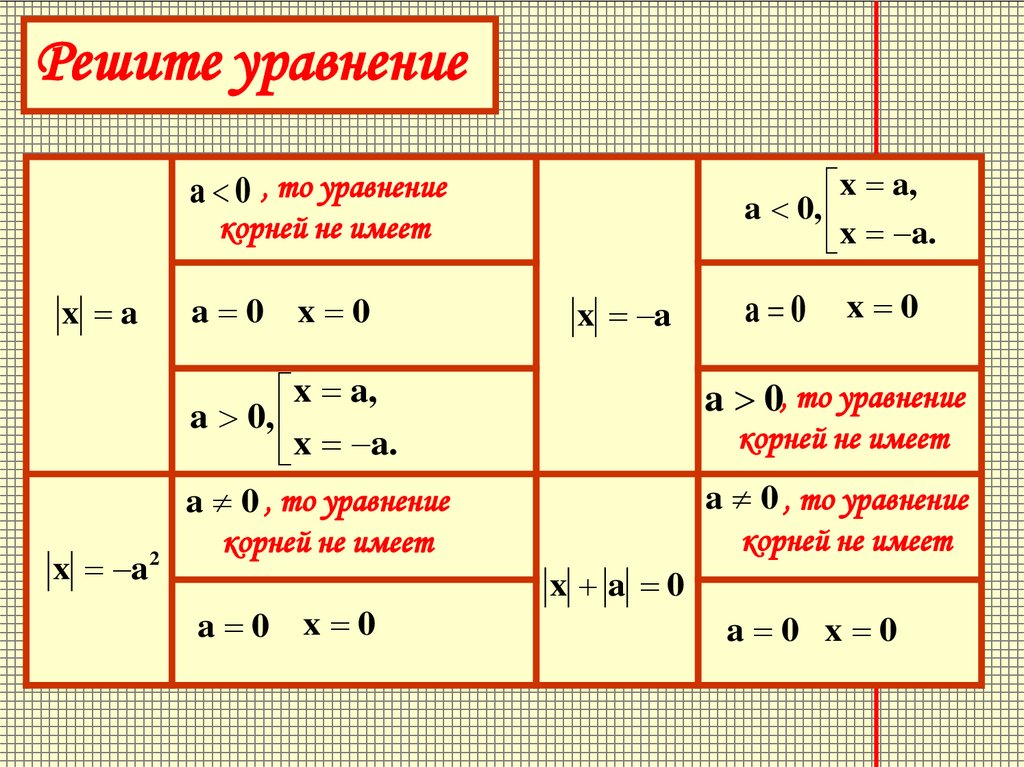
Решите уравнение
x a,
a 0,
x a.
a 0 , то уравнение
корней не имеет
x a
x a2
a 0
x 0
x a
x a,
a 0,
x a.
a 0 , то уравнение
корней не имеет
a 0
x 0
a 0
x 0
a 0, то уравнение
корней не имеет
a 0 , то уравнение
корней не имеет
x a 0
a 0 x 0

8.

Алгоритм решения уравнений
По определению
модуля уравнение
f(x) g(x)
равносильно
совокупности
f (x) g (x),
f(x) g(x)
f(x) 0,
g(x) 0,
f(x) = g(x);
f(x) 0,
g(x) < 0,
f(x) = -g(x);
f(x) < 0,
g(x) 0,
-f(x) = g(x);
f(x) < 0,
g(x) < 0,
f(x) = g(x).
2
2
f 2 (x) g 2 (x) 0,
f(x) g(x)
Уравнение
f(x) g(x)
равносильно
совокупности
f(x) g(x),
f(x) g(x) f(x) g(x) 0,
f(x) g(x).
f(x) g(x) 0,
f(x) g(x) 0;
f(x) g(x),
f(x) g(x).

9.

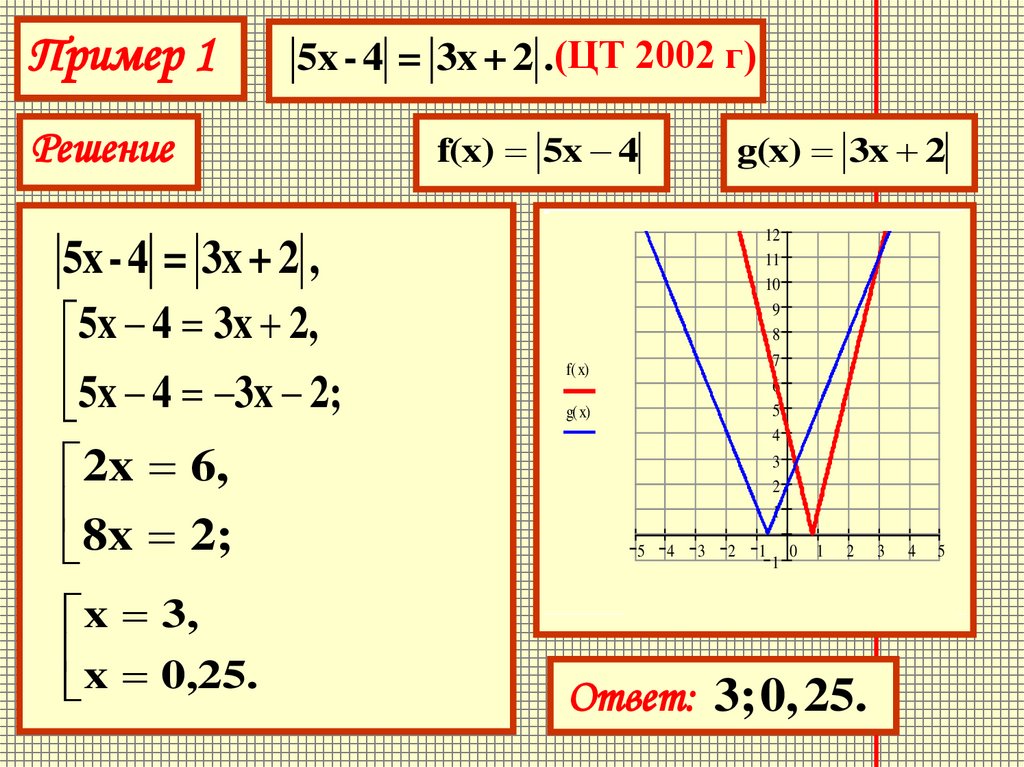
Пример 1
5x - 4 = 3x + 2 .(ЦТ 2002 г)
Решение
5x - 4 = 3x + 2 ,
5x 4 3x 2,
5x 4 3x 2;
2x 6,
8x 2;
x 3,
x 0,25.
f(x) 5x 4
g(x) 3x 2
12
11
10
9
8
12
7
6
5
4
f( x)
g( x)
3
2
1
1
5
5
4
3
2
1
1
0
1
2
x
Ответ: 3;0, 25.
3
4
5
5

10.

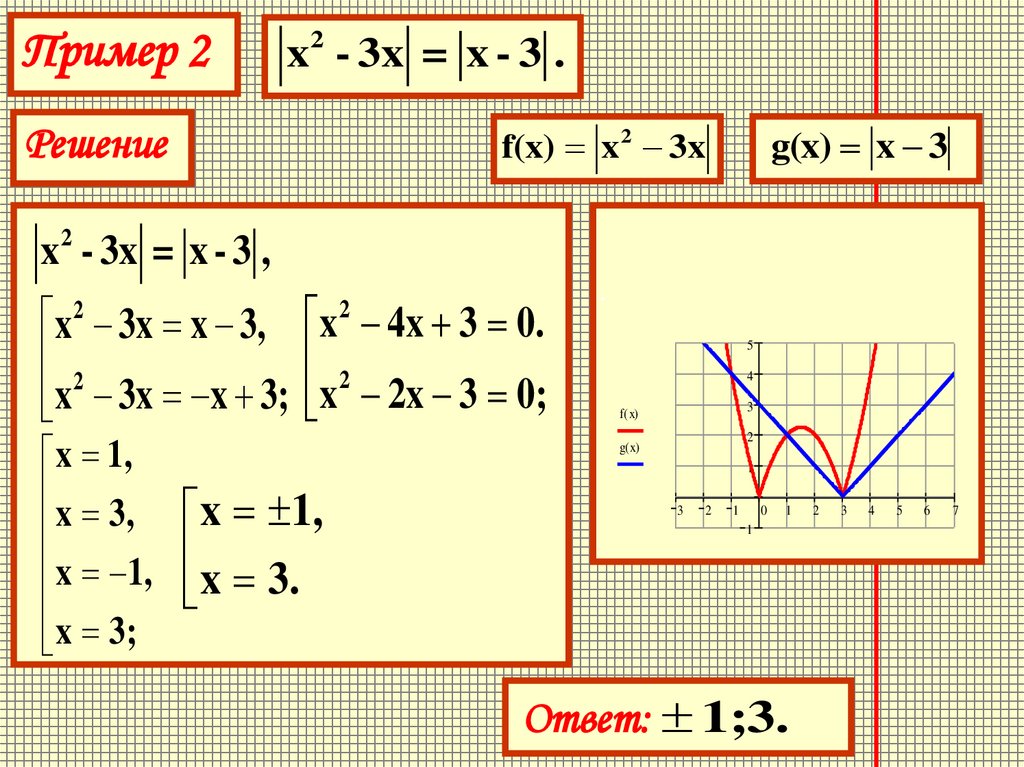
Пример 2
x 2 - 3x = x - 3 .
Решение
g(x) x 3
f(x) x 2 3x
x2 - 3x = x - 3 ,
2
x 3x x 3, x 4x 3 0.
2
2
x 3x x 3; x 2x 3 0;
2
x 1,
x 3,
x 1,
x 1, x 3.
x 3;
5
4
3
f( x)
2
g( x)
1
3
2
1
0
1
2
1
x
Ответ: 1;3.
3
4
5
6
7

11.

Алгоритм решения уравнений f(x) = g(x).
По определению
модуля уравнение
f(x) = g(x)
равносильно
совокупности
f(x) 0,
f(x) = g(x);
f(x) < 0,
f(x) = -g(x).
Уравнение
f(x) = g(x)
равносильно
смешанной системе
g(x) 0,
f(x) g(x),
f(x) g(x).

12.

Пример 1
Решение
x 2 2 3 x .
1
Ответ: x 1 .
3
x + 2 = 2 3 - x ,
3 x 0,
x 3,
x 2 2 3 x , x 2 6 2x,
x 2 2 3 x ;
x
x 2 6 2x;
x
x 3,
x 3,
1
3x
4,
x
x 1 ,
3
x 8;
x
x 8;
3,
1
1 ;
3
3,
8;
1
x 1 .
3

13.

Пример 2
x 2 x 3 x.(ЦТ 2004 г)
Решение
x 2 + x - 3 = x, x 0,
2
x x 3 x,
2
x 0,
x x 3 x;
x 3 ,
x
1,
x
3,
x 1;
x 3 .
x 0,
2
x 3 0,
2
x 2x 3 0;
Ответ: 1; 3 .

14.

Пример 3
x 3 x x 6.
2
Решение
x + 3 = x2 + x - 6,
x 3,
x 3 0,
x 3,
2
2
x 3;
x 3 x x 6; x 9 0;
x 3 0,
x 3,
x 3,
2
2
x 3 x x 6; x 2x 3 0; x 3, x 1;
Ответ:
x 3.
±3

15.

Пример 4
x2 4 x 1 5x 4 0. (ЦТ 2004 г)
Решение
x2 - 4 x +1 + 5x + 4 = 0,
x 1 0,
2
x 4 x 1 5x 4 0;
x 1 0,
x 2 4 x 1 5x 4 0;
x 1,
x 0, x 1;
x 1,
x 8, x 1;
x 1,
2
x 4x 4 5x 4 0;
x 1,
x 2 4x 4 5x 4 0;
x 1,
2
x x 0;
x 1,
x 2 9x 8 0;
x 1,
x 0,
x 8.
Ответ:
- 8;-1;0.

16.

Алгоритм решения уравнений
f1 (x) f2 (x) ... fn (x) g(x)
1. Найти нули всех подмодульных выражений,
расположить их по возрастанию на числовой оси и
выбрать крайний левый из полученных
интервалов.
2. .На полученных интервалах определить знак всех
подмодульных выражений и раскрыть модули по
определению.
3. Составить и решить совокупность смешанных
систем.

17.

Пример 1
x - 2 + x - 4 = 3.
Решение
Найдём нули под-
x - 2 = 0,
x - 4 = 0,
модульных выражений
x = 2.
x = 4.
+
+
+
x-2
x-4
-
-
2
-
4
Х

18.

Пример 1
x-2
x-4
Решение
-
x - 2 + x - 4 = 3.
+
2
-
4
+
+
Х
x < 2,
x < 2,
-x + 2 - x + 4 = 3; -2x + 6 = 3; x < 2,
2 x < 4,
2 x < 4, x = 1, 5;
x = 1, 5,
x 4, x = 4, 5.
x - 2 - x + 4 = 3; 2 = 3;
x = 4, 5;
x 4,
x 4,
x - 2 + x - 4 = 3; 2x - 6 = 3;

19.

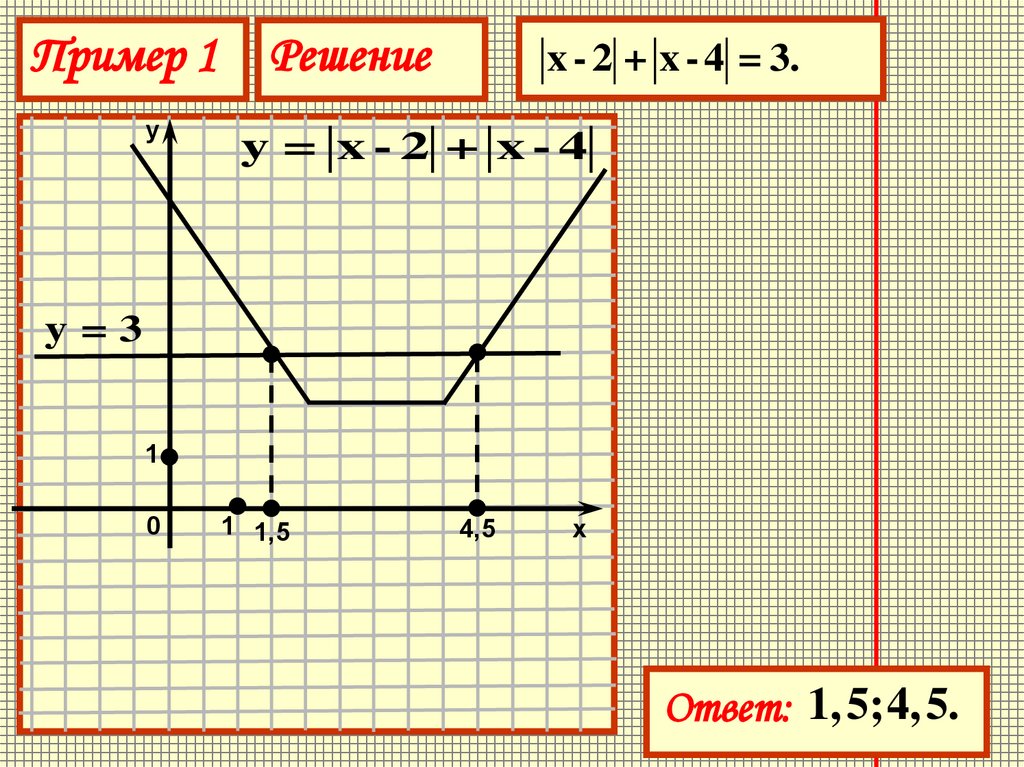
Пример 1
у
Решение
x - 2 + x - 4 = 3.
y = x-2 + x-4
y=3
1
0
1 1,5
4,5
х
Ответ: 1, 5;4, 5.

20.

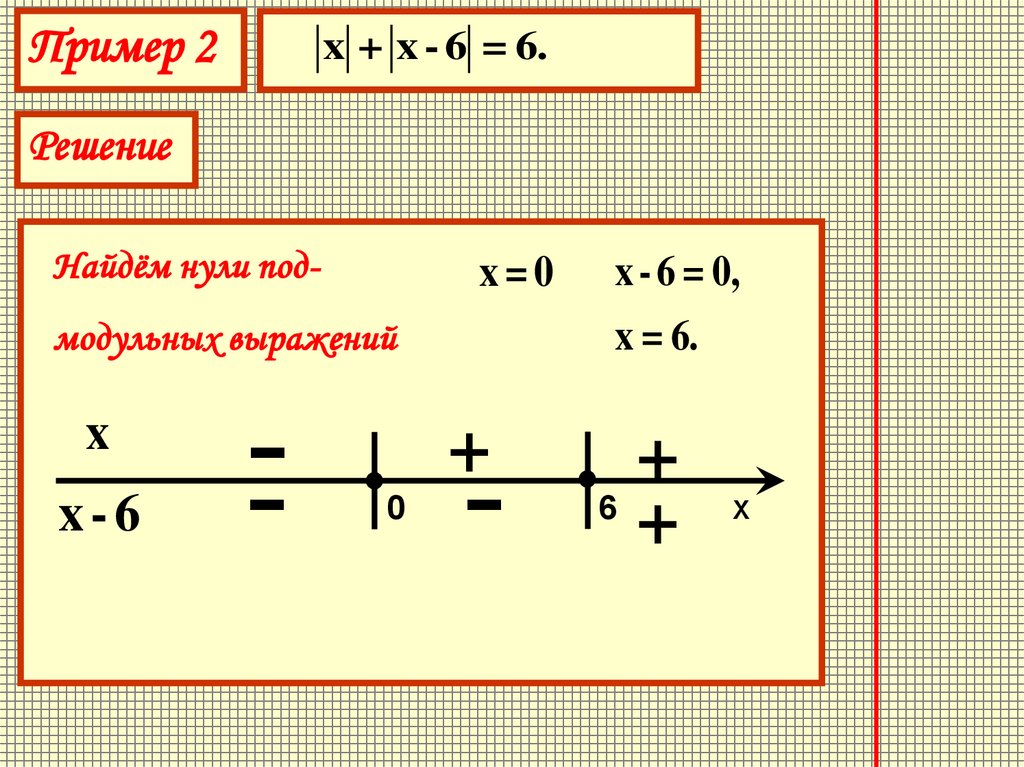
Пример 2
x + x - 6 = 6.
Решение
Найдём нули под-
x=0
модульных выражений
x
x-6
-
x = 6.
+
0
x - 6 = 0,
-
+
6
+
Х

21.

Пример 2
x
x-6
Решение
-
x + x - 6 = 6.
+
0
-
6
+
+
Х
x < 0,
x < 0,
x < 0,
-x
x
+
6
=
6;
2x = 0; x = 0;
0 x < 6,
0 x < 6, 0 x < 6,
x - x + 6 = 6; 6 = 6;
6 = 6;
x
6,
x 6,
x 6,
x
+
x
6
=
6;
2x = 12; x = 6;
0 x < 6,
x = 6;
0 x 6.

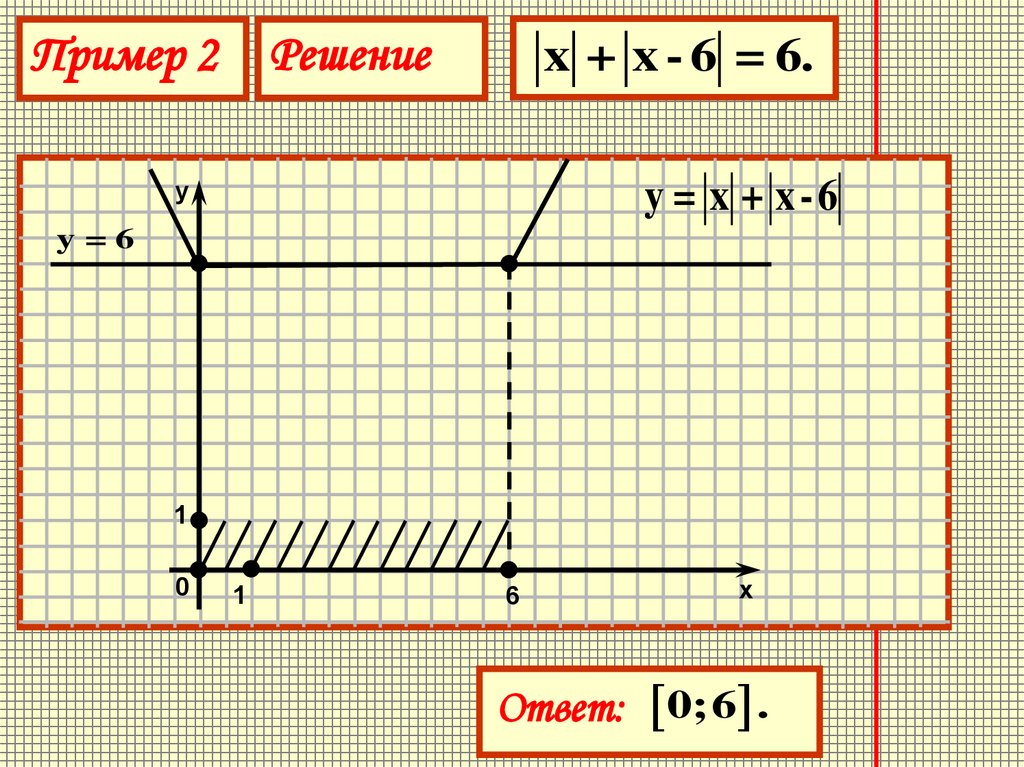
22.

Пример 2
Решение
x + x - 6 = 6.
у
y = x + x-6
y=6
1
0
1
6
х
Ответ: 0;6 .

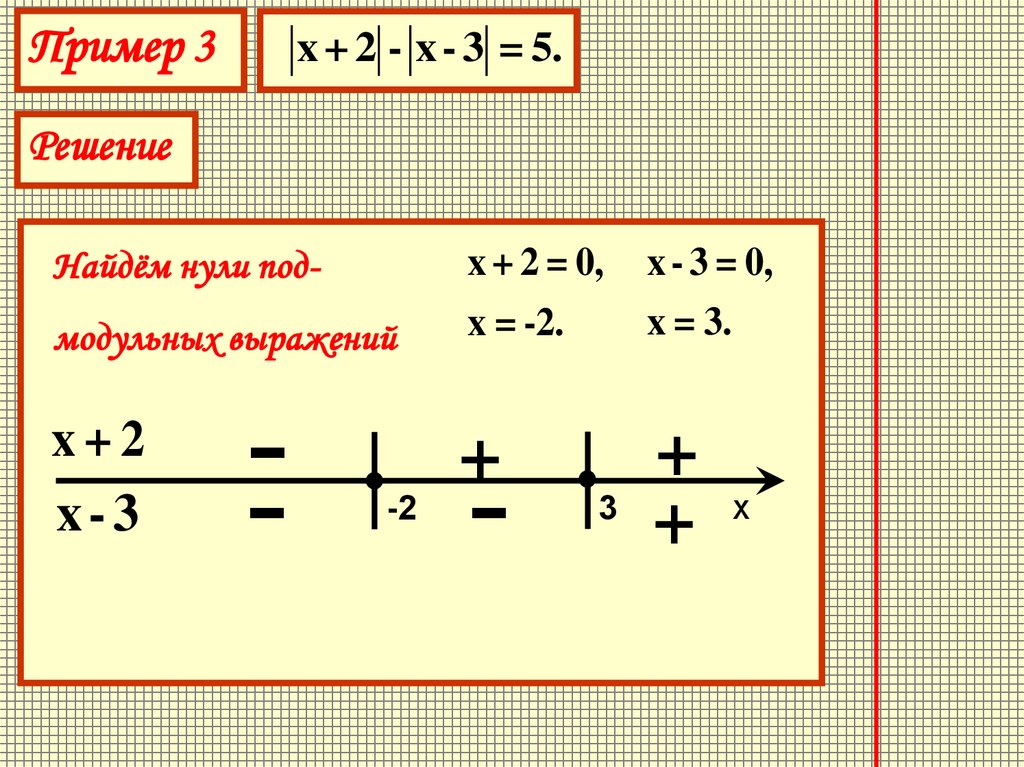
23.

Пример 3
x + 2 - x - 3 = 5.
Решение
Найдём нули под-
x + 2 = 0,
x - 3 = 0,
модульных выражений
x = -2.
x = 3.
+
+
+
x+2
x-3
-
-2
-
3
Х

24.

Пример 3
x+2
x-3
Решение
-
x < -2,
-x - 2 + x - 3 = 5;
-2 x < 3,
x + 2 + x - 3 = 5;
x 3,
x + 2 - x + 3 = 5;
x + 2 - x - 3 = 5.
+
-2
-
3
+
+
Х
x < -2,
-5 = 5;
-2 x < 3, -2 x < 3,
2x = 6; x = 3;
x 3;
x
3,
5 = 5;
x 3.

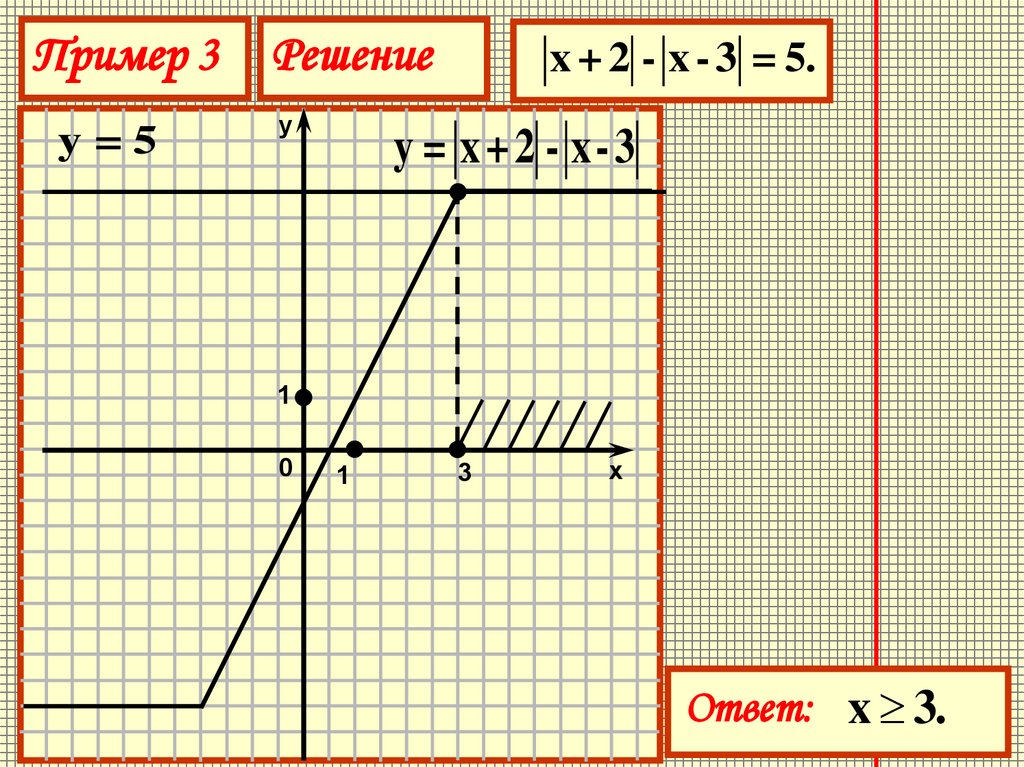
25.

Пример 3
y=5
Решение
у
x + 2 - x - 3 = 5.
y = x + 2 - x- 3
1
0
1
3
х
Ответ: x 3.

26.

Домашнее задание:
1) Материал лекции.
2) М.Л.Галицкий «Сборник задач по алгебре для 89 классов» §1п.6.
В помощь учащимся лицея-интерната при
СГАУ им. Н.И.Вавилова «Сборник задач по
математике. Часть I.» §5 стр. 74 ; 84.
3) М.Л.Галицкий «Сборник задач по алгебре для 89 классов» §5 №5.44в) ;5.44г) ; 5.52 ; 5.53.
В помощь учащимся лицея-интерната при
СГАУ им. Н.И.Вавилова «Сборник задач по
математике. Часть I.» §5 стр. 88 № 12 ; 18.