Similar presentations:
Решение уравнений, содержащих модуль
1.
Решение уравнений,содержащих модуль
Урок – практикум подготовки к ОГЭ по
алгебре, 9 класс
Автор: Морозова Надежда Павловна
учитель математики
МБОУ Пеновская СОШ
имени Е.И. Чайкиной
п.Пено
2. Цель урока
Решение различных типовуравнений с модулем
3. Ход урока
Фронтальный опросУстная работа
Обобщение и систематизация видов уравнений
с модулем
Итог урока
4. Определение модуля
Абсолютной величиной (модулем)действительного числа а называется само число а,
если оно ___________________, и число
противоположное а, если а__________________.
5. Определение модуля
Абсолютной величиной (модулем)действительного числа а называется само число
а, если оно не отрицательно , и число
противоположное а, если а__________________.
6. Определение модуля
Абсолютной величиной (модулем)действительного числа а называется само
число а, если оно не отрицательно , и число
противоположное а, если а отрицательное .
а
{
а, если а≥0
а, если а<0
7. Раскрыть модуль
1) |π – 3| =2) |√3 + √5|=
3) |1 - √2|=
4) |√5 – 2|=
5) |х4+1|=
6) |х2|=
7) | 3- √10 |=
8.
Раскрыть модуль1) |π – 3|= π – 3
2) |√3 + √5|=
3) |1 - √2|=
4) |√5 – 2|=
5) |х4+1|=
6) |х2|=
7) | 3- √10 |=
9.
Раскрыть модуль1) |π – 3|= π – 3
2) |√3 + √5|= √3 + √5
3) |1 - √2|=
4) |√5 – 2|=
5) |х4+1|=
6) |х2|=
7) | 3- √10 |=
10. Раскрыть модуль
1) |π – 3|= π – 32) |√3 + √5|= √3 + √5
3) |1 - √2|= √2 - 1
4) |√5 – 2|=
5) |х4+1|=
6) |х2|=
7) | 3- √10 |=
11. Раскрыть модуль
1) |π – 3|= π – 32) |√3 + √5|= √3 + √5
3) |1 - √2|= √2 - 1
4) |√5 – 2|= √5 – 2
5) |х4+1|=
6) |х2|=
7) | 3- √10 |=
12. Раскрыть модуль
1) |π – 3|= π – 32) |√3 + √5|= √3 + √5
3) |1 - √2|= √2 - 1
4) |√5 – 2|= √5 – 2
5) |х4+1|= х4+1
6) |х2|=
7) | 3- √10 |=
13.
Раскрыть модуль1) |π – 3|= π – 3
2) |√3 + √5|= √3 + √5
3) |1 - √2|= √2 - 1
4) |√5 – 2|= √5 – 2
5) |х4+1|= х4+1
6) |х2|= х2
7) | 3- √10 |=
14.
Раскрыть модуль1) |π – 3|= π – 3
2) |√3 + √5|= √3 + √5
3) |1 - √2|= √2 - 1
4) |√5 – 2|= √5 – 2
5) |х4+1|= х4+1
6) |х2|= х2
7) | 3- √10 |= √10- 3
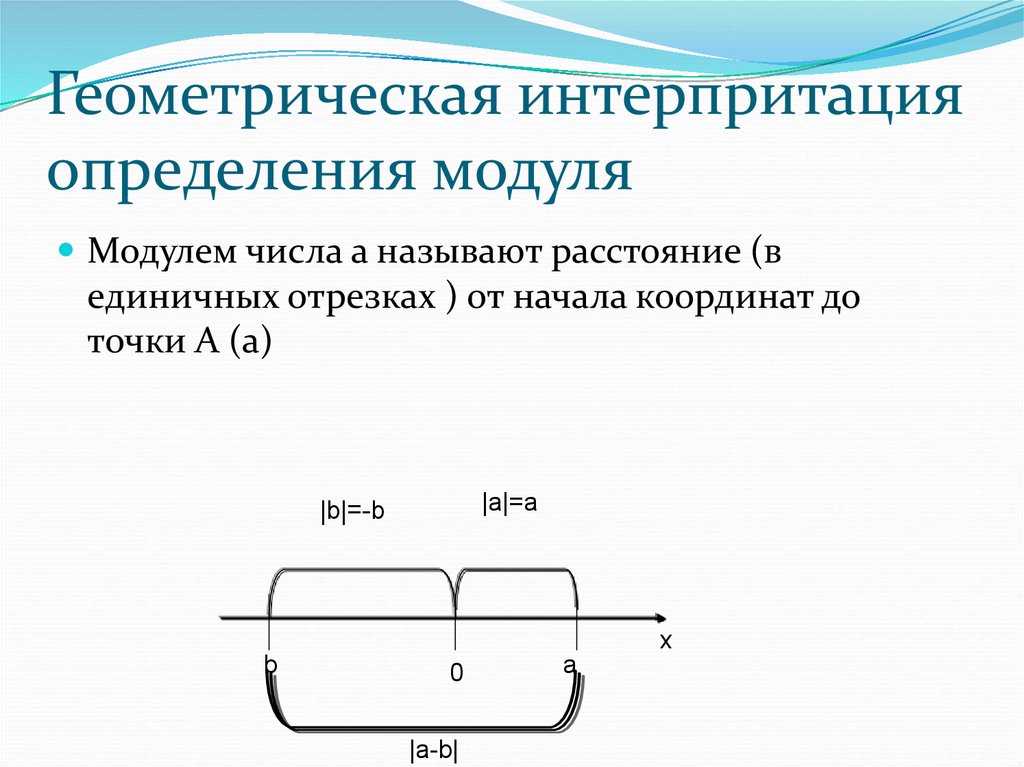
15. Геометрическая интерпритация определения модуля
Модулем числа а называют расстояние (вединичных отрезках ) от начала координат до
точки А (а)
|a|=a
|b|=-b
x
b
0
|a-b|
a
16. Различные типы уравнений с модулем
|ƒ(x)|=a, а≥0|ƒ(x)|=g(x)
ƒ(|x|)=а
|ƒ(x)|=|g(x)|
|ƒ1(x)|+|ƒ2(x)|+…+|ƒn(x)|=g(x)
17. Уравнения с модулем из сборников заданий для подготовки к ОГЭ в 9 классе
х₂ - |х|- 6 =0|2х-3|=4
|х8|=5
|х₂х8|=х
8|х|=0
|3х+5|=6
|2х-3|=3-2x
|x+1|=3(2-x)
2|х-2|-3|x+4|=1
|3х-4|=4х2+3х-5
18.
Уравнение вида|ƒ(x)|=a, а≥0
Распадается на совокупность двух уравнений:
ƒ(x)=a
ƒ(x)=-a
19. Пример 1
Решить уравнение |х-8|=5По определению модуля имеем совокупность уравнений
Х-8=5
Х-8=-5.
Откуда х=13, х=3.
Ответ: 3;13.
Некоторые уравнения и неравенства с модулем решаются проще с
помощью геометрических
соображений. |a-b|-это расстояние между a и b.
Решим предыдущее уравнение |х-8|=5.
3
Ответ: 3;13.
8
13
x
20. Пример 2
Решить уравнение|2х-3|=4
2 x 3 4
2x 3 4
2 x 3 4,
x 3,5
x 0,5
Решение на основе геометрической интерпретации
-1
3
7
x
На расстоянии 4 от 3 лежат две точки -1 и 7, а 2х есть одна из
них.
Следовательно, 2х=-1, или 2х=7,
Х=-0,5. Х=3.5
Ответ: -0.5; 3,5.
21. |ƒ(x)|= g(x)
Уравнение вида|ƒ(x)|= g(x)
Равносильно совокупности двух систем
ƒ(x)= g(x),
g(x) ≥0;
ƒ(x)= -g(x),
g(x) ≥0.
22. Пример 1
Решить уравнение |2х-3|=3-2xРешение
|2х-3|=-(2x-3)
Воспользуемся следующим фактором:
|ƒ(x)|= -ƒ(x), если ƒ(x)≤0.Тогда данное
уравнение равносильно неравенству
2x-3 ≤0, х ≤ 3/2
Ответ: (-∞; 3/2]
23. Уравнение вида
f (|x|)=аРаспадается на совокупность двух систем
f(х)=а;
х≥0,
F(-х)=а;
х≤0
24. Пример 1
Решить уравнение х2-|х|-6=0Данное уравнение равносильно совокупности двух систем:
x 0,
1) 2
x x 6 0;
x 0,
2) 2
x x 6 0.
Решим первую систему уравнений
x 0,
x 3; x 2
x 3
Решим вторую систему уравнений
x 0,
x 3; x 2
Ответ: -3;3.
x 3
25. Уравнение вида
|f1(x)|+ |f2(x)|+…+ |fn(x)|=g(x)Алгоритм решения:
Пусть дано уравнение F(x)=0 такое, что его левая часть содержит модули
некоторых функций
|f1(x)|, |f2(x)|,…, |fn(x)|
Решают каждое из уравнений f1(x)=0, f2(x)=0,…fn(x)=0
Вся координатная ось разбивается на некоторое число промежутков.
На каждом таком промежутке уравнение заменяется на другое уравнение,
не содержащее знаков модуля и равносильно исходному уравнению на
этом промежутке.
На каждом промежутке отыскиваются корни того уравнения, которое на
этом промежутке получается.
Отбираются те корни, которые принадлежат данному промежутку. Они и
будут корнями исходного уравнения на рассматриваемом промежутке.
Все корни уравнения F(х)=0 получают, объединяя все корни, найденные
на всех промежутках.
26. Пример 1
Решить уравнение 2|х-2|-3|x+4|=1Решение
Для освобождения от знаков модуля разобьем числовую прямую на
три промежутка
-4
2
х
Решение данного уравнения сводится к решению трех систем:
x 4
x 4
1.
x 15
2( x 2) 3( x 4) 1 x 15
4 x 2
4 x 2
2.
x 1,8
2 x 4 3x 12 1 x 1,8
x 2
x 2
3.
x 17
2 x 4 3x 12 1 x 17
Ответ: -15; -1.8
27. Итог урока
Повторили определение модуляРассмотрели примеры различных типов
уравнений с модулем
28. Список используемых источников
ЛитератураМатематика. Подготовка к ОГЭ –2019Под ред.Ф.Ф.
Лысенко, С.О. Иванова. – Ростов – на – Дону.:
Легион, 2018
8-9 классы: сборник элективных курсов / авт. –
сост. В.Н. Студенецкая, Л.С. Сагателова. –
Волгоград: Учитель, 2013.



























 mathematics
mathematics








