Similar presentations:
Модуль и его приложения
1.
МОУ «Школа №9 г. Тореза»Модуль и его
приложения
Расчитано на 2 урока
(20.05 и 21.05)
9 класс
Пономарёва Светлана
Владимировна
2. 20.05.Понятие модуля
20.05.ПОНЯТИЕ МОДУЛЯАбсолютной величиной (модулем)
действительного числа а называется само
число а, если оно неотрицательное, и число,
противоположное а, если а – отрицательное.
a , если а 0;
a
а , если а 0.
Пример:
2x 3, если x 1,5;
2x 3
2x 3, если x 1,5.
3. Свойства модуля
СВОЙСТВА МОДУЛЯ1 a а
2 a b а b
а
a
3
, где b 0
b
b
4 a b а b , если a 0, b 0
5 a b a b, если a 0, b 0
4. Свойства модуля
СВОЙСТВА МОДУЛЯ6 a b а b , если ab 0
7 a
2
a
2
8 a b 0, если a b 0
2
9
2
a а
2
10 a1 a2 ... an а1 а2 ... аn
5. Геометрическая интерпретация модуля
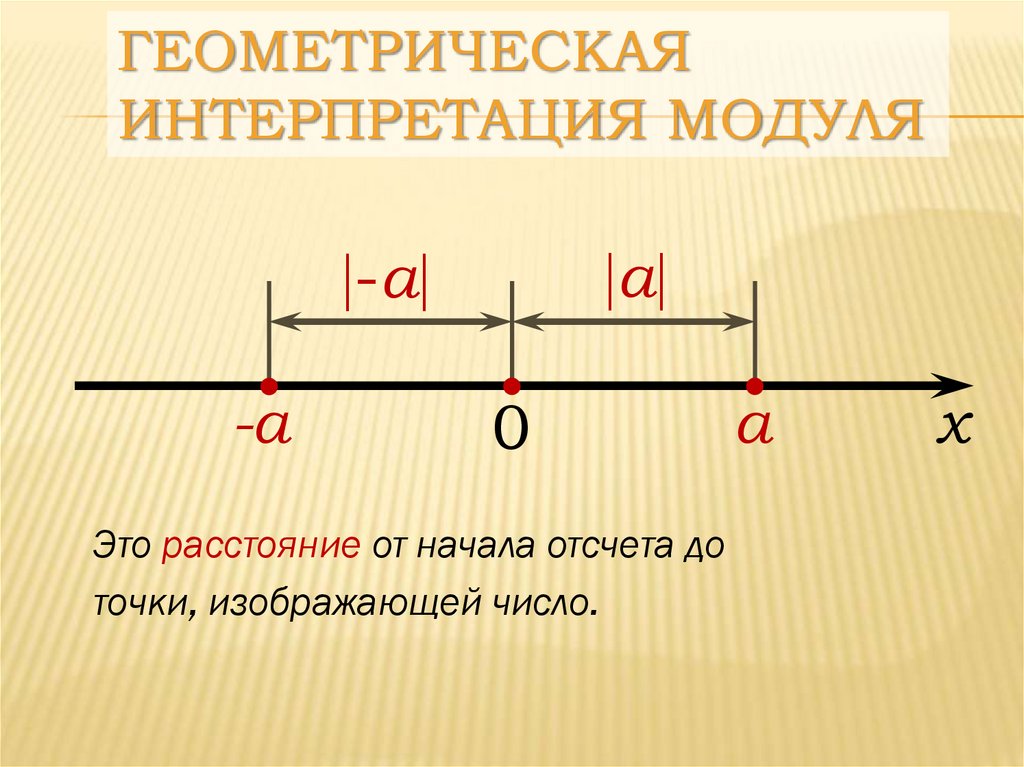
ГЕОМЕТРИЧЕСКАЯИНТЕРПРЕТАЦИЯ МОДУЛЯ
а
-а
-а
0
Это расстояние от начала отсчета до
точки, изображающей число.
а
х
6. Примеры Раскрыть модули:
ПРИМЕРЫРАСКРЫТЬ МОДУЛИ:
1) p 3 ;
2)
3 5;
3)
5 2;
4) 1 2 ;
5) x 2 ;
6) x 1 ;
4
7) ( a 3 ) , a 3 ;
2
8) ( b 4 ) , b 4 ;
2
9) m 2m 1,
2
m 1.
7. Решение уравнений вида f(x)= a
РЕШЕНИЕ УРАВНЕНИЙВИДА
F(X) = A
f (x ) a ,
f (x ) a.
Пример: x – 8 =5
x 8 5,
x 13,
x 8 5; ⇔
x 3.
Ответ: 3; 13.
8. Решение уравнений вида |f(x)|= a
РЕШЕНИЕ УРАВНЕНИЙВИДА
|F(X)|= A
|2x – 3|= 4
|5x + 6|= 7
|9 – 3x |= 6
|4x + 2|= – 1
|8 – 2x|= 0
|10x + 3|= 16
|24 – 3x|= 12
|2x + 30|= 48
x1 = 3,5;
x1 = 0,2;
x1 = 1;
x Ø
x=4
x1 = 1,3;
x1 = 12;
x1 = 9;
x2 = – 0,5
x2 = – 2,6
x2 = 5
x2 = – 1,9
x2 = 4
x2 = – 39
9.
Решение уравнений видаf(x) = g(x)
f (x ) g (x ),
g
(
x
)
0
;
f (x ) g (x ),
g (x ) 0.
или
f (x ) g (x ),
f (x ) g (x ),
g (x ) 0;
10. Пример: 3х –10 = х – 2
ПРИМЕР: 3Х –10 = Х – 23x 10 x 2,
x
2
0
;
3x 10 (x 2), ⇔
x 2 0;
x 4,
⇔
x 3.
2x 8,
x
2
;
⇔
4x 12,
x 2;
Ответ: 3; 4.
11.
Решение уравнений видаf(x) = g(x)
f (x ) g (x ),
f (x ) g (x ).
Пример: x – 2 = 3 – x
x 2 3 x ,
x 2 3 x ;
⇔
2x 5,
2 3;
Ответ: 2,5.
x 2,5,
⇔ x Ø ;
12. Решить самостоятельно: 4x –1 = 2х + 3
РЕШИТЬ САМОСТОЯТЕЛЬНО:4X –1 = 2Х + 3
x 2,
4x 1 2x 3,
2x 4,
⇔
1
4x 1 2x 3; ⇔ 6х 2;
x .
3
1
Ответ: 2; – ---.
3
13. Решить уравнение 2|x – 2| – 3|х + 4| = 1
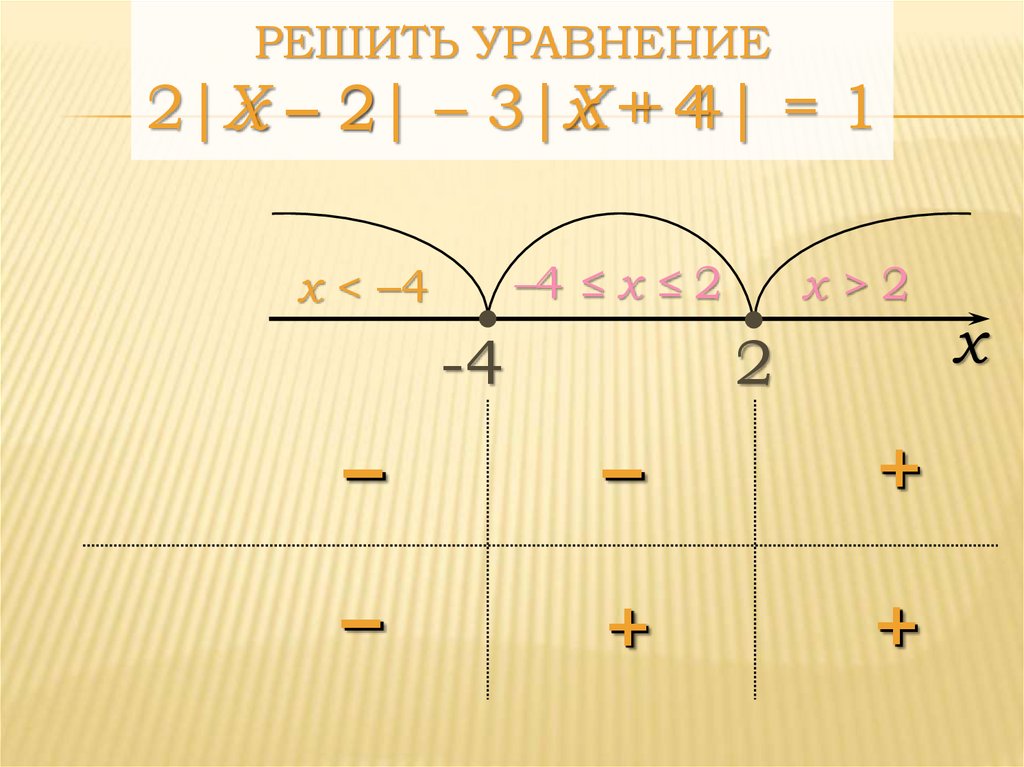
РЕШИТЬ УРАВНЕНИЕx ++ 44| = 1
2|X
2| – 3|Х
x–2
–4 ≤ x ≤ 2
x < –4
-4
x>2
2
–
–
+
–
+
+
х
14. Решить уравнение 2x – 2 – 3х + 4 = 1
РЕШИТЬ УРАВНЕНИЕ2 X – 2 – 3 Х + 4 = 1
x 4,
2( x 2) 3( x 4) 1;
4 x 2,
2( x 2) 3(x 4) 1;
x 2,
2(x 2) 3(x 4) 1;
⇔
x 4,
x 15;
4 x 2,
x 1,8;
x 2,
x 17.
Ответ: –15; –1,8.
15. Примеры (решить самостоятельно)
ПРИМЕРЫ(РЕШИТЬ САМОСТОЯТЕЛЬНО)
1) x2 + 3x = 2(x + 1)
2) x – 6 = x2 – 5x + 9
3) 2x + 8 – x – 5 = 12
1) Ответ: 1; (–5 + √17)/2.
2) Ответ: 1; 3.
3) Ответ: [2; + )
16. 21.05. Решение неравенства вида x а
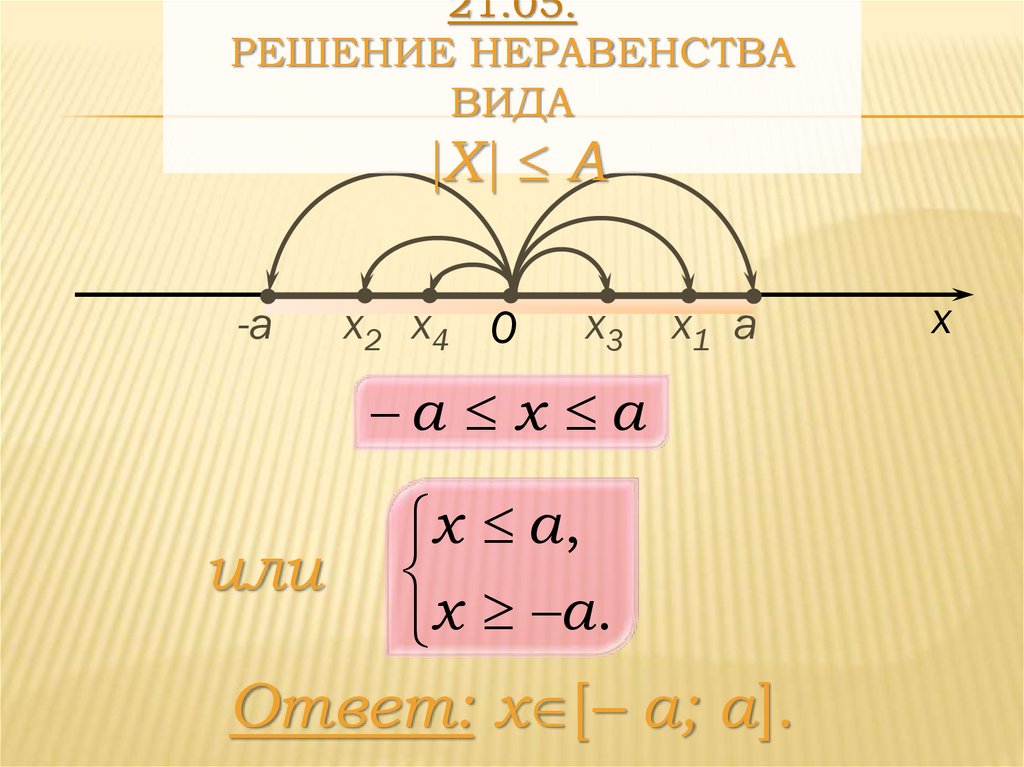
21.05.РЕШЕНИЕ НЕРАВЕНСТВА
ВИДА
X А
-а
х2 х4 0
х3
х1 а
a x a
или
x a ,
x a.
Ответ: x [– а; a].
х
17. Решение неравенства вида f(x) а
РЕШЕНИЕ НЕРАВЕНСТВАВИДА
F(X) А
a f (x ) a
Пример: x – 5 ≤ 7
+5
–7≤x–5≤7
–7+5≤x–5+5≤7+5
– 2 ≤ x ≤ 12
Ответ: [– 2; 12]
18.
Решите самостоятельно:5x + 8 < 12
– 12 < 5x + 8 < 12
–8
– 12 – 8 < 5x + 8 – 8 < 12 – 8
– 20 < 5x < 4
– 20 : 5 < 5x : 5 < 4 : 5
– 4 < x < 0,8
Ответ: (– 4; 0,8).
19. Решение неравенства вида x а
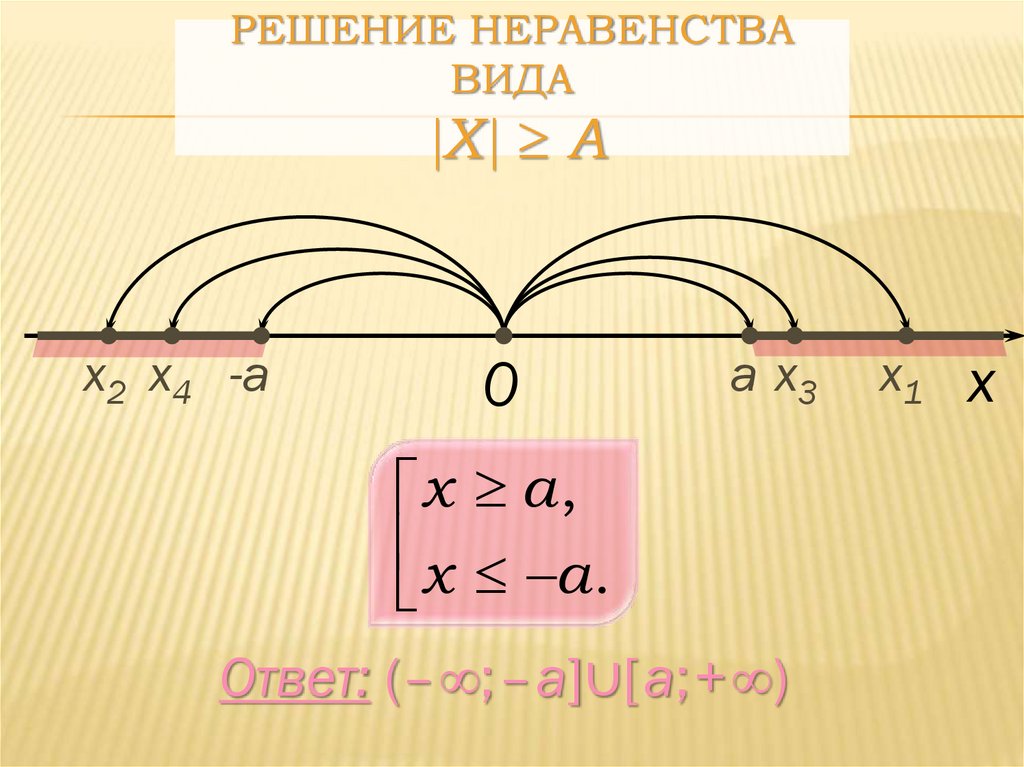
РЕШЕНИЕ НЕРАВЕНСТВАВИДА
X А
х2 х4 -а
0
а х3
x a ,
x a.
Ответ: (–∞;–a]∪[a;+∞)
х1
х
20. Решение неравенства вида f(x) а
РЕШЕНИЕ НЕРАВЕНСТВАВИДА
F(X) А
f (x ) a ,
f (x ) a.
Пример: x + 4 ≥ 6
x+4≥6
x+4≤–6
⇔
x≥2
x ≤ – 10
Ответ: (–∞;–10]∪[2;+∞)
21.
Решите самостоятельно:10x – 7 > 19
10x 7 19,
10x 26,
⇔
⇔
10x 7 19;
10x 12;
x 2,6,
⇔
x 1,2;
Ответ: (–∞;–1,2)∪(2,6;+∞)
22. Решить неравенство 3x – 2 + х – 6 8
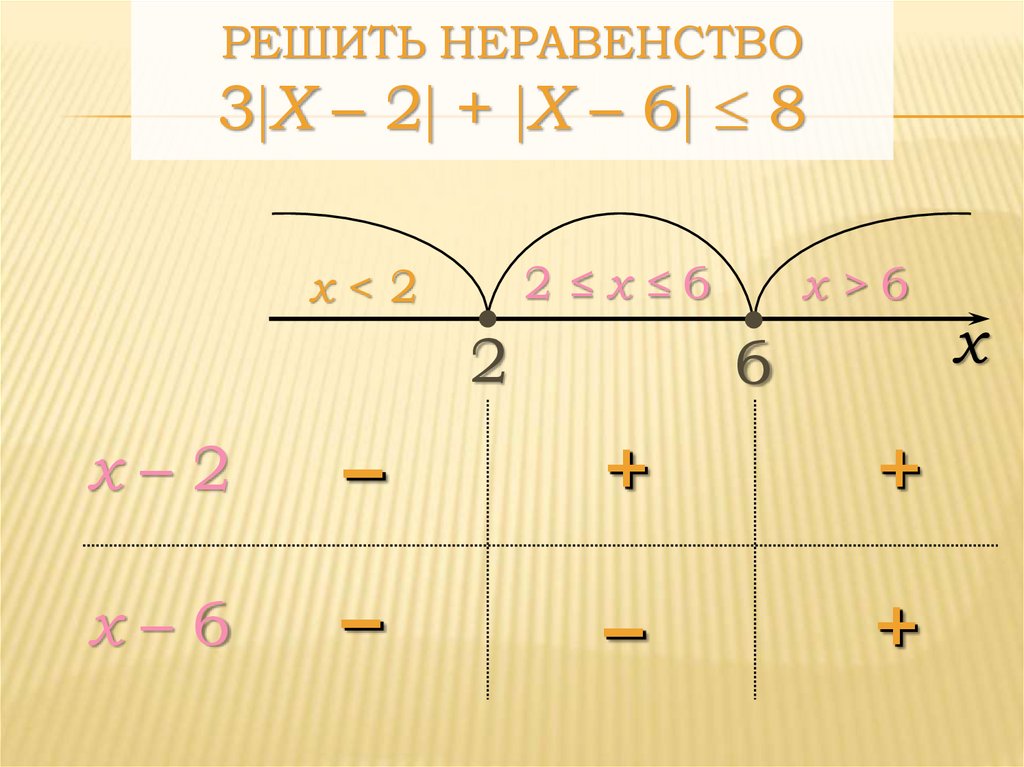
РЕШИТЬ НЕРАВЕНСТВО3 X – 2 + Х – 6 8
2≤x≤6
x<2
2
x>6
6
x–2
–
+
+
х–6
–
–
+
х
23. Решить неравенство 3x – 2 + х – 6 8
РЕШИТЬ НЕРАВЕНСТВО3 X – 2 + Х – 6 8
x 2,
3( x 2) ( x 6) 8;
2 x 6,
3(x 2) ( x 6) 8;
x 6,
3(x 2) (x 6) 8;
⇔
x 2,
4x 4;
2 x 6,
2x 8;
x 6,
4x 20;
⇔
24. Решить неравенство 3x – 2 + х – 6 8
РЕШИТЬ НЕРАВЕНСТВО3 X – 2 + Х – 6 8
⇔
x 2,
x 1;
2 x 6,
x 4;
x 6,
x 5.
⇔
1 x 2,
2 x 4,
x .
Ответ: [1; 4].
25. Построение графика функции y = x
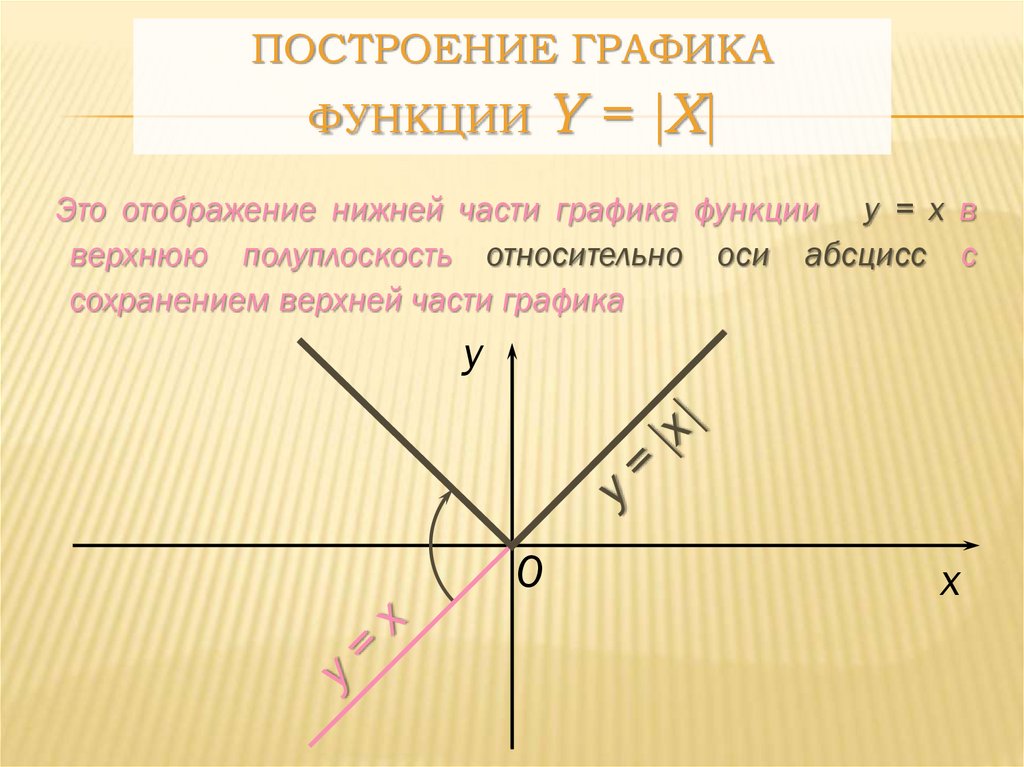
ПОСТРОЕНИЕ ГРАФИКАФУНКЦИИ
Y = X
Это отображение нижней части графика функции y = x в
верхнюю полуплоскость относительно оси абсцисс с
сохранением верхней части графика
y
0
x
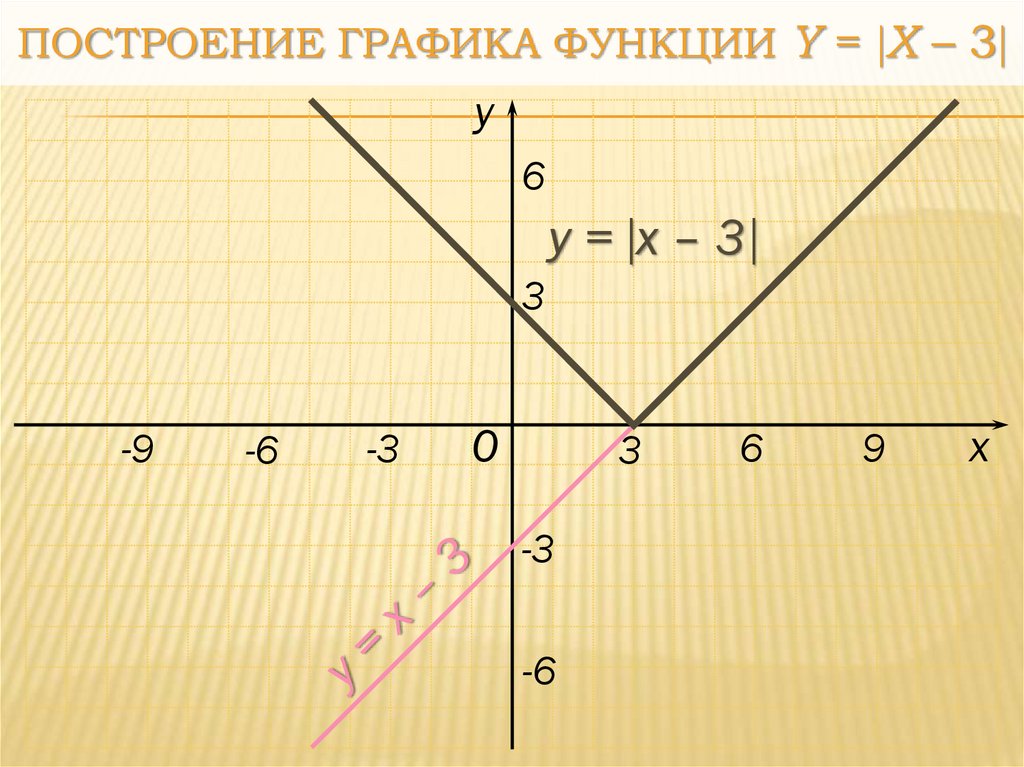
26. Построение графика функции y = x – 3
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = X – 3y
6
y = x – 3
3
-9
-6
-3
0
3
-3
-6
6
9
x
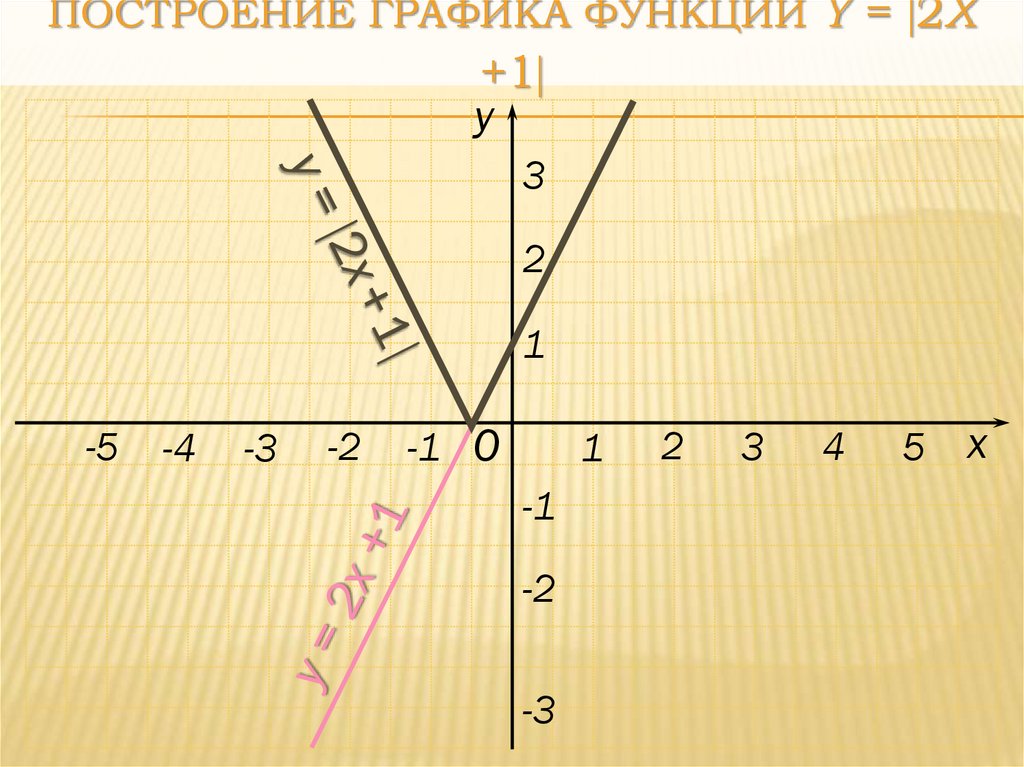
27. Построение графика функции y = 2x +1
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ Y = 2X+1
y
3
2
1
-5
-4
-3
-2
-1 0
1
-1
-2
-3
2
3
4
5
x
28.
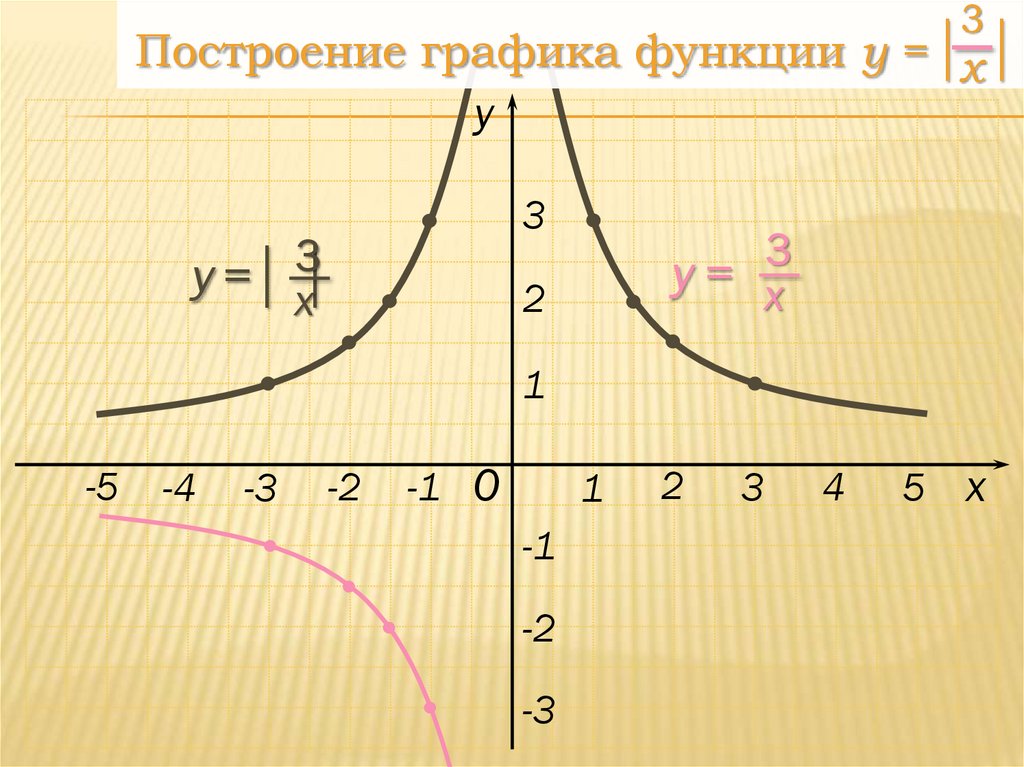
3Построение графика функции y = х
y
3
3
y = х
3
y= х
2
1
-5
-4
-3
-2
-1 0
1
-1
-2
-3
2
3
4
5
x
29.
Построение графика функцииy = x + 2 – x – 3
x < -2
-2 ≤ x ≤ 3
--2
x>3
3
x+2
–
+
+
x–3
–
–
+
x
30.
Построение графика функцииy = x + 2 – x – 3
x 2,
y x 2 x 3;
2 x 3,
y x 2 x 3;
x 3,
y x 2 x 3;
⇔
x 2,
y 5;
2 x 3,
y 2x 1;
x 3,
y 5.
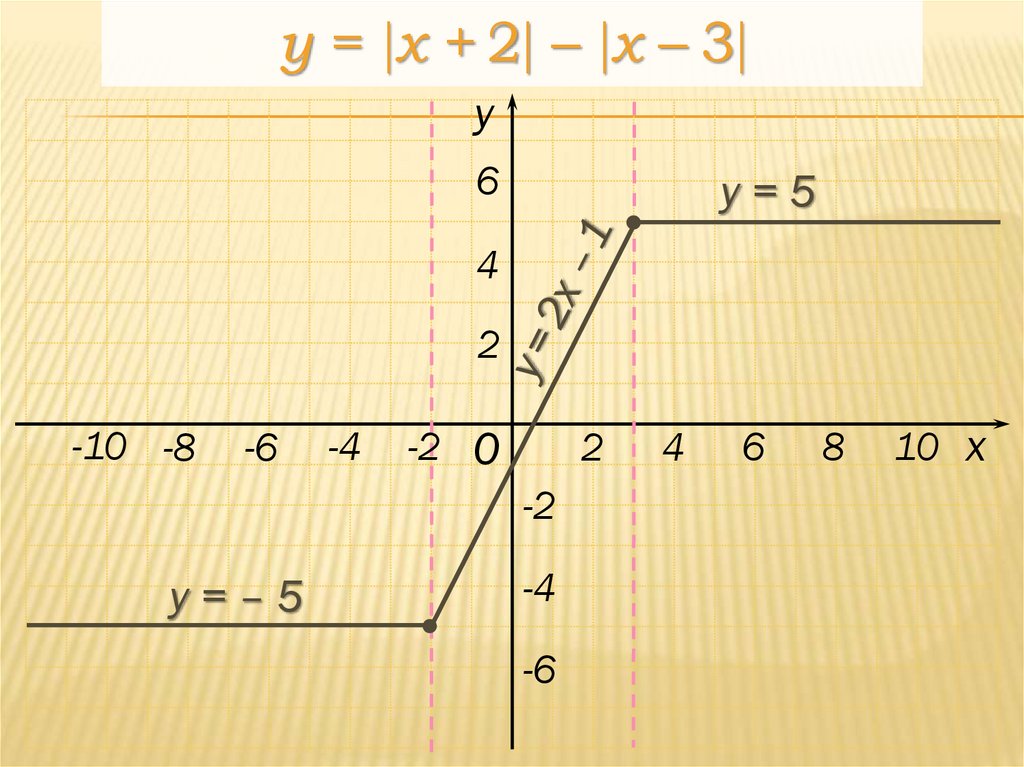
31.
y = x + 2 – x – 3y
6
у=5
4
2
-10 -8
-6
-4
-2 0
2
-2
у=–5
-4
-6
4
6
8
10 x
32.
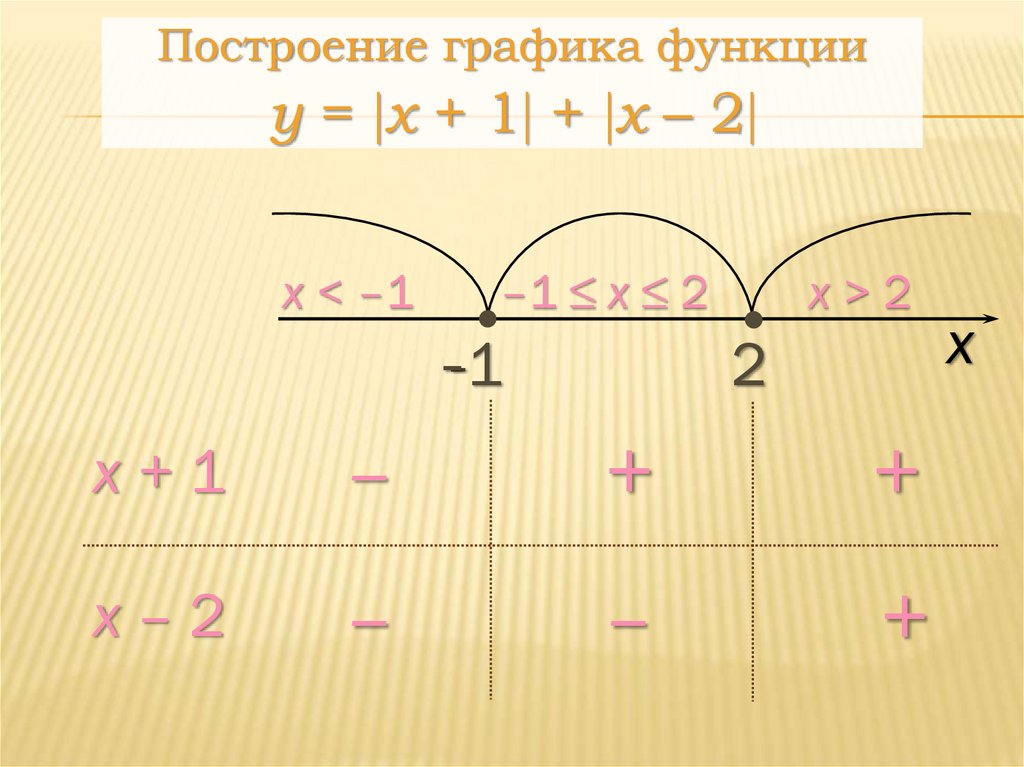
Построение графика функцииy = x + 1 + x – 2
x < –1
–1 ≤ x ≤ 2
--1
x>2
2
x+1
–
+
+
x–2
–
–
+
x
33.
Построение графика функцииy = x + 1 + x – 2
x 1,
y x 1 x 2;
1 x 2,
y x 1 x 2;
x 2,
y x 1 x 2;
⇔
x 1,
y 2x 1;
1 x 2,
y 3;
x 2,
y 2x 1.
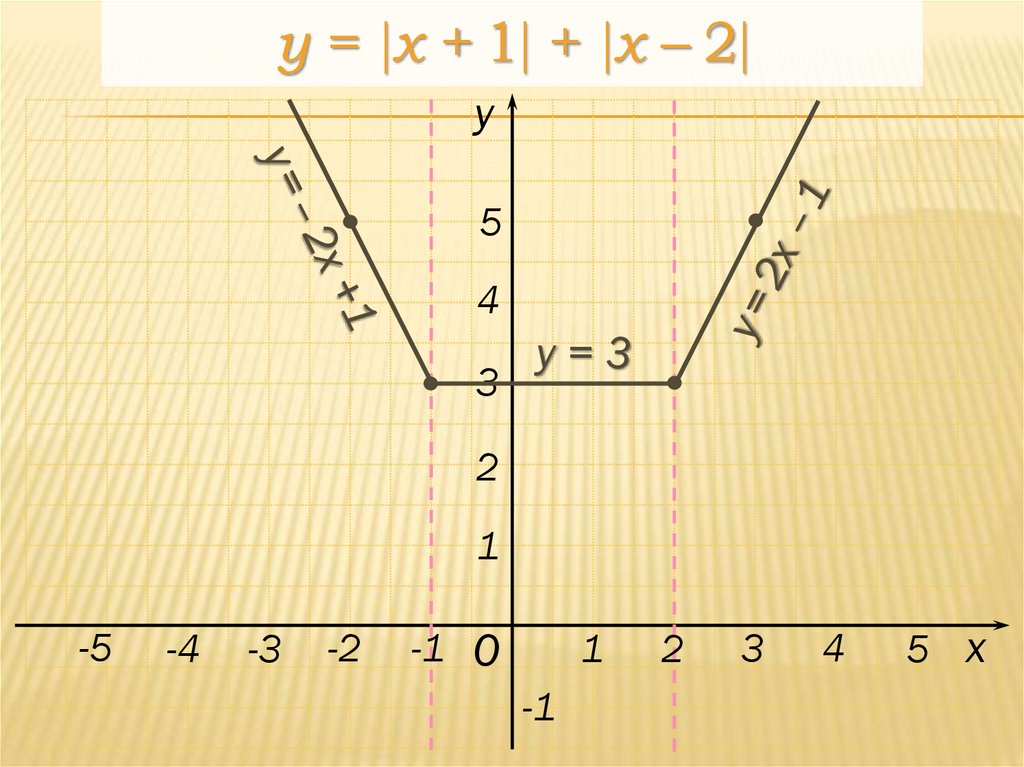
34.
y = x + 1 + x – 2y
5
4
3
у=3
2
1
-5
-4
-3
-2
-1 0
1
-1
2
3
4
5 x
35. Домашнее задание:
ДОМАШНЕЕ ЗАДАНИЕ:Просмотрите презентацию.
Разберите решение уравнений и неравенств
с модулем.























 mathematics
mathematics








