Similar presentations:
Графическое решение уравнений, содержащих неизвестную величину под знаком модуля
1. Графическое решение уравнений, содержащих неизвестную величину под знаком модуля.
Комлева Ольга Николаевна,г. Чайковский,
лицей «Синтон»
2010 год
2. Определение:
Модуль числа a или абсолютнаявеличина числа a равна a, если a больше
или равно нулю и равна -a, если a
меньше нуля:
a, если a 0;
| a|
a, если a 0.
3.
Решение уравнений видаf ( x) c
f ( x) g ( x) c
f ( x) g ( x) c
f ( x) g ( x)
с помощью графиков функций
y f ( x) , y f ( x) g ( x) ,
y f ( x) g ( x) , y c
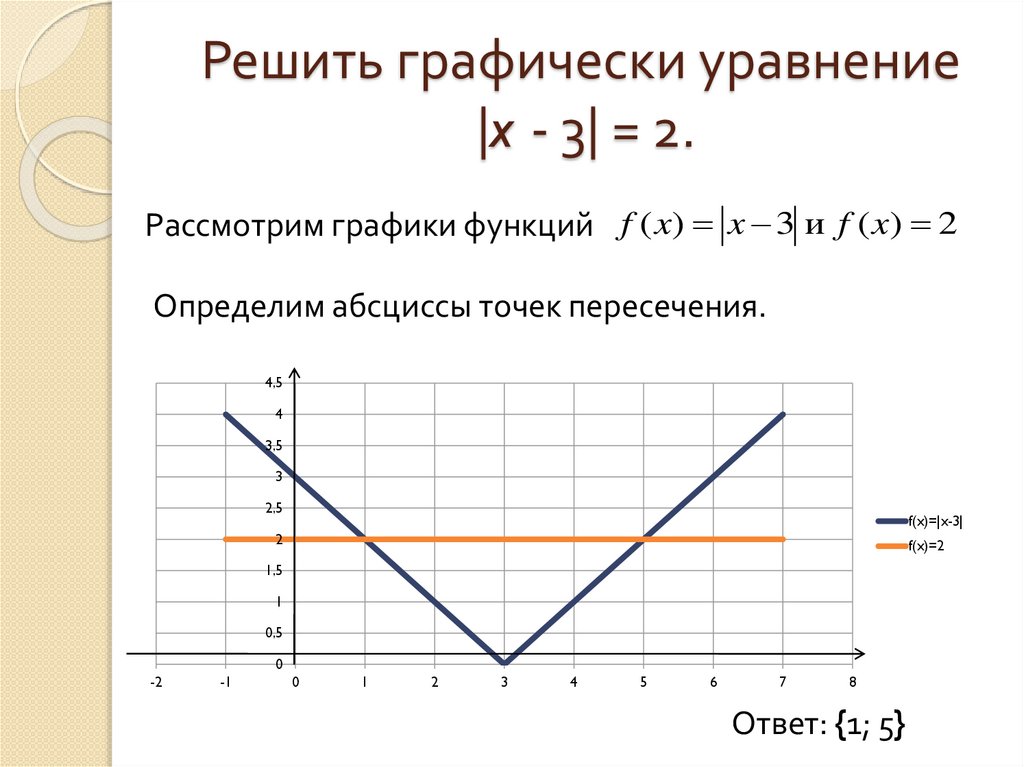
4. Решить графически уравнение |x - 3| = 2.
Рассмотрим графики функций f ( x) x 3 и f ( x) 2Определим абсциссы точек пересечения.
4,5
4
3,5
3
2,5
f(x)=|x-3|
2
f(x)=2
1,5
1
0,5
0
-2
-1
0
1
2
3
4
5
6
7
8
Ответ: {1; 5}
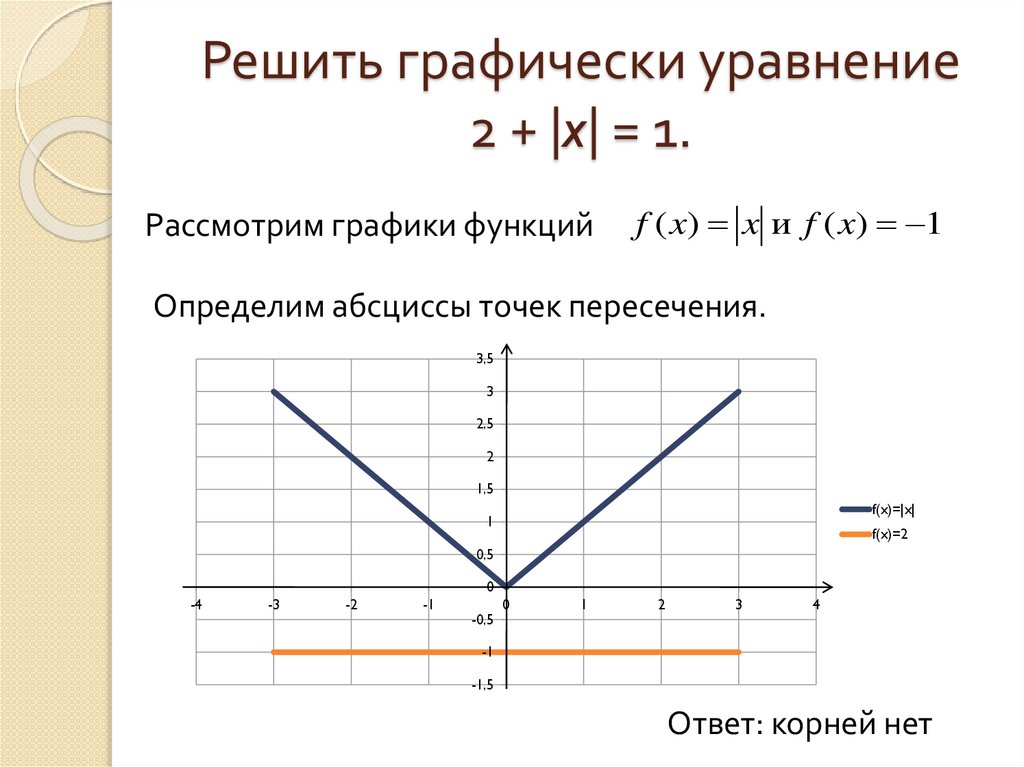
5. Решить графически уравнение 2 + |x| = 1.
Рассмотрим графики функцийf ( x) x и f ( x) 1
Определим абсциссы точек пересечения.
3,5
3
2,5
2
1,5
f(x)=|x|
1
f(x)=2
0,5
0
-4
-3
-2
-1
-0,5
0
1
2
3
4
-1
-1,5
Ответ: корней нет
6. Решить графически уравнение |-x + 2| = 2x + 2.
12Рассмотрим графики функций
10
f ( x) x 2 и f ( x) 2 x 2
8
Определим абсциссы
точек пересечения.
6
f(x)=|-x+2|
f(x)=2x+2
4
2
Ответ: {0}
0
-2
-1
0
1
2
3
4
5
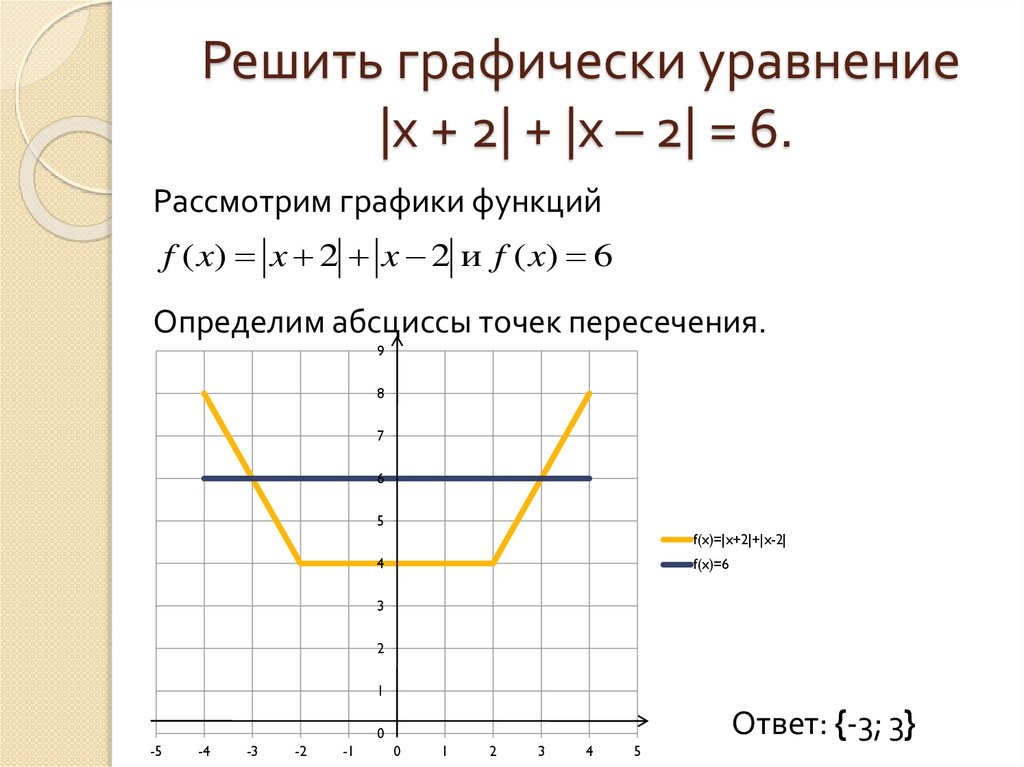
7. Решить графически уравнение |x + 2| + |х – 2| = 6.
Рассмотрим графики функцийf ( x) x 2 x 2 и f ( x) 6
Определим абсциссы точек пересечения.
9
8
7
6
5
f(x)=|x+2|+|x-2|
4
f(x)=6
3
2
1
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
Ответ: {-3; 3}
8. Решить графически уравнение | x | – | х – 1| = 0,5 – х.
Рассмотрим графики функцийf ( x) x x 1 и f ( x) 0,5 x
4
3
2
1
f(x)=|x|-|x-1|
0
-4
-3
-2
-1
0
1
2
3
4
5
f(x)=0,5-x
-1
-2
-3
-4
Ответ: {0,5}
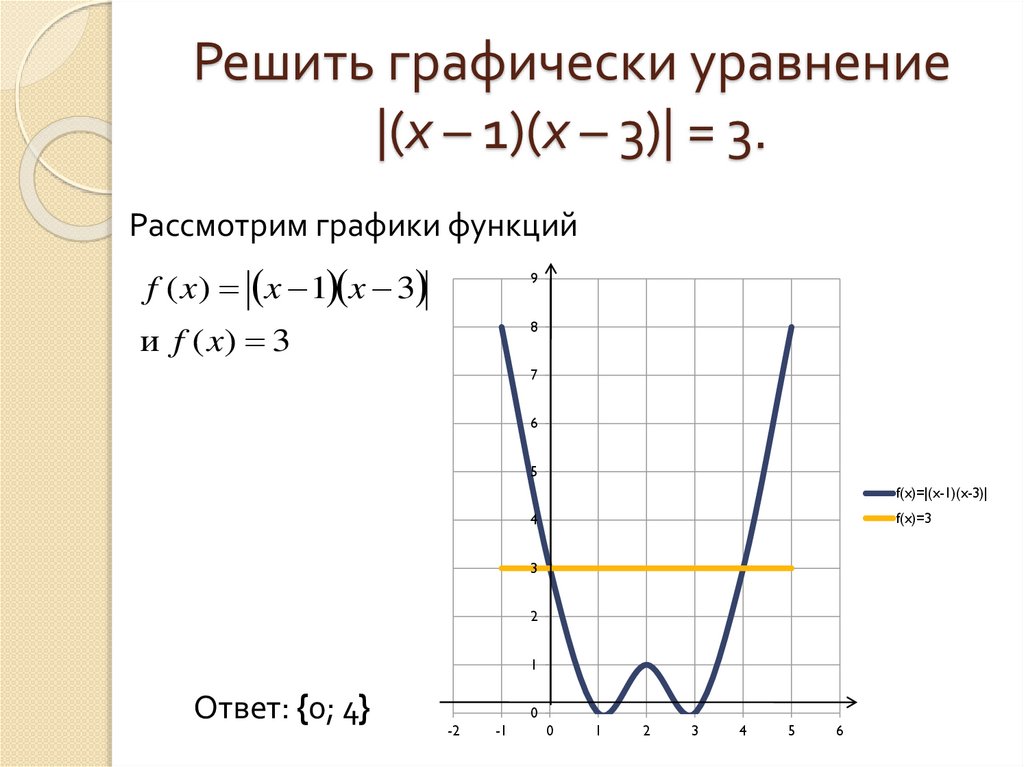
9. Решить графически уравнение |(x – 1)(x – 3)| = 3.
Рассмотрим графики функцийf ( x) x 1 x 3
9
8
и f ( x) 3
7
6
5
f(x)=|(x-1)(x-3)|
f(x)=3
4
3
2
1
Ответ: {0; 4}
0
-2
-1
0
1
2
3
4
5
6
10. Графический метод решения уравнений красив, но не идеален:
графики уравнений не всегда можнопостроить;
точки пересечения могут быть не
такими «хорошими», как в показанных
примерах, или оказаться за пределами
чертежа






 mathematics
mathematics








