Инструкция по определению числовых характеристик выборки

1. ИНСТРУКЦИЯ ПО ОПРЕДЕЛЕНИЮ ЧИСЛОВЫХ ХАРАКТЕРИСТИК ВЫБОРКИ

2. ДИСКРЕТНЫЙ ВАРИАЦИОННЫЙ РЯД

По данным выборки:
1. Составить дискретный вариационный ряд.
2. Найти средние характеристики:
а) среднее выборочное x ;
б) моду Mo;
в) медиану Me.
3. Найти характеристики вариации:
а) размах вариации XR;
б) дисперсию D;
в) среднее квадратическое отклонение ;
г) коэффициент вариации V;
д) ошибку выборочного среднего.
4. Сделать вывод.
Исходные данные:
Число поднятий туловища
22 22 23 23 24 25 26 27 27 29 29 29
30 30 31 35

3.

1.Cоставим дискретный вариационный ряд
Все варианты расположим в порядке возрастания в первой строке
таблицы, а частоту, с которой они встречаются в данной выборке, во
второй строке.
Объем выборки n = 16
Исходные данные:
Число поднятий туловища
22 22 23 23 24 25 26 27 27 29 29 29
30 30 31 35
При расчете всех последующих характеристик используется округление
с точностью, соответствующей исходным значениям. Например, в
данном случае указаны целочисленные значения, поэтому все
результаты должны быть округлены с точностью до целых.

4.

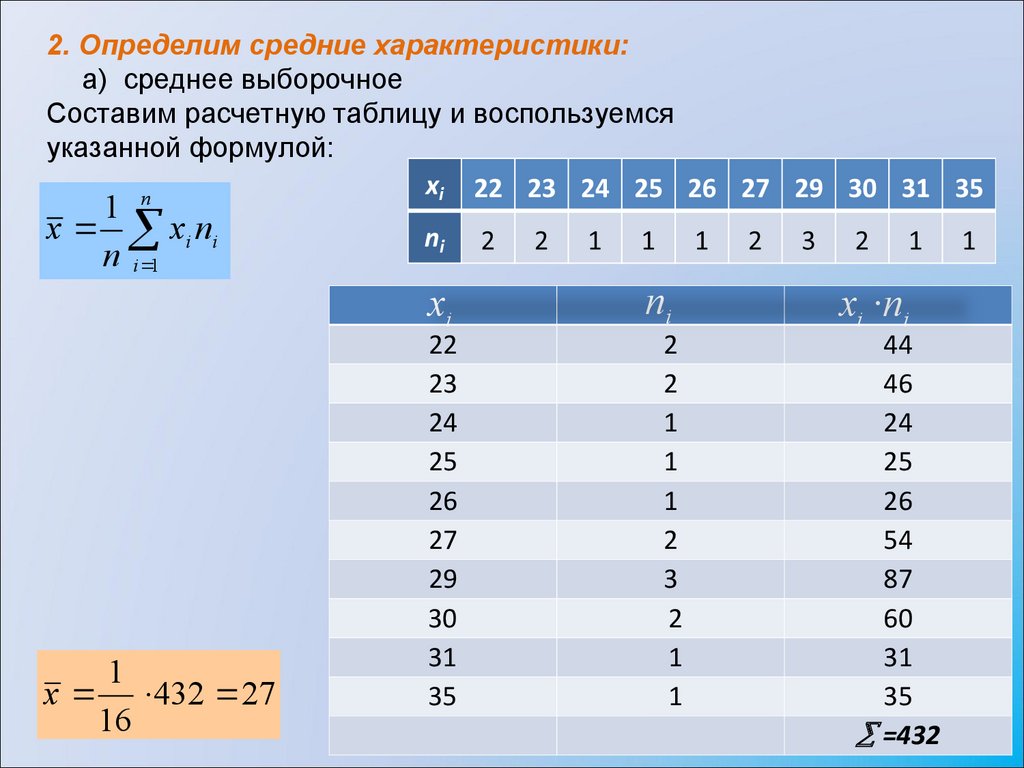
2. Определим средние характеристики:
а) среднее выборочное
Составим расчетную таблицу и воспользуемся
указанной формулой:
1 n
x x i ni
n i 1
xi
1
x 432 27
16
22
23
24
25
26
27
29
30
31
35
ni
2
2
1
1
1
2
3
2
1
1
xi ∙ni
44
46
24
25
26
54
87
60
31
35
=432

5.

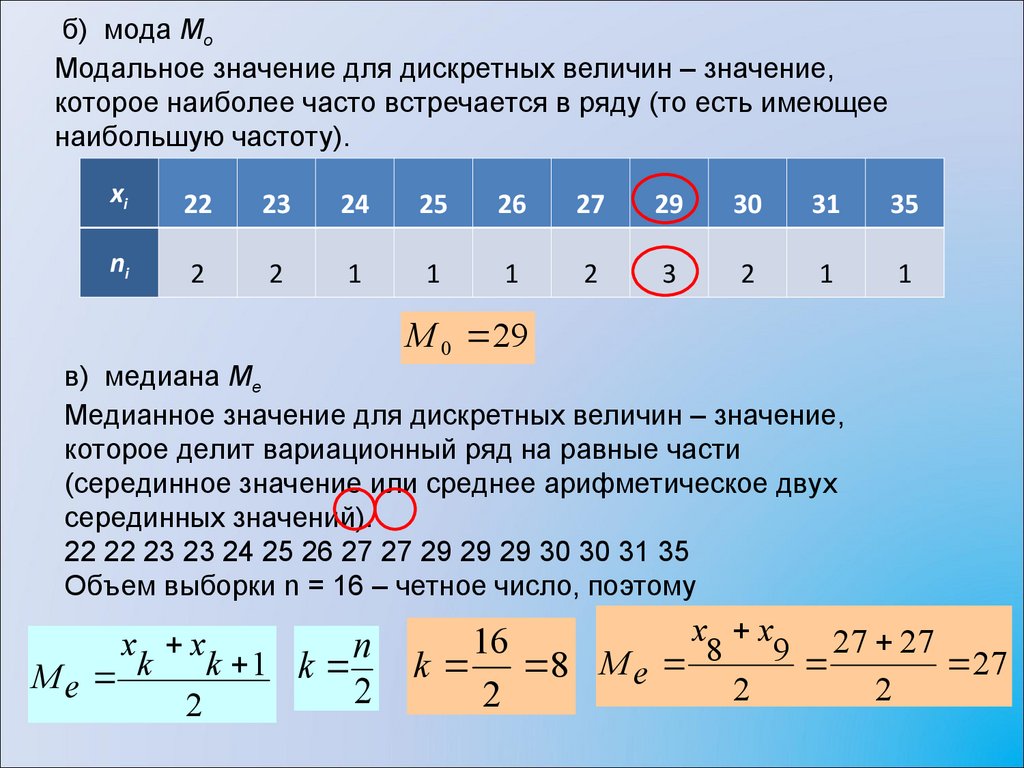
б) мода Mo
Модальное значение для дискретных величин – значение,
которое наиболее часто встречается в ряду (то есть имеющее
наибольшую частоту).
xi
22
23
24
25
26
27
29
30
31
35
ni
2
2
1
1
1
2
3
2
1
1
M 0 29
в) медиана Mе
Медианное значение для дискретных величин – значение,
которое делит вариационный ряд на равные части
(серединное значение или среднее арифметическое двух
серединных значений).
22 22 23 23 24 25 26 27 27 29 29 29 30 30 31 35
Объем выборки n = 16 – четное число, поэтому
x x
n
k
k
1
k
Me
2
2
x x
27 27
16
8
9
27
k 8 M e
2
2
2

6.

3. Определим характеристики вариации
а) размах вариации (разность между наибольшим и наименьшим
значениями):
X R xmax x
min
x
22
min
xmax 35
X R 35 22 13

7.

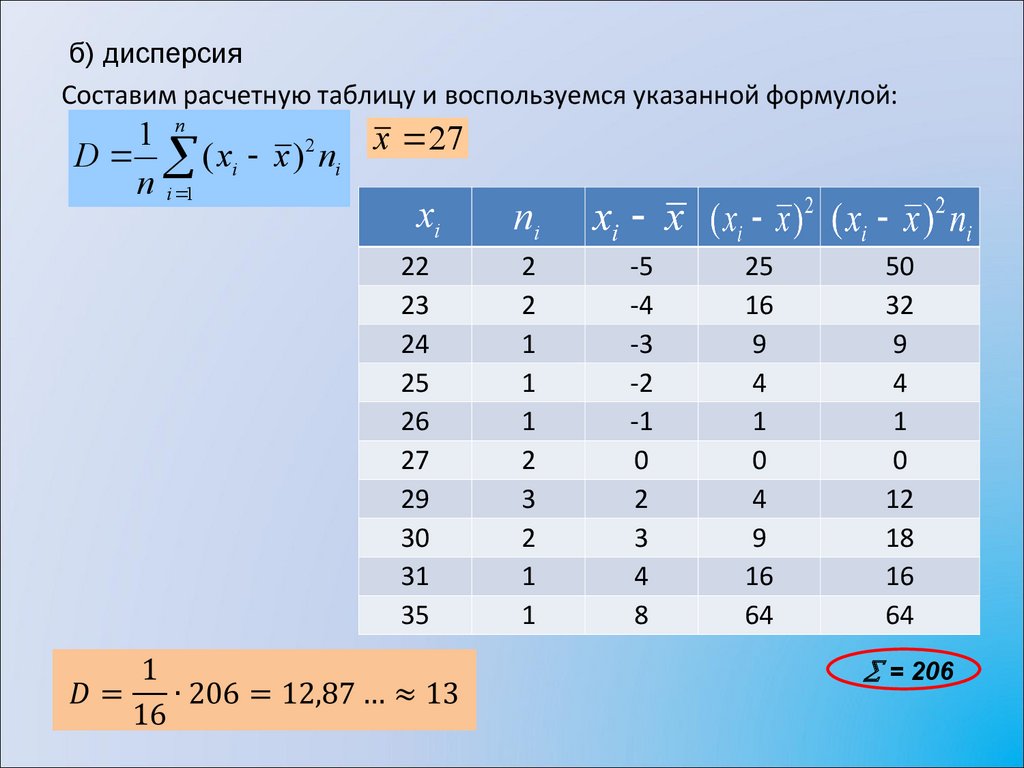
б) дисперсия
Составим расчетную таблицу и воспользуемся указанной формулой:
1 n
x 27
D ( xi x ) 2 ni
n i 1
xi
22
23
24
25
26
27
29
30
31
35
ni
2
2
1
1
1
2
3
2
1
1
-5
-4
-3
-2
-1
0
2
3
4
8
25
16
9
4
1
0
4
9
16
64
50
32
9
4
1
0
12
18
16
64
= 206

8.

в) среднее квадратическое отклонение:
D
г) коэффициент вариации:
V 100%
x
д) ошибка выборочного среднего: S x
n
x 27

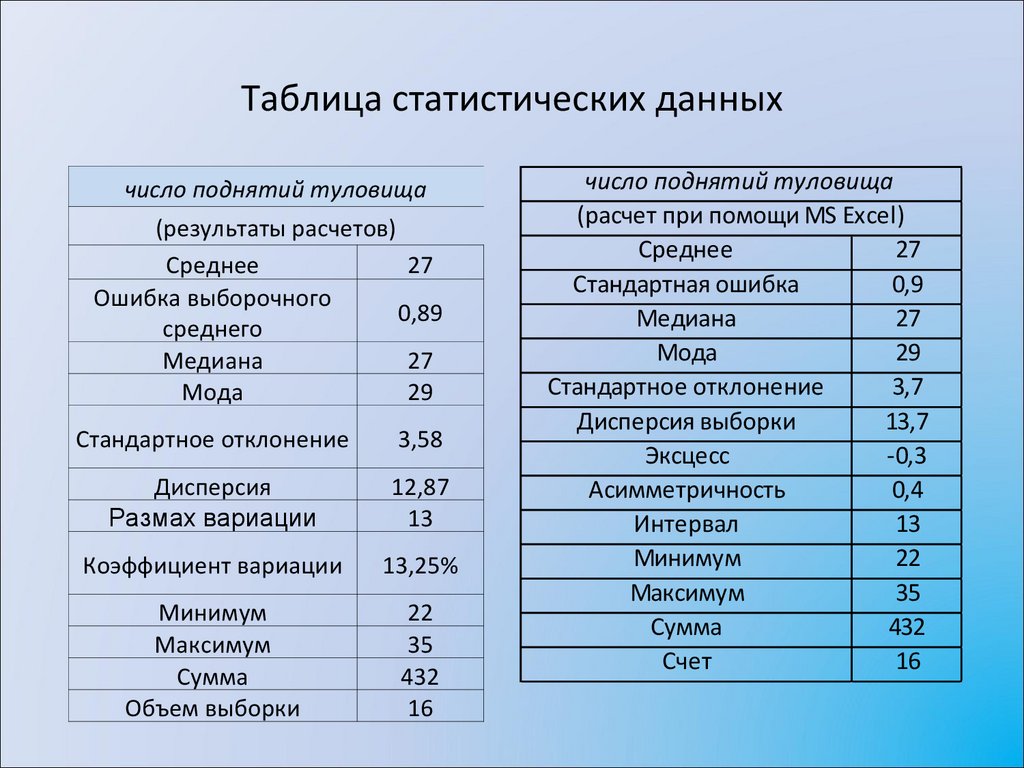
9. Таблица статистических данных

число поднятий туловища
(результаты расчетов)
Среднее
27
Ошибка выборочного
0,89
среднего
Медиана
27
Мода
29
Стандартное отклонение
3,58
Дисперсия
Размах вариации
12,87
13
Коэффициент вариации
13,25%
Минимум
Максимум
Сумма
Объем выборки
22
35
432
16
число поднятий туловища
(расчет при помощи MS Excel)
Среднее
27
Стандартная ошибка
0,9
Медиана
27
Мода
29
Стандартное отклонение
3,7
Дисперсия выборки
13,7
Эксцесс
-0,3
Асимметричность
0,4
Интервал
13
Минимум
22
Максимум
35
Сумма
432
Счет
16

10.

4. Вывод. По данным числа поднятий туловища у 16 испытуемых средний
результат составил 27 ± 1 раз. Среднее рассеяние данных выборки от
среднего результата составляет 4 поднятия туловища. Наиболее часто
встречаемый результат – 29 поднятий туловища. Половина спортсменов
показала результаты не хуже 27 поднятий туловища. Разница результатов
числа поднятий туловища внутри группы составила 13 раз. Результаты
исследования имеют малую варьируемость (13%), что подтверждает
однородность выборки, то есть средний результат типичен для
изучаемого признака.
M0
x S x M e
XR
V
n

11. НЕПРЕРЫВНЫЙ (ИНТЕРВАЛЬНЫЙ) ВАРИАЦИОННЫЙ РЯД

Задание: По данным выборки:
1. Составить интервальный вариационный ряд.
2. Построить гистограмму.
3. Найти средние характеристики:
а) среднее выборочное ;
б) моду Mo;
в) медиану Me.
4. Найти характеристики вариации:
а) размах вариации XR;
б) дисперсию D;
в) среднее квадратическое отклонение ;
г) коэффициент вариации V;
д) ошибку выборочного среднего.
Исходные
5. Сделать вывод.
данные:
Бег на 1000м ( 7 класс)
3,40 3,33 3,43 4,50 3,55 4,10 4,25 4,50
5,32 5,40 4,20 4,15 5,44 4,53 5,46 5,35

12.

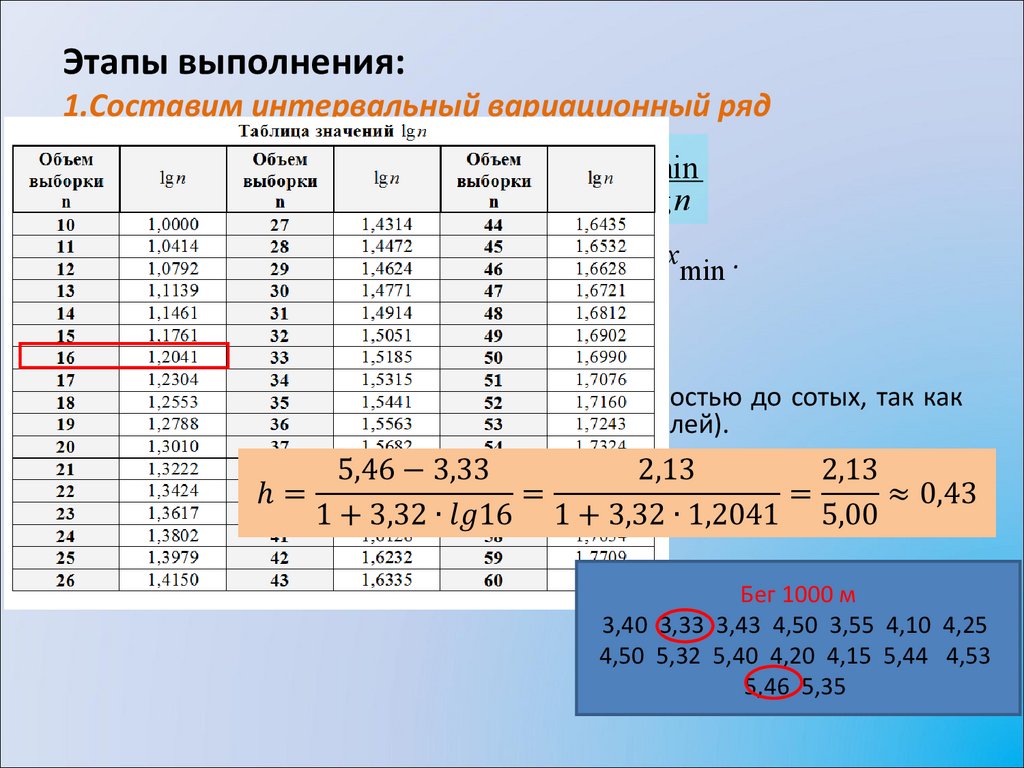
Этапы выполнения:
1.Cоставим интервальный вариационный ряд
xmax x
min
Определим величину интервала: h
1 3,32 lg n
Так как n=16, определим значения lg16, xmax и xmin .
lg16=1,2041, xmax 5,46 , xmin 3,33
(значение величины интервала округляем с точностью до сотых, так как
исходные данные имеют точность до сотых долей).
Бег 1000 м
3,40 3,33 3,43 4,50 3,55 4,10 4,25
4,50 5,32 5,40 4,20 4,15 5,44 4,53
5,46 5,35

13.

Найдем границы интервалов.
Левой границей первого интервала будет число
a1 x min
h
2
Вычисляем далее:
a 2 a1 h
a 3 a 2 h
x max 5,46

14.

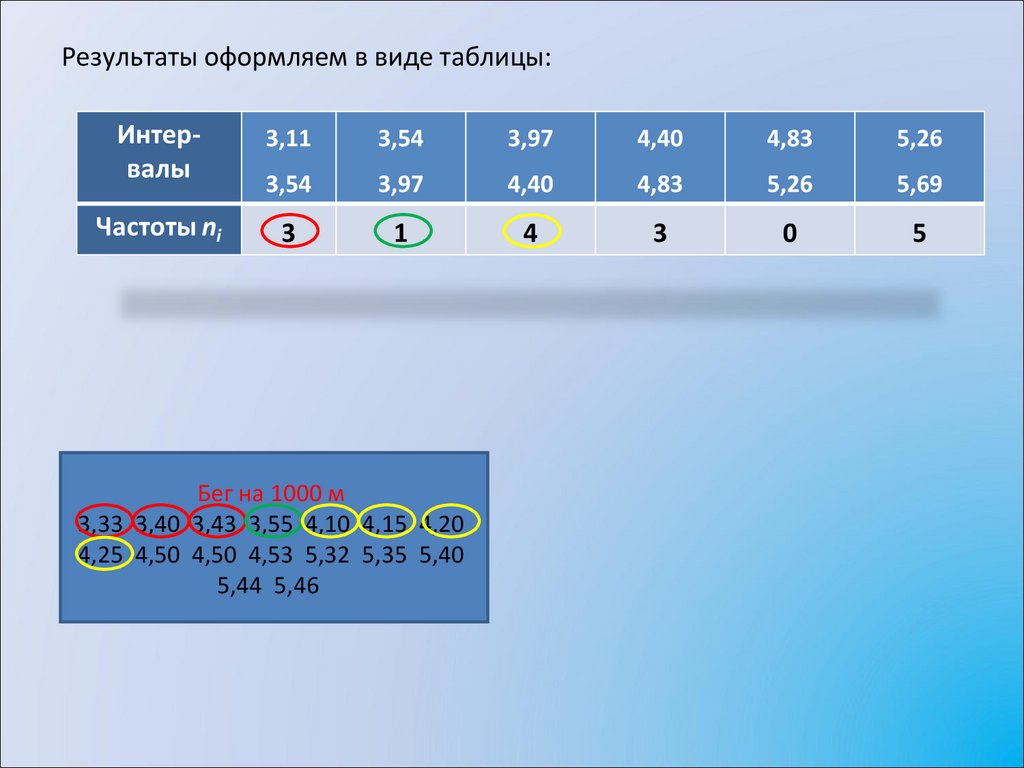
Результаты оформляем в виде таблицы:
Бег на 1000 м
3,33 3,40 3,43 3,55 4,10 4,15 4,20
4,25 4,50 4,50 4,53 5,32 5,35 5,40
5,44 5,46

15.

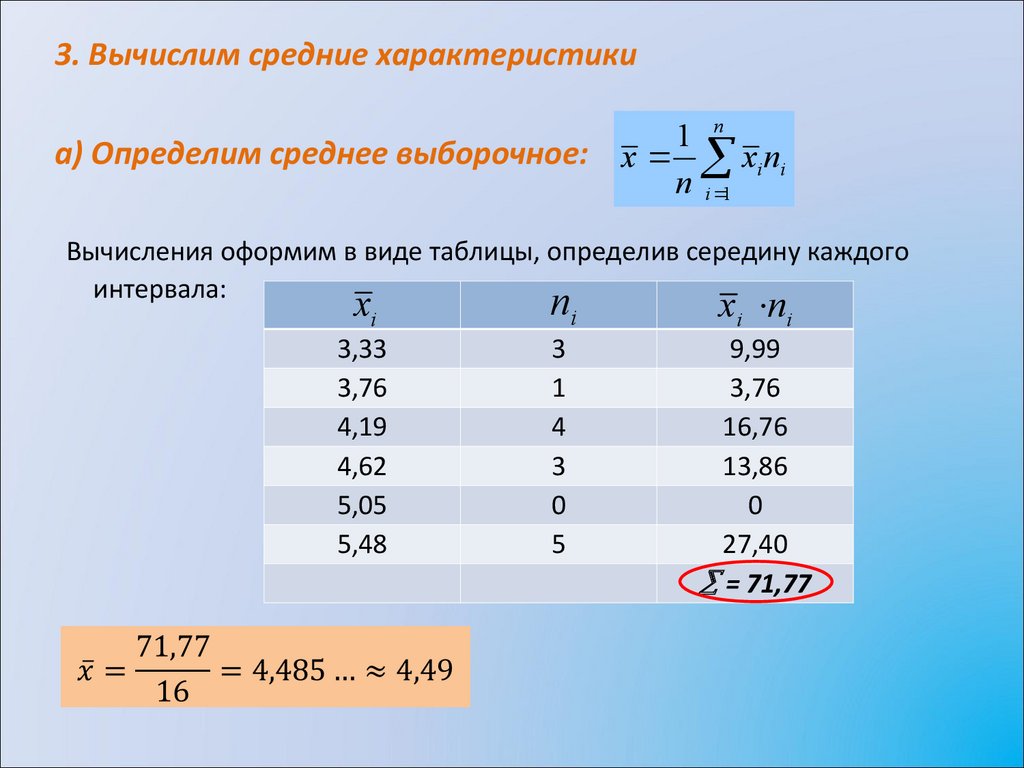
3. Вычислим средние характеристики
1 n
а) Определим среднее выборочное: x xi ni
n i 1
Вычисления оформим в виде таблицы, определив середину каждого
интервала:
xi
ni
xi ni
3,33
3,76
4,19
4,62
5,05
5,48
3
1
4
3
0
5
9,99
3,76
16,76
13,86
0
27,40
= 71,77

16.

б) определим моду:
M 0 a1M 0 h
nM 0 nM 0 1
2n M 0 n M 0 1 n M 0 1

17.

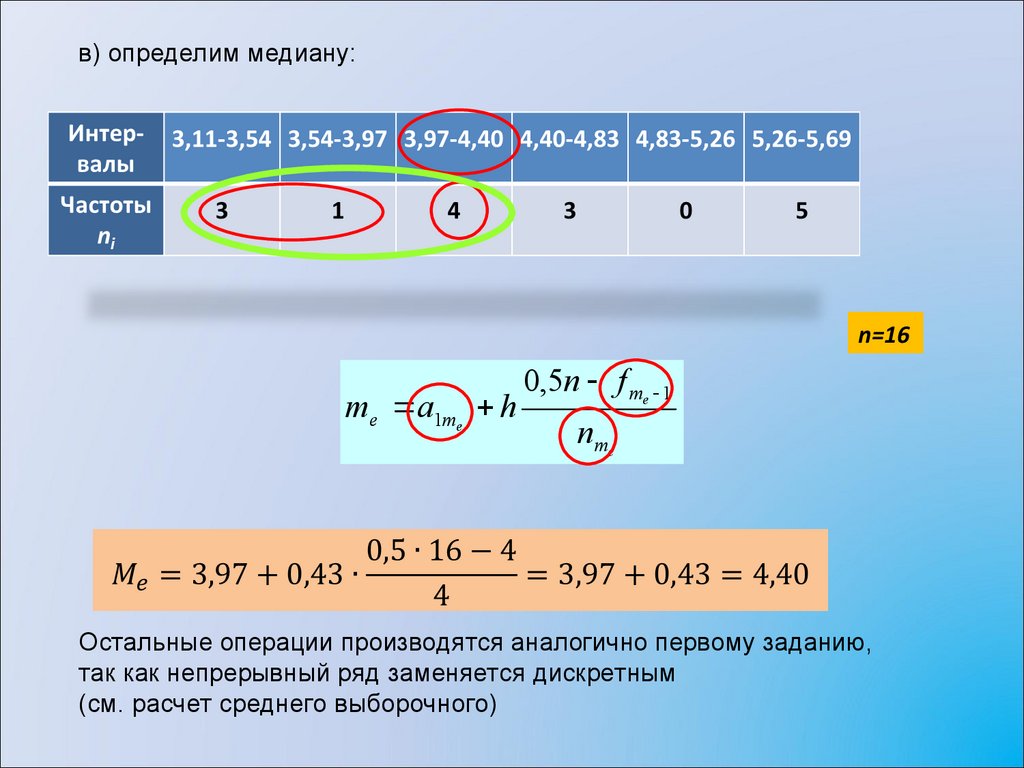
в) определим медиану:
n=16
me a1me h
0,5n f me 1
n me
Остальные операции производятся аналогично первому заданию,
так как непрерывный ряд заменяется дискретным
(см. расчет среднего выборочного)