Основы теории напряженного и деформированного состояний (продолжение)

1.

ОСНОВЫ ТЕОРИИ
НАПРЯЖЕННОГО И
ДЕФОРМИРОВАННОГО
СОСТОЯНИЙ
(продолжение)

2.

Закон Гука. Упругие характеристики
изотропного тела
Деформации материала конструкции в каждой точке
прямо пропорциональны напряжениям в этой точке:
σ =Еε,
G
Модуль продольной упругости Е (модуль Юнга) характеризует
способность материала сопротивляться растяжению.
Модуль сдвига G определяет способность материала
сопротивляться изменению формы при сохранении его объёма.

3.

Коэффициент Пуассона μ
попер
прод
G
E
;
2 1
Обобщенный закон Гука для изотропного материала
1
y
z
x E x
1
y x z
y
E
1
z E z y x
xy
yz
xy ; yz ; xz xz
G
G
G

4.

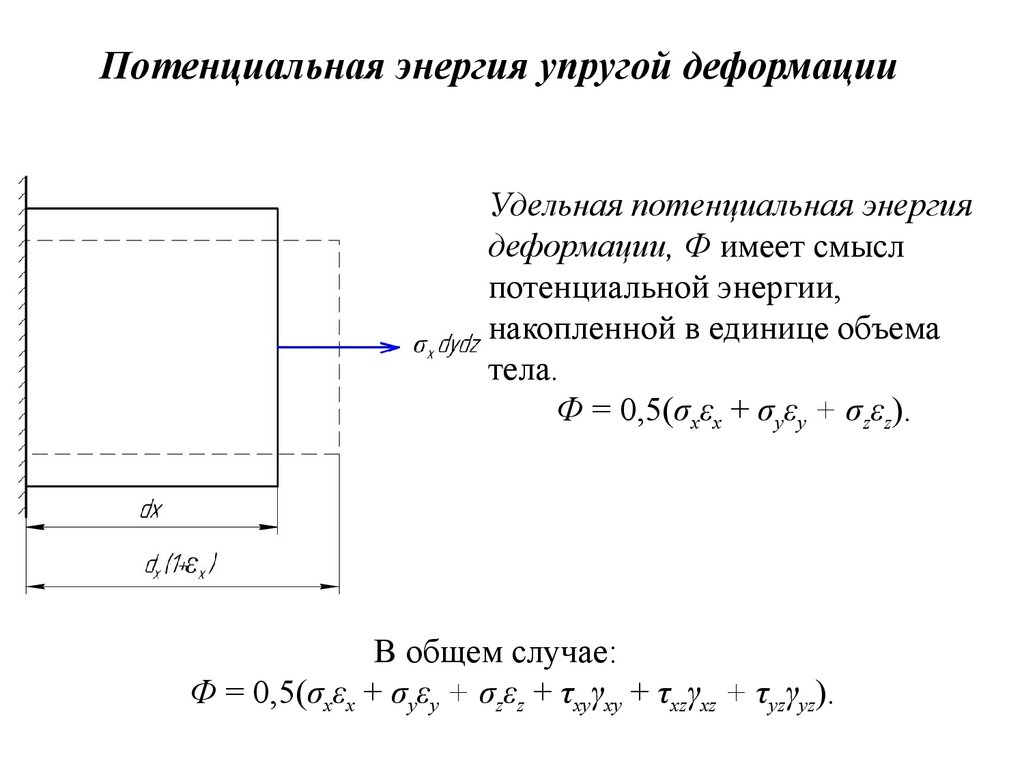
Потенциальная энергия упругой деформации
Удельная потенциальная энергия
деформации, Ф имеет смысл
потенциальной энергии,
накопленной в единице объема
тела.
Ф = 0,5(σхεх + σyεy + σzεz).
В общем случае:
Ф = 0,5(σхεх + σyεy + σzεz + τхуγху + τхzγхz + τyzγyz).

5.

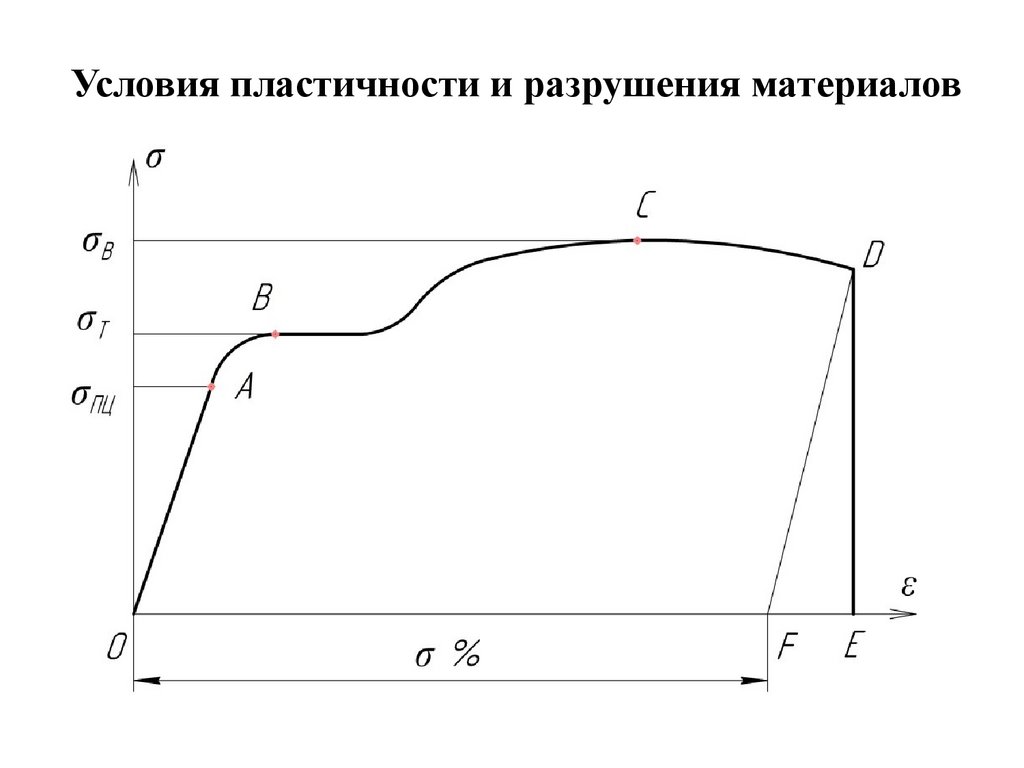
Условия пластичности и разрушения материалов

6.

Наибольшее напряжение, при котором сохраняется
пропорциональная зависимость между
напряжениями и деформациями называется
пределом пропорциональности σпц .
Напряжение, при котором начинает развиваться
пластическая деформация, называется
пределом текучести σТ
Напряжение, выше которого происходит разрушение
материала, называется пределом прочности σв.

7.

Предельные условия перехода
в пластическое состояние и разрушение
При одноосном растяжении
Условие прочности
σ1 = σТ; σ1 = σв
σ1max ≤ [σ]
Если для любого сложного напряжённого состояния можно найти ему
равноопасное одноосное напряжённое состояние, осуществляемое
некоторым эквивалентным напряжением σэкв = f (σ1, σ2, σ3),
являющимся комбинацией главных напряжений, то
предельные условия при сложном напряжённом состоянии
σэкв = σТ; σэкв = σв,
условие прочности
σЭКВmax ≤ [σ].

8.

Условие пластичности Сен-Венана: свойство пластичности
материала при сложном напряжённом состоянии начинает
проявляться тогда, когда максимальное касательное напряжение
достигает некоторого предельного постоянного значения:
max 1 3 k ,
2
условие прочности: σэкв = σ1 - σ3 ≤ [σ].
Условие
пластичности Мизеса:
материал переходит в
пластическое
состояние
тогда,
когда
октаэдрическое
касательное напряжение достигает некоторого предельного
постоянного значения:
1
окт 1 2 2 2 3 2 3 1 2 max k ,
3
1
экв
1 2 2 2 3 2 3 1 2 Т
2

9.

Теории прочности
Если в материале происходит качественное изменение свойств переход от одного механического состояния к другому,
наступает предельное или опасное напряженное состояние.
При расчете на прочность ориентируются на так называемое
допускаемое состояние, которое соответствует нагрузке,
полученной путем деления предельной нагрузки, на некоторый
коэффициент запаса прочности.
Если в двух напряженных состояниях коэффициенты запаса
равны, то они называются равноопасными.
Эквивалентное напряжение σэкв - это такое напряжение,
которое следует создать в растянутом образце, чтобы его
напряженное состояние было равноопасно заданному
напряженному состоянию.

10.

Первая теория прочности — теория наибольших
нормальных напряжений.
В первой теории прочности. за критерий перехода
материала в предельное состояние принимается наибольшее
нормальное напряжение.
Условие прочности имеет вид:
I
экв
I
где экв 1 , если
1 3

11.

Вторая теория прочности - теория наибольших
относительных удлинений
,
Во второй теории прочности за критерий
перехода
,
материала в предельное состояние
принимается наибольшая деформация.
Условие прочности для пластичного материала:
где
E
,
max
для
хрупкого
материала:
c
min c
E
p
max p
E

12.

Третья теория прочности — теория наибольших
касательных напряжении
В третьей теории прочности за критерий перехода материала
в
предельное
состояние
принимается
наибольшее
.
касательное напряжение.
Условие прочности имеет
вид:
1 3
max
,
2
.
где
2

13.

.
Четвертая теория прочности — энергетическая.
Критерий перехода материала в предельное состояние удельная потенциальная энергия изменения формы
Условие
прочности:
Ф Ф
гд
е
1
Ф
3Е

14.

Теория прочности Мора
(теория предельных напряженных состояний)
аналитическое выражение условия прочности:
р
1 3
р
с

15.

Условия прочности по допускаемым
.
напряжениям
Предел текучести для пластичного
материала:
Т р Т с Т
Предел прочности для хрупкого материала:
.
с
в в р
σТmax < σпред.
Расчетный коэффициент запаса
прочности:
пред
n
1
Т max
пред
n
n
Условие
Т max
прочности:
Допускаемое напряжение: пред
n