Исследование напряженно-деформированного состояния в точке тела. Лекция 6

1. Тема Исследование напряженно-деформированного состояния в точке тела

2. Теории предельного состояния материала в локальной области

Основная задача: оценка прочности
по известному напряженному состоянию.
При линейном напряженном состоянии →
значение опасных напряжений легко установить
экспериментально
(испытания образцов на простое растяжение или сжатие).
•Опасное напряжение - ? соответствующее
– при хрупком состоянии материала;
началу разрушения
– при пластичном состоянии материала.
появлению остаточных деформаций
оп в
оп Т

3. Теории предельного состояния материала в локальной области

• Наиболее просто → при линейном напряженном состоянии → значение
опасных напряжений легко установить экспериментально (испытания
образцов на простое растяжение или сжатие).
• Под опасным напряжением понимают напряжения, соответствующие
началу разрушения
–
– при хрупком состоянии материала;
оп
пч
появлению остаточных деформаций
–
– при пластичном состоянии материала.
оп
Т
Прочность материала при сложном напряженном состоянии:
оп пч
оп пч

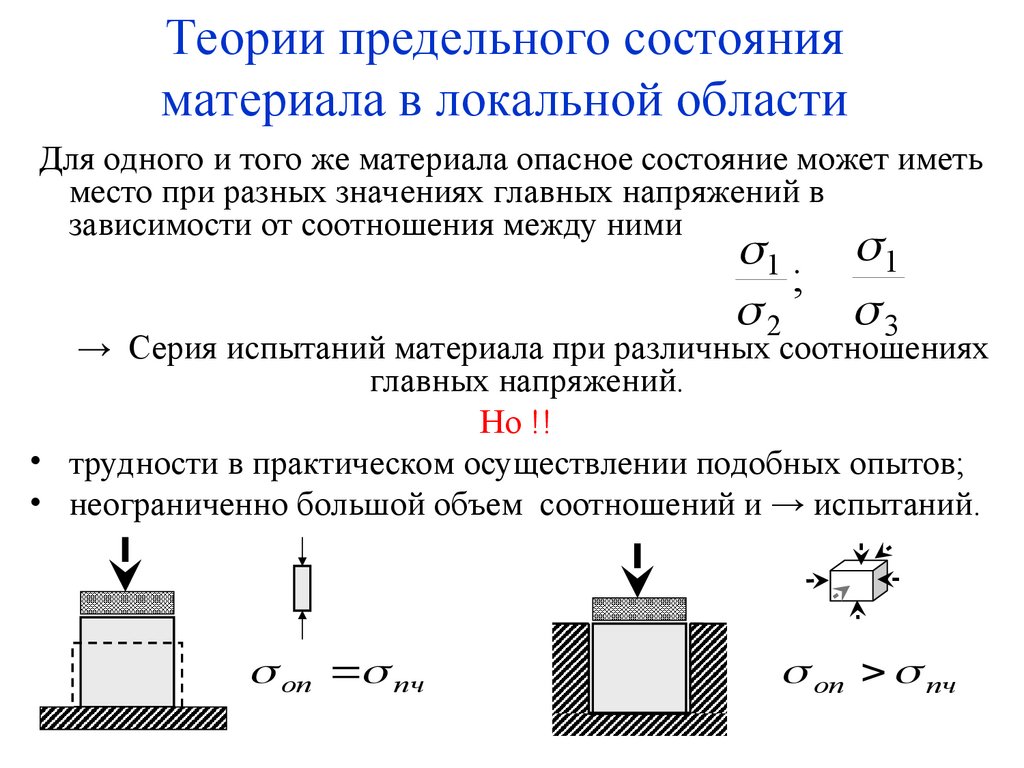
4. Теории предельного состояния материала в локальной области

Для одного и того же материала опасное состояние может иметь
место при разных значениях главных напряжений в
зависимости от соотношения между ними
1
;
2
1
3
→ Серия испытаний материала при различных соотношениях
главных напряжений.
Но !!
• трудности в практическом осуществлении подобных опытов;
• неограниченно большой объем соотношений и → испытаний.
оп пч
оп пч

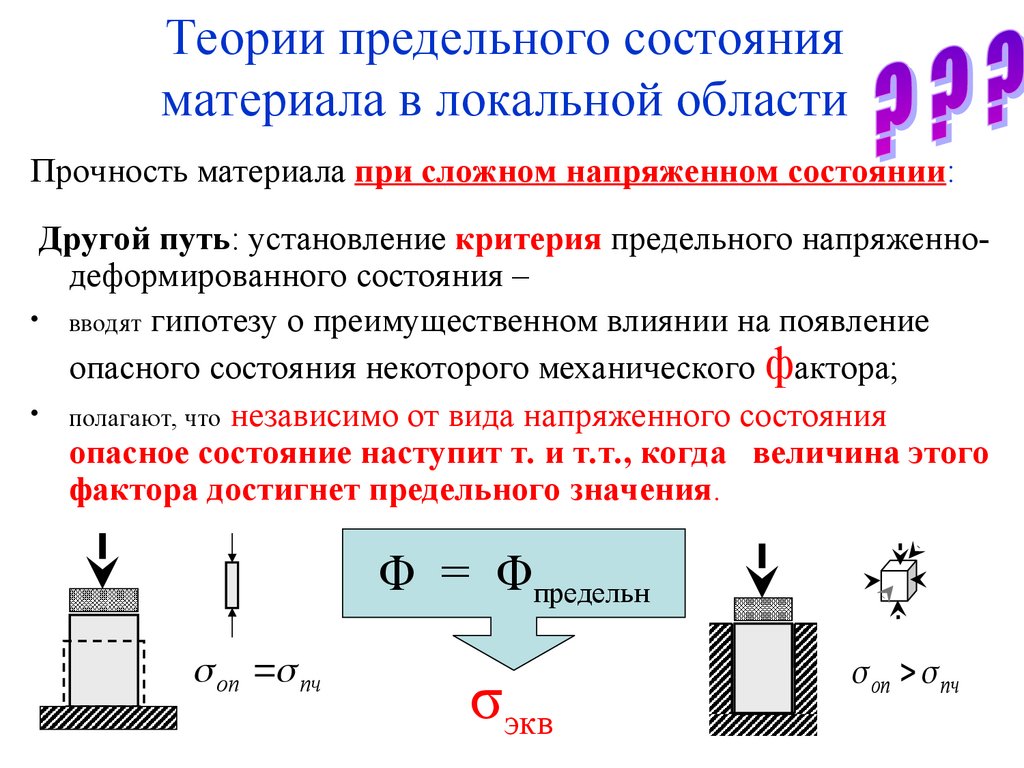
5. Теории предельного состояния материала в локальной области

Прочность материала при сложном напряженном состоянии:
Другой путь: установление критерия предельного напряженнодеформированного состояния –
• вводят гипотезу о преимущественном влиянии на появление
опасного состояния некоторого механического фактора;
• полагают, что независимо от вида напряженного состояния
опасное состояние наступит т. и т.т., когда величина этого
фактора достигнет предельного значения.
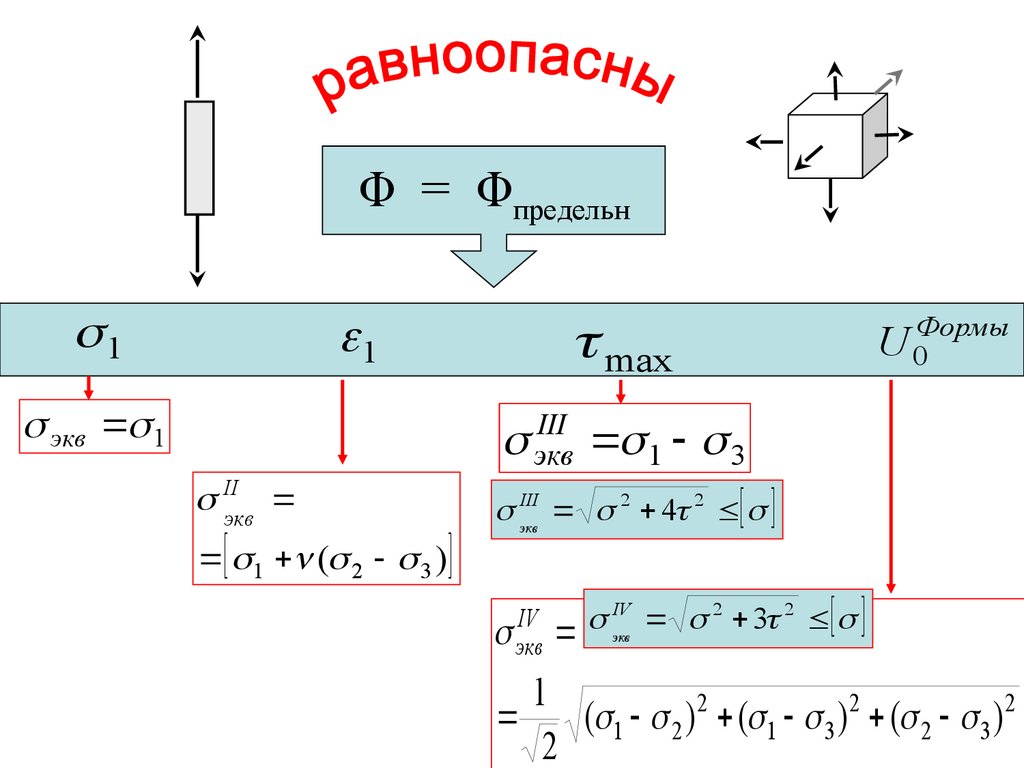
Φ = Φпредельн
оп пч
σэкв
оп пч

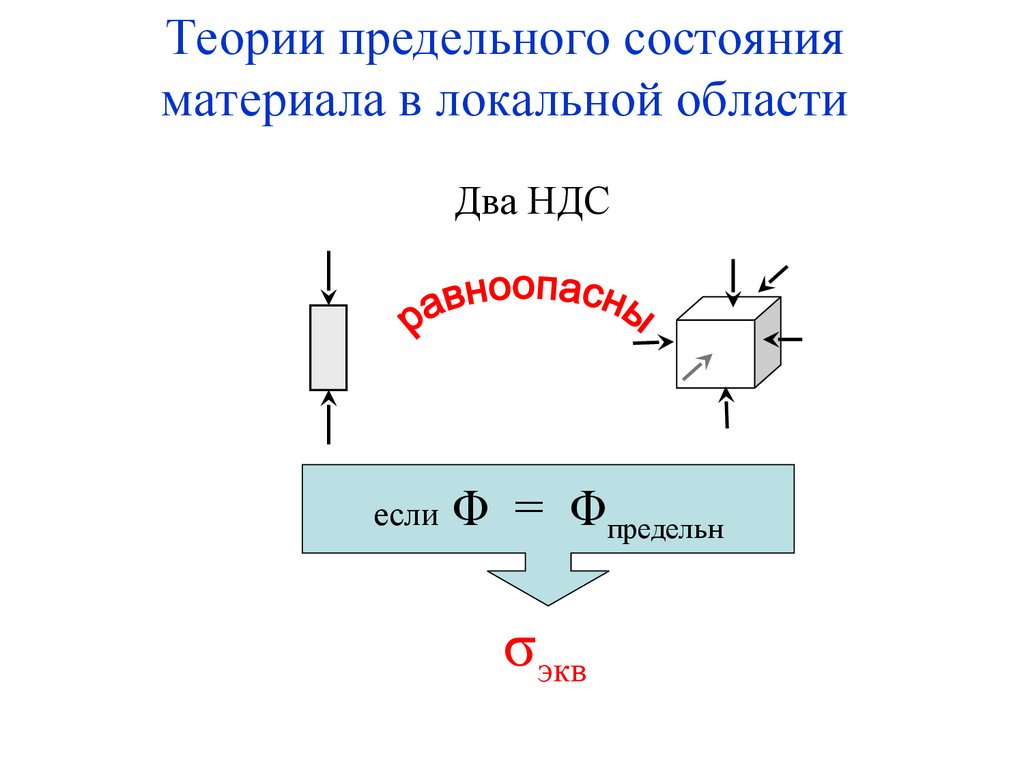
6. Теории предельного состояния материала в локальной области

Два НДС
если
Φ = Φпредельн
σэкв

7. Первая теория прочности

Ф = σ1
• Причина наступления предельного состояния

достижение наибольшим нормальным напряжением
предельной величины.
• Условие
наступления
Независимо
от вида напряженного
эквсостояния
1 оп
предельного
опасноесостояния:
состояние наступит т. и т.т., когда
величина этого фактора достигнет предельного
• Условие прочности значения.
экв 1
• В случае сжатия
то же условие сохраняется,
но
экв 3

8. Первая теория прочности

Ф = σ1
• Два главных напряжения не участвуют в оценке
прочности.
• Тогда как, например,
• при всестороннем сжатие материалы не обнаруживают
признаков разрушения даже при напряжениях,
превышающих предел прочности при сжатии.
.
• Дает (редко)
удовлетворительные результаты
для весьма хрупких материалов
(кирпич, керамика)
экв 1
экв 3

9. Вторая теория прочности – критерий наибольших линейных деформаций

Вторая теория прочности –
Ф=
критерий наибольших линейных деформаций
Условие наступления предельного состояния
предельное значение
наибольшей относительной деформации
ε1
экв 1 оп
Условие прочности
экв оп
Независимо от вида напряженного kсостояния
опасное состояние наступит
т. и т.т., когда
.
• При линейном НС
достигнет предельного
величина этого фактора
E
значения.
1
• В общем случае НС
1 1 ( 2 3 )
• Таким образом
E
1
( )
E
1
экв
2
E
3
( )
1
2
3

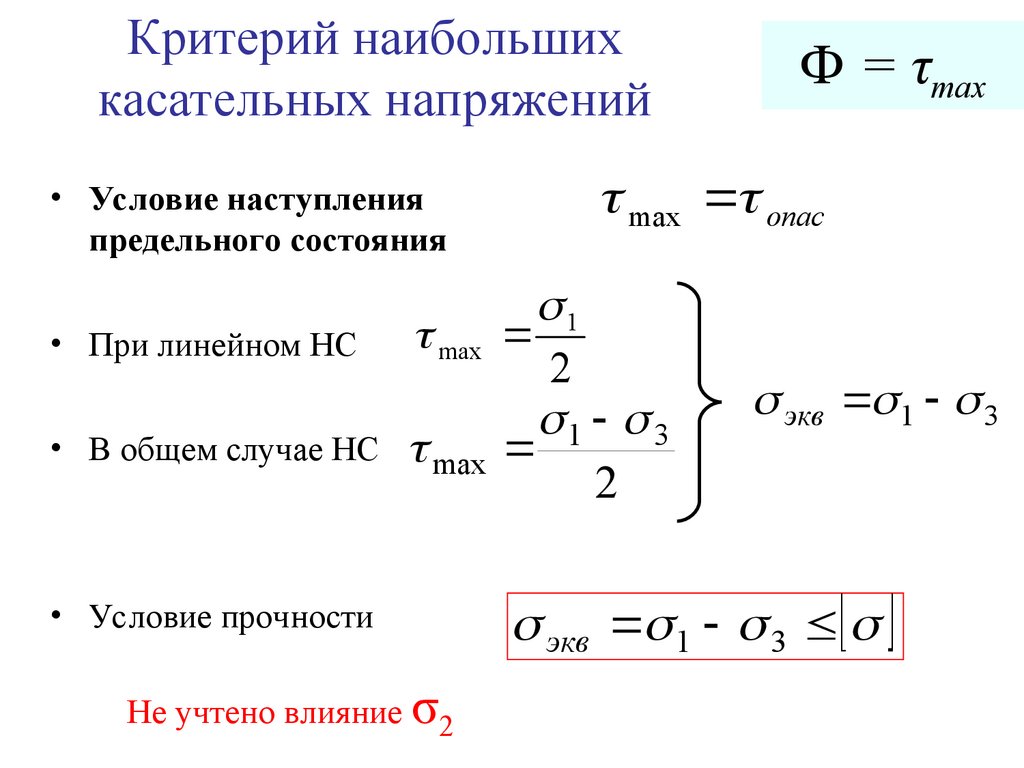
10. Критерий наибольших касательных напряжений

Ф = τmax
пластичности
• ( условно – «Третья теория прочности»)
• Предельное состояние наступает тогда, когда опасного
значения достигает наибольшее касательное напряжение.
Независимо от вида напряженного состояния
опасное
состояние наступит т. и т.т., когда
Условие
наступления
величина состояния
этого фактора достигнет
max предельного
опас
предельного
значения.
Появление массовых пластических деформаций
связывают со скольжением слоев атомов по
некоторым плоскостям, это становится возможным,
когда касательные напряжения достигают
предельной величины.

11. Критерий наибольших касательных напряжений

max опас
• Условие наступления
предельного состояния
• При линейном НС
• В общем случае НС
max
max
• Условие прочности
Не учтено влияние σ2
Ф = τmax
1
2
1 3
2
экв 1 3
экв 1 3

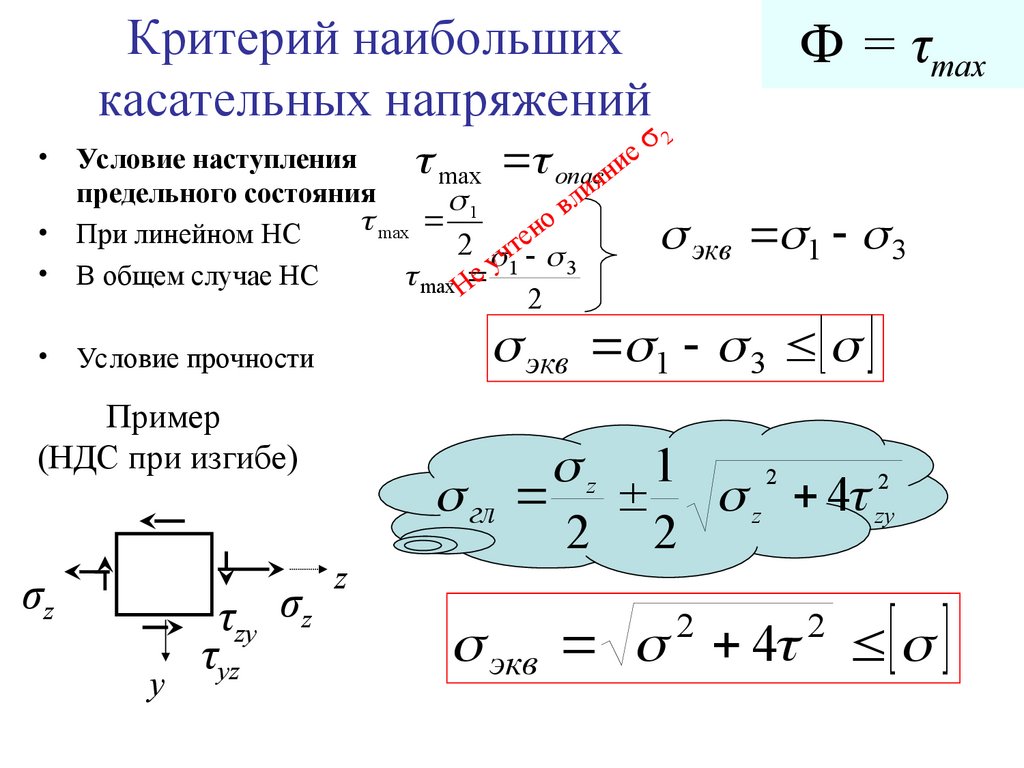
12. Критерий наибольших касательных напряжений

Ф = τmax
σ
е
• Условие наступления
max опасяни
предельного состояния
ли
1
в
max
но
• При линейном НС
е
2 чт
3
• В общем случае НС
max Н е у 1
2
2
экв 1 3
экв 1 3
• Условие прочности
Пример
(НДС при изгибе)
σz
τzy σz
y
τyz
z
z 1
2
2
гл z 4 zy
2 2
2
2
экв 4

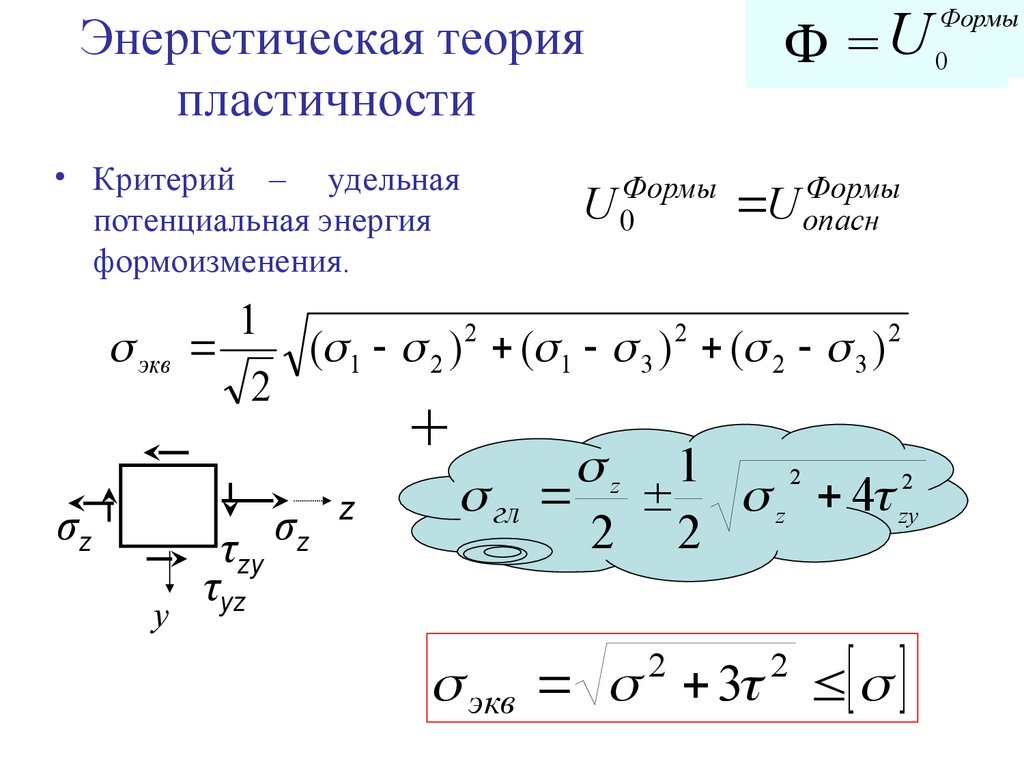
13. Энергетическая теория пластичности

Ф =U
τmax
0
Формы
Энергетическая теория
пластичности
• Критерий – удельная потенциальная энергия
формоизменения.
Формы
U0
Формы
U опасн
• В общем
случае НСот вида напряженного состояния
Независимо
U
Формы
0
опасное состояние наступит т. и т.т., когда
1
об
2
2
величина
этого
фактора
достигнет
предельного
U 0 U 0
[( 1 2 ) ( 1 3 ) ( 2
6E
значения.
• При линейном НС
экв
1
2
U
2
Формы
0
U 0 U
2
об
0
2
3) ]
1 2
3E
( 1 2 ) ( 1 3 ) ( 2 3 )
2

14. Энергетическая теория пластичности

Ф =U
τmax
0
Формы
Энергетическая теория
пластичности
• Критерий – удельная
потенциальная энергия
формоизменения.
экв
σz
1
2
σ
τzy z
y
Формы
U0
Формы
U опасн
( 1 2 ) 2 ( 1 3 ) 2 ( 2 3 ) 2
+
z
z 1
2
2
гл z 4 zy
2 2
τyz
2
2
экв 3

15.

Φ = Φпредельн
1
1
max
U 0Формы
III
экв
1 3
экв 1
IIэкв
III
экв
2 4 2
1 ( 2 3 )
IV
экв
IV
2
2
3
экв
1
( 1 2 ) 2 ( 1 3 ) 2 ( 2 3 ) 2
2