Напряженно-деформированное состояние в точке

1.

ОСНОВЫ ТЕОРИИ
НАПРЯЖЕННОГО
СОСТОЯНИЯ
Напряженнодеформированное состояние
в точке

2.

Напряжения являются результатом взаимодействия
частиц тела при его нагружении.
Внешние силы стремятся изменить взаимное
расположение частиц,
а возникающие при этом напряжения препятствуют
их смещению.
Расположенная в данной точке частица по- разному
взаимодействует с каждой из соседних частиц.
Поэтому в общем случае в одной и той же точке
напряжения различны по различным направлениям

3.

Напряженное
состояние в точке
тела задано,
если известны
напряжения
на любых трех
проходящих через
нее взаимно
перпендикулярных
площадках

4. Главные напряжения:

нормальные напряжения,
которые действуют по граням
элементарного параллелепипеда,
вырезанного в окрестностях
исследуемой точки,
при условии, что
касательные напряжения
на этих гранях
отсутствуют

5.

Главные напряжения обозначают
1, 2 , 3.
При этом
1 2 3

6.

Классификация
видов
напряженного состояния

7.

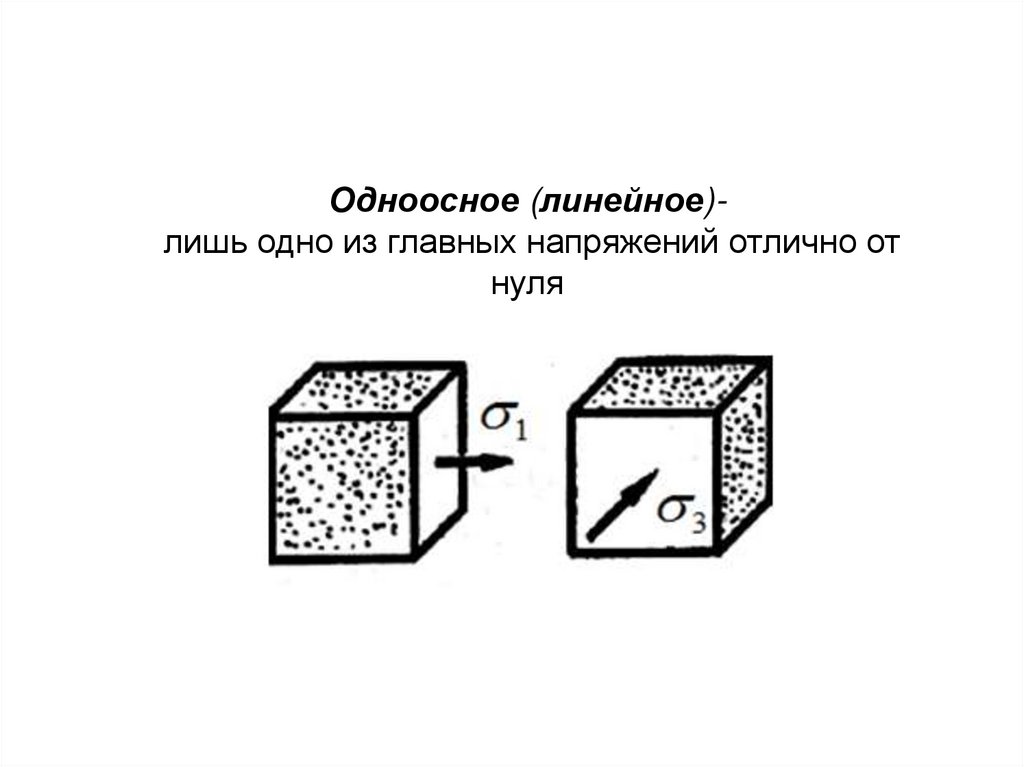
Одноосное (линейное)лишь одно из главных напряжений отлично от
нуля

8.

Плоское (двухосное) –
одно из главных напряжений
равно нулю

9.

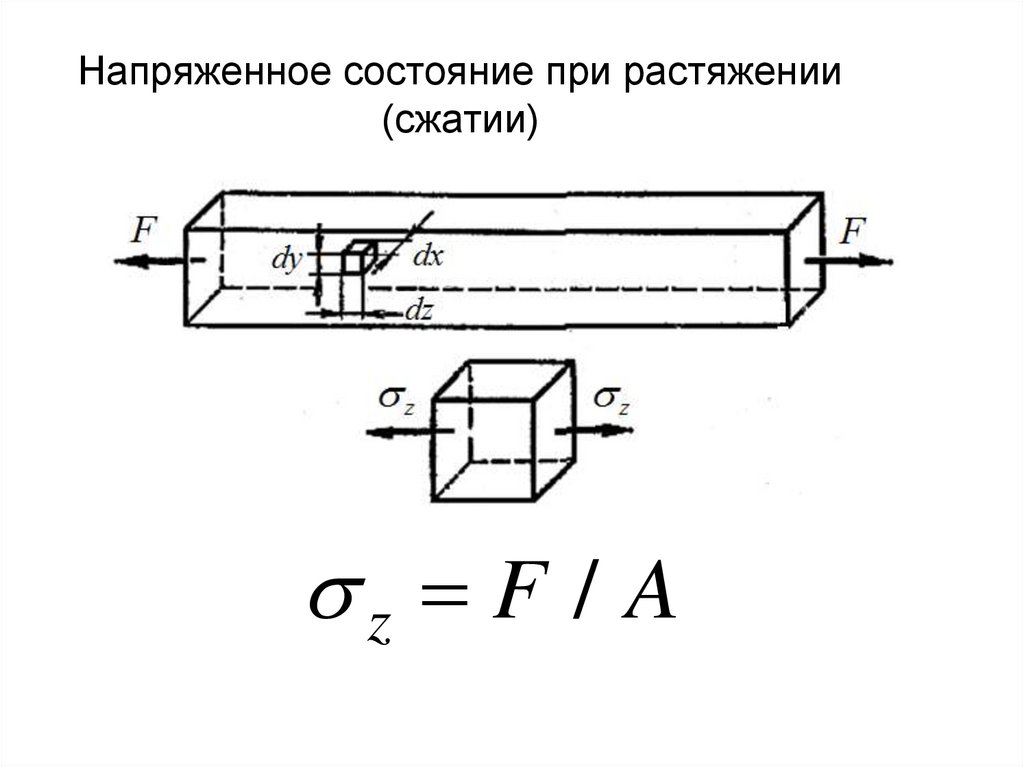
Объемное (трехосное)все три главных напряжения отличны от нуля

10. Напряженное состояние при растяжении (сжатии)

z F / A

11.

12.

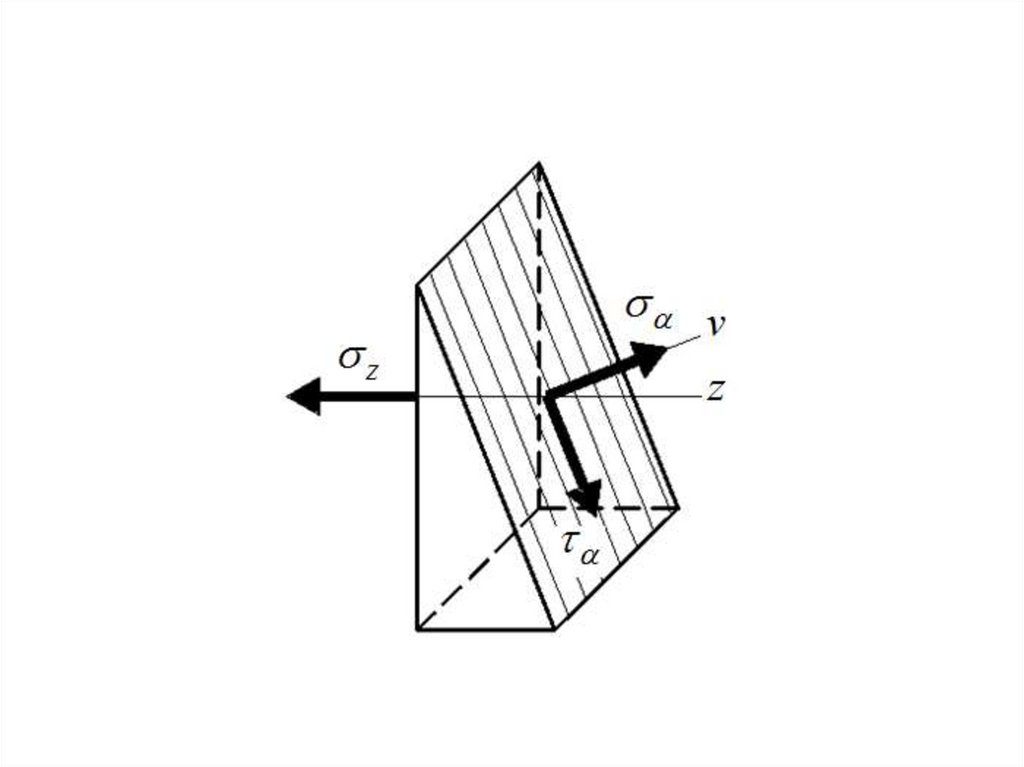
13. Уравнения равновесия составляются для сил, а не для напряжений, т. е. каждое из напряжений следует умножить на площадь грани,

на которой оно возникает

14.

Pi 0;
z (dA cos )cos dA 0;
z cos ; (a)
2

15.

Pit 0;
z dA cos sin dA 0;
1
z cos sin или z sin 2 (b)
2

16. Некоторые выводы из полученных результатов

Наибольшее нормальное
напряжение возникает
в поперечном сечении бруса:
max 0o z F / A

17.

Наибольшее касательное напряжение возникает
на площадке,
наклоненной под углом 45° к оси бруса,
и равно половине нормального напряжения,
возникающего в соответствующей точке
поперечного сечения:
max 45o z / 2

18.

Из формулы
1
z sin 2
2
вытекает равенство (по абсолютному значению) касательных
напряжений, возникающих на взаимно перпендикулярных площадках:
90
1
o
z sin 2( 90 )
2
1
o
z sin(2 180 )
2
1
z sin 2
2

19.

Это равенство носит название
закона парности
касательных напряжений

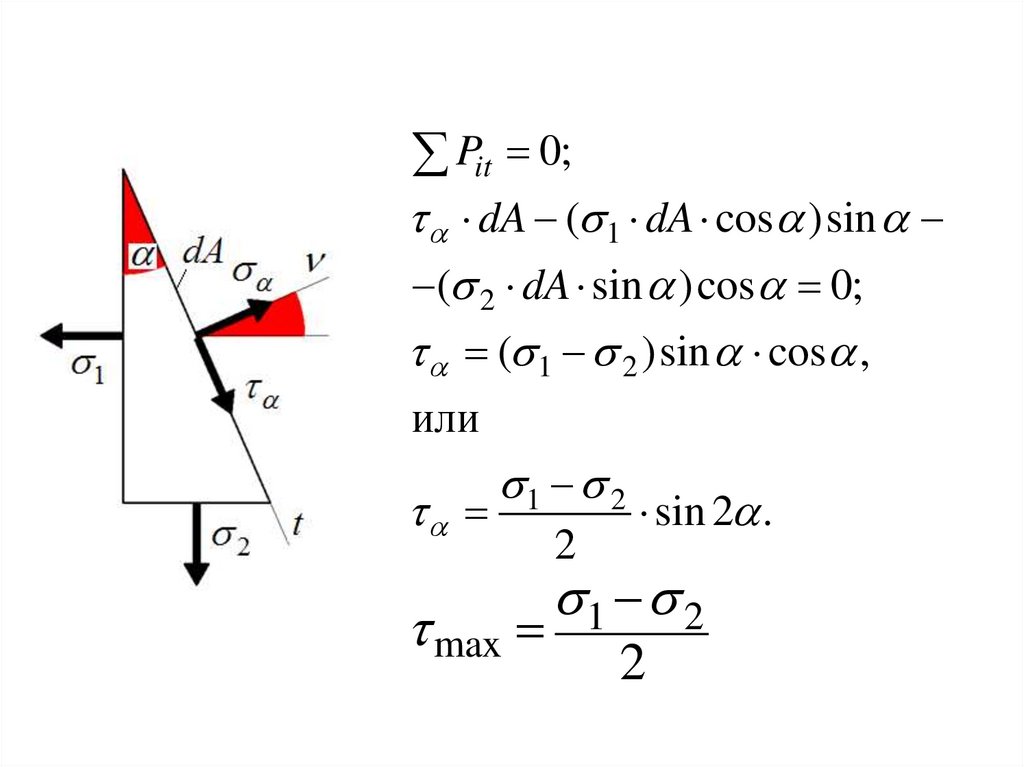
20. Исследование напряженного состояния при известных главных напряжениях

Pi 0;
dA ( 1 dA cos )cos
( 2 dA sin )sin 0;
1 cos 2 sin
2
2

21.

Pit 0;
dA ( 1 dA cos )sin
( 2 dA sin )cos 0;
( 1 2 )sin cos ,
или
1 2
max
2
sin 2 .
1 2
2

22.

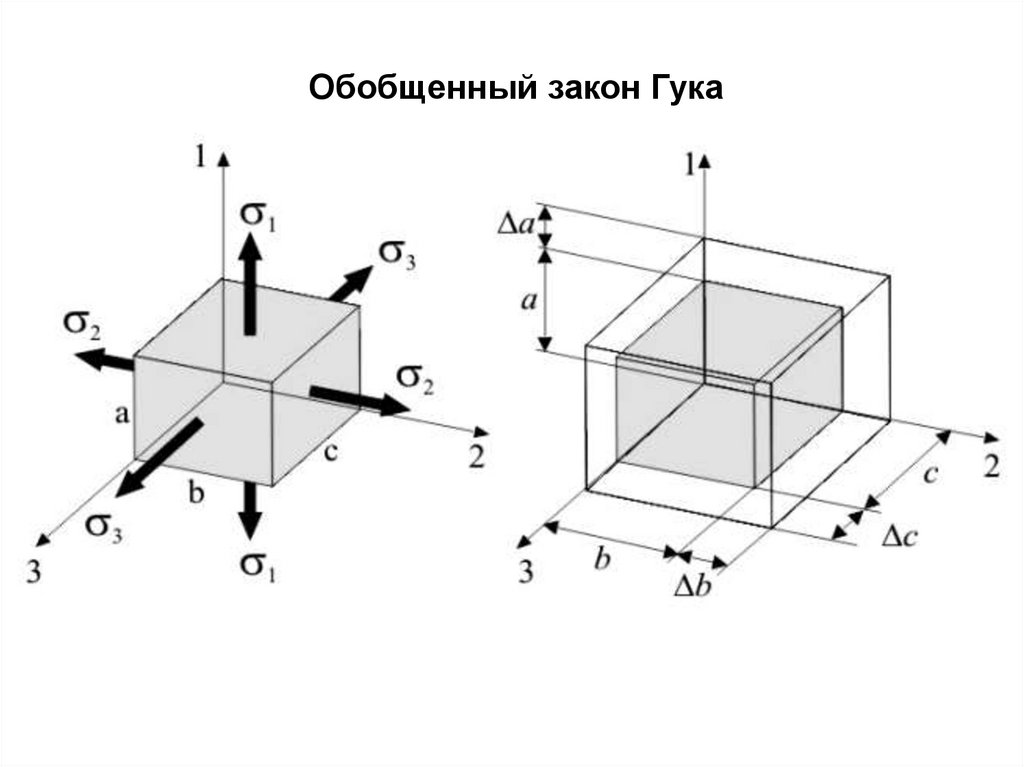
Обобщенный закон Гука

23.

24.

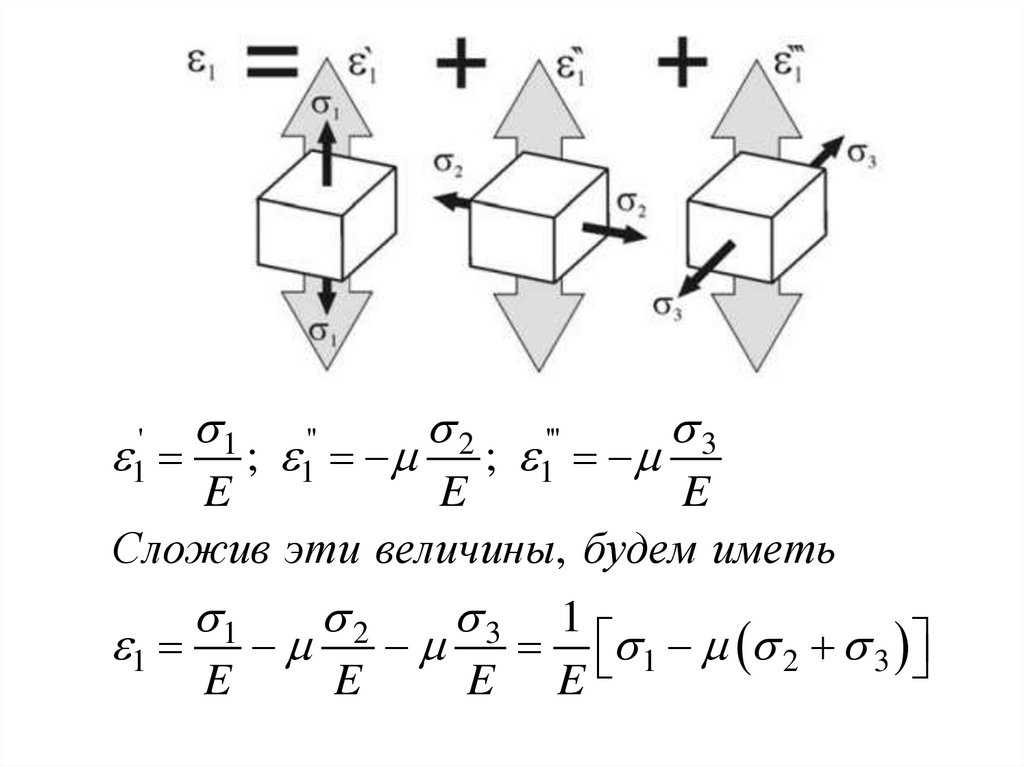
Применяя принцип суперпозиции
'
1 1
''
1
'''
1

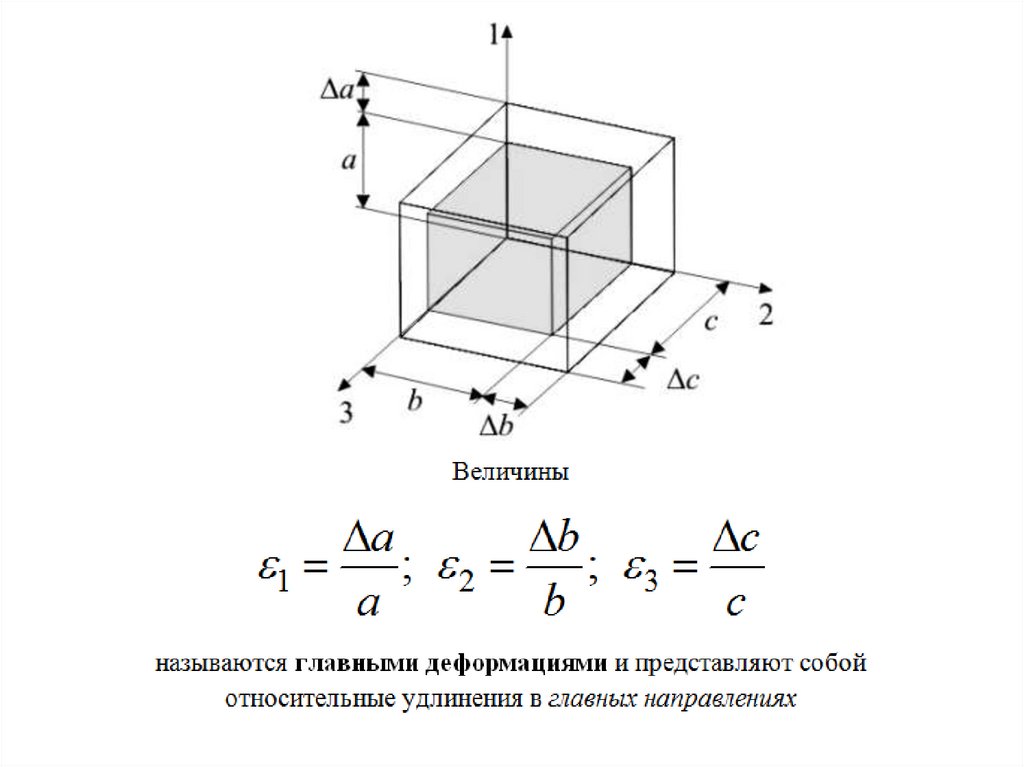
25.

1'
1
;
1''
2
;
1'''
3
E
E
E
Сложив эти величины, будем иметь
1
2
3
1
1
1 2 3
E
E
E E

26.

Обобщенный закон Гука
для изотропного тела:
зависимость между линейными деформациями
и главными напряжениями
1
1 1 2 3 ;
E
1
2 2 1 3 ;
E
1
3 3 1 2
E

27.

Выражения справедливы
и для относительных деформаций
по любым трем взаимно перпендикулярным
направлениям
1
x [ x ( y z )];
E
1
y [ y ( z x )];
E
1
z [ z ( x y )]
E

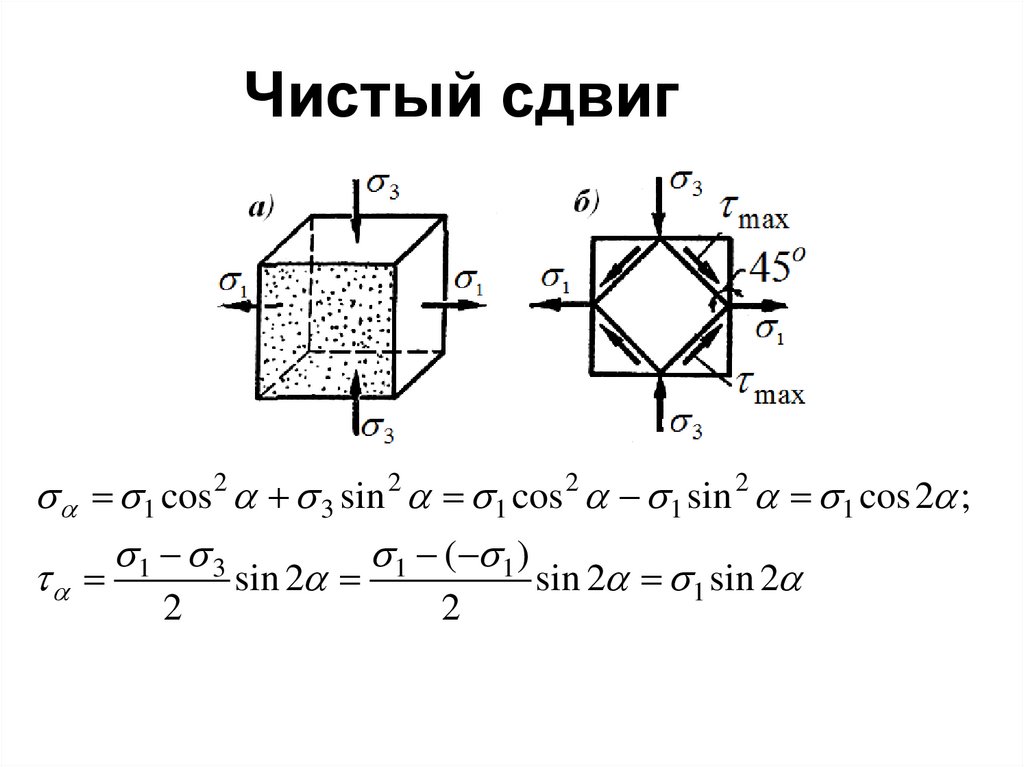
28. Чистый сдвиг

1 cos 2 3 sin 2 1 cos 2 1 sin 2 1 cos 2 ;
1 3
1 ( 1 )
sin 2
sin 2 1 sin 2
2
2

29.

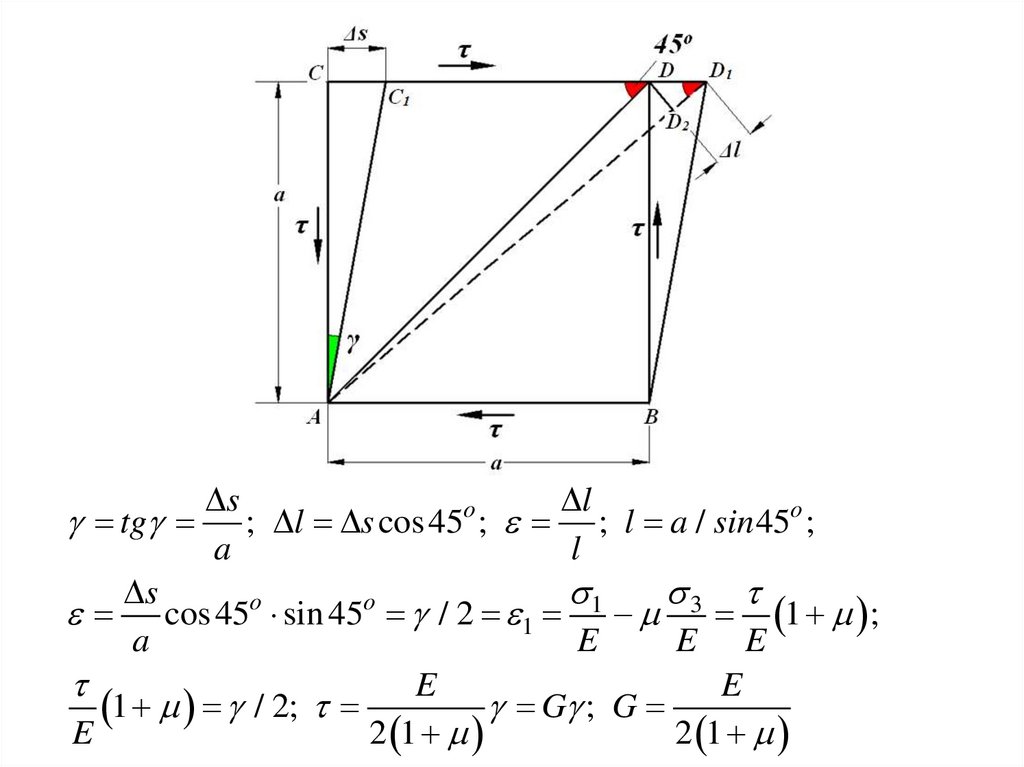
Деформации при чистом сдвиге

30.

s
l
o
tg ; l s cos 45 ; ; l a / sin 45o ;
a
l
3
s
1
o
o
cos 45 sin 45 / 2 1
1 ;
a
E
E E
E
E
1
/
2;
G
;
G
E
2 1
2 1

31. Модуль сдвига G (модуль упругости второго рода)

Е – модуль Юнга
E
G
2(1 )
(модуль упругости первого
рода)
- коэффициент
Пуассона

32. Основные понятия о гипотезах прочности

33. Предельное напряженное состояние – мера прочностных свойств материала, при котором происходит переход от одного механического

состояния к другому
Предельное напряжение определяют
при механических испытаниях
данного материала
на одноосное растяжение и сжатие

34.

Коэффициент запаса прочности
n
равен отношению предельного
напряжения к рабочему (расчетному)
n пред / расч

35.

Напряженные состояния, для которых
отношения главных напряжений
одинаковы, называют
подобными
/ / / /
I
1
I
2
I
3
II
1
II
2
II
3

36. Коэффициент запаса прочности

- величина, показывающая, во сколько
раз нужно увеличить возникающие в
исследуемой точке главные
напряжения для того, чтобы
напряженное состояние стало
предельным

37. Равноопасными называются такие напряженные состояния, для которых коэффициенты запаса прочности равны

• Это дает возможность
сравнивать все
напряженные состояния
между собой, заменяя
их равноопасным
одноосным
напряженным
состоянием
(растяжением)
• Эквивалентное
напряжение напряжение, которое
следует создать в
растянутом образце,
чтобы его напряженное
состояние стало
равноопасным
заданному
напряженному
состоянию

38.

39. Определение эквивалентных напряжений по различным гипотезам прочности

40.

ПЕРВАЯ ГИПОТЕЗАГипотеза наибольших нормальных напряжений
(предложена Галилеем):
«Причиной разрушения материала являются
наибольшие по абсолютному
значению нормальные напряжения»
Условие прочности
I
экв
1 р

41.

Если наибольшим по значению будет
сжимающее главное напряжение,
условие прочности по первой гипотезе прочности:
I
экв
3 сж

42.

Недостаток первой гипотезы прочности:
не учитываются два других главных напряжения,
оказывающих влияние на прочность материала.
Первая гипотеза прочности подтверждается
экспериментальными данными только для
хрупкого материала при растяжении,
когда напряжения 2 , 3
значительно меньше 1

43.

При всестороннем сжатии цементного кубика,
первая гипотеза прочности приводит к ошибочным
результатам,
поскольку кубик выдерживает напряжения,
во много раз превышающие предел прочности при
одноосном сжатии.
В настоящее время первая гипотеза прочности не
применяется и имеет лишь историческое значение

44.

Гипотеза наибольших линейных деформаций
(предложена Мариоттом и развита Сен-Венаном):
«Причиной разрушения материала являются
наибольшие линейные деформации»
Эквивалентные напряжения вычисляются по формуле
II
экв
1 2 3 ,
где коэффициент Пуассона

45.

Считается, что для пластичных материалов
закон Гука выполняется вплоть до предела текучести,
а для хрупких – до предела прочности,
что является грубым допущением.
Достоинством второй гипотезы прочности является то, что
при вычислении эквивалентного напряжения
она учитывает все три главных напряжения.
С помощью гипотезы наибольших линейных деформаций
можно объяснить разрушение хрупких материалов при простом
сжатии. Однако вторая гипотеза прочности недостаточно
подтверждается опытами и не применяется

46. Гипотеза наибольших касательных напряжений (предложена Треска)

«Два напряженных состояния равноопасны,
если максимальные касательные напряжения для
них одинаковы»
max 1 3 / 2; экв экв / 2;
max экв ;
III
экв
1 3

47.

Недостаток гипотезы:
не учитывается второе главное напряжение.
Однако, опыты показывают, что
для пластичных материалов гипотеза
наибольших касательных напряжений дает
удовлетворительные результаты.
Ошибка от пренебрежения влиянием
второго главного напряжения
не превышает 10 – 15 %

48. Гипотеза удельной потенциальной энергии изменения формы (предложена фон Мизесом)

«Два напряженных состояния равноопасны,
если удельная потенциальная энергия
изменения формы для них одинакова»
IV
экв
1
2
2
2
[( 1 2 ) ( 2 3 ) ( 3 1 ) ] [ ]
2

49.

ГИПОТЕЗА ПРОЧНОСТИ МОРА:
Два напряженных состояния равноопасны,
если для соответствующих главных напряжений
соблюдается соотношение:
1' 3' 1'' 3'' [ ].
пч ( раст )
для пластичных материалов.
пч ( сж )
Для хрупких 1.

50.

Гипотеза прочности Мора рекомендуется
для хрупких материалов.
Для пластичных материалов
гипотеза тождественна
третьей гипотезе прочности

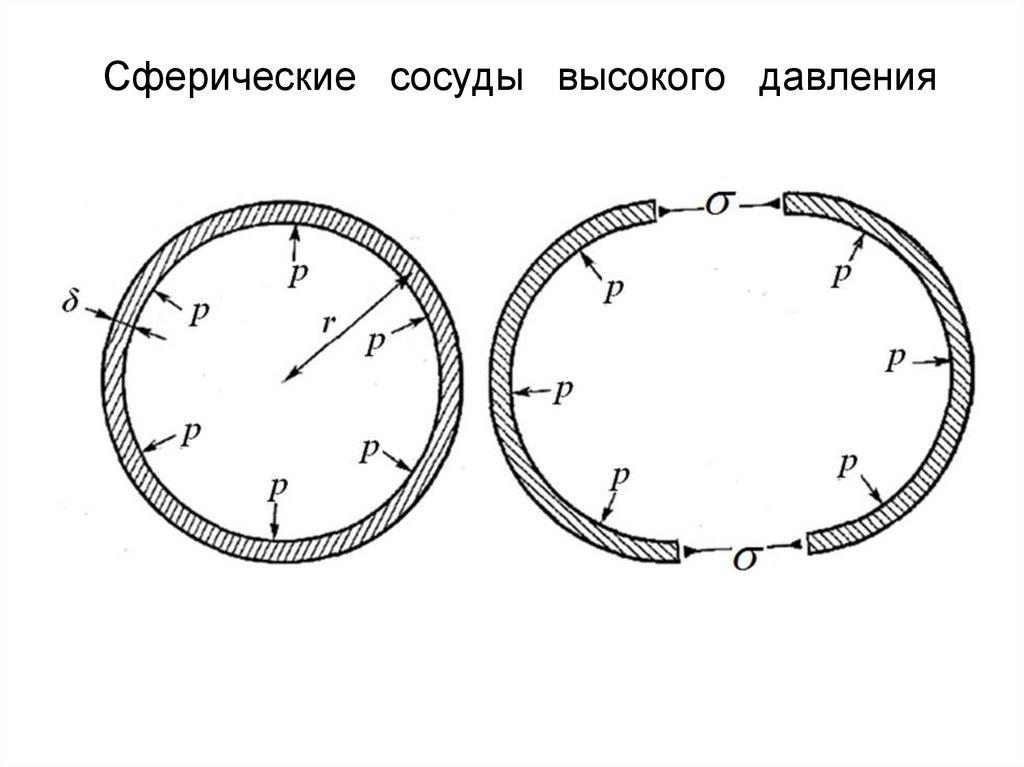
51. Сферические сосуды высокого давления

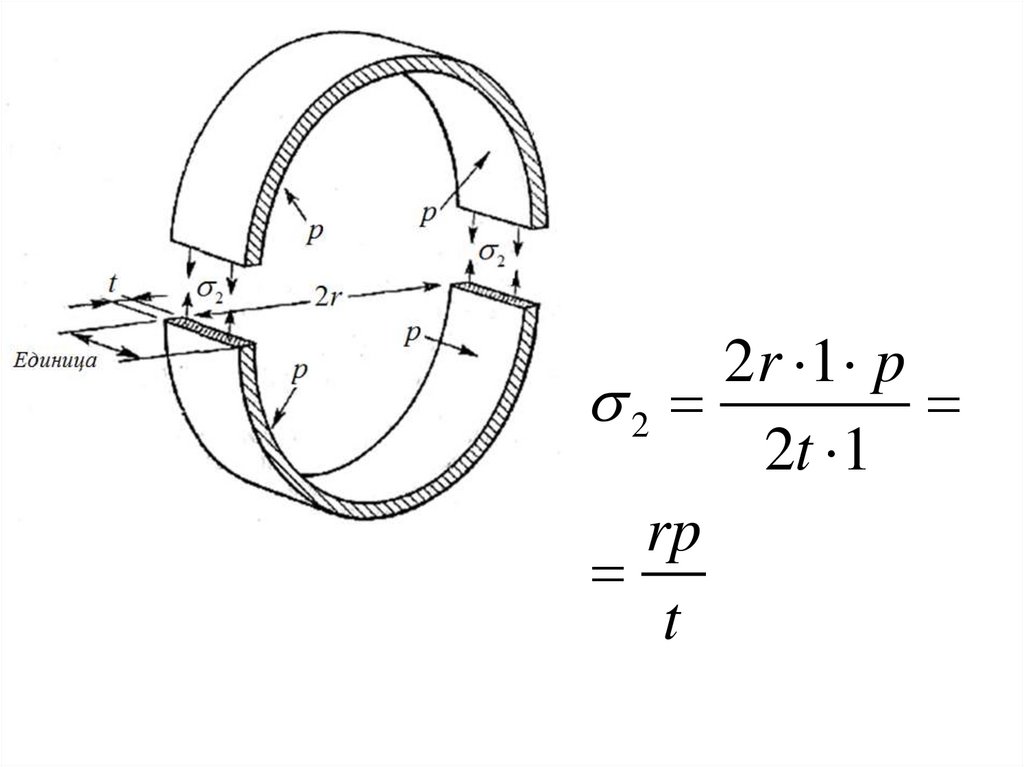
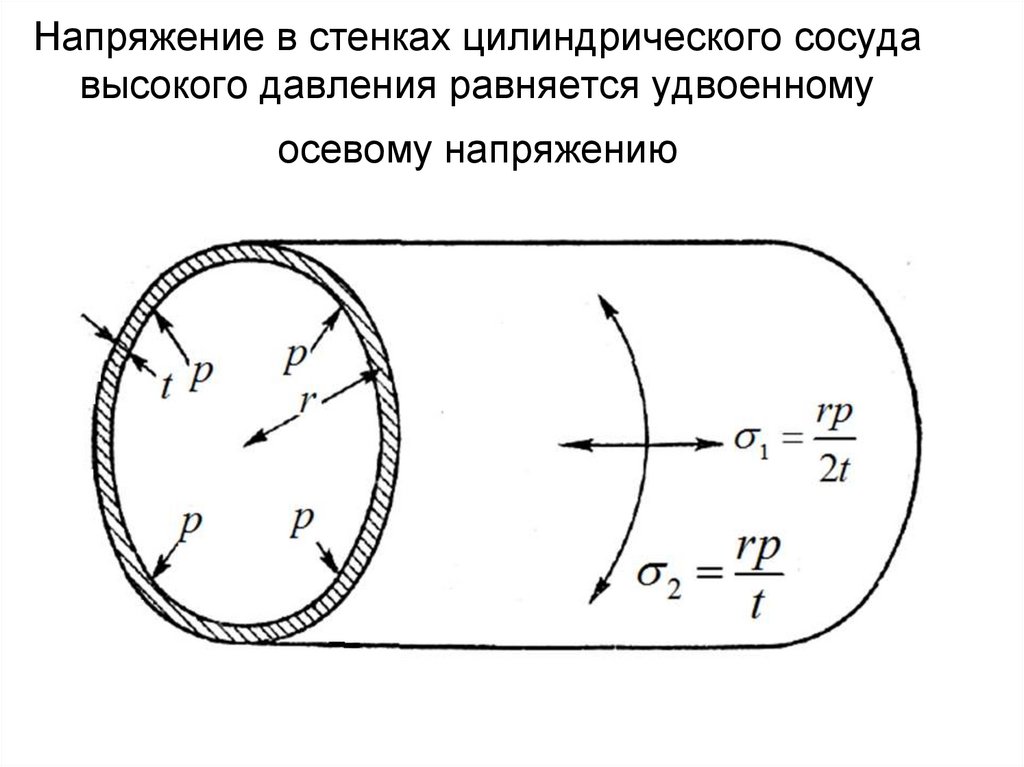
52. Цилиндрические сосуды высокого давления

r p rp
1
2 rt 2t
2

53.

2r 1 p
2
2t 1
rp
t

54. Напряжение в стенках цилиндрического сосуда высокого давления равняется удвоенному осевому напряжению

55.

Одно из следствий этого мог наблюдать
каждый, кто хоть однажды отваривал
сосиски
Когда содержимое сосиски
чрезмерно разбухает
и шкурка лопается,
разрыв всегда бывает продольным