Similar presentations:
Напряженное и деформированное состояния элемента в окрестности точки
1.
ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»Инженерно-технический институт
Кафедра прикладной механики
Лекции
по дисциплине «Техническая механика»
270800 - Строительство
2. НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЯ ЭЛЕМЕНТА В ОКРЕСТНОСТИ ТОЧКИ
3.
Напряженное состояние элементов в окрестности точкиНапряженным состоянием в точке называется совокупность
напряжений, действующих по всевозможным площадкам, проведенным
через эту точку.
В общем случае в теле элемента
конструкции напряженное состояние
неоднородно, оно меняется от точки
к точке. При изучении напряженного
состояния в какой-либо точке «К»
мысленно вырезают в окрестности
этой точки параллелепипед со
сторонами dX, dY, dZ, на гранях
которого действуют нормальные и
касательные напряжения.
z
z
zx
zy
x
y
y
yz
yx
z
y
xz
xy
x
x
4.
Компоненты напряжений в окрестности рассматриваемой точки:x, y, z – нормальные напряжения на площадках с нормалями X,Y,Z
соответственно;
xy, xz, yx, yz, zx, zy – касательные напряжения на тех же площадках.
Первые индексы показывают принадлежность, т.е. площадки, на которых
действуют, а вторые на направления.
- тензор напряжений в окрестности
рассматриваемой точки
Закон парности касательных напряжений.
Если на какой-либо площадке действует касательное напряжение, то на
ортогональной (перпендикулярной) к ней площадке действует такое же по
величине и противоположное по направлению касательное напряжение.
По закону парности касательных напряжений имеем xy= yx, yz= zy, xz= zx.
5.
Главные площадки и напряжения. В любой точке нагруженного телавсегда можно выделить три ортогональные площадки, свободные от
касательных напряжений, которые называются главными площадками.
Действующие на них нормальные напряжения – главными напряжениями
в окрестности рассматриваемой точки и обозначаются 1, 2, 3.
(принято 1> 2> 3).
Напряженное состояние тела разделяют на три вида:
- линейное,
-плоское,
-объемное
Линейное напряженное состояние – окрестности рассматриваемой точки
можно провести только одну площадку, на которой действует нормальное
напряжение, а на двух других ортогональных площадках напряжения равны
нулю.
1
3
3
n
1
1
1
1
6.
Определение напряжений в наклонном сечении растянутых (сжатых)стержней. Усилия по наклонным площадкам при растяжении (сжатии)
бруса определяются методом сечения. Равновесие отсеченной части (рис.
б): Z I 0 S P1 P2 ,
б)
a)
P2
P1
P4
в)
P2
P1
P2
P3
n
n
p
n
P1
P3
S
p
S
P4
S
S
N
cos cos cos ,
An A
A
A
;
cos
2
где Аn – площадь наклонного сечения; n p cos cos ;
А – площадь поперечного сечения;
где An
n p sin cos sin
2
sin 2 ,
р – полное напряжение на наклонном сечении;
n и n – нормальное и касательное составляющие полного напряжения р.
7.
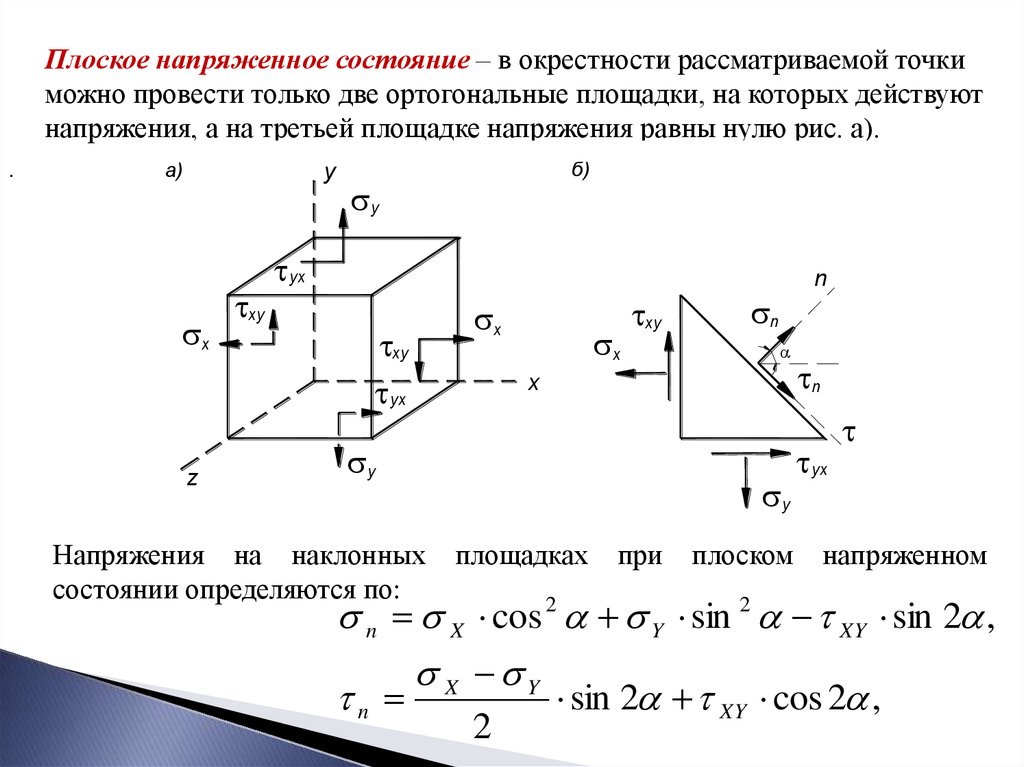
Плоское напряженное состояние – в окрестности рассматриваемой точкиможно провести только две ортогональные площадки, на которых действуют
напряжения, а на третьей площадке напряжения равны нулю рис. а).
.
y
a)
x
z
xy
б)
y
yx
xy
yx
x
x
xy
n
x
y
Напряжения на наклонных
состоянии определяются по:
n
y
площадках
при
плоском
n
yx
напряженном
n X cos 2 Y sin 2 XY sin 2 ,
X Y
n
sin 2 XY cos 2 ,
2
8.
Двухосное растяжениеРазноименное плоское
напряженное состояние
1
1
2
3
3
2
2
3
1
Двухосное сжатие
2
3
1
Закон постоянства суммы нормальных напряжений
1 cos 2 2 sin 2
1 sin 2 2 cos 2
1 cos 2 2 sin 2 1 sin 2 2 cos 2 1 2
На двух взаимно перпендикулярных площадках сумма
нормальных напряжений величина постоянная, которая не
зависит от положения выбранных площадок.
9.
.Определение главных напряжений и положения главных площадок
при плоском напряженном состоянии.
Из условия, что на главных площадках касательные напряжения равны
2 XY
нулю ( n=0), определим положение главных площадок:
tg 2 0
X Y
Величины главных нормальных напряжений i определяются из
предыдущих формул n , когда = 0 и =( 0+900): ( n = i )
i X cos 2 0 Y sin 2 0 XY sin 2 0 ,
0
i
2
2
sin
cos
0 XY sin 2 0 .
0
X
0
Y
0 90
Величины главных напряжений являются экстремальными значениями
нормальных напряжений в окрестности рассматриваемой точки:
n
X Y 1
0, отсюда i max
2
2
min
2
X Y 2 4 XY
10.
Когда плоское напряженное состояние представлено через главныенапряжения, то напряжения на наклонной площадке определяются:
n 1 cos 2 2 sin 2 ,
1 2
n
sin 2 .
или
n
1 2
2
2
1 2
2
cos 2
Экстремальные значения касательных напряжений в окрестности
рассматриваемой точки плоского элемента равны полу-разности главных
напряжений и действуют на площадках, наклоненных к главным площадкам
на угол 450.
1 2
max
min
max
min
1
2
или
2
X
Y 4 XY ,
2
а действующие на этих площадках нормальные напряжения равны:
45
0
1 2
2
X Y
2
11.
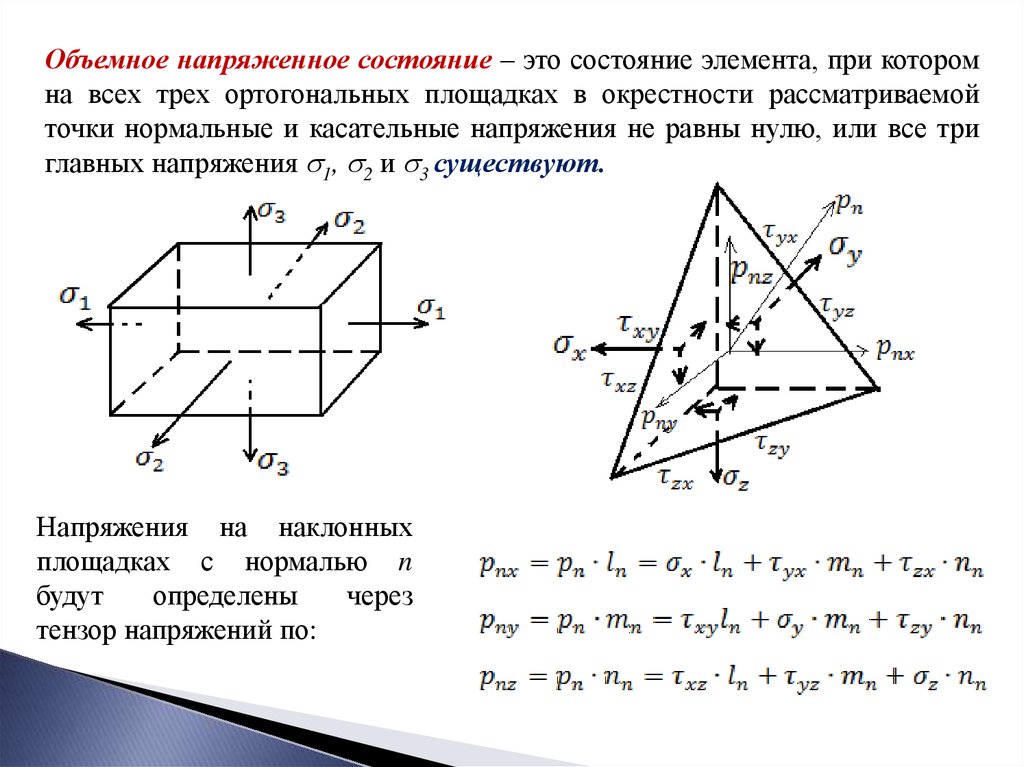
Объемное напряженное состояние – это состояние элемента, при которомна всех трех ортогональных площадках в окрестности рассматриваемой
точки нормальные и касательные напряжения не равны нулю, или все три
главных напряжения 1, 2 и 3 существуют.
Напряжения на наклонных
площадках с нормалью n
будут
определены
через
тензор напряжений по:
12.
Если полное напряжение на рассматриваемой площадке равно главномунапряжению
, то имеем матричное уравнение:
X i li YX mi ZX ni 0,
XY li Y i mi ZY ni 0,
l m n 0
YZ i
Z
i
i
XZ i
Раскрывая определитель матрицы
получаем кубическое уравнение
3 I 1 2 I 2 I 3 0
Коэффициентами уравнения являются инварианты напряженного состояния:
I1 X Y Z
– первый инвариант;
2
2
2
I 2 X Y X Z Y Z XY
XZ
YZ
– второй инвариант;
2
2
2
I 3 X Y Z X YZ
Y XZ
Z XY
2 XZ YZ XY
третий инвариант.
13.
Определение положения главных площадокПоложения главных площадок определяются из совместного решения
однородной системы уравнений относительно неизвестных направляющих
косинусов li , mi , ni .
X i li YX mi ZX ni 0,
XY li Y i mi ZY ni 0,
l m n 0
YZ i
Z
i
i
XZ i
и зависимости
li2 mi2 ni2 1
Напряжения по наклонным площадкам относительно главных площадок,
определяются:
n 1 cos 2 2 cos 2 3 cos 2
n 12 cos 2 22 cos 2 32 cos 2 n2 ,
где , , - углы между нормалью n
рассматриваемой площадки и осями I,II,III
(направлениями главных напряжений).
14.
Октаэдрическая площадка – это площадка, нормаль к которой составляетравные углы с направлениями всех трех главных напряжений, 1= 2= 3.
a)
окт
3
б)
Нормальное
напряжение
на этой площадке равно
среднему напряжению: 2
2
1
1
окт
45°
окт
max
1
1 2 3 ср
3
1
Касательное напряжение определяется:
2 1
окт
3
max
3
1 2 2 2 3 2 3 1 2
3
напряжения
a) касательные
Максимальные
окт
3
б)
Максимальное касательное напряжение
в
2
данной
точке
равно
полу-разности
максимального и 1минимального главных 1
напряжений и действует окт
на площадке,
наклоненной к ним под углом 450:
3
2
45°
max
1
max
2
3
max
1 3
2
15.
Деформированное состояние элементовв окрестности точки
Совокупность относительных удлинений и углов сдвига для
всевозможных направлений осей, проведенных через данную точку,
называется деформированным состоянием в точке.
Компоненты деформаций в трех ортогональных плоскостях
представляются через X, Y, Z – линейные относительные деформации
(относительные удлинения, укорочения) по осям X, Y, Z и
углы
сдвига
элемента
в
ij i X , Y , Z ; j X , Y , Z ; i j –
соответствующих плоскостях OXY, OXZ и OYZ.
Деформированное состояние элементов выражается тензором деформаций
16.
dzДеформация граней
элемента в плоскости OXZ
xy= yx,
xz= zx,
yz= zy.
Связь между напряжениями и
деформациями в точке
(обобщенный закон Гука)
/2
dz
xz
Аналогично закону парности
касательных напряжений имеем
zx
/2
dx
dx
Если известны компоненты напряжений, то
элементы компонентов деформаций определяются
из закона Гука.
При объемном напряженном состоянии:
XY
1
X X Y Z , XY
,
E
G
1
Y Y X Z , XZ XZ ,
E
G
YZ
1
Z Z X Y , YZ
.
E
G
17.
11 1 2 3 ,
E
1
2 2 1 3 ,
E
1
3 3 1 2 .
E
Если
компоненты
напряжений
представлены
через
главные
напряжения 1, 2, 3, то главные
относительные деформации:
При плоском напряженном состоянии:
Или через главные напряжения:
1
X X Y ,
E
1
Y Y X ,
E
Z
E
X
Y ,
XY
XY
G
,
1
1 1 2 ,
E
1
2 2 1 ,
E
3
E
1 2 .
18.
Еслиизвестны
компоненты
деформаций
в
окрестности
рассматриваемой точки, то элементы тензора напряжений при объемном
деформированном состоянии определяются по обратному закону Гука:
X 2G X ,
Y 2G Y ,
Z 2G Z ,
XY G XY ,
YZ G YZ ,
ZX G ZX ,
или через главные деформации:
1 2G 1 ,
2 2G 2 ,
3 2G 3 .
X Y Z 1 2 3 3 ср
– относительное изменение объема.
2 G
1 2
– коэффициент Ляме;
19.
Изменение объема материала при упругой деформацииИзменение объема элементарного параллелепипеда в процессе деформации
будет:
V V0 X Y Z V0 1 2 3
Относительное изменение объема (относительная объемная деформация)
определяется:
V
V0
X Y Z 1 2 3
или через напряжения:
1 2
1 2
X Y Z
1 2 3
E
E
Удельная потенциальная энергия упругой деформации:
u
1 1
2
2 2
2
3 3
2
Дж
3 , или
м
1
u
12 22 32 2 1 2 2 3 3 1 .
2E
20.
Потенциальная энергия изменения объема при упругой деформации:.
u об
1 2
2
1 2 3
6E
Потенциальная энергия изменения формы при упругой деформации:
1 2
uф
1 22 32 1 2 2 3 3 1
3E
21.
Теории прочностиТеория прочности базируется на гипотезе, что одноосное напряженнодеформированное состояние тел оказывается по степени опасности
эквивалентно рассматриваемому сложному напряженно-деформированному
состоянию.
Прочность материала при сложном напряженном состоянии
оценивается функцией Ф( 1 2 3)=С – const.
1.Теория наибольших растягивающих напряжений
Наибольшие растягивающие напряжения в теле
превышать допускаемого напряжения при растяжении:
экв . 1
1
в
к
не
должны
p
где к – коэффициент запаса прочности материала при растяжении.
Теория наибольших растягивающих напряжений достаточно
достоверно оценивает прочность хрупких материалов.
22.
2.Теория наибольших относительных растягивающих деформацийНаибольшие относительные растягивающие удлинения в теле
элемента не должны превышать допустимого значения относительных
деформаций при растяжении для данного материала:
1 p
По данной теории прочности оцениваются повреждаемость элементов,
подверженных деформации ползучести и малоцикловому нагружению.
Выражая деформации через напряжения, получим:
экв . 1 2 3
2
в
к
p
По этой формуле могут быть оценены прочность очень хрупких
материалов, у которых практически отсутствуют остаточные деформации
(керамика и т.п.).
23.
3.Теория наибольших касательных напряженийНаибольшие касательные напряжения в теле элемента не должны
превышать допустимого значения касательных напряжений для данного
материала:
или через главные напряжения условие прочности по третьей теории
оценивается:
экв.3 1 3
или если упругопластичный материал имеет разные прочности при
растяжении и сжатии
экв . 1 p 3 теория Мора,
3
где
p
p
сж
24.
4.Энергетическая теория прочностиНачало текучести или разрушения материала элемента наступает тогда,
когда потенциальная энергия формоизменения
достигает предельного
.
значения:
uф uф
Условие прочности материала по четвертой теории:
экв .
4
т
1
2
2
2
1 2 2 3 3 1
2
к
Такая же формула получается из теории октаэдрических касательных
напряжений:
экв
4
1
3
2
2
2
1 2 2 3 3 1 окт
2
2
25.
Применение полученных формул при проверке прочности материалаэлементов конструкции при простейших видах деформаций
Проверка прочности элементов, работающих на чистый сдвиг.
При чистом сдвиге по граням элемента действуют только касательные
напряжения. Положение главной площадки при чистом сдвиге определяется:
2
2
tg 2 0
,
X Y
0
т.е. главные площадки лежат под углом 450 к рассматриваемым
площадкам.
Величины главных напряжений при чистом сдвиге:
X Y
1
1,3
2
2
1 , 3 .
X
2
Y 4 XY
2
26.
Кручение круглого стержня=
=
27.
Проверка прочности элементов, работающих на чистый сдвигпо различным теориям прочности.
По наибольшим растягивающим напряжениям:
экв 1 p ,
1
т.е. допускаемое касательное напряжение
нормальному напряжению при растяжении
равно
p
допускаемому
1
По теории наибольших относительных деформаций:
экв 1 3 1 p , отсюда II
2
По теории наибольших касательных напряжений:
экв 1 3 2 ,
3
По энергетической теории прочности:
экв
4
p
1
отсюда III 0,5
1
1 2 2 2 3 2 3 1 2 3 2 3 ,
2
IV 0,577 .
отсюда

























 mechanics
mechanics








