Оценка качества регулирования. Радиоавтоматика. Лекция 7

1.

РАДИОАВТОМАТИКА
Лекция 7
ОЦЕНКА КАЧЕСТВА
РЕГУЛИРОВАНИЯ

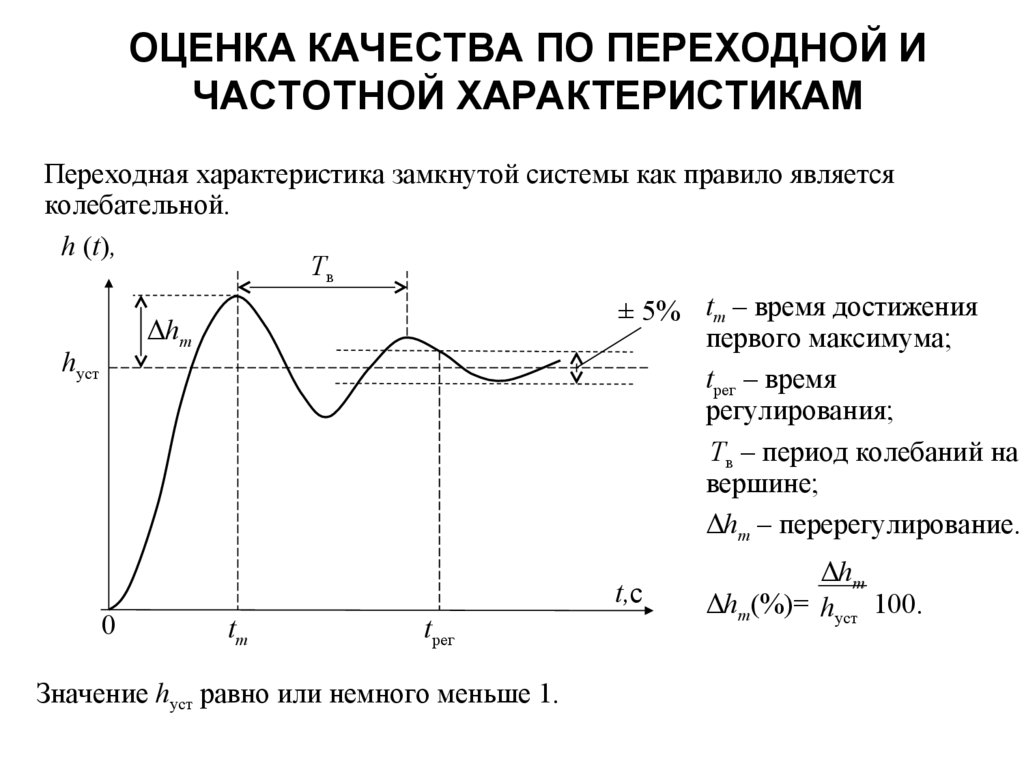
2. ОЦЕНКА КАЧЕСТВА ПО ПЕРЕХОДНОЙ И ЧАСТОТНОЙ ХАРАКТЕРИСТИКАМ

Переходная характеристика замкнутой системы как правило является
колебательной.
h (t),
Tв
± 5% tm – время достижения
Δhm
первого максимума;
hуст
tрег – время
регулирования;
Tв – период колебаний на
вершине;
Δhm – перерегулирование.
t,c
0
tm
tрег
Значение hуст равно или немного меньше 1.
Δhm
Δhm(%)= hуст 100.

3.

Km
K0
L(ω), дБ φ(ω), рад
Kз(ω)
НЧ
НЧ
60
40
ВЧ
0
ω, рад/с
ωm
Показатель колебательности
Km
M
K0
K0 близок к 1 и M ≈ Km
20
ωср
-20 -π/2
-40 -π
Область НЧ: Lр(ω) >> 0, Kр(ω) >> 1, Kз(ω) =
ω, рад/с
Lр(ω)
Δφ
| Kр(jω) |
≈ 1.
| 1 + Kр(jω) |
ВЧ
φр(ω)
| Kр(jω) |
Область ВЧ: Lр(ω) << 0, Kр(ω) << 1, Kз(ω) =
≈ Kр(ω) << 1
| 1 + Kр(jω) |

4.

Область СЧ: – (20 - 30) дБ < Lр(ω) < (30 - 40) дБ
1
| Kр(jωср) |
Kз(ωср) =
=
.
–j(π – Δφ)
|
1
+
e
|
| 1 + Kр(jωср) |
1) Δφ = 90o = π/2
1
Kз(ωср) =
.
| 1 + e–jπ/2|
Im
1 Re
2) Δφ = 60o = π/3
1
Kз(ωср) =
.
| 1 + e–j2π/3|
Im
3) Δφ = 30o = π/6
1
Kз(ωср) =
.
| 1 + e–j5π/6|
Im
1 Re
e–j2π/3
1 Re
e–j5π/6
e–jπ/2
| 1 + e–jπ/2 | = √2 .
Kз(ωср) = 1 / √2 ≈ 0,7.
| 1 + e–j2π/3 | = 1.
Kз(ωср) = 1 / 1 = 1
| 1 + e–j5π/6 | = 2sin(π/12) ≈ 2π/12.
Kз(ωср) = 12 / 2π ≈ 2.

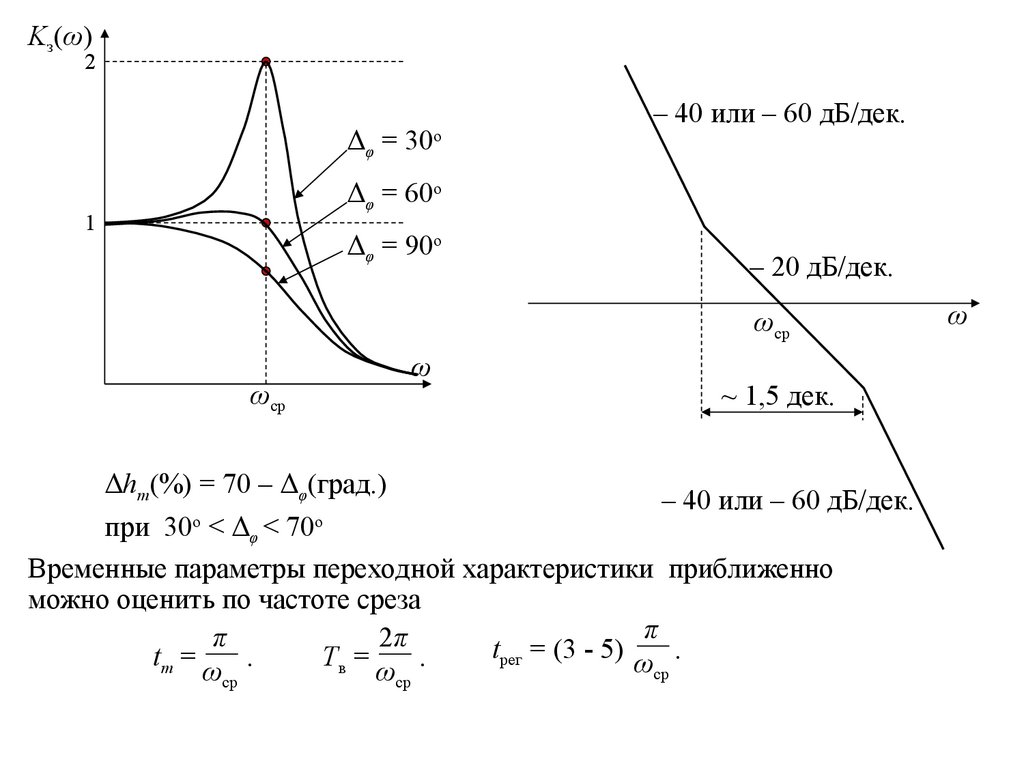
5.

Kз(ω)
2
Δφ = 30
o
– 40 или – 60 дБ/дек.
Δφ = 60o
1
Δφ = 90o
– 20 дБ/дек.
ωср
ωср
ω
~ 1,5 дек.
Δhm(%) = 70 – Δφ(град.)
– 40 или – 60 дБ/дек.
о
o
при 30 < Δφ < 70
Временные параметры переходной характеристики приближенно
можно оценить по частоте среза
π
π
2π
t
=
(3
5)
.
рег
tm =
.
Tв =
.
ω
ср
ωср
ωср
ω

6.

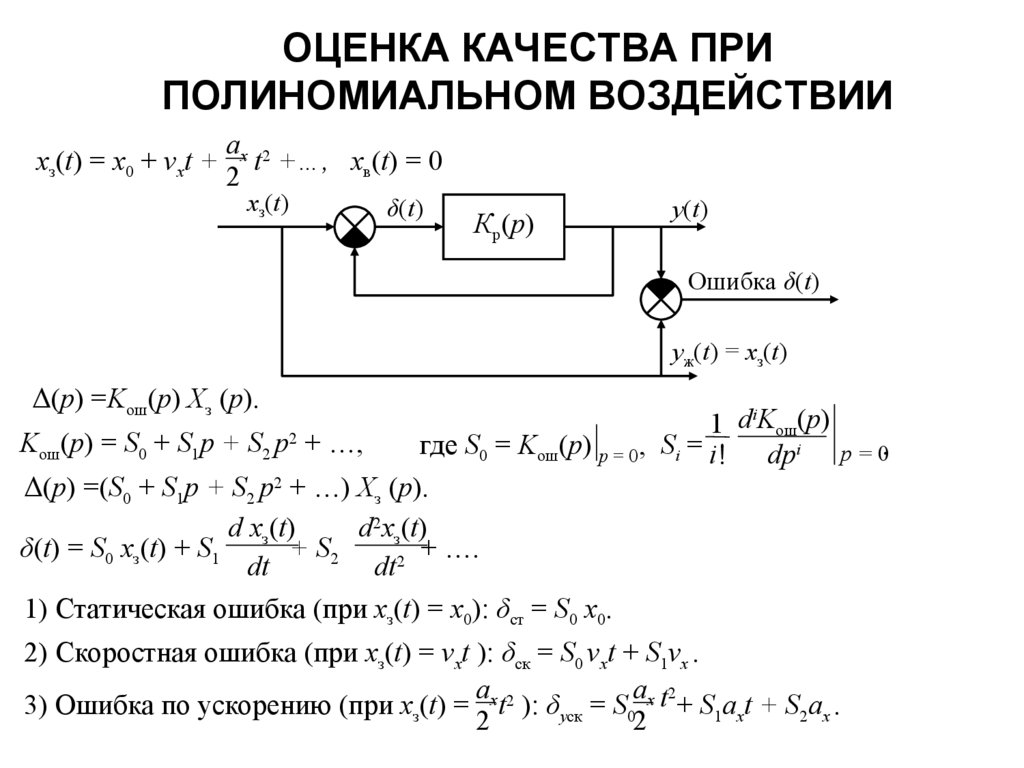
ОЦЕНКА КАЧЕСТВА ПРИ
ПОЛИНОМИАЛЬНОМ ВОЗДЕЙСТВИИ
xз(t) = x0 + vxt +
ax 2
t +…, xв(t) = 0
2
xз(t)
δ(t)
Кр(р)
y(t)
Ошибка δ(t)
yж(t) = xз(t)
Δ(p) =Kош(p) Xз (p).
diKош(p)
1
Kош(p) = S0 + S1p + S2 p2 + …,
где S0 = Kош(p) p = 0, Si = i! dpi
Δ(p) =(S0 + S1p + S2 p2 + …) Xз (p).
d xз(t)
d2xз(t)
δ(t) = S0 xз(t) + S1
+ S2
+ ….
2
dt
dt
1) Статическая ошибка (при xз(t) = x0): δст = S0 x0.
p = 0.
2) Скоростная ошибка (при xз(t) = vxt ): δск = S0 vxt + S1vx .
a
a 2
3) Ошибка по ускорению (при xз(t) = x t2 ): δуск = S0 x t + S1axt + S2ax .
2
2

7.

Для расчета ошибок нужно знать три первых коэффициента разложения: S0, S1, S2.
bmpm + bm-1 pm-1 + … + b0
Kр(p) =
, n≥m
anpn + an-1 pn-1 + … + a0
anpn + an-1 pn-1 + … + a0
1
Kош(p) =
=
.
1+ Kр(p)
anpn + … + am+1 pm+1 + (am + bm) pm + … + (a0 + b0)
S0 = Kош(p)
p ==
0
a0
.
a0 + b0
dKош(p) (…+2a2p+a1)(…+(a1+b1)p+(a0+ b0)) – (…+a1p+a0)(…2(a2+b2)p+ (a1+b1))
=
dp
(… + (a1 + b1) p + (a0 + b0))2
dKош(p)
a1(a0+ b0) – a0 (a1+b1)
a 1b 0 – a 0 b 1
S1 =
=
=
.
2
2
dp
(a0 + b0)
(a0 + b0)
p=0
1 d2Kош(p)
S2 =
dp2
2!
=
p=0
(a2b0 – a0b2)(a0+ b0) – (a1b0 – a0b1)(a1+b1)
(a0 + b0)3
САР называется статической, если коэффициент S0 отличен от нуля и
астатической, если равен нулю.
Количество первых нулевых коэффициентов определяет порядок астатизма.

8. ОШИБКИ В СТАТИЧЕСКИХ И АСТАТИЧЕСКИХ СИСТЕМАХ

1) СТАТИЧЕСКАЯ СИСТЕМА
S0 =
a0
.
a0 + b0
x=
vx t
S0 ≠ 0 → a0 ≠ 0 .
bmpm + bm-1 pm-1 + … + b0
Kр(p) =
.
anpn + an-1 pn-1 + … + a0
b0
Коэффициент передачи разомкнутой системы: K = Kр(0) =
.
a0
1
1
a0 =
Тогда S =
=
.
0
1
+
b
/a
1
+
K
0 0
a0 + b0
Статическая ошибка
Скоростная ошибка
Ошибка по ускорению
x0
vxt
axt2
δст=
.
δск=
+ S1vx.
δуск=
+ S 1a x t + S 2 a x .
1+K
1+K
1+K
x y
x y
δст x = x
Область применения статических
0
y = x0 – δст
0
t
δск
0
)
y( t
t
систем ограничивается только
системами стабилизации,
поддерживающими постоянной
регулируемую величину.

9.

2) АСТАТИЧЕСКАЯ СИСТЕМА ПЕРВОГО ПОРЯДКА
S0 = 0 → a0 = 0 .
a0
S0 =
. a 0 + b0
a b – a0b1
S1 = 1 0
(a0 + b0)2
y(
t)
=
vx t
-δ
x=
ск
vx t
bmpm + bm-1 pm-1 + … + b0
bmpm + bm-1 pm-1 + … + b0
Kр(p) =
=
anpn + an-1 pn-1 + … + a1p p(anpn-1 + an-1 pn-2 + … + a1)
Замкнутая система является астатической первого порядка,
если в разомкнутую входит один интегратор.
b
b0
Kр(p)
= 0
Коэффициент
передачи
разомкнутой
системы:
K
=
[1/c] .
a1p
a
1
p→0
a1 1
Тогда S1 =
=
.
b0 K
Статическая ошибка
Скоростная ошибка
Ошибка по ускорению
v
at
δст= 0
δск= x .
δуск= x +
K
K
.
S 2ax .
x y
x y
δст=0 x = x
0
Астатические системы первого
y = x0
порядка из-за постоянства
δск
скоростной ошибки широко
используются в качестве следящих
t
t систем.
0
0

10.

3) АСТАТИЧЕСКАЯ СИСТЕМА ВТОРОГО ПОРЯДКА
S1 = 0 → a1 = 0 .
S0 = 0 → a0 = 0 .
a0
S0 =
. a 0 + b0
a b – a0b1
S1 = 1 0
(a0 + b0)2
δск=0
0
y( x =
t)
= vx t
vx t
bmpm + bm-1 pm-1 + … + b0
bmpm + bm-1 pm-1 + … + b0
Kр(p) =
=
anpn + an-1 pn-1 + … + a2p2 p2(anpn-1 + an-1 pn-2 + … + a2)
Порядок астатизма замкнутой системы равен количеству
интеграторов в разомкнутой системе.
b
b
Kр(p)
= 0 2 Коэффициент передачи разомкнутой системы: K = 0 [1/c2] .
ap
a2
p→0 2
a2 1
Тогда S2 =
=
.
b0 K
Статическая ошибка
Скоростная ошибка
Ошибка по ускорению
a
δст= 0
δск= 0
δск= x .
K
.
.
x y
Астатические системы второго
порядка используются в качестве
следящих систем при повышенных
требованиях к ошибке слежения.
t