Similar presentations:
Устойчивость сжатых стержней. Формула Эйлера
1. Лекция № 6
24.04.2020г.2.
Устойчивость сжатых стержней.Формула Эйлера.
После начала использования стали при построении
инженерных сооружений вопросы устойчивости гибких
сжатых стержней и тонкостенных конструкций получили
большое практическое значение.
2
3.
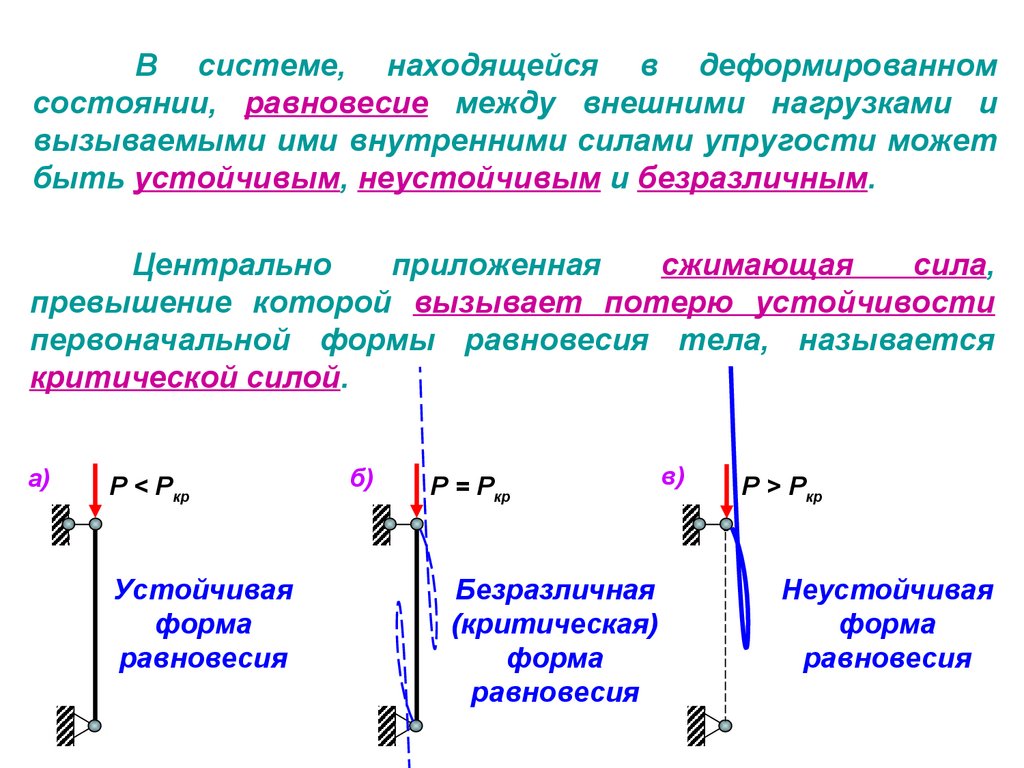
В системе, находящейся в деформированномсостоянии, равновесие между внешними нагрузками и
вызываемыми ими внутренними силами упругости может
быть устойчивым, неустойчивым и безразличным.
Центрально
приложенная
сжимающая
сила,
превышение которой вызывает потерю устойчивости
первоначальной формы равновесия тела, называется
критической силой.
а)
Р < Ркр
Устойчивая
форма
равновесия
б)
Р = Ркр
Безразличная
(критическая)
форма
равновесия
в)
Р > Ркр
Неустойчивая
форма
равновесия
4.
Неустойчиваяформа
равновесия
связана
с
неограниченным ростом деформаций и напряжений,
поэтому
при
превышении
сжимающей
силой
ее
критического значения конструкция разрушается.
Для обеспечения определенного запаса устойчивости
необходимо выполнение условия:
Р P
где:
P
- сжимающая сила;
P
Pкр
ny
- допускаемая нагрузка;
Pкр - критическая сила;
n y - коэффициент запаса устойчивости.
Продольным
изгибом
называется
изгиб
стержня,
вызванный потерей устойчивости прямолинейной формы
его равновесия.
При
потере
устойчивости
прогиб
произойдет
4
перпендикулярно к оси наименьшей жесткости стержня.
5.
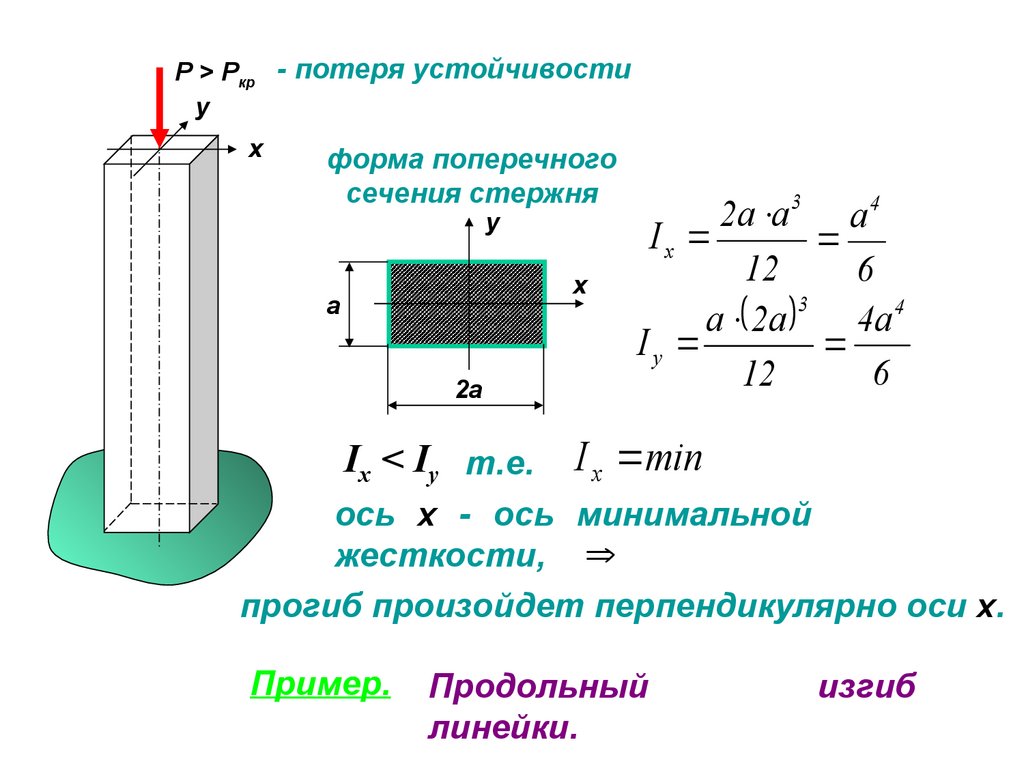
Р > Ркр - потеря устойчивостиy
x
форма поперечного
сечения стержня
y
x
а
2а
Ix < Iy т.е.
2а а 3 а 4
Ix
12
6
3
4а4
а 2а
Iу
6
12
I x min
ось х - ось минимальной
жесткости,
прогиб произойдет перпендикулярно оси х.
Пример.
Продольный
линейки.
изгиб
6.
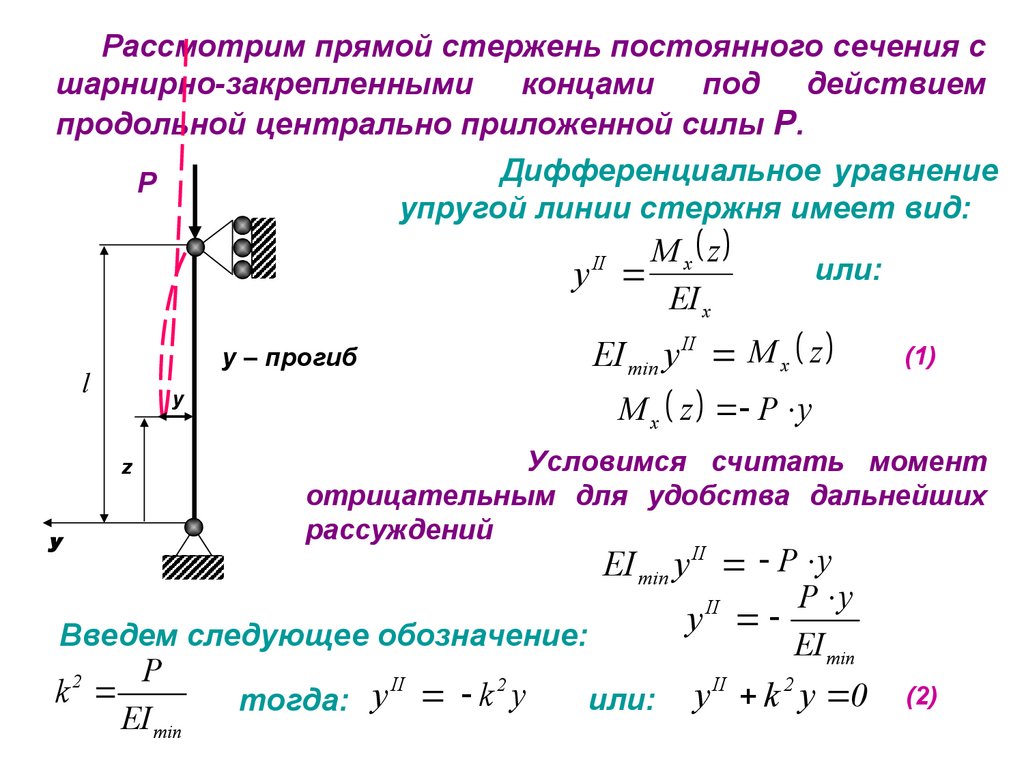
Рассмотрим прямой стержень постоянного сечения сшарнирно-закрепленными
концами
под
действием
продольной центрально приложенной силы Р.
Дифференциальное уравнение
Р
упругой линии стержня имеет вид:
M x z
у
EI x
II
у – прогиб
l
у
z
у
или:
EI min у II M x z
(1)
M x z P y
Условимся считать момент
отрицательным для удобства дальнейших
рассуждений
EI min у II P y
P y
II
у
Введем следующее обозначение:
ЕI min
P
2
II
2
II
2
k
или: у k y 0
тогда: у k y
ЕI min
(2)
7.
Решение уравнения (2) имеет вид:y ( z ) ACoskz BSinkz
(3)
Произвольные постоянные А и В
находим из граничных условий:
1)
y (0) 0
, т.е.
2)
y (l ) 0
, т.е.
0 ACosk 0 BSink 0 A
A 0
0 ACoskl BSinkl 0
BSinkl 0
B 0
или
(4)
, если
Sinkl 0
Если подставить А=0 и В=0 в (3), то: y ( z ) 0 , что не
соответствует условию задачи, следовательно: (4)
имеет корень Sinkl 0 .
8.
Т.к.P
k
ЕI min
тогда имеем:
P
l
n
EI min
P
Sinl
0 , откуда:
EI min
(5)
, где:
n 1, 2, 3...
Условие (5) выполняется и при n = 0, но тогда из него
следует, что Р = 0,что противоречит условию задачи.
Наименьшее значение
P Pкр 0
будет при n = 1, т.е.:
2
P
EI min
l
P
кр
2
EI min
l
(6)
критическая сила (сила Эйлера).
Впервые была получена Л.Эйлером в 1744г.
Леонард Эйлер (1707-1787гг.), математик. С 1730г. действительный
член Петербургской Академии наук. В механике занимался вопросами
продольной устойчивости сжатых стержней.
9.
Из (6) видно, что критическая сила не зависитот прочностных свойств материала.
Подставим (6) в
у ( z ) BSin
Итак:
у ( z ) BSinkz
n
т.е. в (3)
2
EI min
n z
z BSin
2
l EI min
l
n z
у ( z ) BSin
l
(7)
выражение прогиба от
действия силы Р.
Значение В в (7) характеризуется величиной
максимального прогиба уmax f , т.е. стрелой, когда
n z
Sin
1
l
n z
y f Sin
l
(8)
10.
Максимум y(z) имеет место при таком z, для которогоdy ( z )
n
n
n
f
Cos
z 0 , или Cos
z 0
dz
l
l
l
l
n
(9)
, или z
z
l
2
2n
dy ( z )
0
dz
n – число длин полуволн синусоиды, умещающихся на
длине стержня, испытывающего продольный изгиб.
n=1
n=4
Р
n=1
n=2
z l 2
z l4
n=3
n=2
- длина, на которой возникает уmax .
n=3
z l6
n=4
z 10l 8
11.
Влияние условий закрепленияконцов стержня
на величину критической силы.
Рассмотрим несколько вариантов закрепления
стержня длиной l и определим, сколько полуволн
умещается на его длине.
12.
а) стержень консольного типа.б) стержень шарнирно закрепленный по концам.
Изогнутая ось стержня а)
Р = Ркр
Р = Ркр
представляет
собой
половину
полуволны
синусоиды.
При сравнении его со стойкой
l
Эйлера - стержнем шарнирно
закрепленным по концам б),
видно, что их оси будут
2l
l
вести себя одинаково, если
длина первого будет равна
L=2l .
Определим Ркр из условия L=2l :
2
1
Pкр
2 EI min
2l
2
1
EI min
, n
2
2
4l
2
13.
в) стержень с одним жестко закрепленным концоми другим продольно-подвижным.
Р = Ркр
l
4
l
При потере устойчивости средняя
часть стержня длиной l изогнется
по синусоиде, как и стержень
длиной
L=l/2,
с
шарнирно
закрепленными концами.
l
2
Определим Ркр из условия L= l /2 :
l
4
Pкр
0,5
2 EI min
0,5l
2
4 2 EI min
, n 2
2
l
14.
г) стержень с одним жестко закрепленным концоми другим шарнирно-опертым.
Р = Ркр
0,7l
При
потере
устойчивости
верхняя часть стержня на длине
0,7l изогнется на полуволну
синусоиды.
Определим Ркр из условия L= 0,7l :
l
Pкр
0, 7
2 EI min
0, 7l
2
2, 041 2 EI min
n 1, 423
,
l2
Вывод: чем меньше μ, тем сложнее
вывести стержень из состояния
устойчивого равновесия.
15.
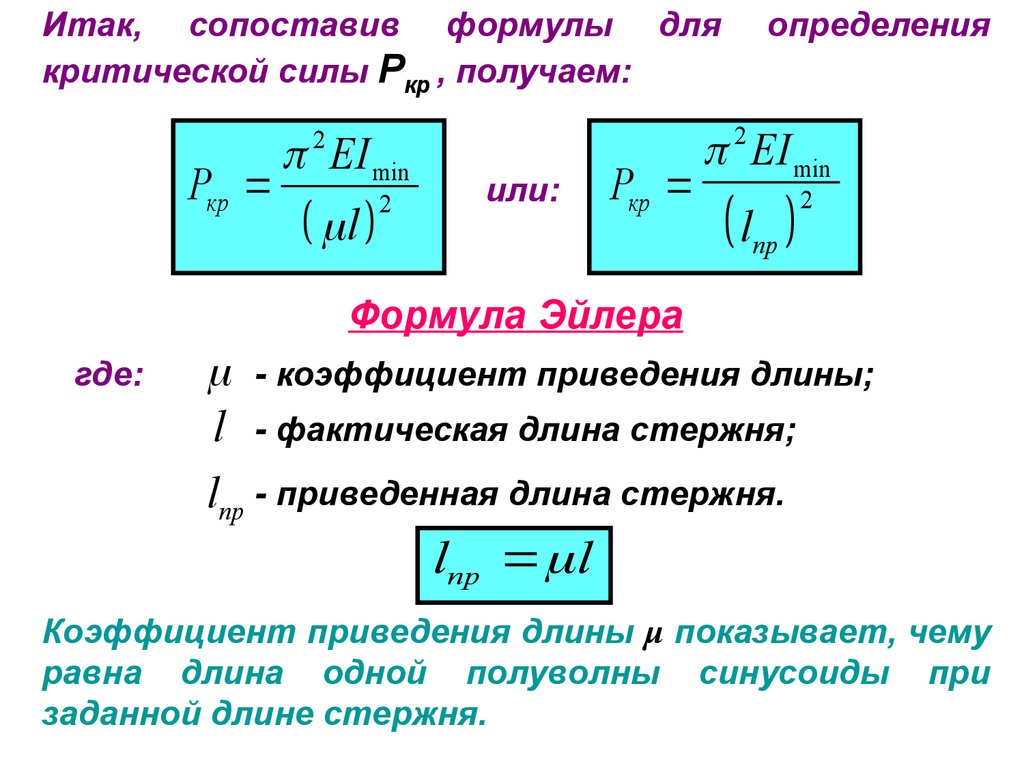
Итак, сопоставив формулы длякритической силы Ркр , получаем:
2
EI min
Pкр
2
l
или:
Pкр
определения
2 EI min
l
2
пр
Формула Эйлера
где:
- коэффициент приведения длины;
l - фактическая длина стержня;
lпр - приведенная длина стержня.
lпр l
Коэффициент приведения длины μ показывает, чему
равна длина одной полуволны синусоиды при
заданной длине стержня.
16.
Критическое напряжение.Пределы применимости формулы Эйлера.
По значению критической силы Ркр можно определить
вызываемое ею критическое сжимающее напряжение
кр , т.е. то напряжение, при котором стержень
теряет устойчивость:
кр
Ркр
2 EI min
2
F l F
Т.к. минимальный радиус инерции сечения imin
то:
I min
,
F
2 Eimin 2
l
.
кр
Введем обозначение:
,
2
l
- гибкость стержня imin
(безразмерная величина).
2
Е
Тогда: кр 2 - критическое напряжение.
17.
Формула Эйлера была получена в предположении, чтостержень деформируется в пределах действия закона
Гука, т.е.: кр пц или:
2
Е
кр 2 пц
2
Е
Определим отсюда предельную гибкость: пр
пц
Е - предельная гибкость,
или:
пр
при которой применима ф.
пц Эйлера.
Формула Эйлера применима для сжатого
Вывод: стержня лишь при условии, что его
расчетная гибкость не менее (больше или
равна) предельной гибкости расч пр .
Определим пр для различных
материалов:
2 1011
100
сталь: пр 3,14
6
200 10
дерево: пр 110
чугун: пр 80
18.
Предельная гибкость стержня не зависит от формыего сечения, а только от механических прочностных
пц
и деформационных Е свойств материала.
Если: пр , то критическое напряжение кр ,
определяемое по ф. Эйлера, оказывается выше пц
и даже выше Т и В , что противоречит логике.
Пример: Расчетная гибкость стального стержня расч
т.е. расч пр , но критическое напряжение
l
50,
imin
2 Е 3,142 2 1011
кр 2
788,8МПа , т.е. кр пц .
2
50
Значит формула Эйлера в этом случае не применима.
Если: расч пр , критическое напряжение определяют
Ф.С.Ясинский в 1892-1894гг.
по формуле Ясинского: кр а b
исследовал
вопросы
сжатый
где: а, b - коэффициенты, зависящие от устойчивости
свойств материала и определяемые
экспериментально.
стержней и получил
формулу (Россия).
эту
19.
Пример:Сталь Ст3: а 310МПа, b 1,14 МПа.
Формула
Ясинского
применима
для
стержней
малоуглеродистых сталей , у которых расч 40 100.
из
При расч 0 40 напряжение кр T const.
Установлено Е. Ламарлем в 1845г. (Бельгия).
кр
T 240
Существует зависимость между
прямая
Ламарля
кр
и пр .
прямая Ясинского
гипербола
Эйлера
пц 200
160
120
80
40
0
стержни
малой
гибкости
стержни
средней
гибкости
0 40
40 100
кр T
кр а b
20
40
60
80
стержни
большой
гибкости
100
2Е
кр 2
100
120
140
расч
20.
Стержни малой гибкости рассчитывают на прочность.Стержни большой и средней гибкости рассчитывают
на прочность и устойчивость.
Расчет сжатых стержней на
устойчивость.
Для продольно сжатых стержней кроме условия
прочности
должно
выполняться
условие
устойчивости:
Р
где:
у
n у
- допускаемое
устойчивость.
F
у
напряжение
при
расчете
кр
у
n y
- коэффициент запаса устойчивости.
на
21.
n уразличен для различных материалов, зависит
от гибкости стержня.
n у nT (или nВ )
у
где:
-
коэффициент продольного изгиба
(коэффициент уменьшения основного
допускаемого напряжения).
-
справочная величина, зависящая от материала
стержня и его гибкости.
Для стали Ст3:
Условие
устойчивости:
Условие
прочности:
Р
Р
и
F
F
120
100
0, 45
80
0, 75
60
0
0,86
1
0,6

















 physics
physics








