Расчет центрально-сжатого стержня параметрического сеченияр на устойчвость в прогамме Mathcad

1.

РАСЧЕТ ЦЕНТРАЛЬНО-СЖАТОГО
СТЕРЖНЯ
ПАРАМЕТРИЧЕСКОГО СЕЧЕНИЯ
НА УСТОЙЧВОСТЬ
В ПРОГРАММЕ MathCAD

2.

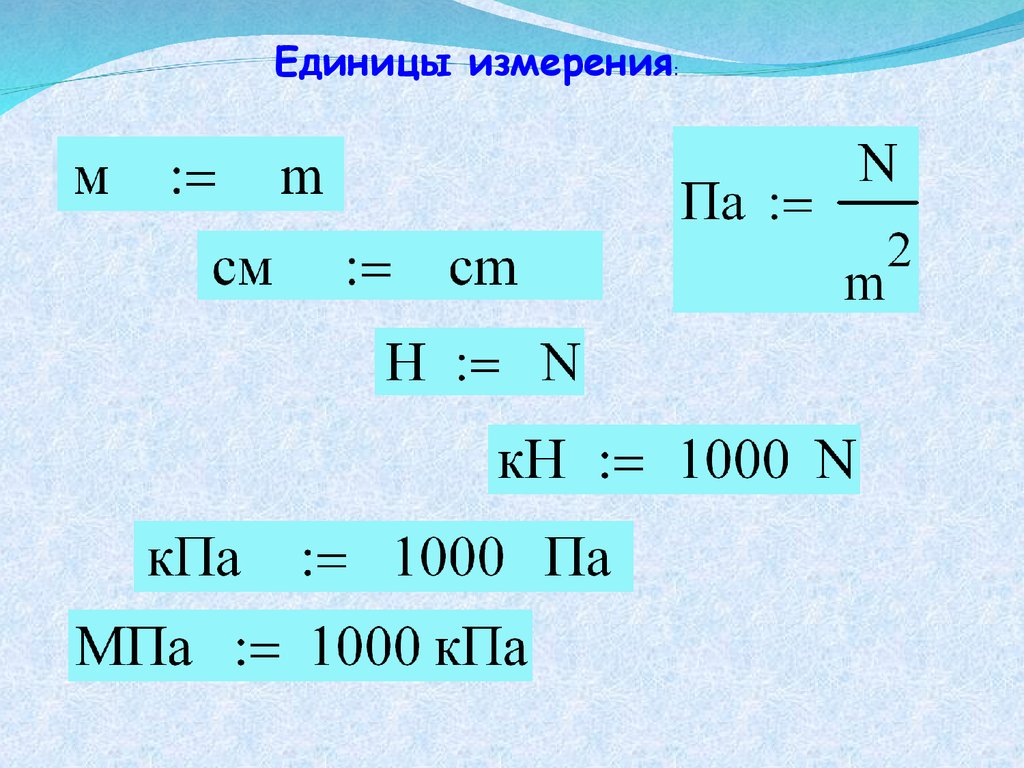
Единицы измерения
:

3.

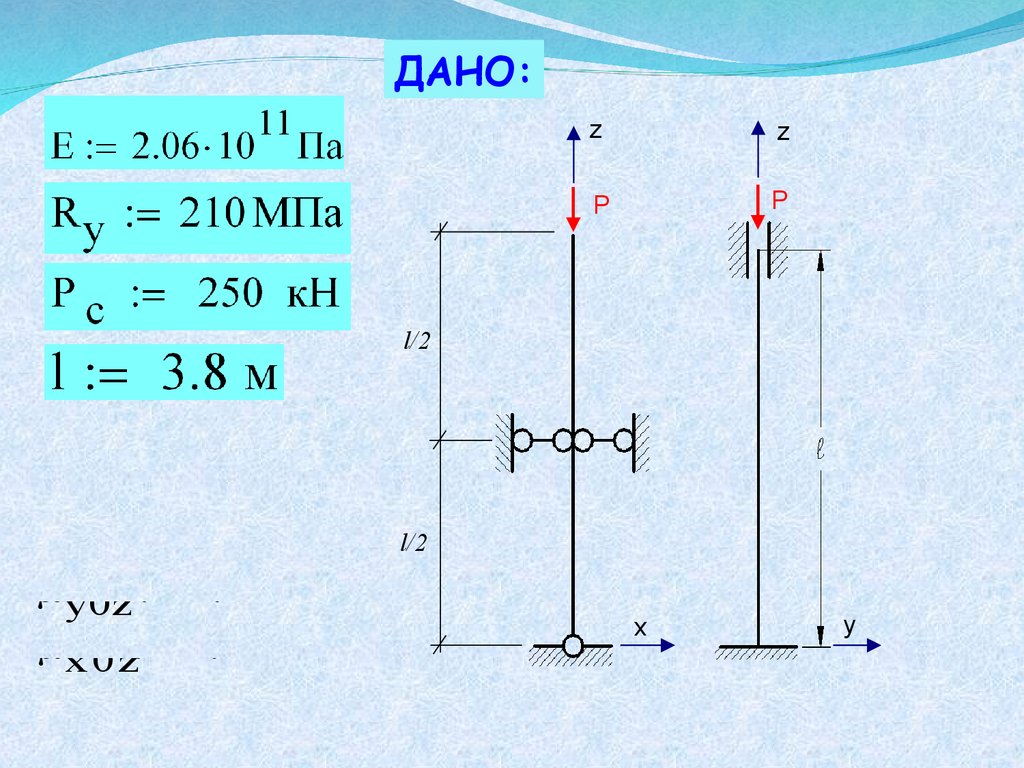
ДАНО:
z
z
P
P
l/2
l/2
y0z 0.5
x 0 z 1 .3 5
x
y

4.

5.

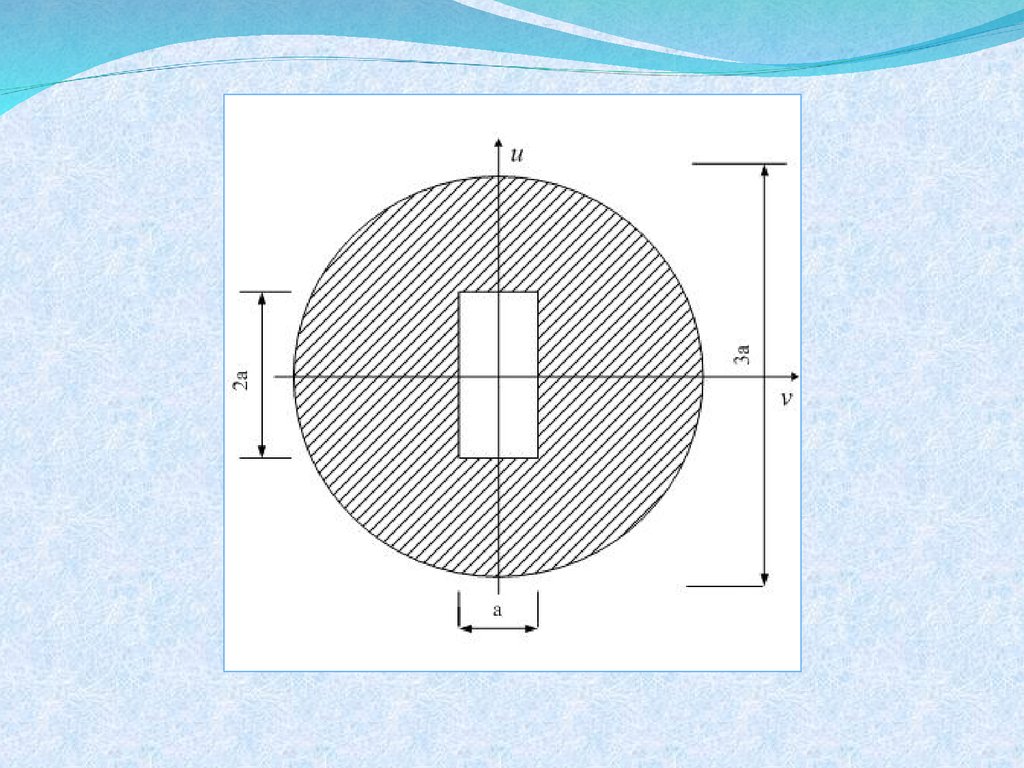
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ЗАДАННОГО СЕЧЕНИЯ
2
( 3 a)
9
F( a)
2 a a
2
2
F
(
a
)
a
2
a
4
4
Iu ( a)
Iv ( a)
( 3 a)
4
64
( 3 a)
iu ( a)
64
4
Iu ( a)
F( a)
2 a a
3
12
a ( 2a)
12
3
81
4
1 4
Iu ( a)
a a
64
6
81
4
2 4
Iv ( a)
a a
64
3
iv ( a)
Iv ( a)
F( a)

6.

КОЭФФИЦИЕНТЫ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
F( 1) 5.0686
Iu ( 1) 3.8094
iv ( 1) 0.808
Iv ( 1) 3.3094
iu ( 1) 0.8669

7.

ФОРМУЛА ПРИВЕДЕННОЙ ГИБКОСТИ
1
Ry
E
ГДЕ:
1
- ГИБКОСТЬ
-ПРИВЕДЕННАЯ ГИБКОСТЬ

8.

ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
1 if 1
φ(λ)
0
Ry
1 0.073 5.53 1 1 if 0 1 2.5
E
Ry
Ry
Ry
2
1.47 13 0.371 27.3 1 0.0275 5.53 1 if 2.5 1 4.5
E
E
E
332
if 1 4.5
2
1 51 1

9.

ОПРЕДЕЛЕНИЕ РАЦИОНАЛЬНОГО РАСПОЛОЖЕНИЯ
СЕЧЕНИЯ ДЛЯ ДВУХ ВАРИАНТОВ
1-й вариант
2-й вариант
x0z l
x0z l
2x0z
iv ( 1)
1x0z
iu ( 1)
y0z l
y0z l
1y0z
iv ( 1)
1max
2y0z
iu ( 1)
max 1x0z 1y0z
ì
1max 5.9174
2max
max 2x0z 2y0z
ì
2max 6.3487

10.

11.

12.

ВЫРАЖЕНИЕ ПАРАМЕТРА СЕЧЕНИЯ
ТРЕБУЕМУЮ ПЛОЩАДЬ И
a1 p
φ
Pc
F( 1) Ry p
max p
m
а ЧЕРЕЗ
a1 p

13.

ИТЕРАЦИИ ПРИБЛИЖЕНИЙ
НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ:
1 0.1
max( 1) 386.1132

14.

D3
1 1
2 0
j 1
while
2 1
1
0.001
j j 1
1 max 1
2 1
1
1 2
2
j 1
j 1
T
здесь -1 т.к. присваивание j+1 перед
вычислениями

15.

{5,1}
D3
{5,1}
результат - вектор-столбец из векторов-столбцов
3 D3
0
3 D3
1
a3 a1 3

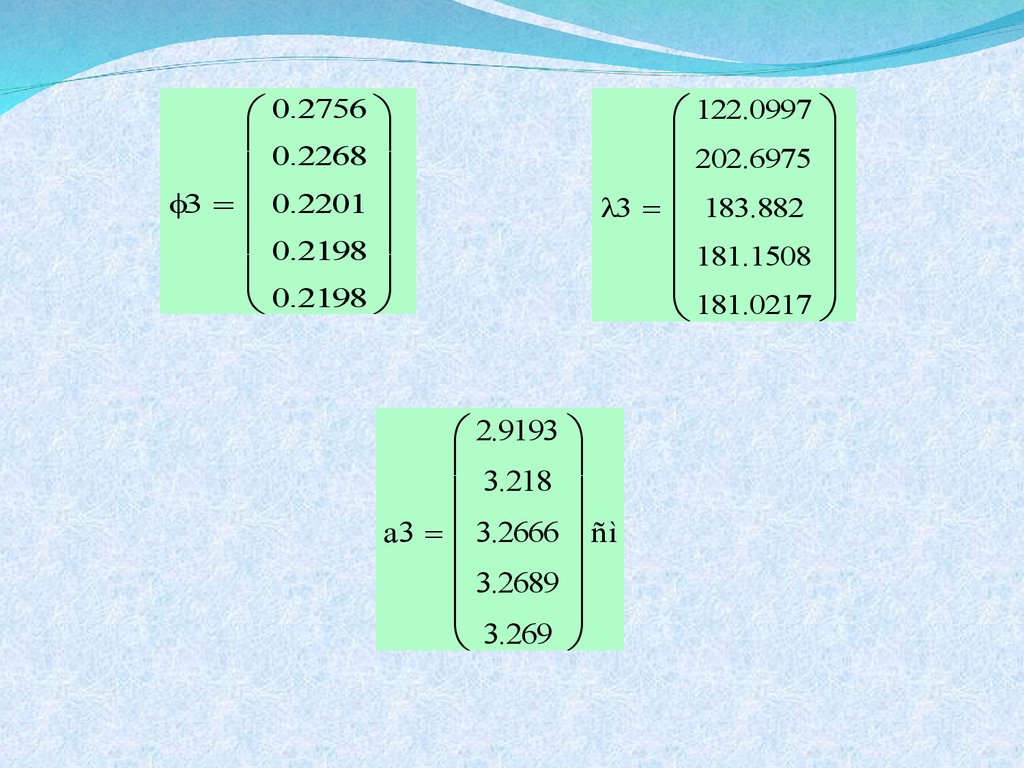
16.

0.2756
0.2268
3 0.2201
0.2198
0.2198
122.0997
202.6975
3 183.882
181.1508
181.0217
2.9193
3.218
a3 3.2666 ñì
3.2689
3.269

17.

КОЛИЧЕСТВО ИТЕРАЦИЙ:
rows ( a3) 5
РАЗМЕР ПОПЕРЕЧНОГО СЕЧЕНИЯ:

18.

КРИТИЧЕСКАЯ СИЛА:
КОЭФФИЦИЕНТ ЗАПАСА УСТОЙЧИВОСТИ