Similar presentations:
Внешние нагрузки, действующие на самолёт
1. 1. Внешние нагрузки, действующие на самолёт
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
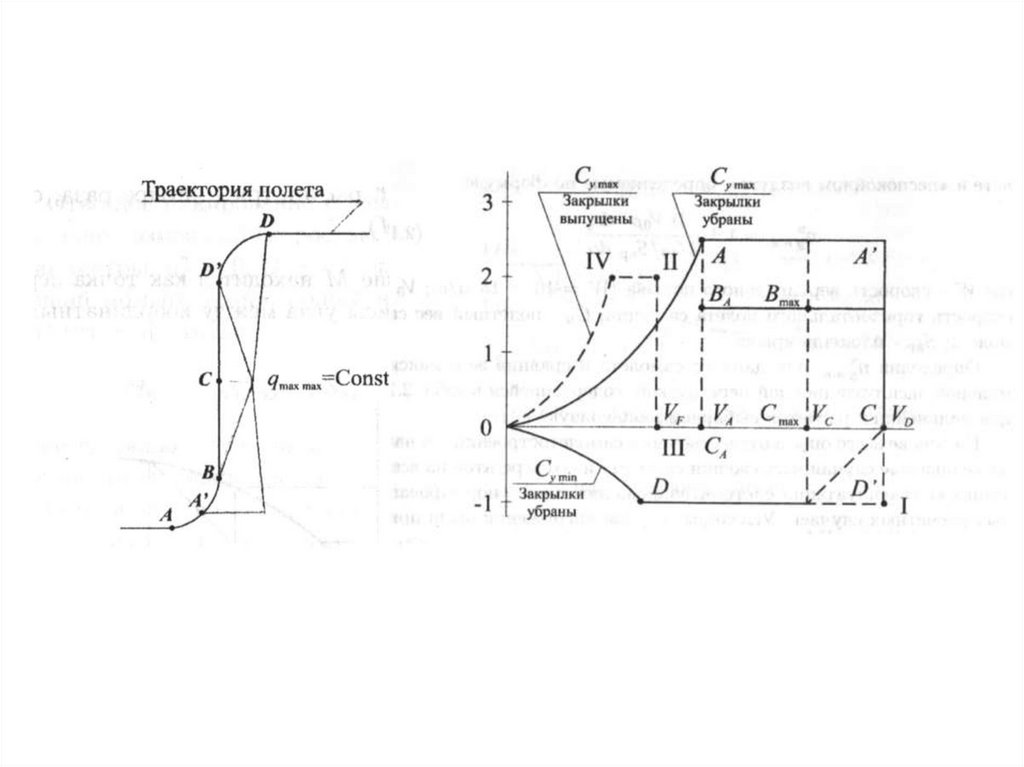
12. Равномерный прямолинейный полёт
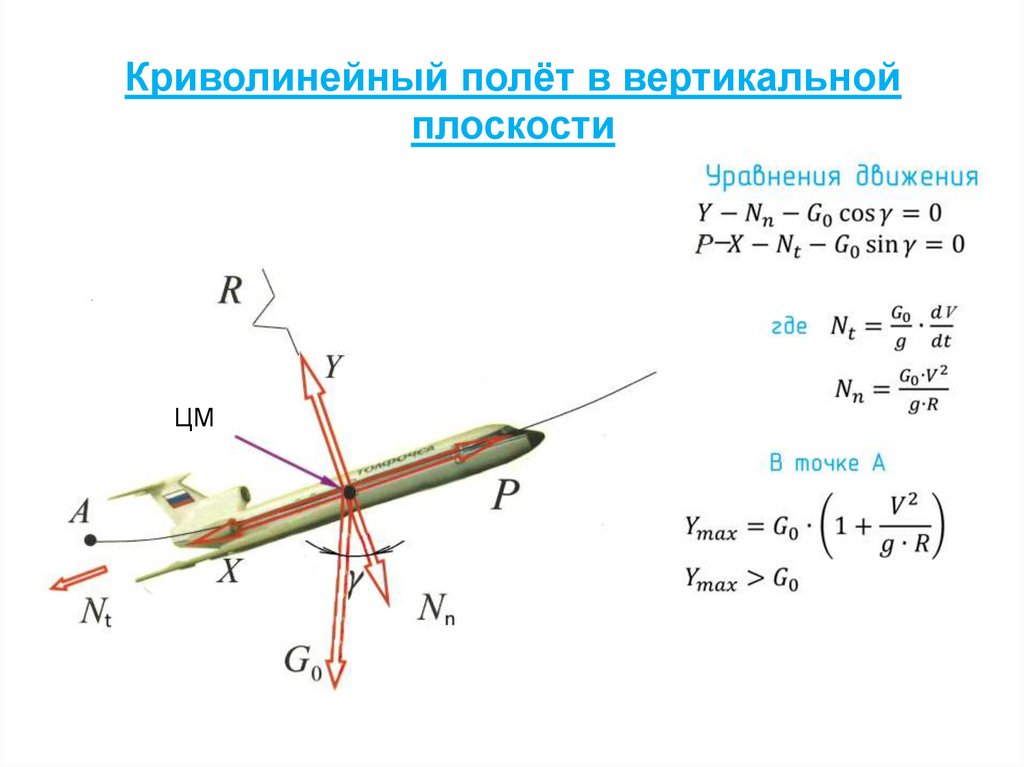
13. Криволинейный полёт в вертикальной плоскости
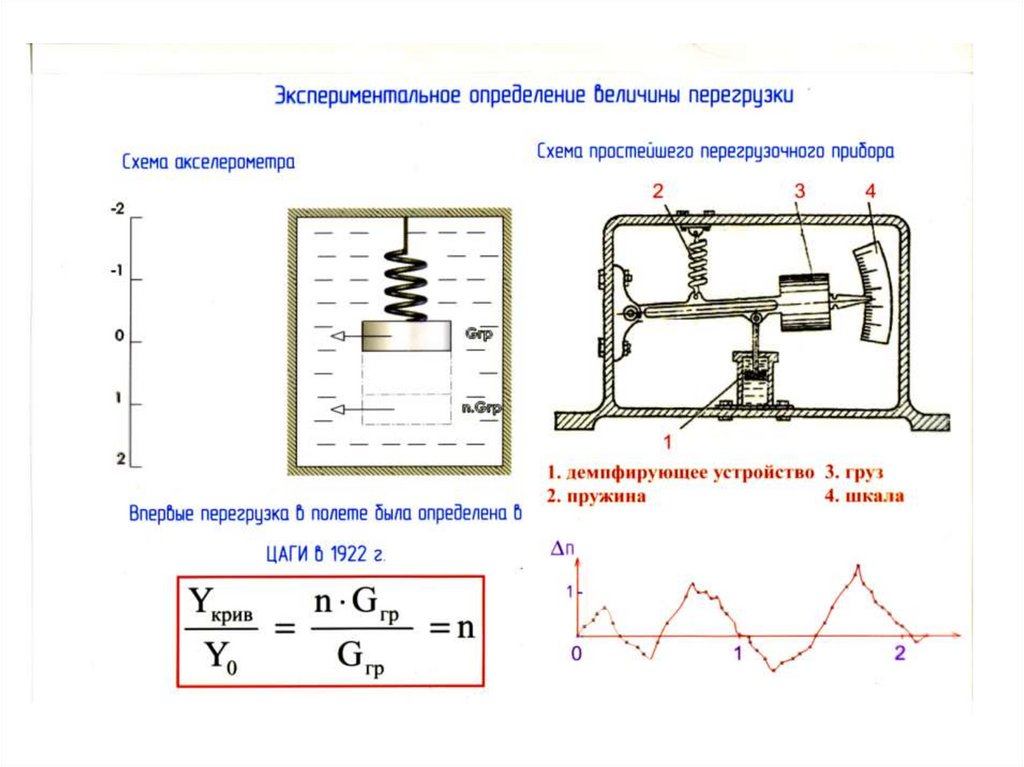
ЦМ14. Определение перегрузки
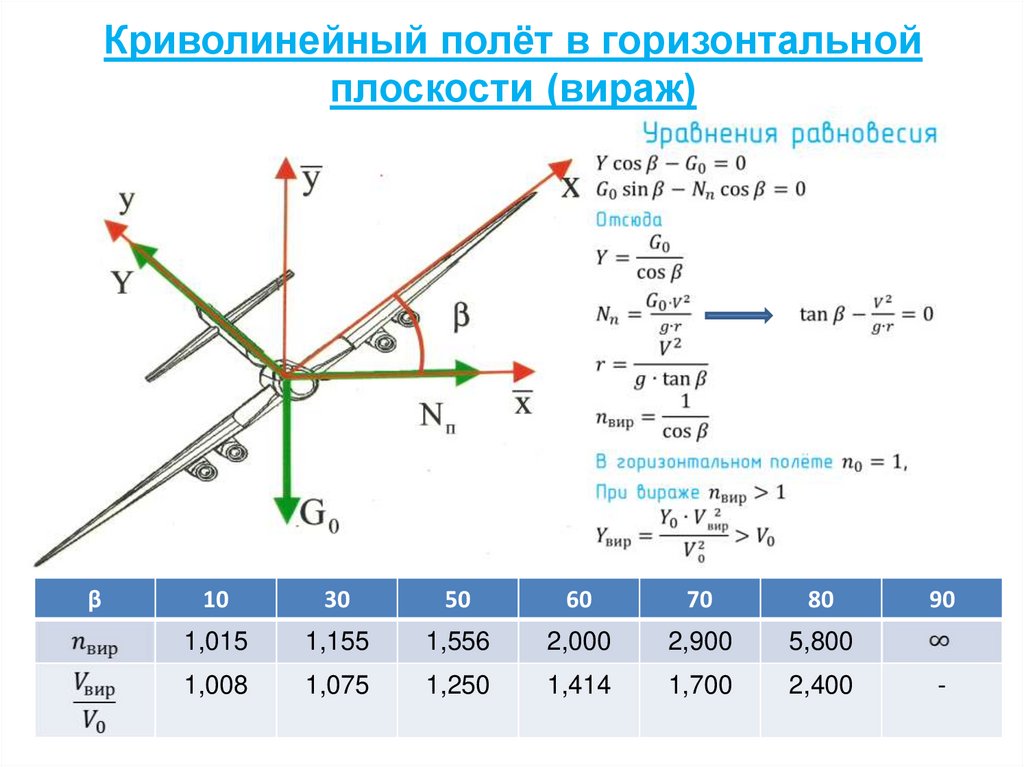
15. Криволинейный полёт в горизонтальной плоскости (вираж)
β10
30
50
60
70
80
1,015
1,155
1,556
2,000
2,900
5,800
1,008
1,075
1,250
1,414
1,700
2,400
90
-
16.
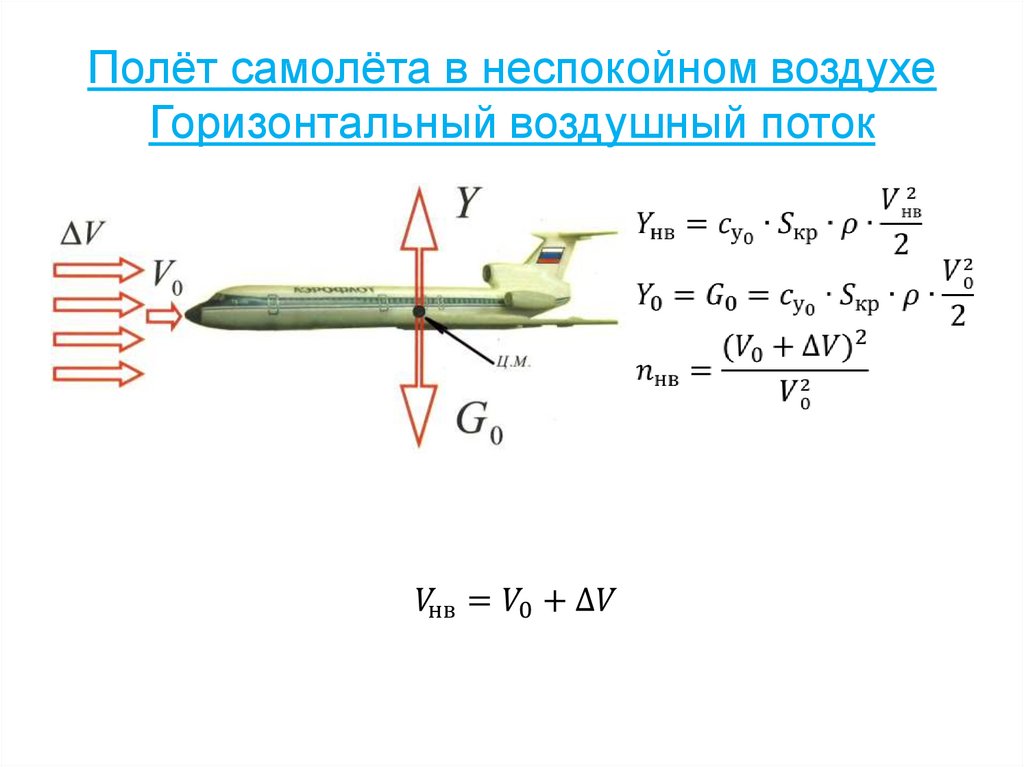
17. Полёт самолёта в неспокойном воздухе Горизонтальный воздушный поток
18. Вертикальные воздушные потоки а) Мгновенный вход крыла в вертикальный поток большой интенсивности (W>15 м/с)
Вертикальные воздушные потокиа) Мгновенный вход крыла в вертикальный поток
большой интенсивности (W>15 м/с)
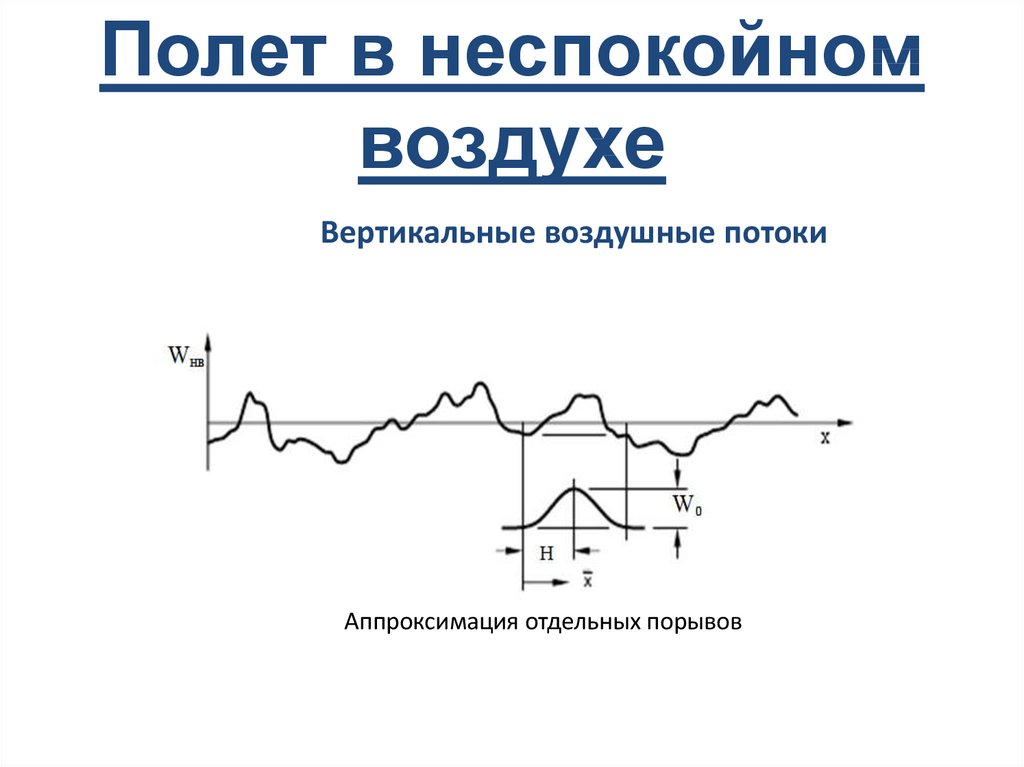
19. Полет в неспокойном воздухе
Вертикальные воздушные потокиАппроксимация отдельных порывов
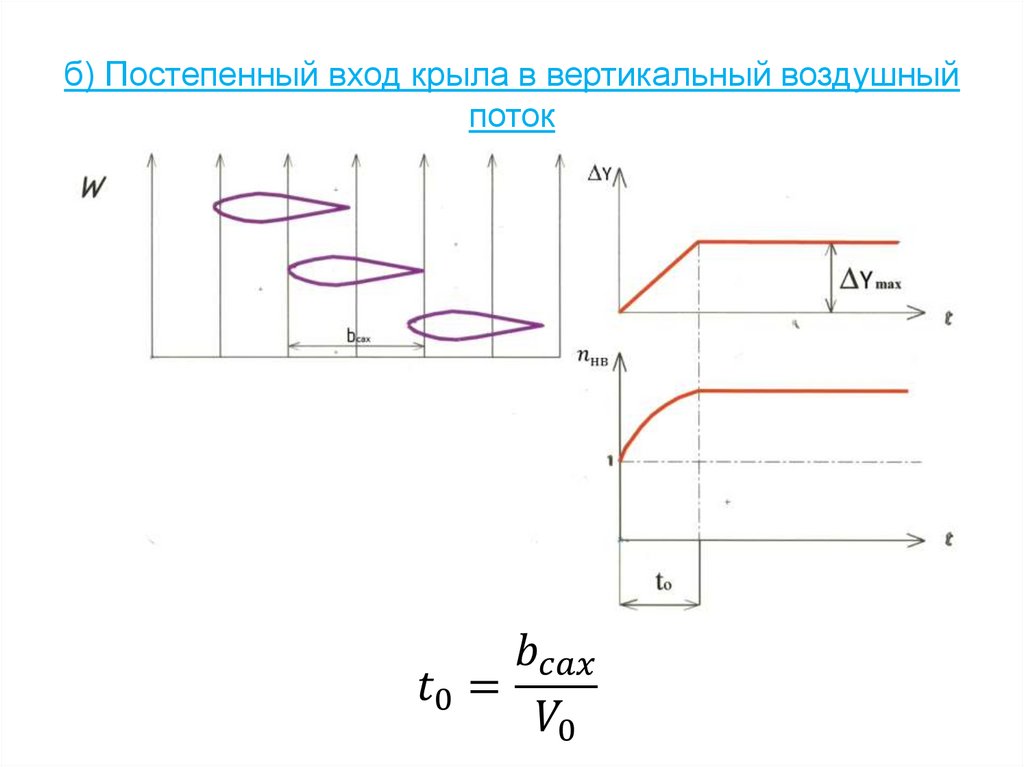
20. б) Постепенный вход крыла в вертикальный воздушный поток
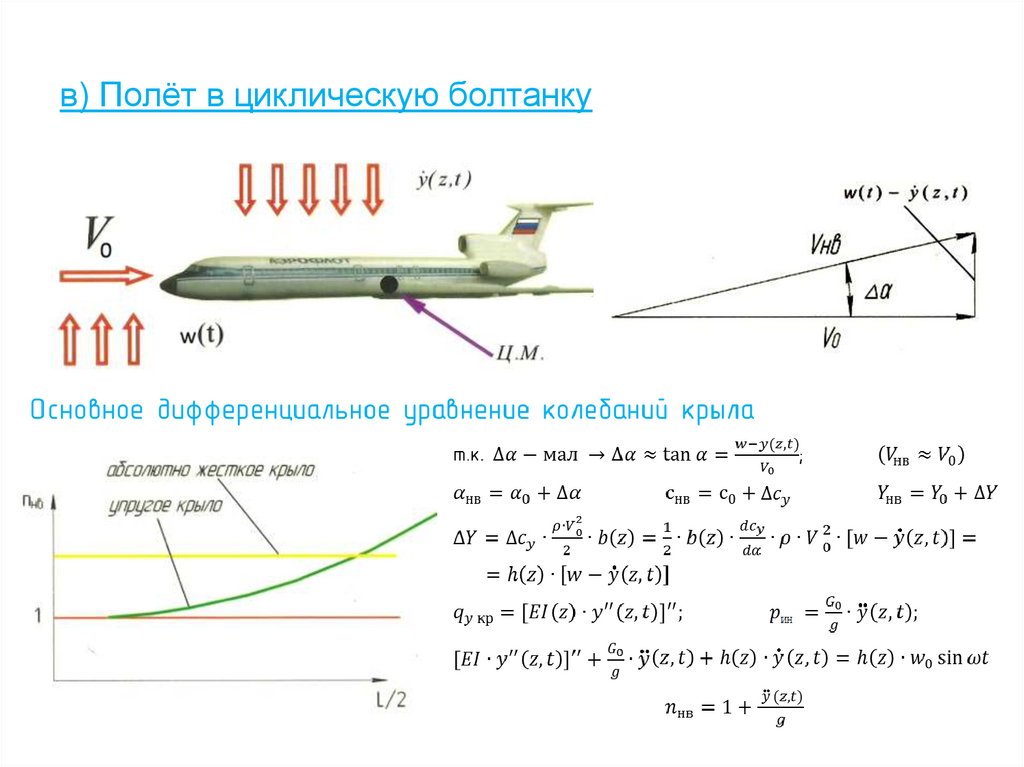
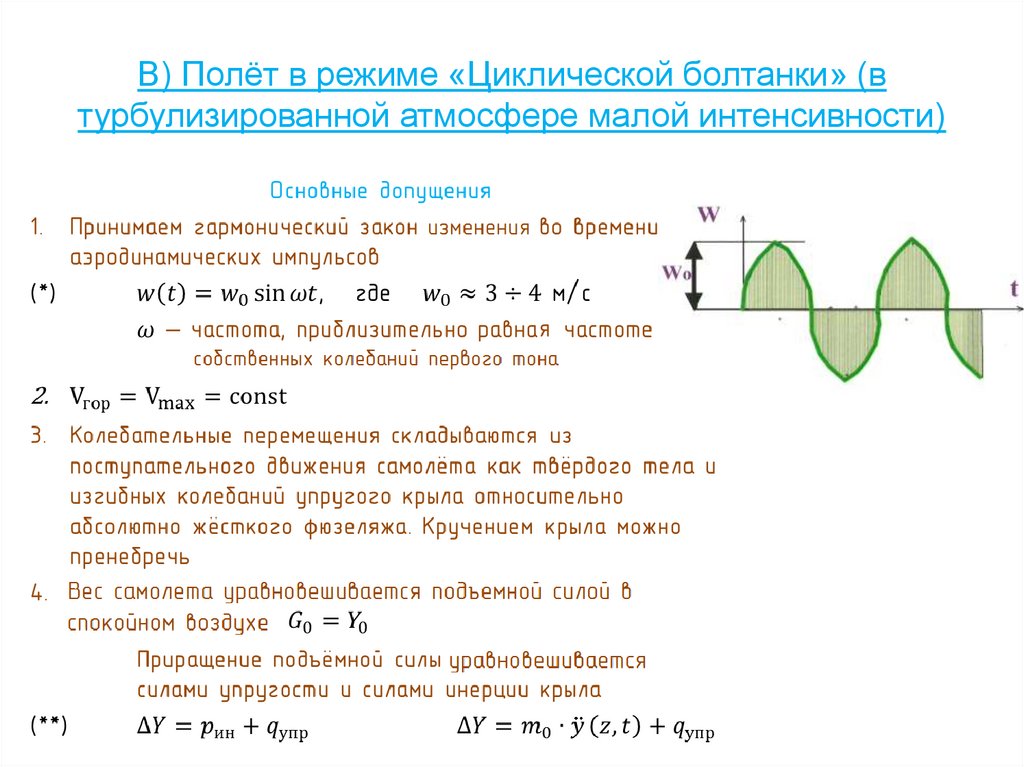
21. в) Полёт в циклическую болтанку
22. В) Полёт в режиме «Циклической болтанки» (в турбулизированной атмосфере малой интенсивности)
23. Укрупнённая классификация самолётов
NТипы самолётов
1
Лёгкие маневренные самолёты
8-9
2
Самолёты ограниченной
маневренности
4-6
3
Тяжёлые неманевренные самолёты
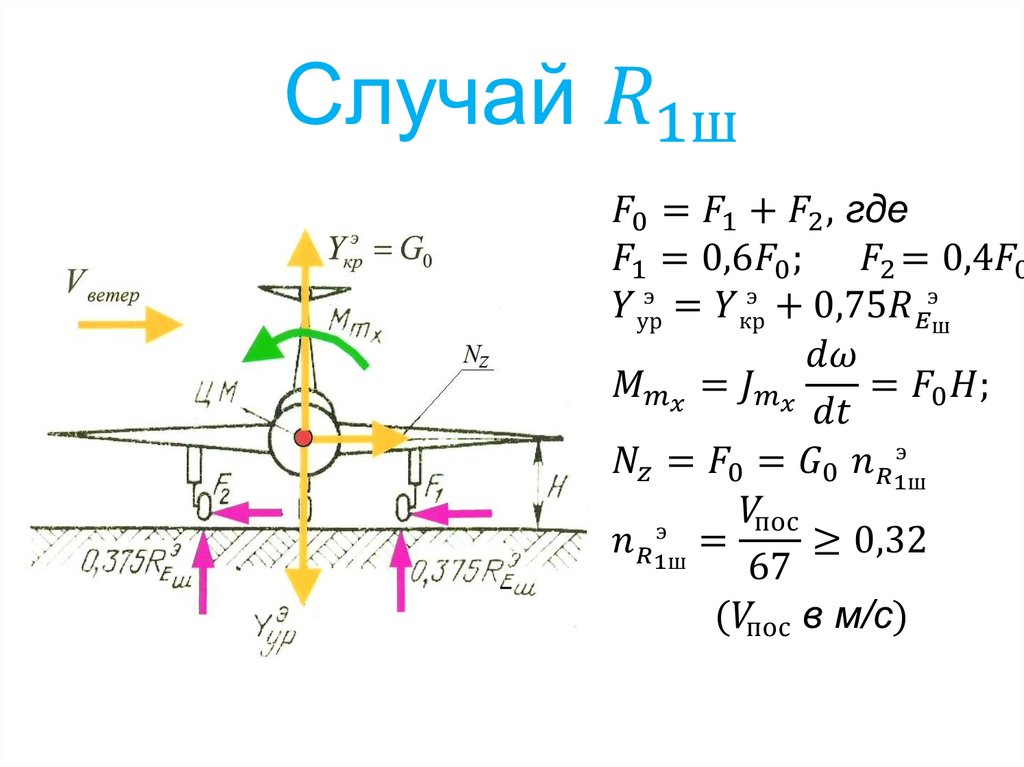
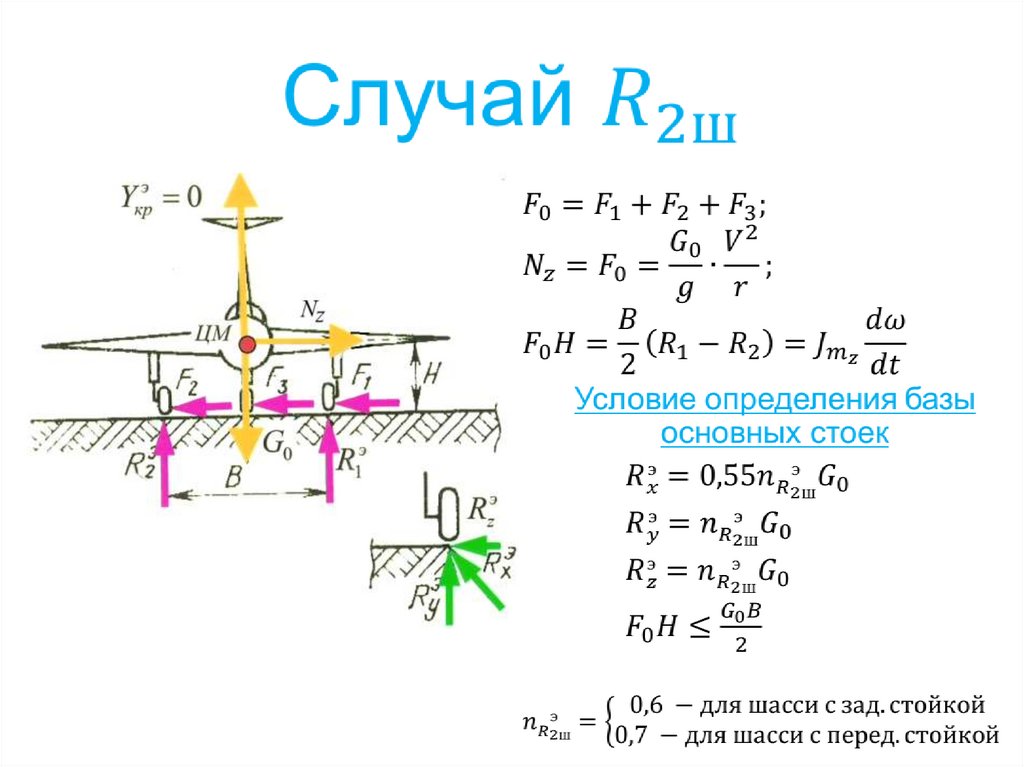
2-3
Значение перегрузок при выполнении фигур высшего
пилотажа
N
Название фигур
1
Спираль
3-4
2
Бочка
4-5
3
Боевой разворот
3-4
4
Штопор
2-3
5
Вираж
3-4
6
Многократная бочка
5-7
7
Петля Нестерова
3-6
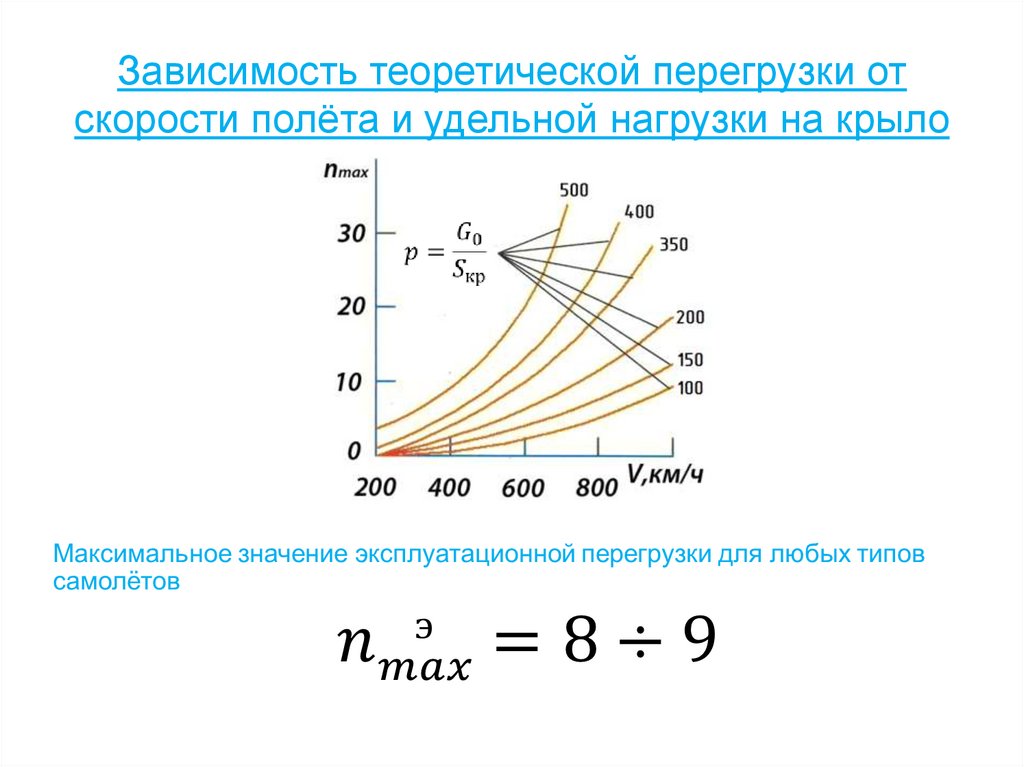
24. Зависимость теоретической перегрузки от скорости полёта и удельной нагрузки на крыло
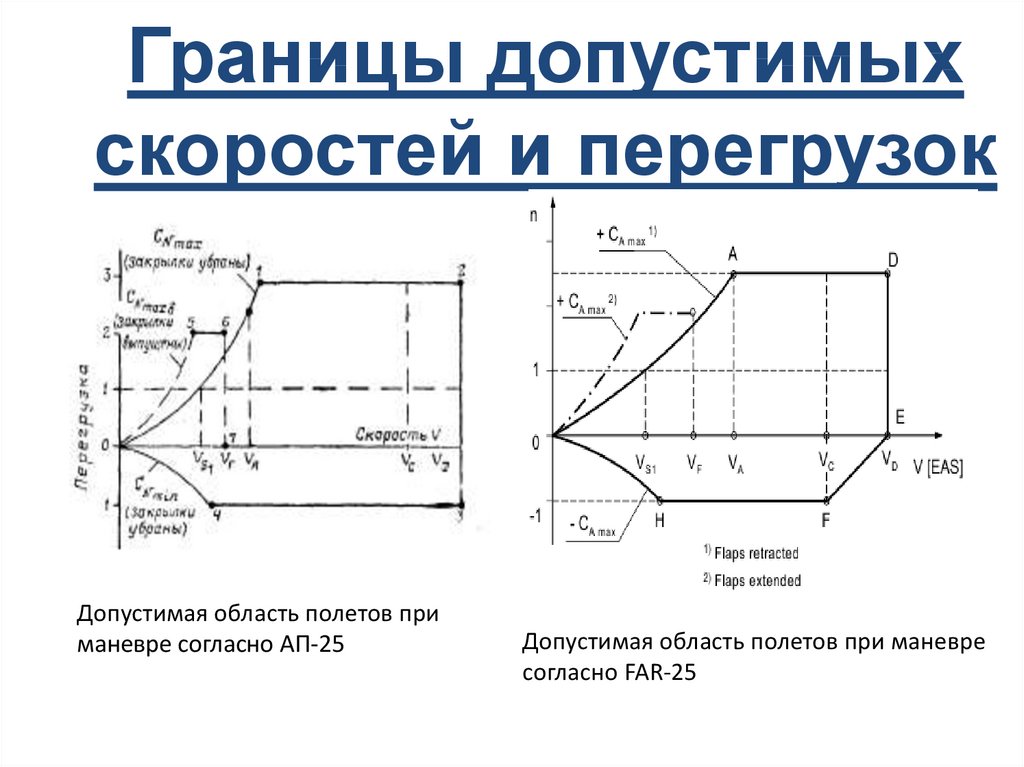
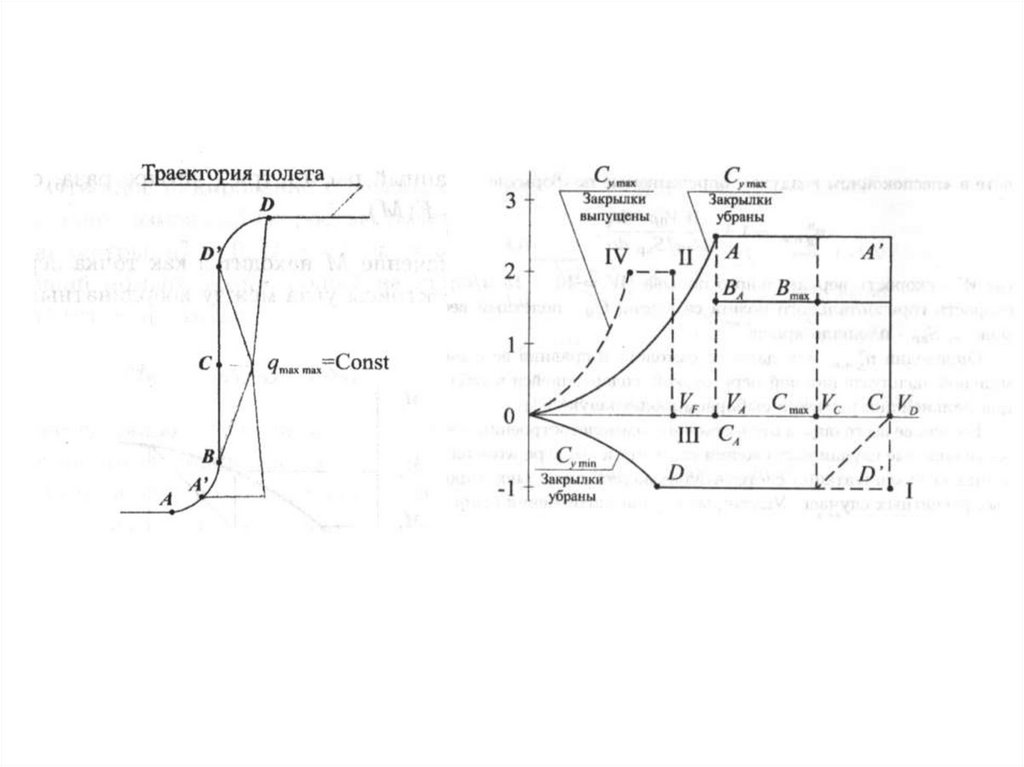
25. Границы допустимых скоростей и перегрузок
Допустимая область полетов приманевре согласно АП-25
Допустимая область полетов при маневре
согласно FAR-25
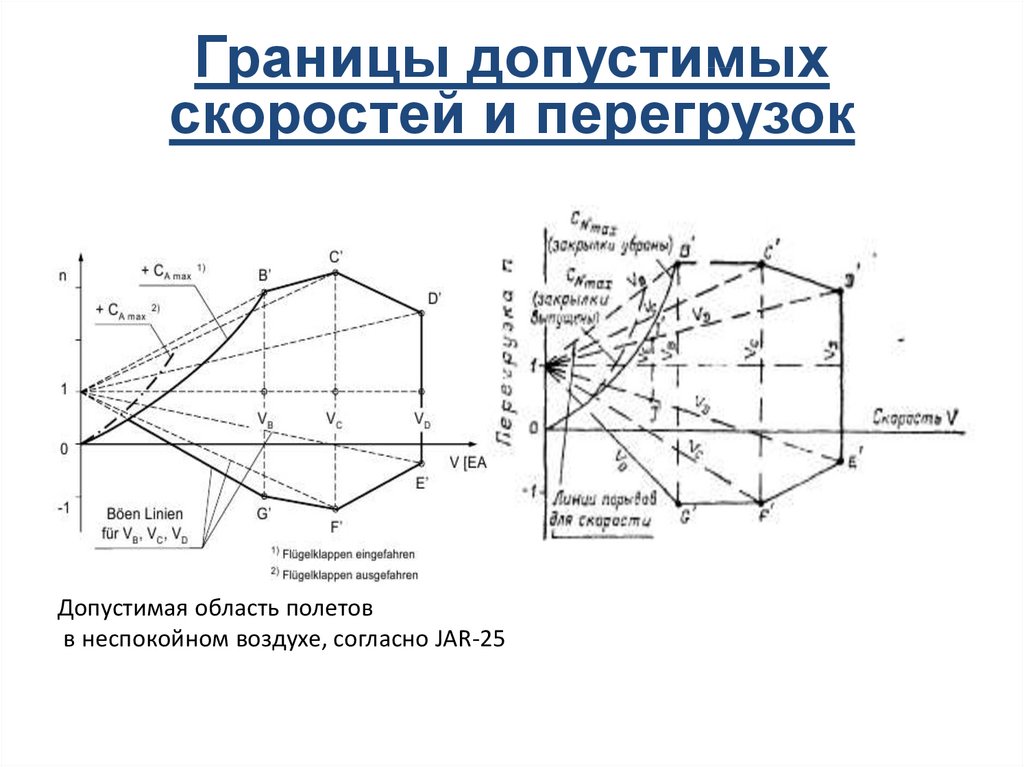
26.
Границы допустимыхскоростей и перегрузок
Допустимая область полетов
в неспокойном воздухе, согласно JAR-25
27.
Границы допустимых скоростей иперегрузок
28.
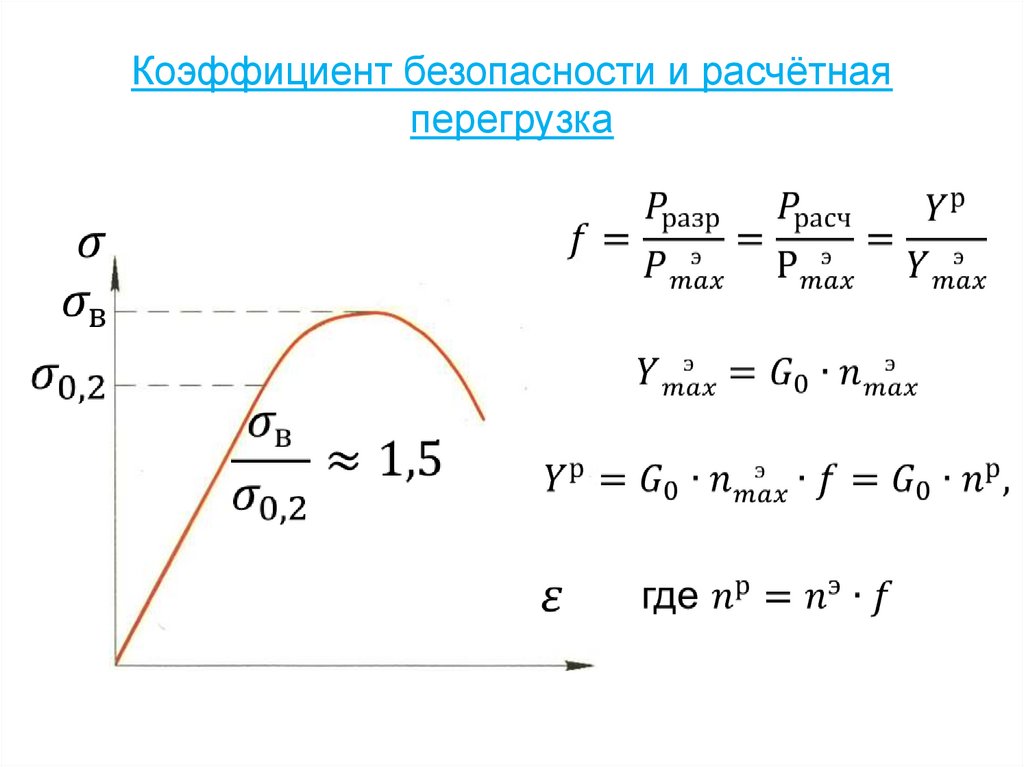
29. Коэффициент безопасности и расчётная перегрузка
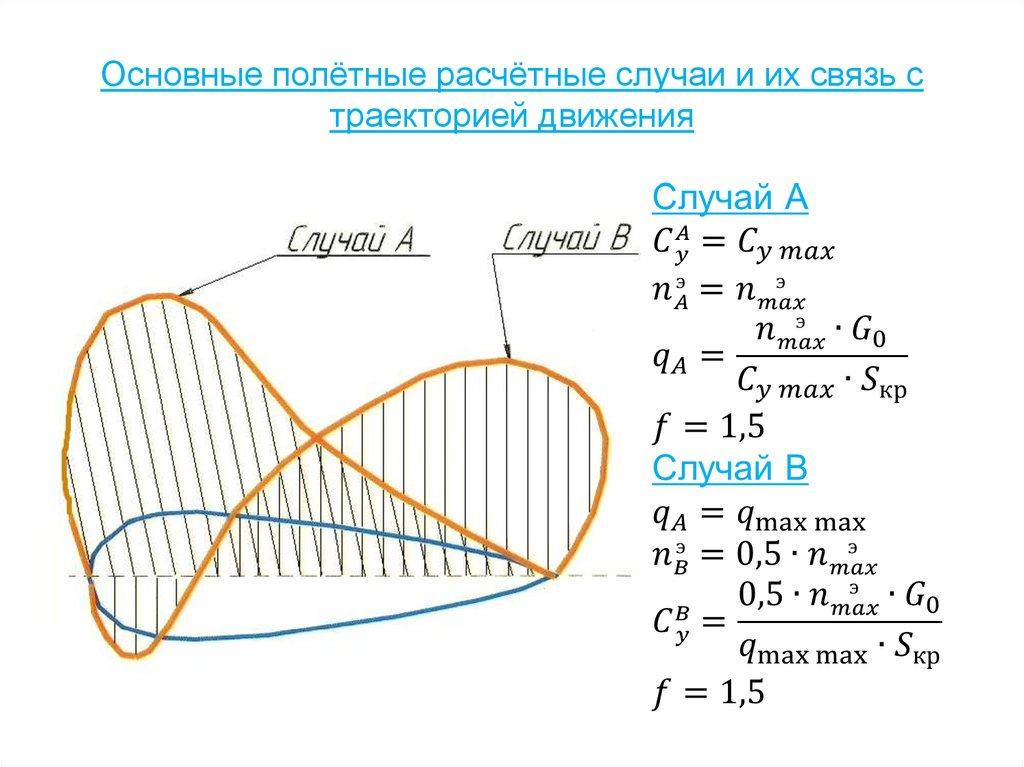
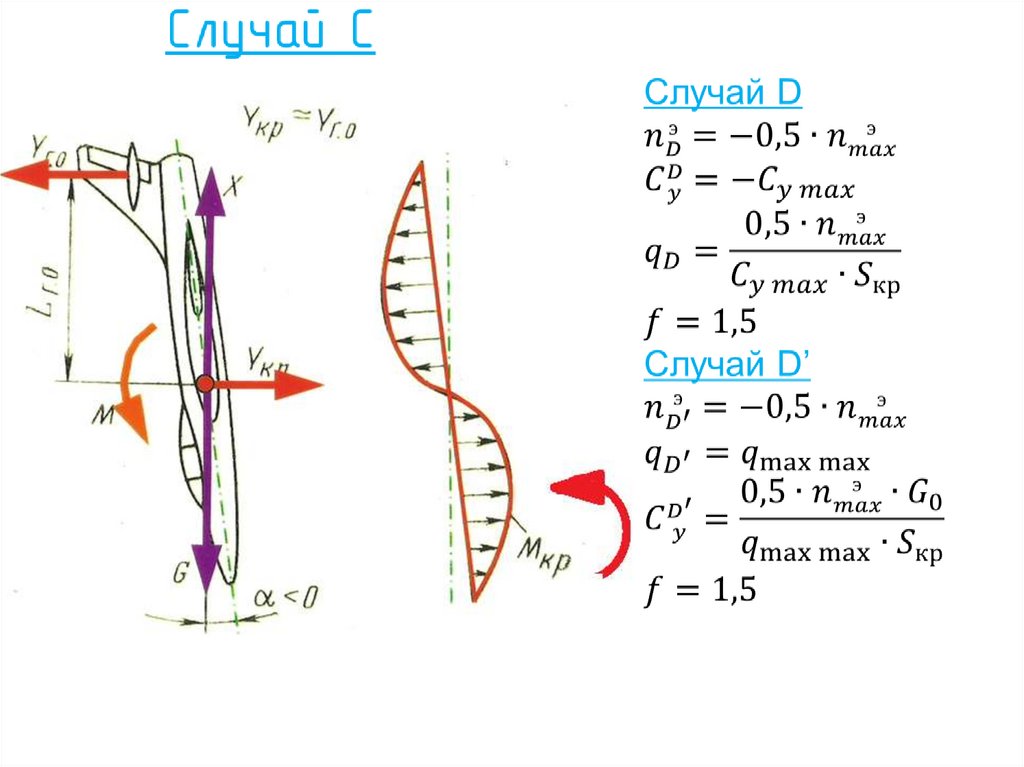
30. Основные полётные расчётные случаи и их связь с траекторией движения
31.
32.
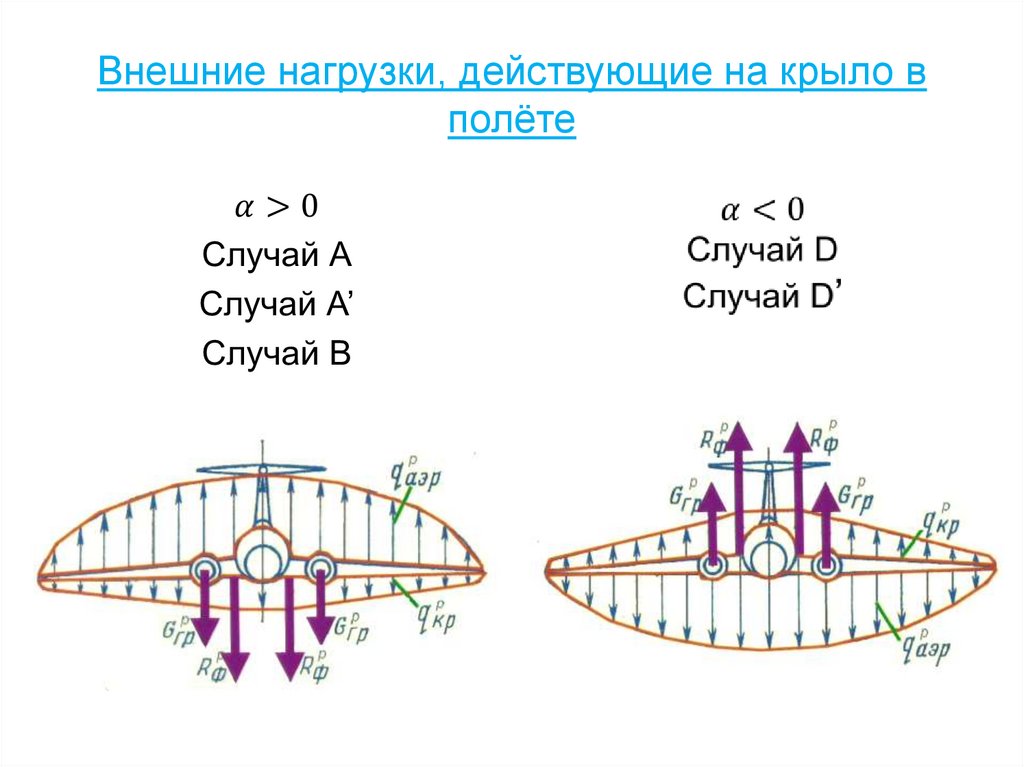
33. Внешние нагрузки, действующие на крыло в полёте
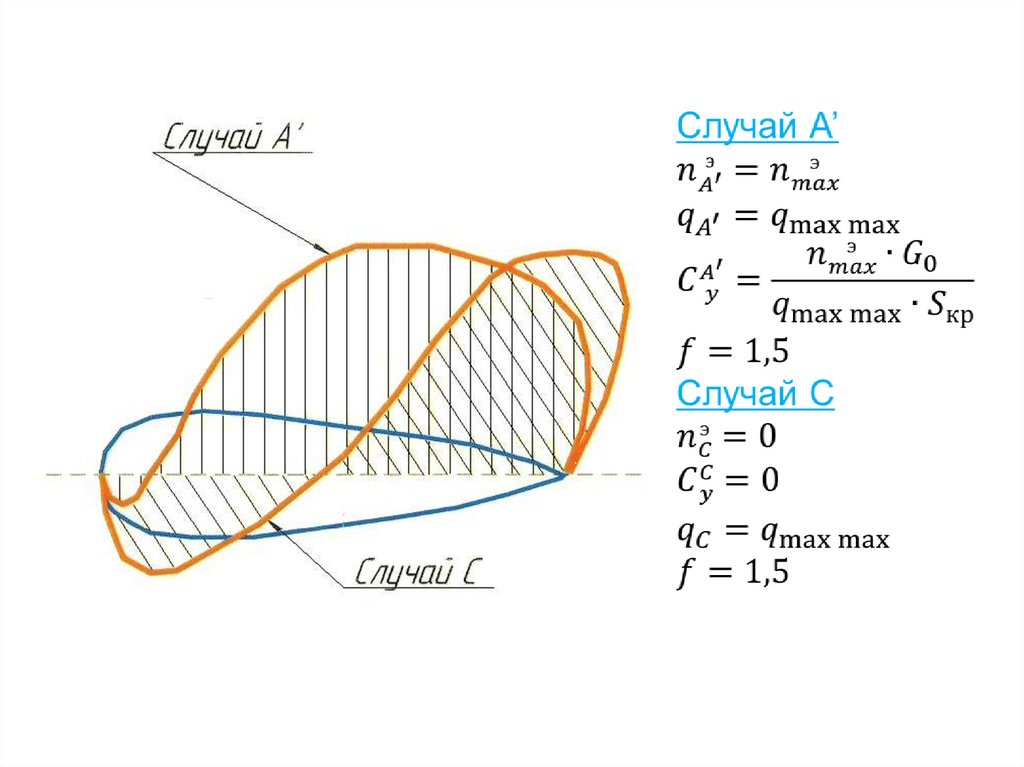
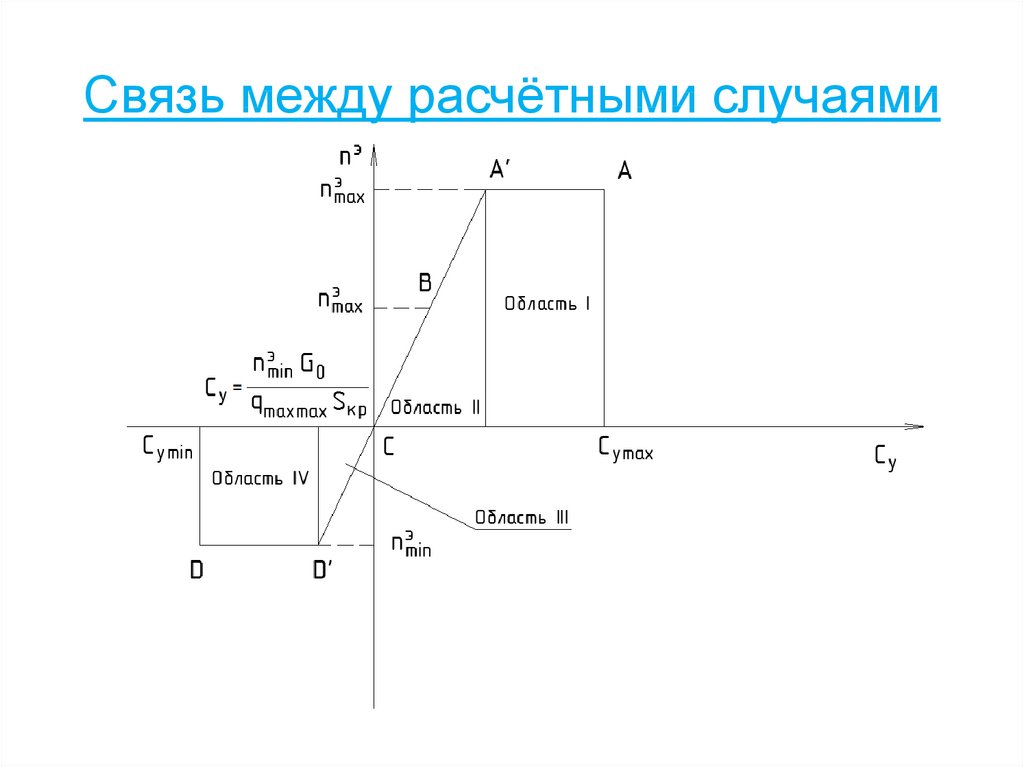
34. Связь между расчётными случаями
35. 2. Распределение внешних нагрузок по размаху крыла
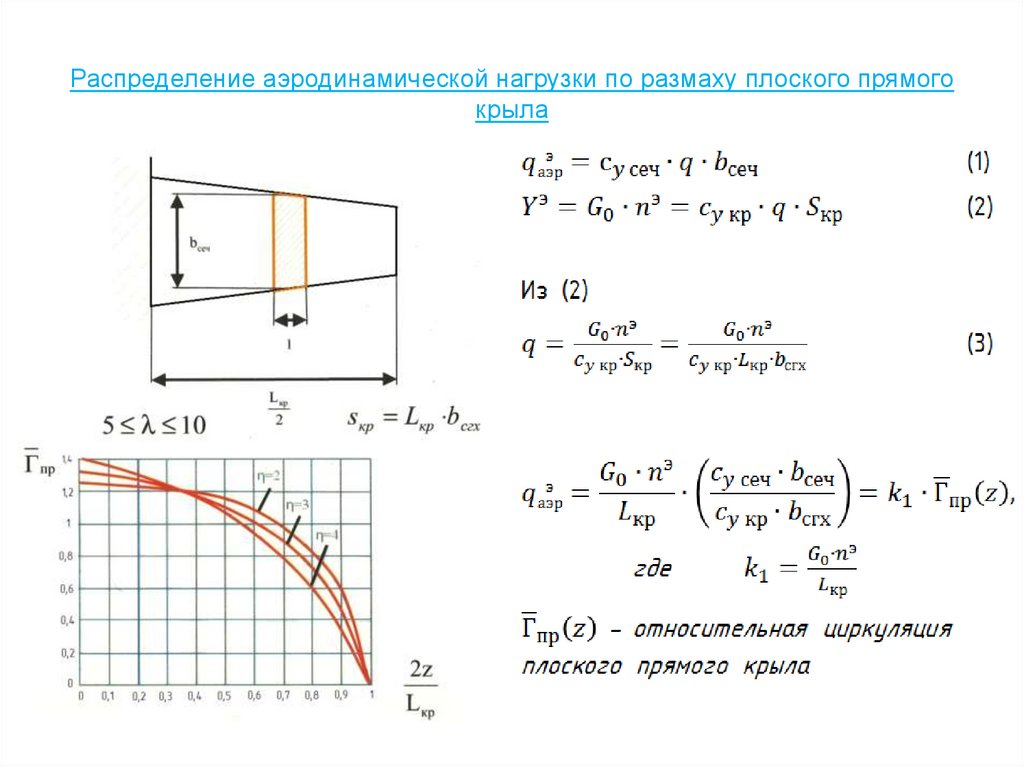
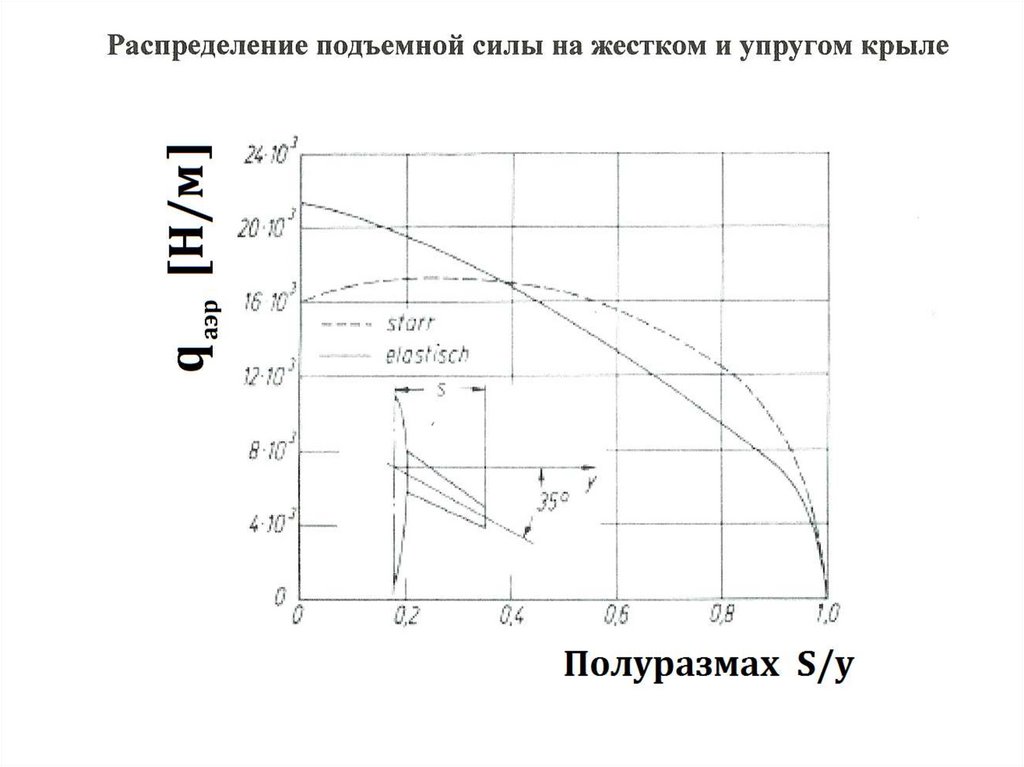
36. Распределение аэродинамической нагрузки по размаху плоского прямого крыла
37. Учёт закрутки крыла
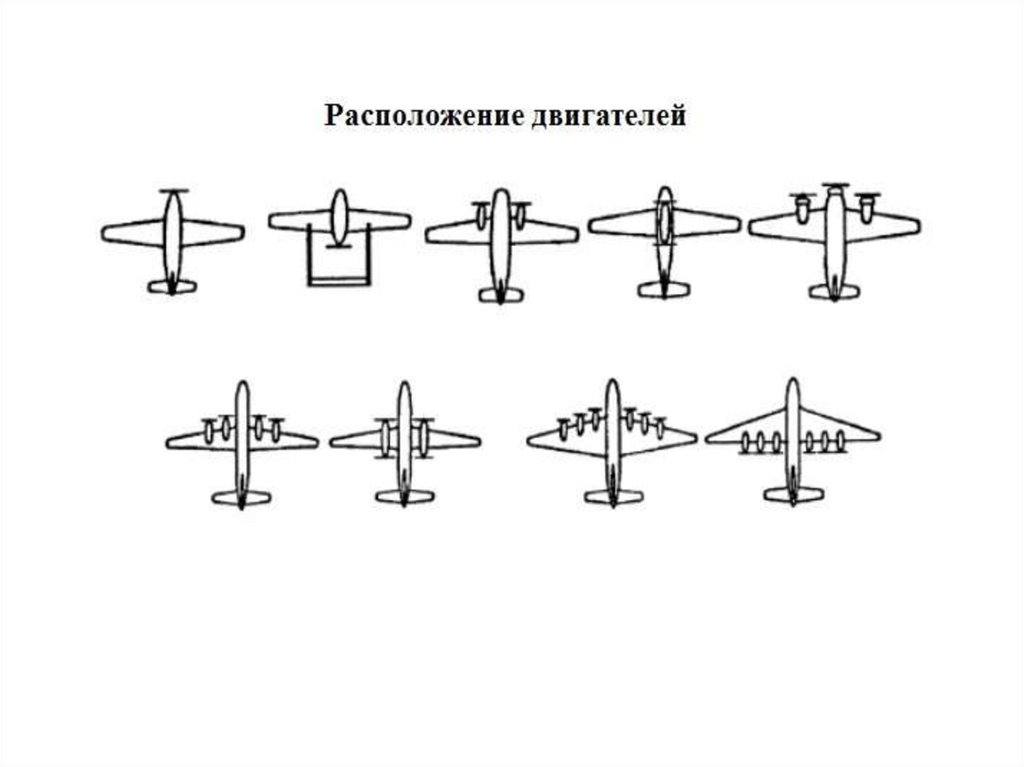
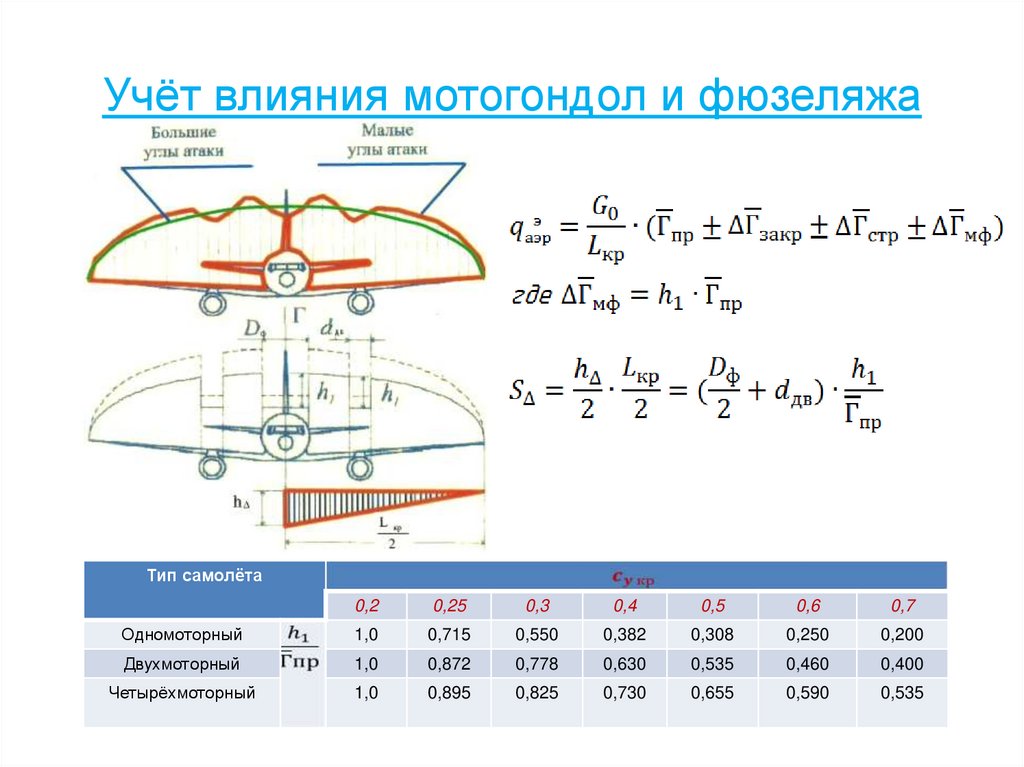
38. Учёт влияния мотогондол и фюзеляжа
Тип самолёта0,2
0,25
0,3
0,4
0,5
0,6
0,7
Одномоторный
1,0
0,715
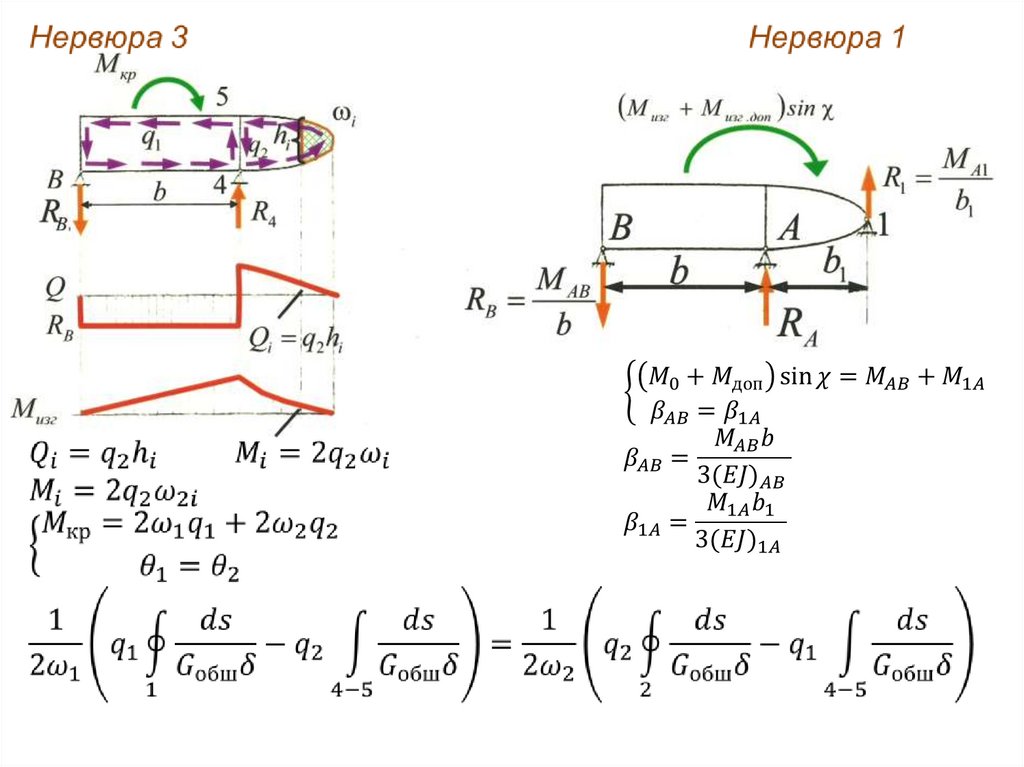
0,550
0,382
0,308
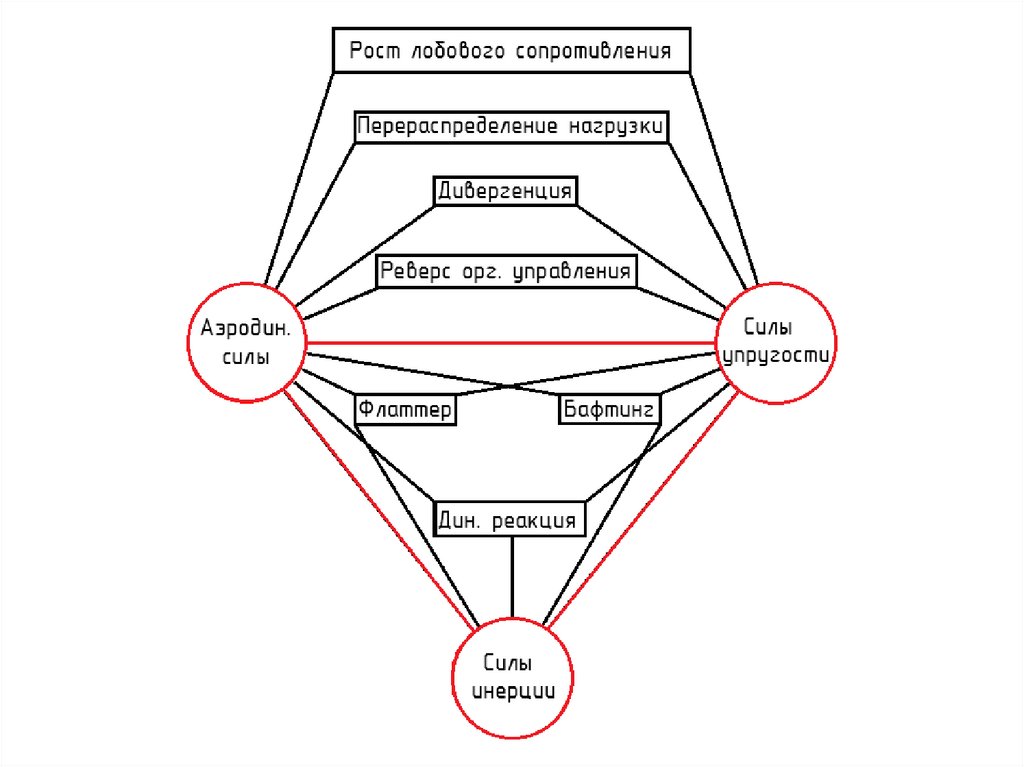
0,250
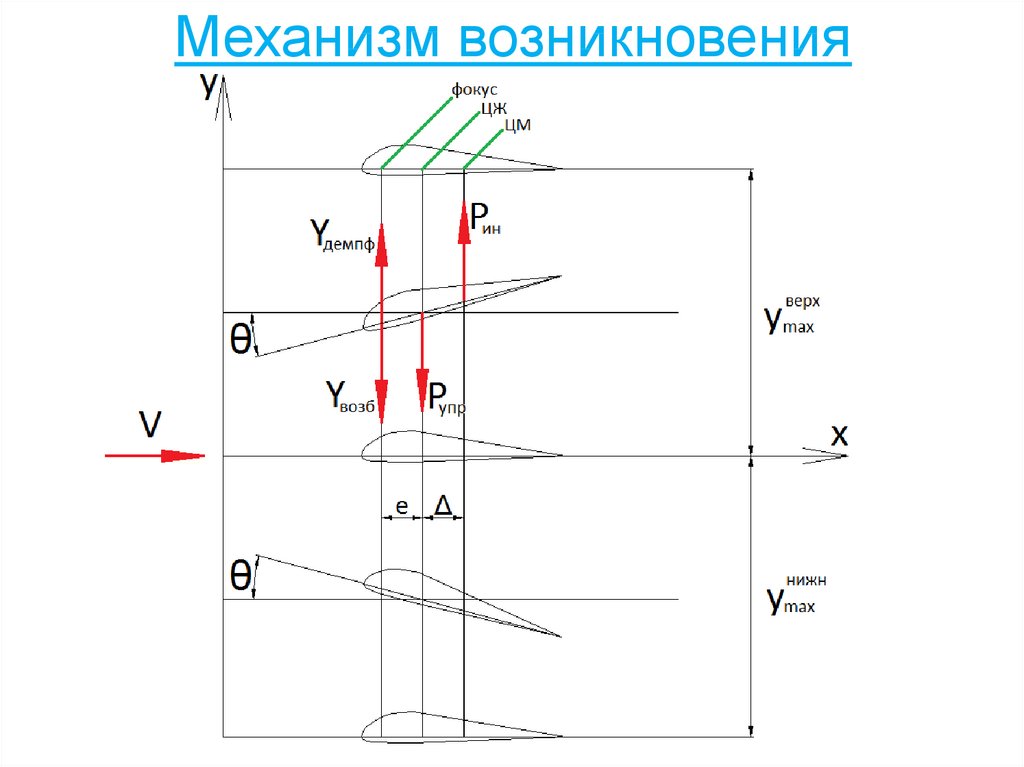
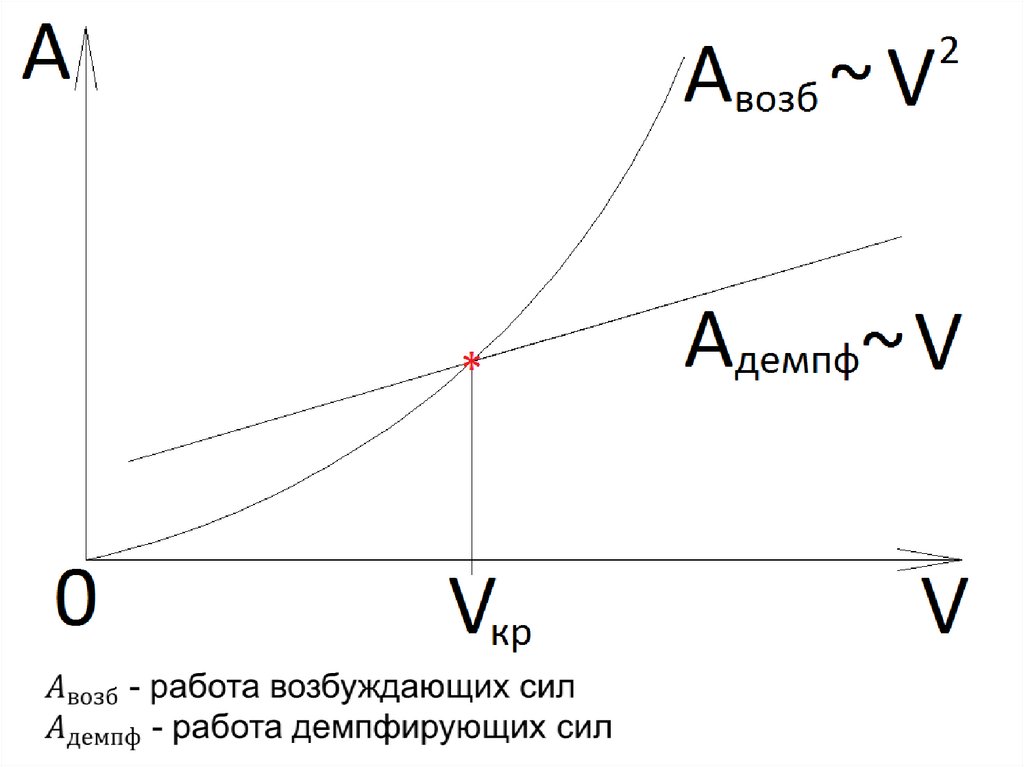
0,200
Двухмоторный
1,0
0,872
0,778
0,630
0,535
0,460
0,400
Четырёхмоторный
1,0
0,895
0,825
0,730
0,655
0,590
0,535
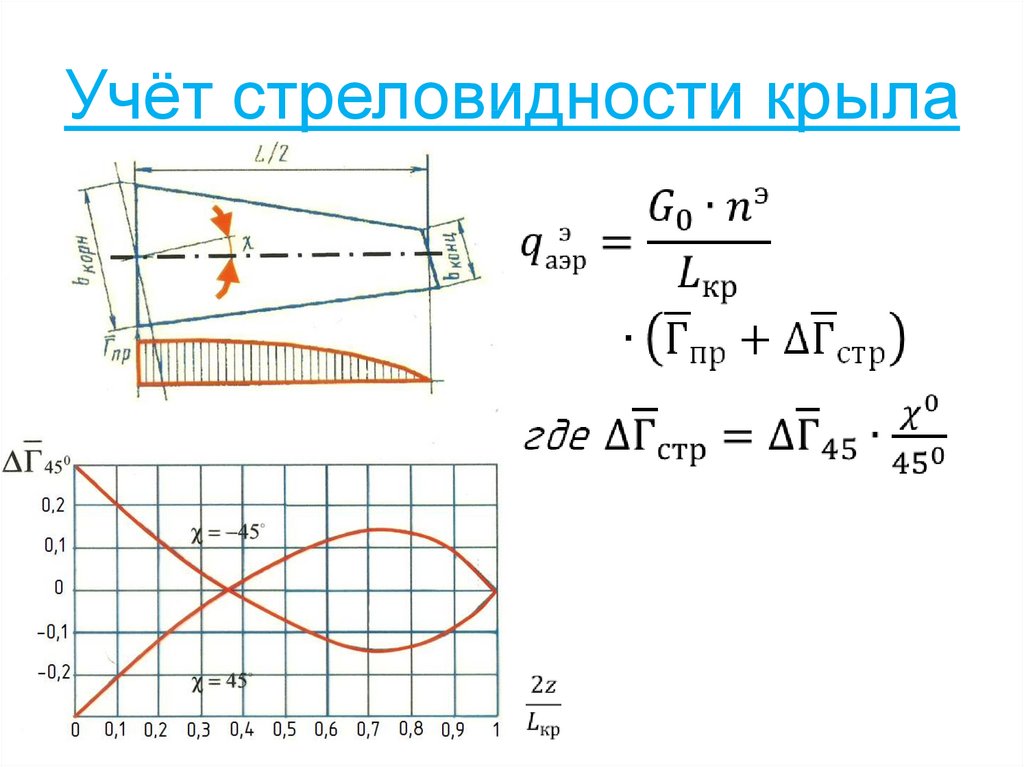
39. Учёт стреловидности крыла
40. Распределение аэродинамической нагрузки по размаху треугольного крыла
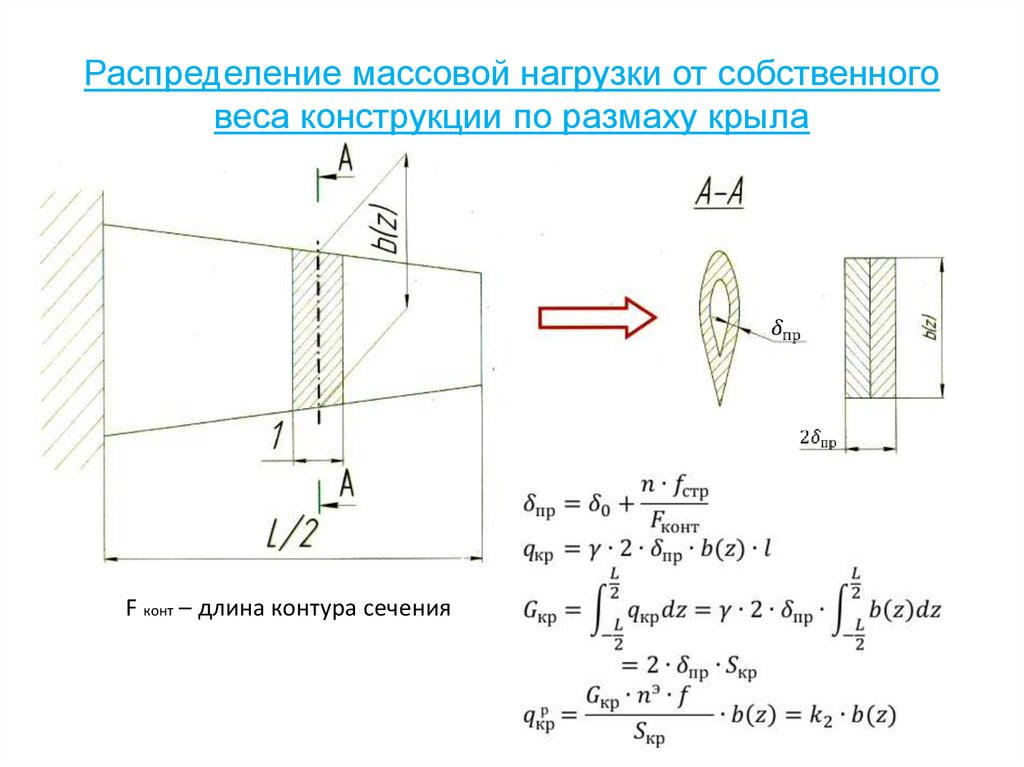
41. Распределение массовой нагрузки от собственного веса конструкции по размаху крыла
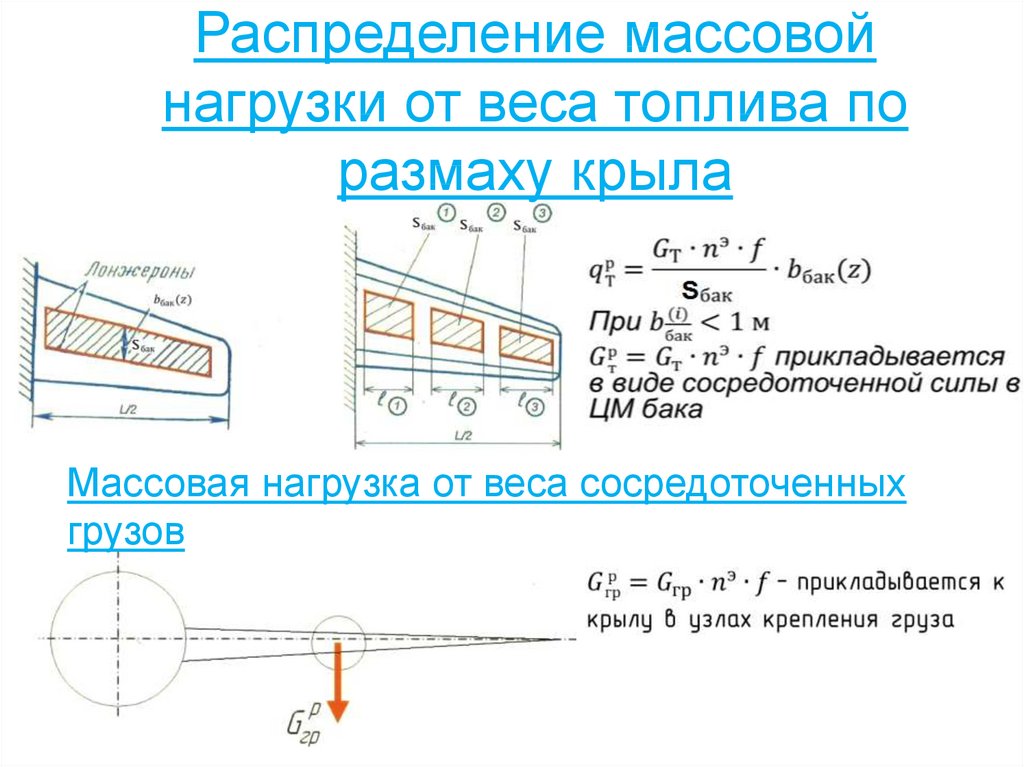
F конт – длина контура сечения42. Распределение массовой нагрузки от веса топлива по размаху крыла
Массовая нагрузка от веса сосредоточенныхгрузов
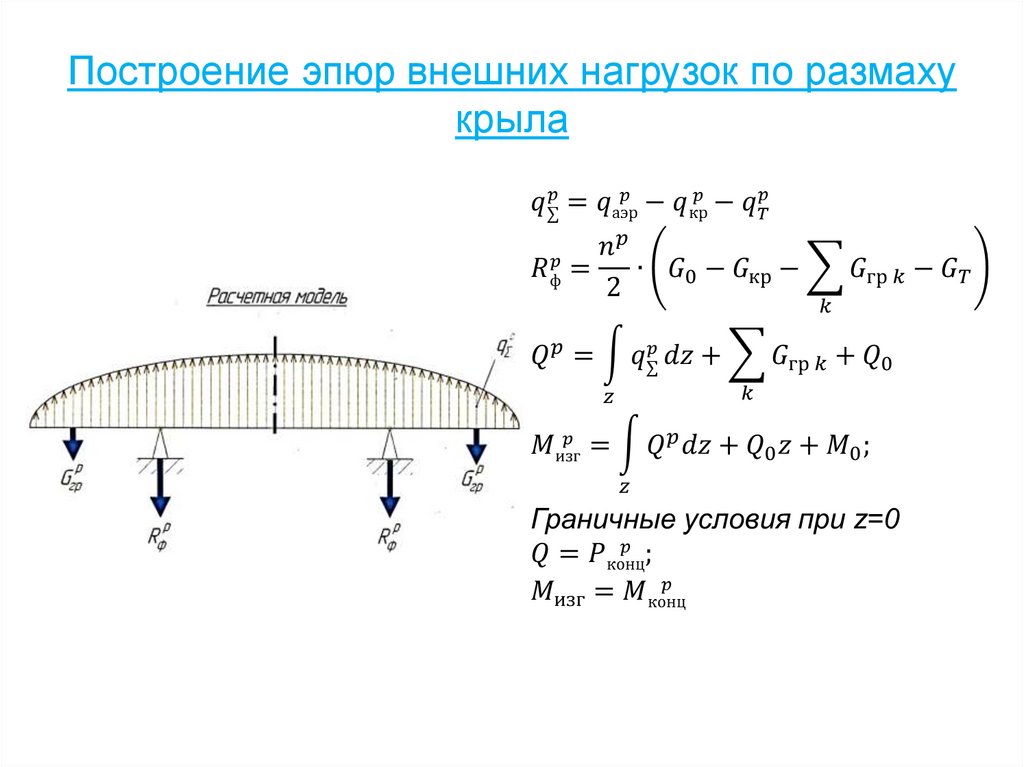
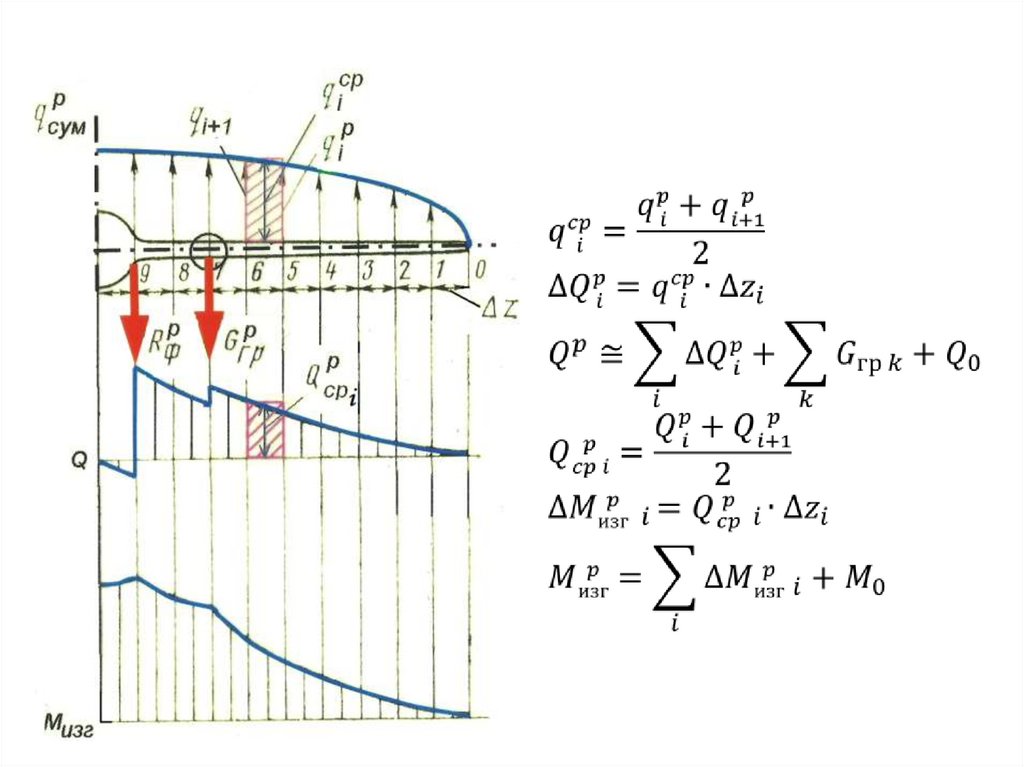
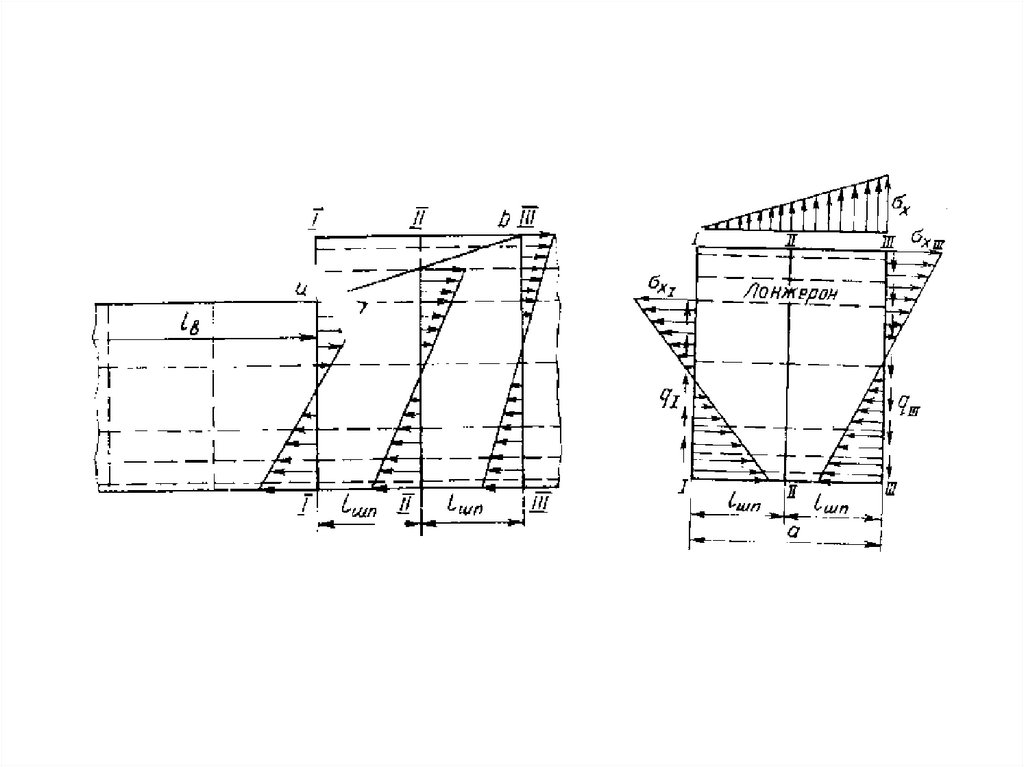
43. Построение эпюр внешних нагрузок по размаху крыла
44.
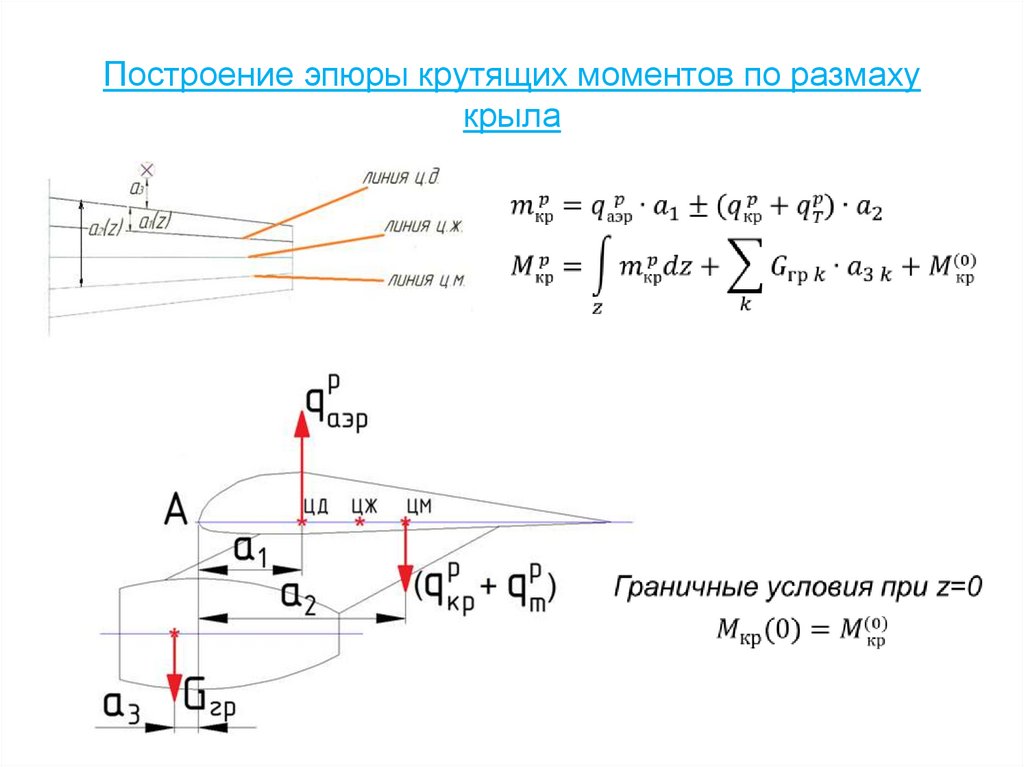
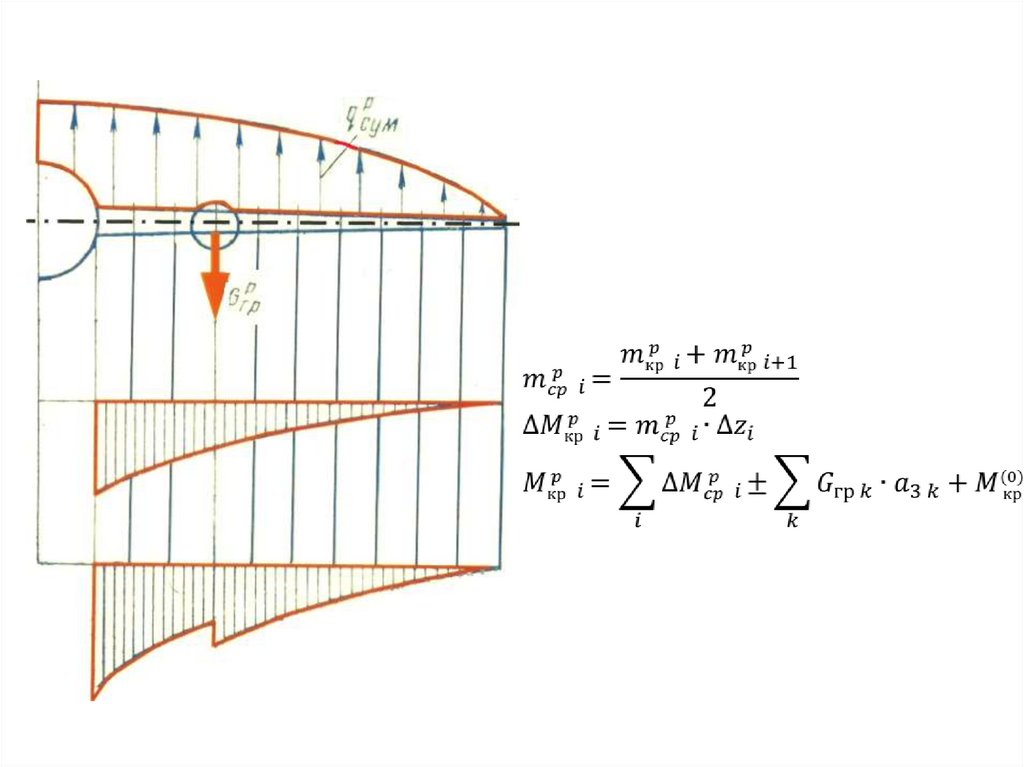
45. Построение эпюры крутящих моментов по размаху крыла
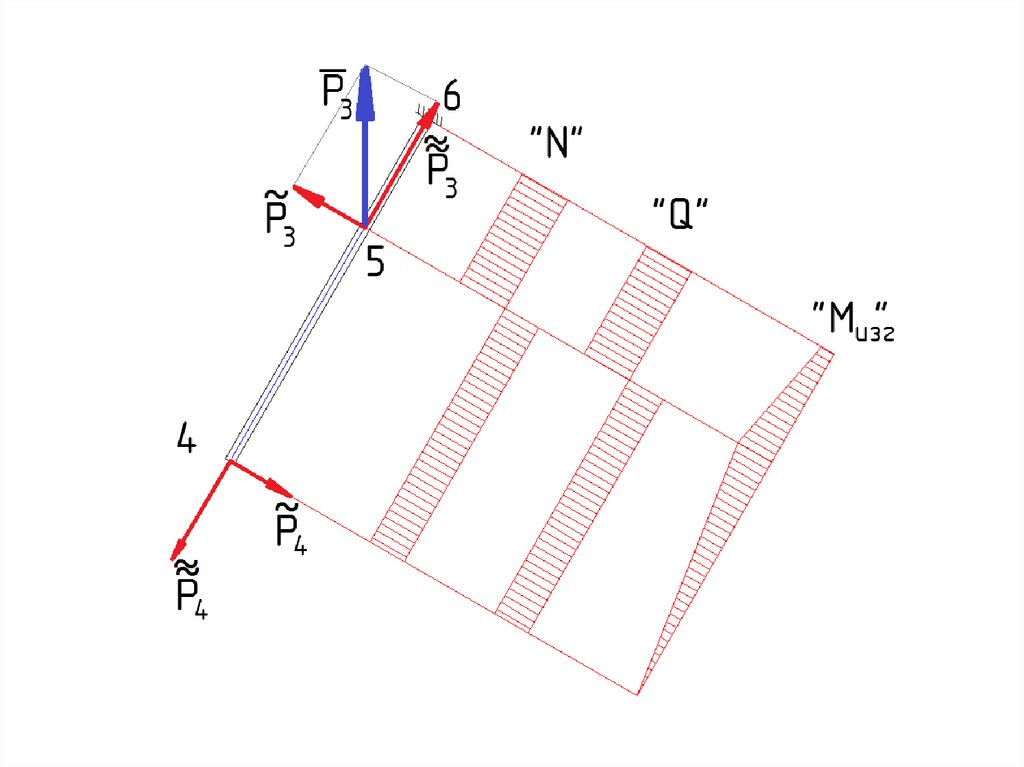
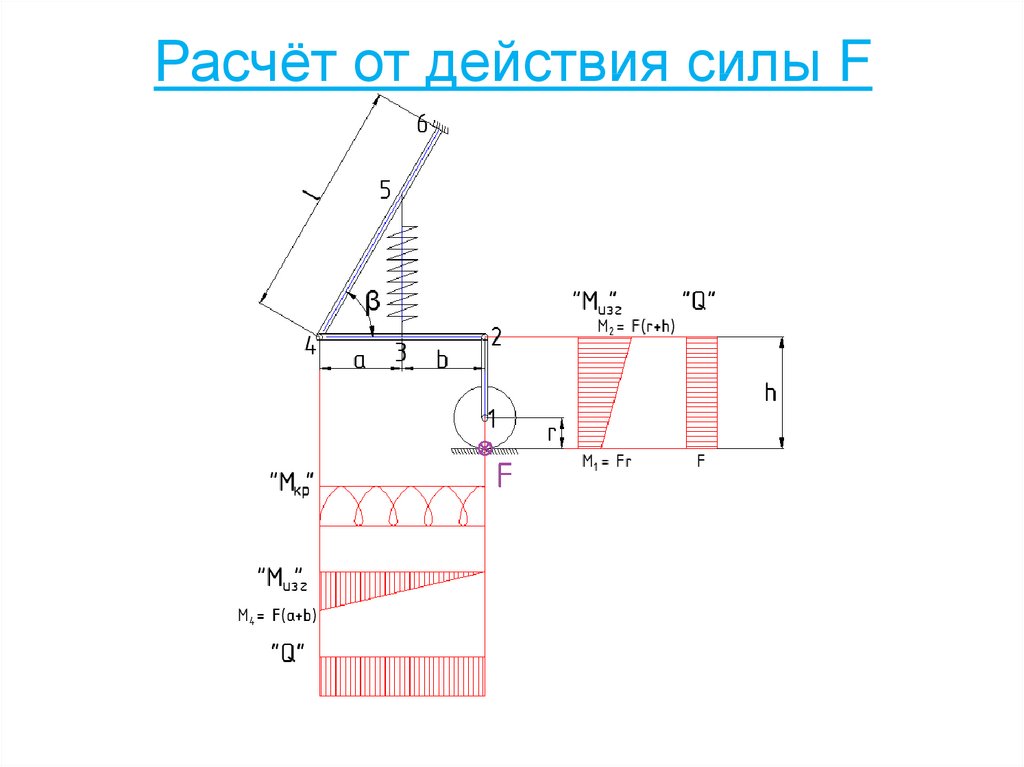
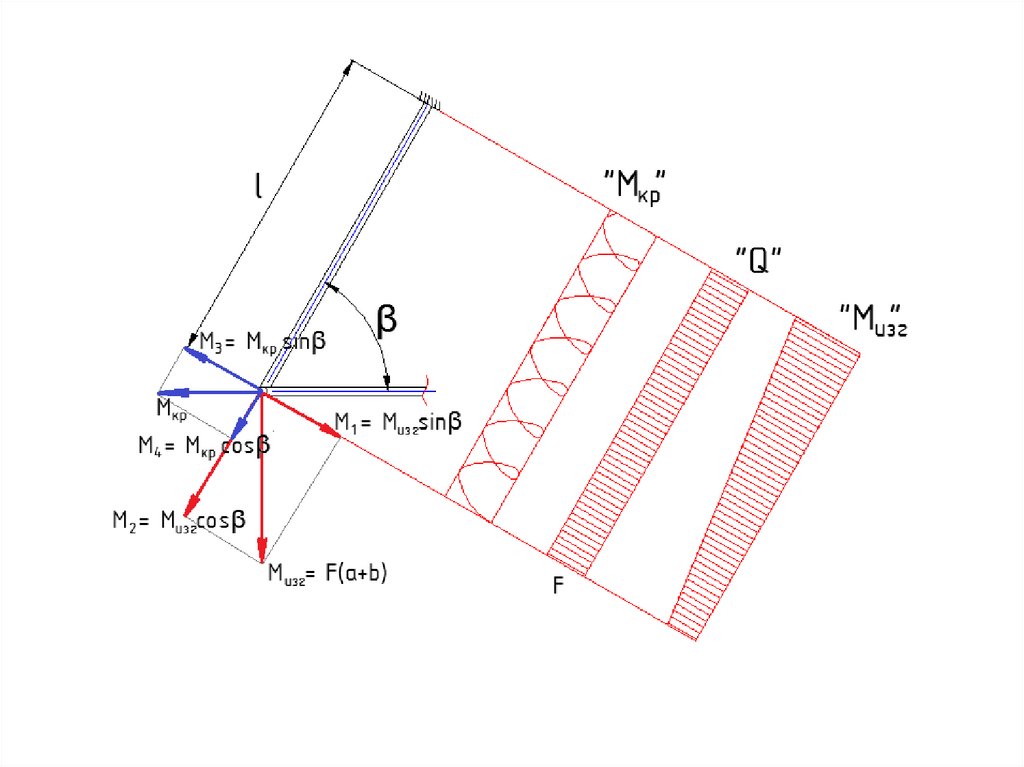
46.
47. 3. Определение расчётных (разрушающих) напряжений в силовых элементах крыла
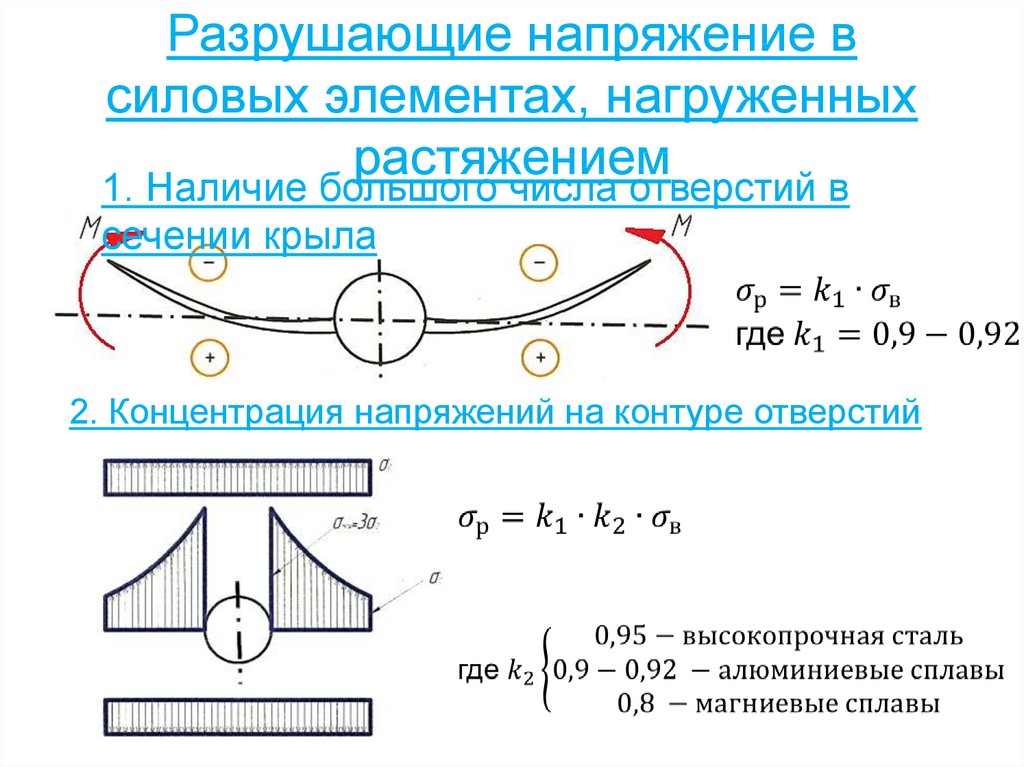
48. Разрушающие напряжение в силовых элементах, нагруженных растяжением
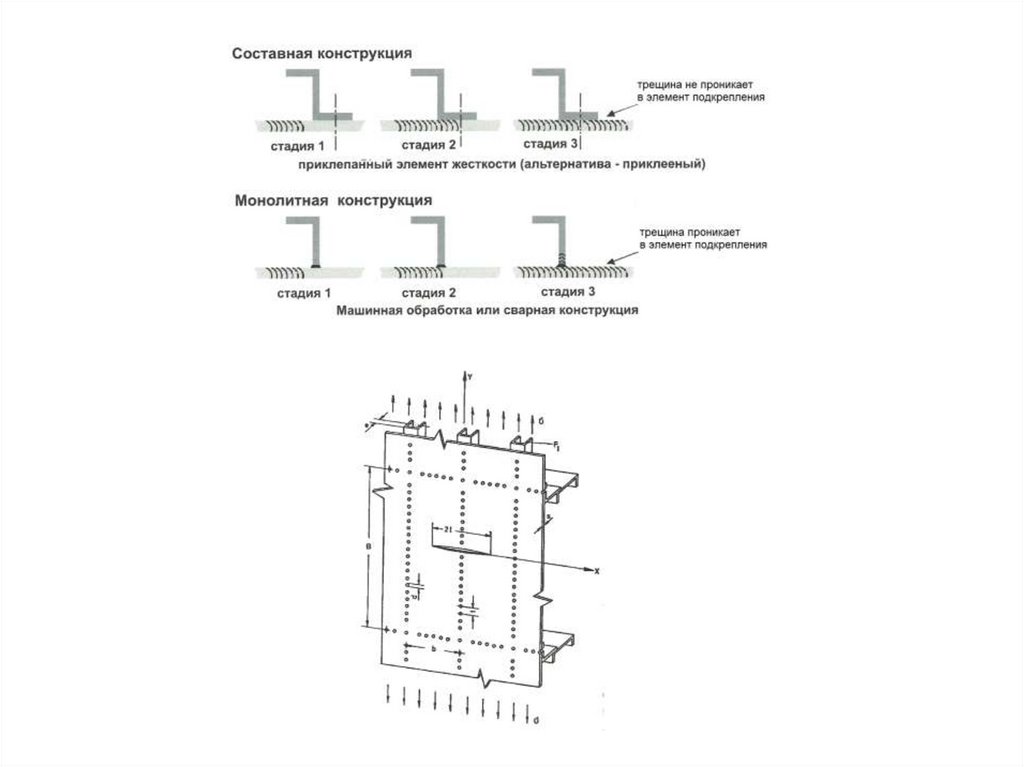
1. Наличие большого числа отверстий всечении крыла
2. Концентрация напряжений на контуре отверстий
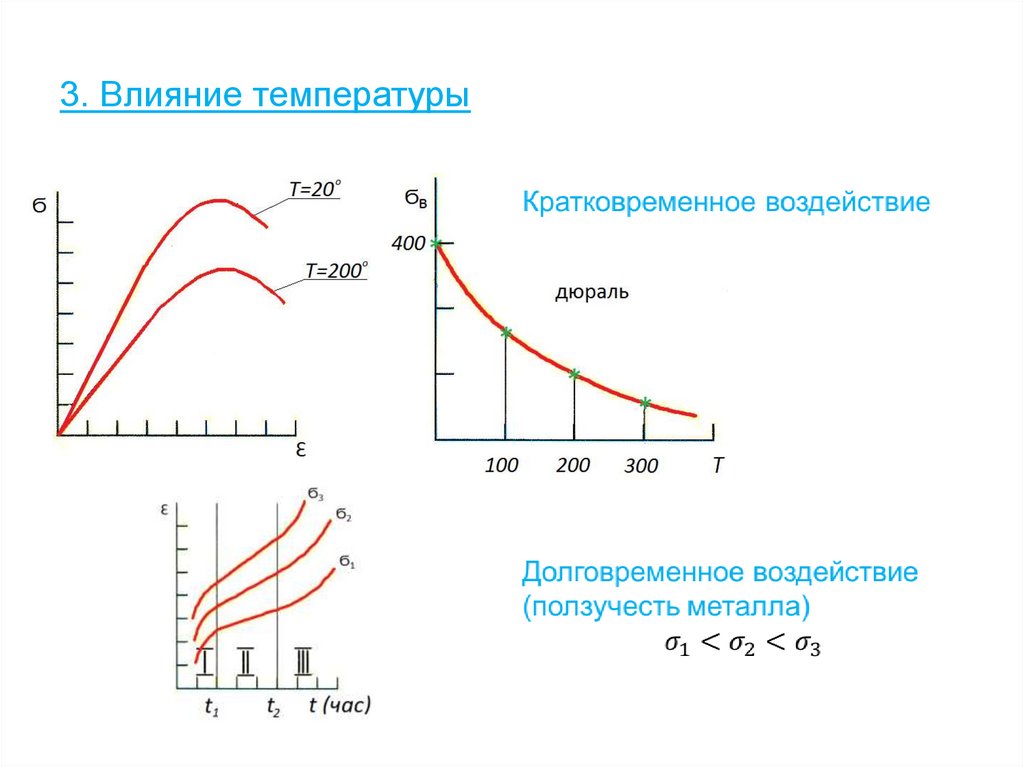
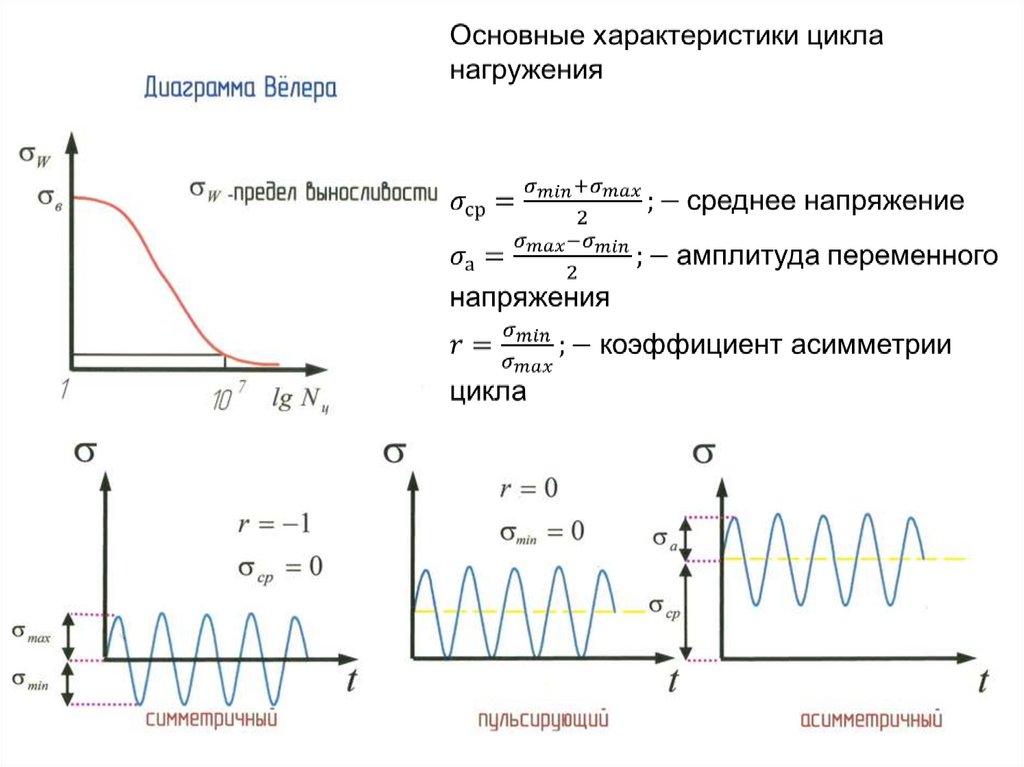
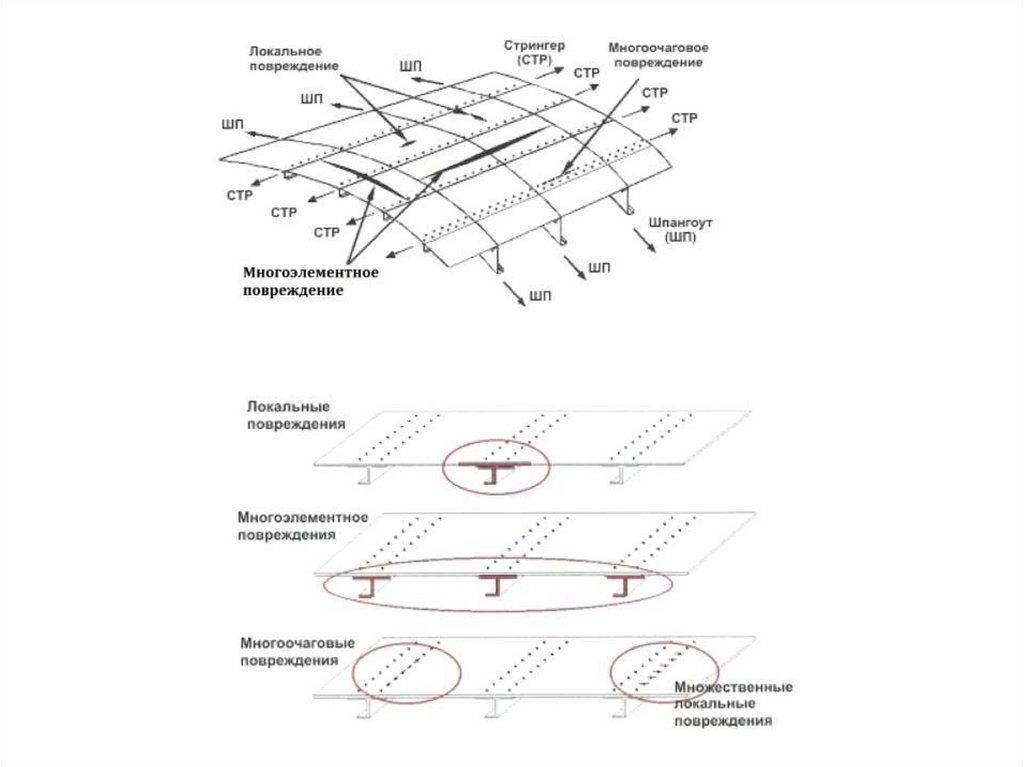
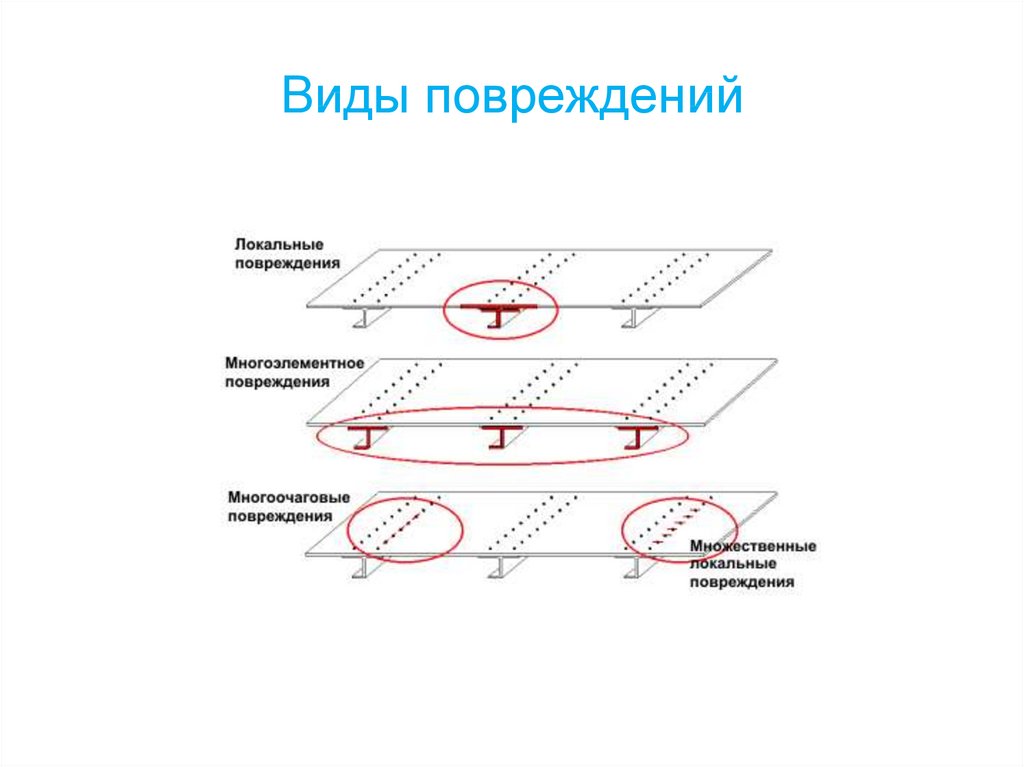
49. 3. Влияние температуры
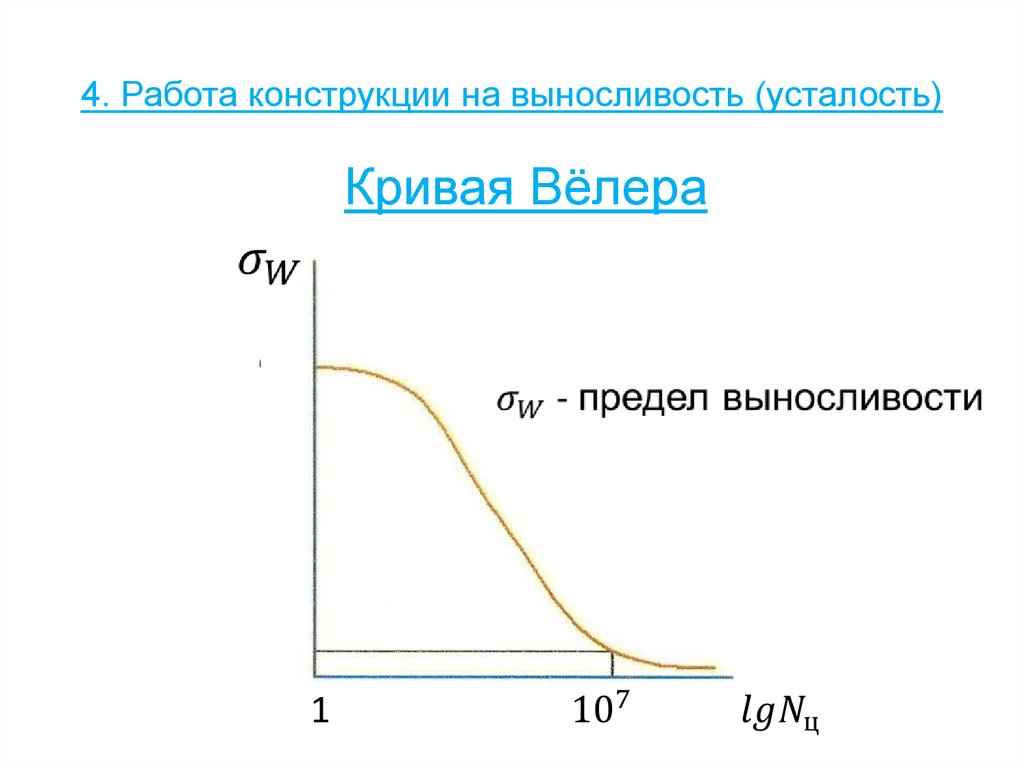
50. 4. Работа конструкции на выносливость (усталость)
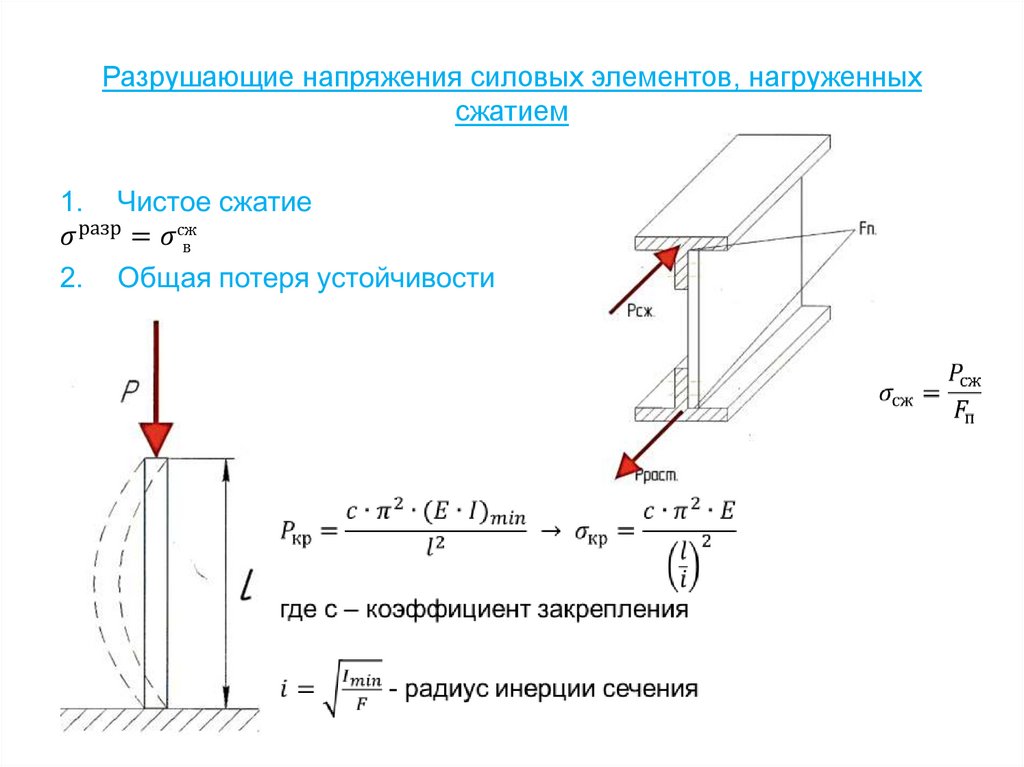
Кривая Вёлера51. Разрушающие напряжения силовых элементов, нагруженных сжатием
52.
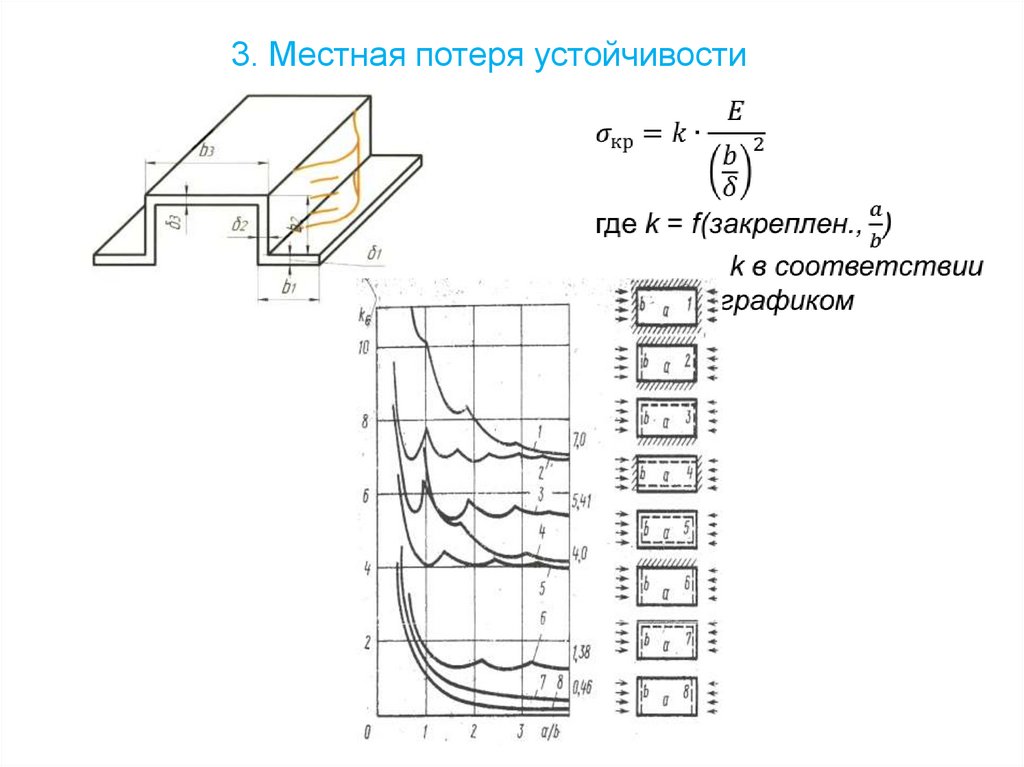
3. Местная потеря устойчивости53.
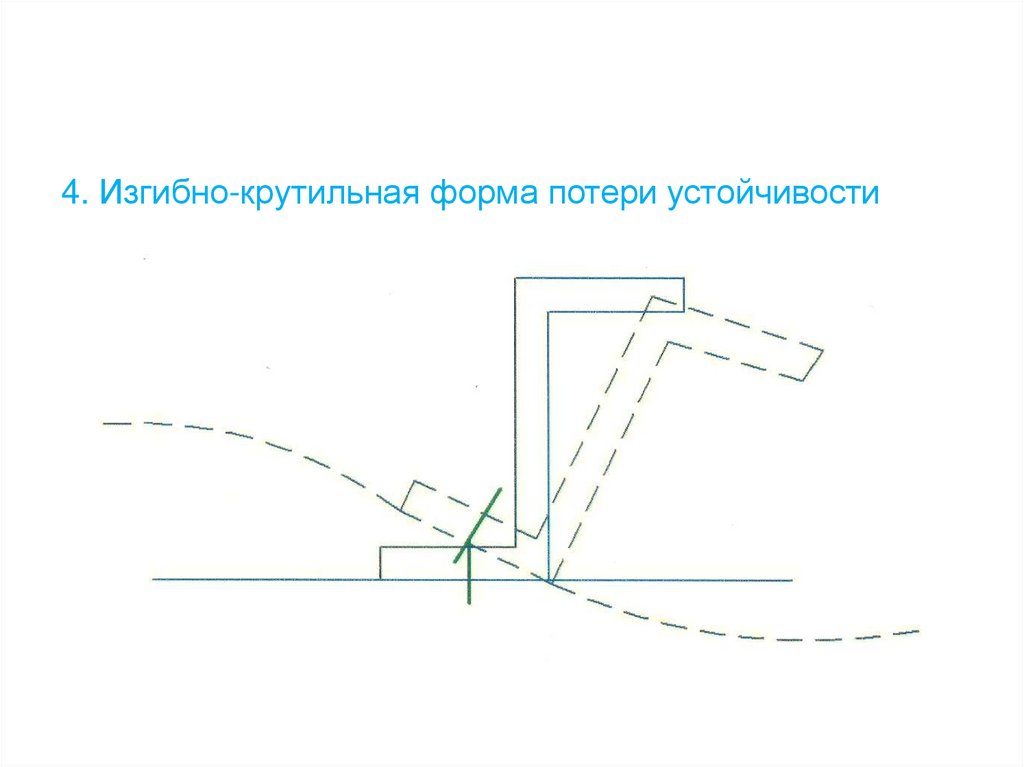
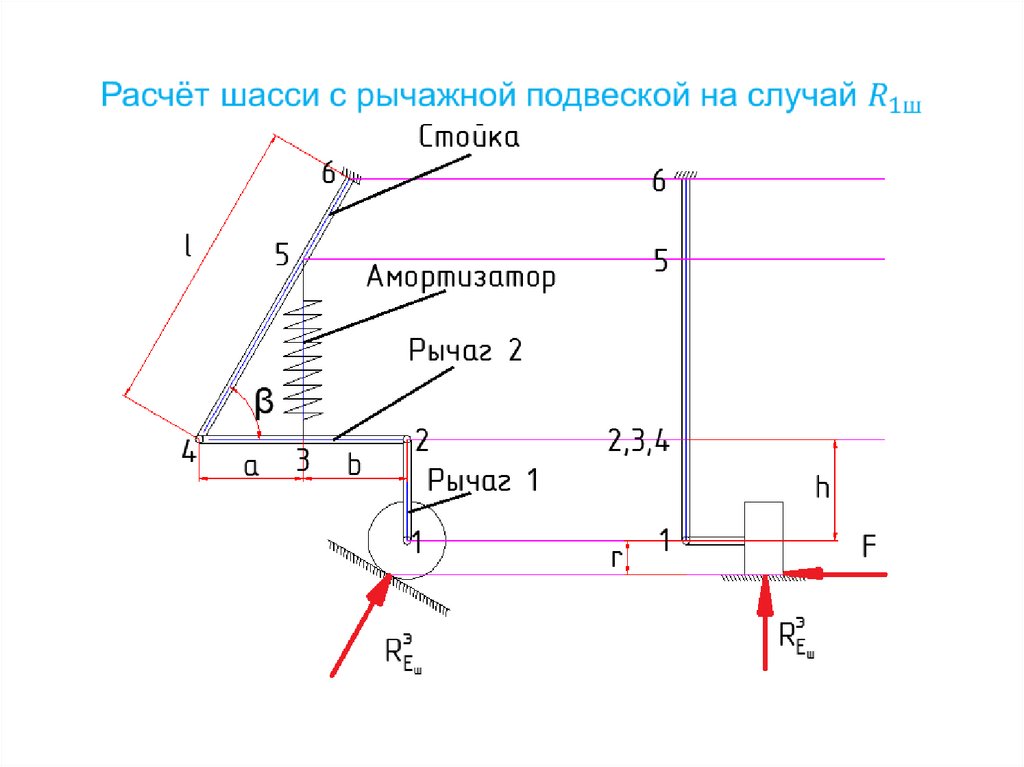
4. Изгибно-крутильная форма потери устойчивости54. Определение внешних нагрузок и расчёт на прочность шасси
55.
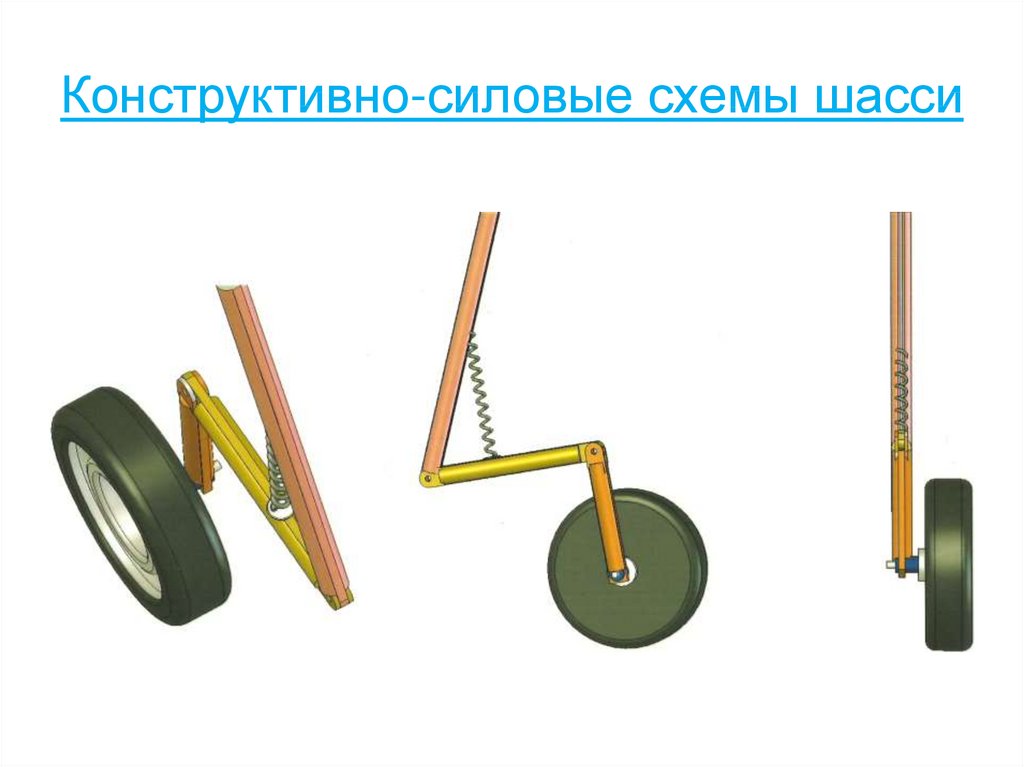
56. Конструктивно-силовые схемы шасси
57.
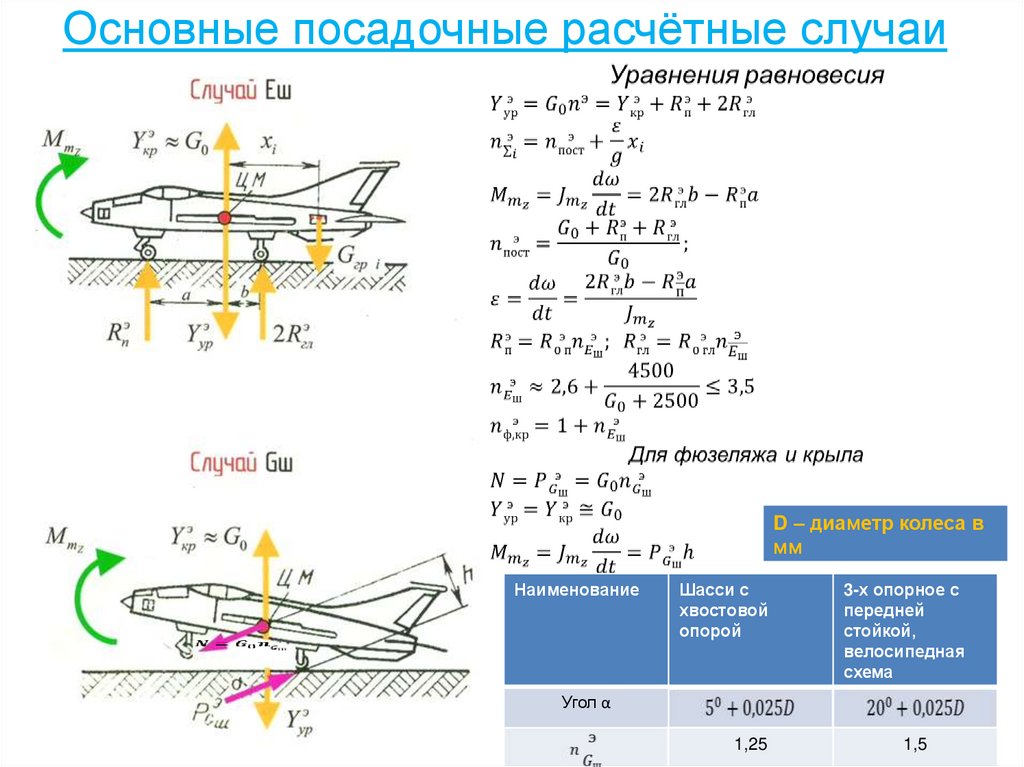
58. Основные посадочные расчётные случаи
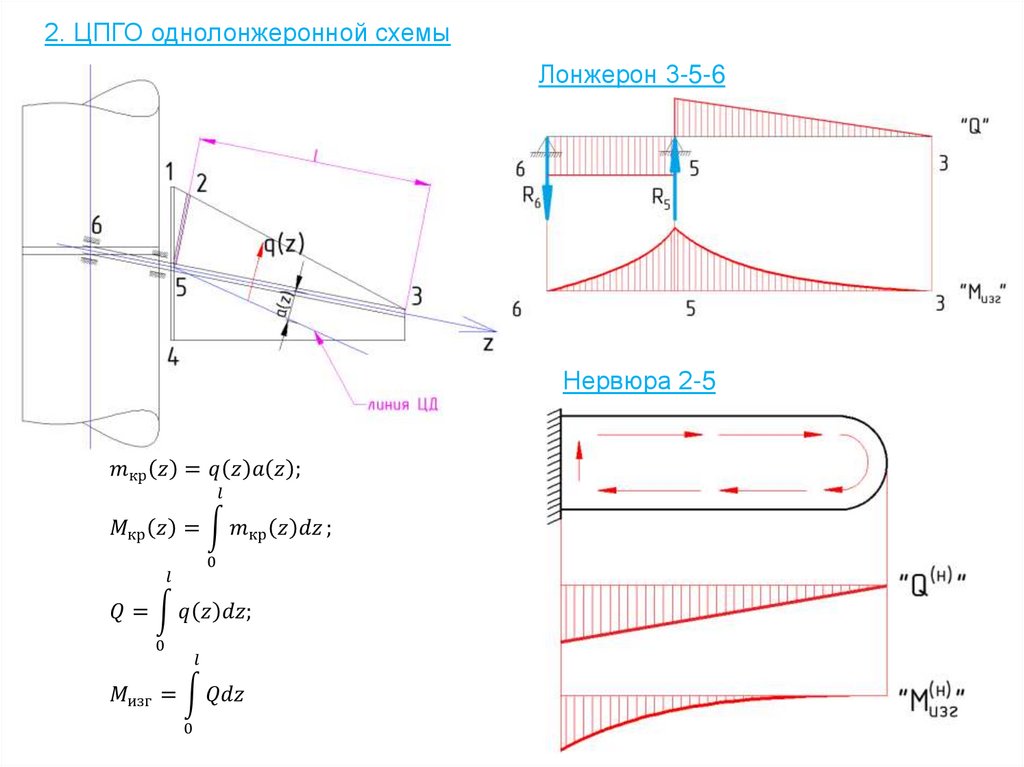
D – диаметр колеса вмм
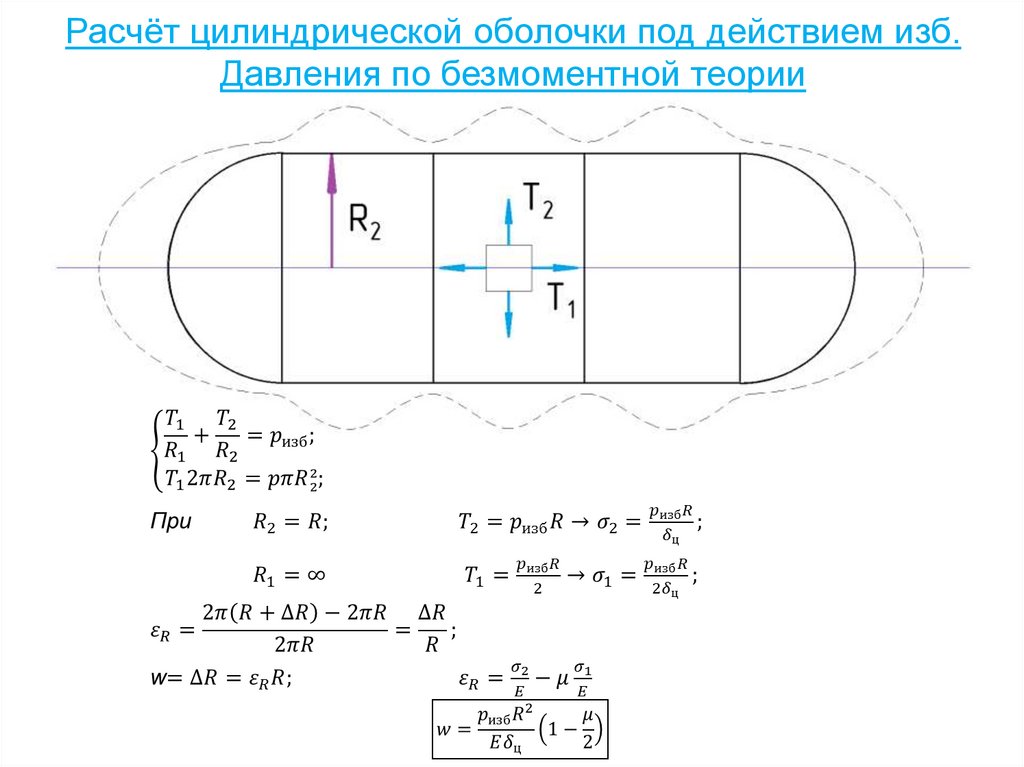
Наименование
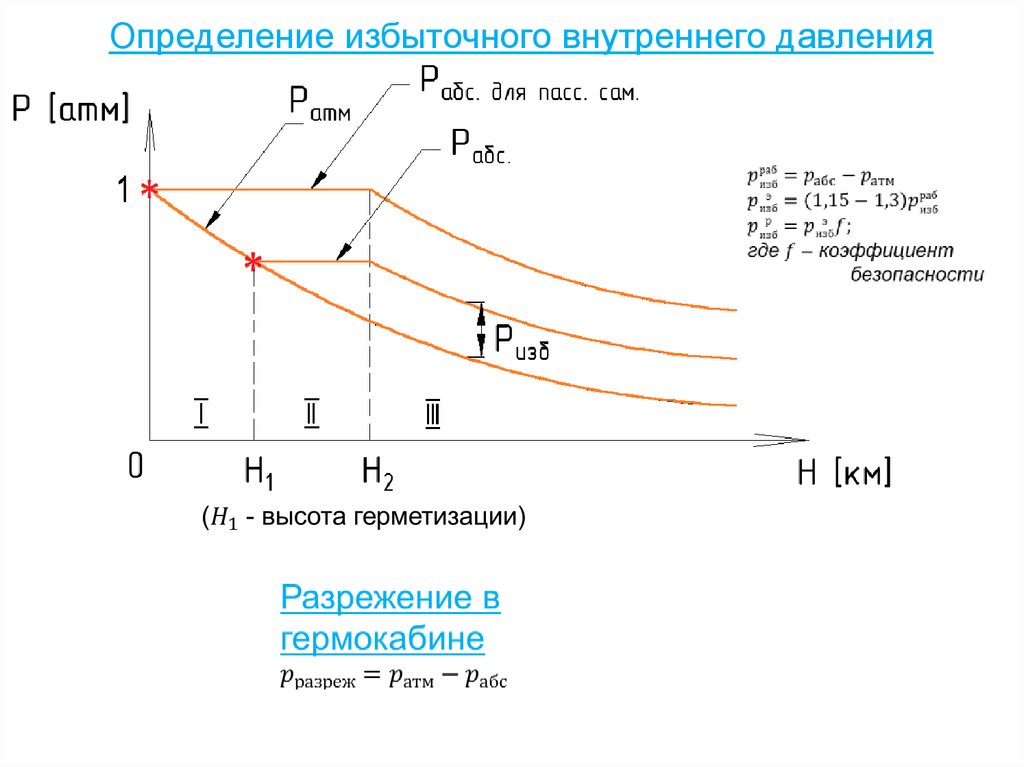
Шасси с
хвостовой
опорой
3-х опорное с
передней
стойкой,
велосипедная
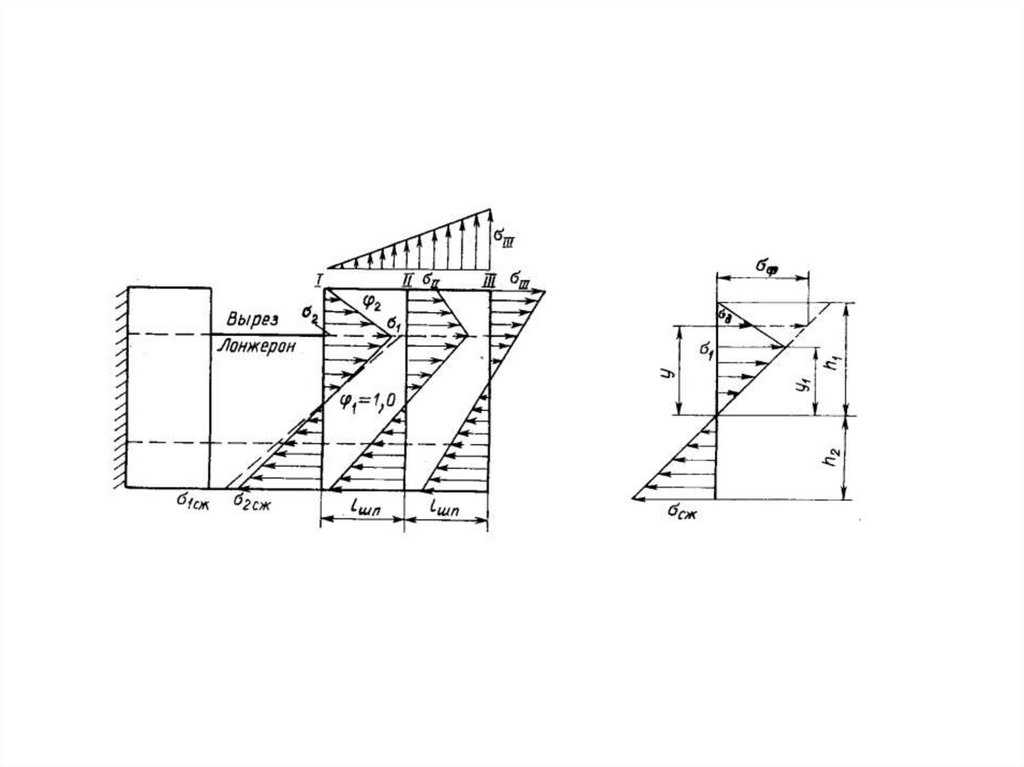
схема
Угол α
1,25
1,5
59.
60.
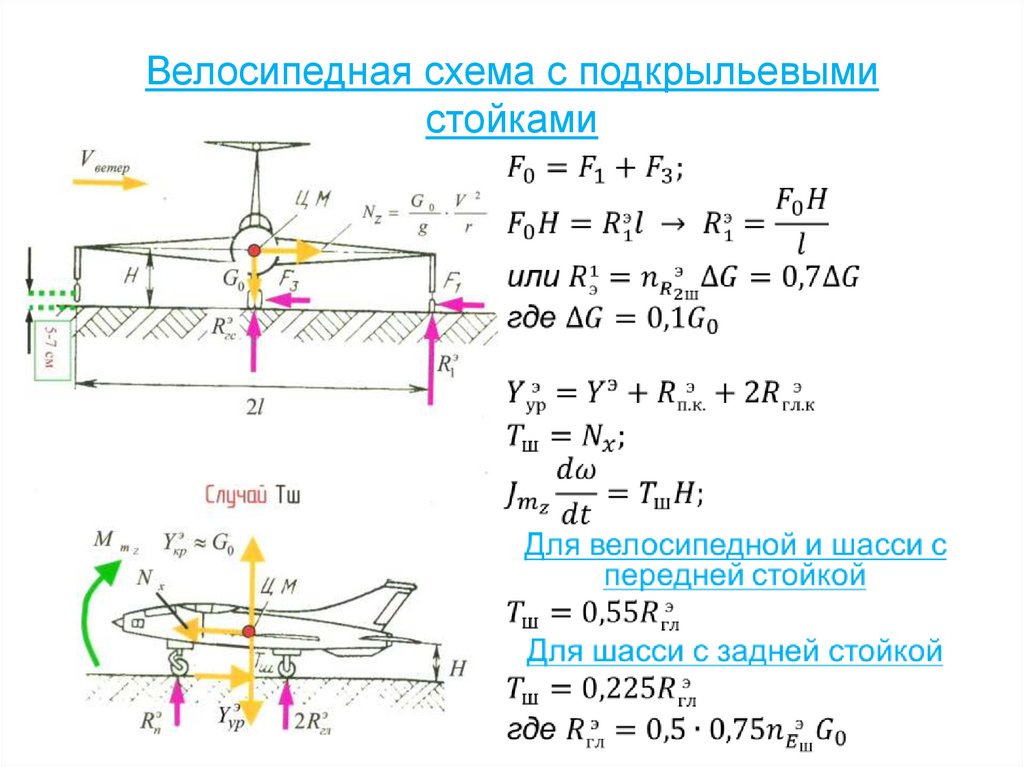
61. Велосипедная схема с подкрыльевыми стойками
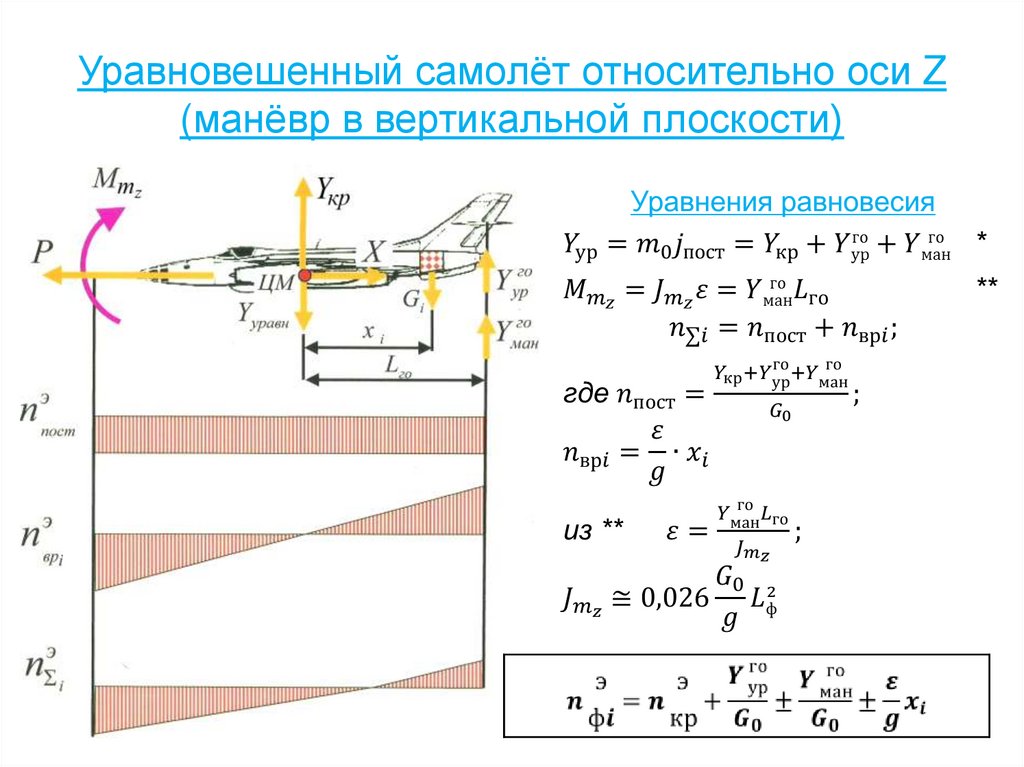
62. Уравновешенный самолёт относительно оси Z (манёвр в вертикальной плоскости)
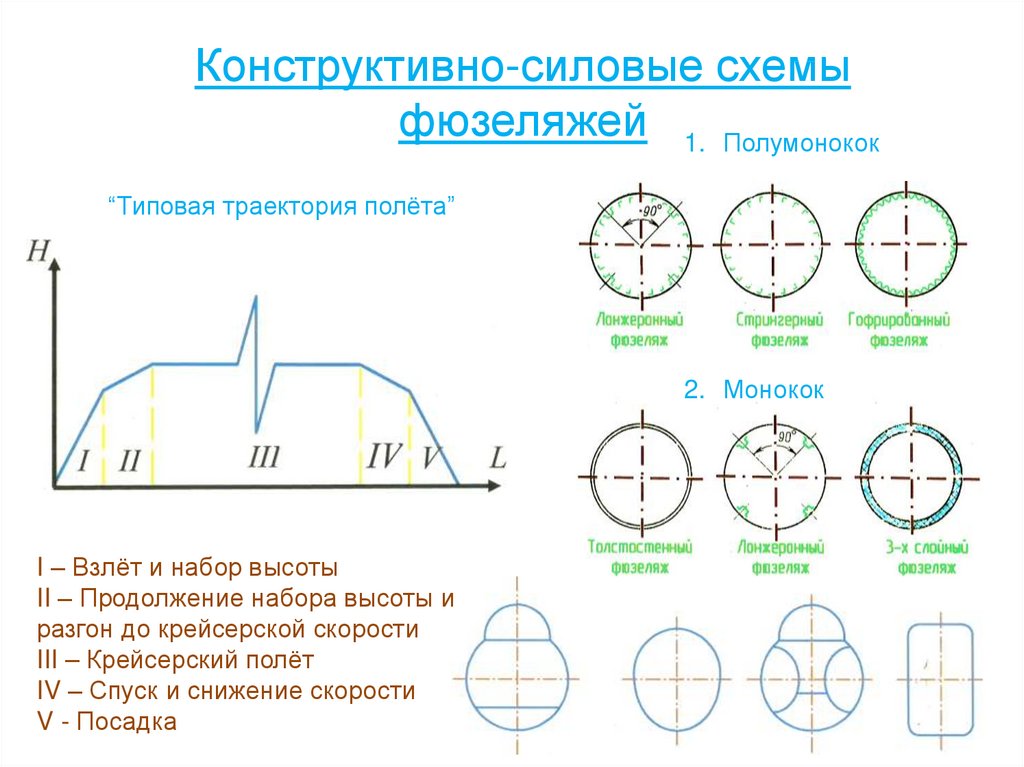
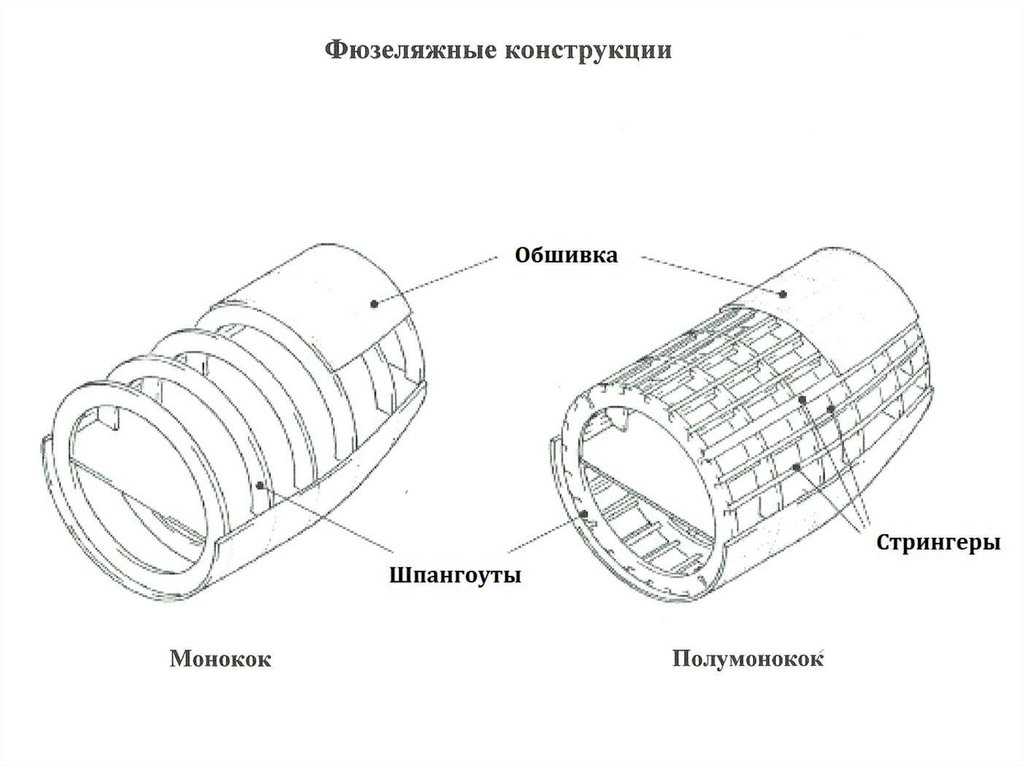
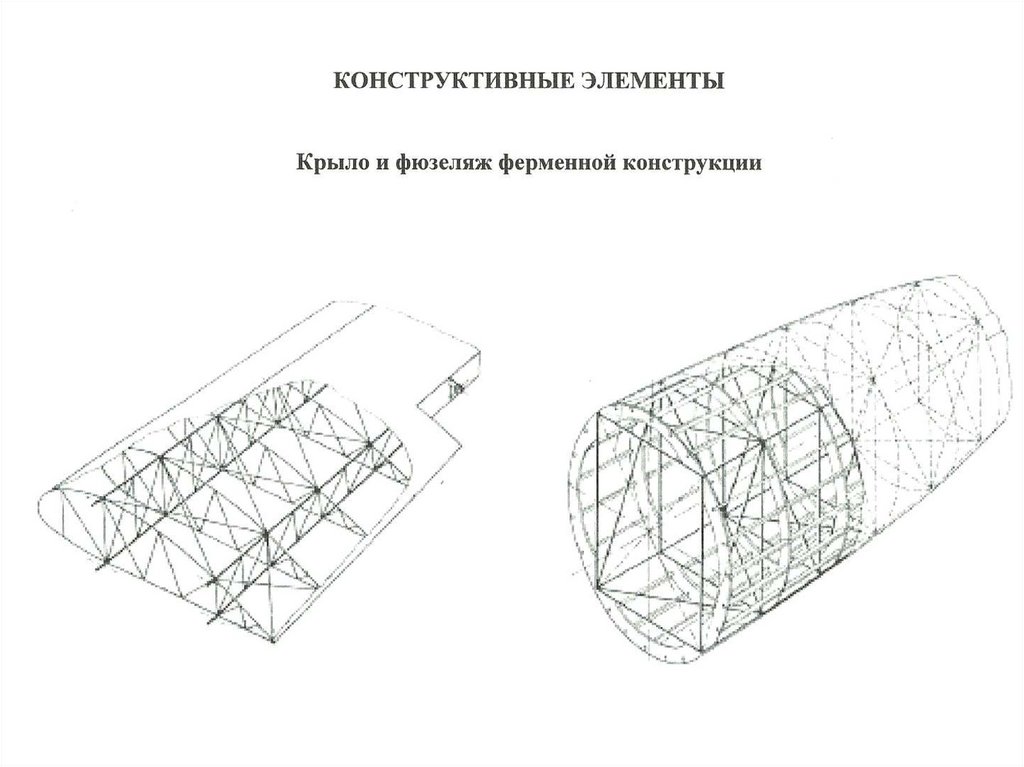
63. Конструктивно-силовые схемы фюзеляжей
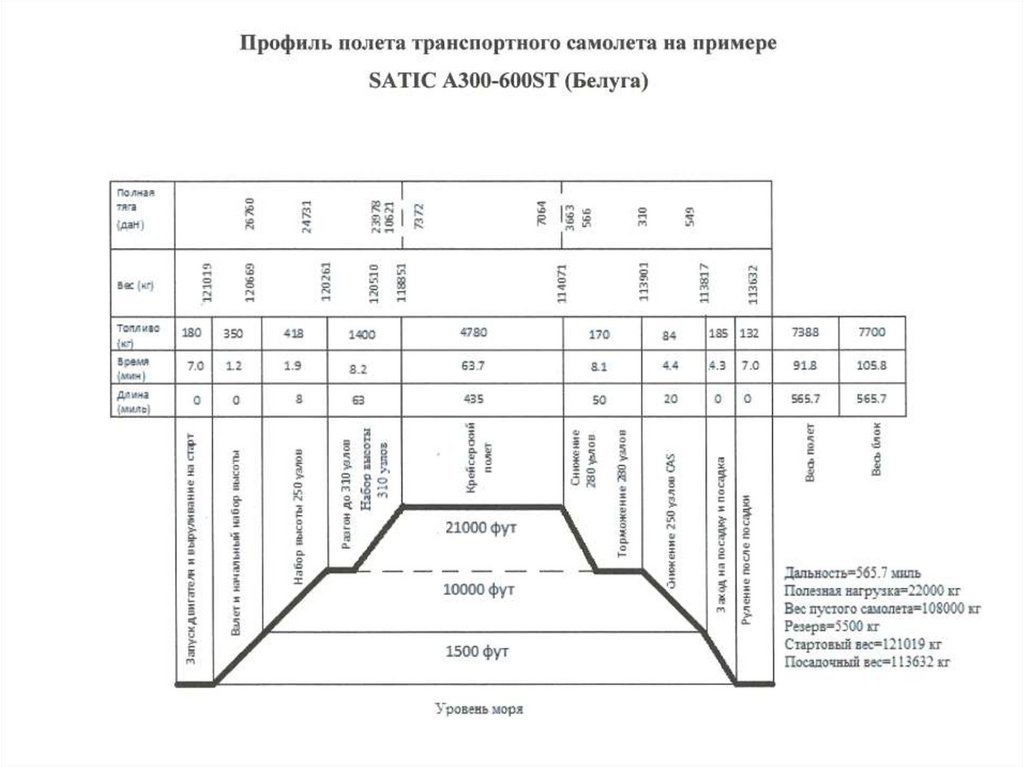
1. Полумонокок“Типовая траектория полёта”
2. Монокок
I – Взлёт и набор высоты
II – Продолжение набора высоты и
разгон до крейсерской скорости
III – Крейсерский полёт
IV – Спуск и снижение скорости
V - Посадка
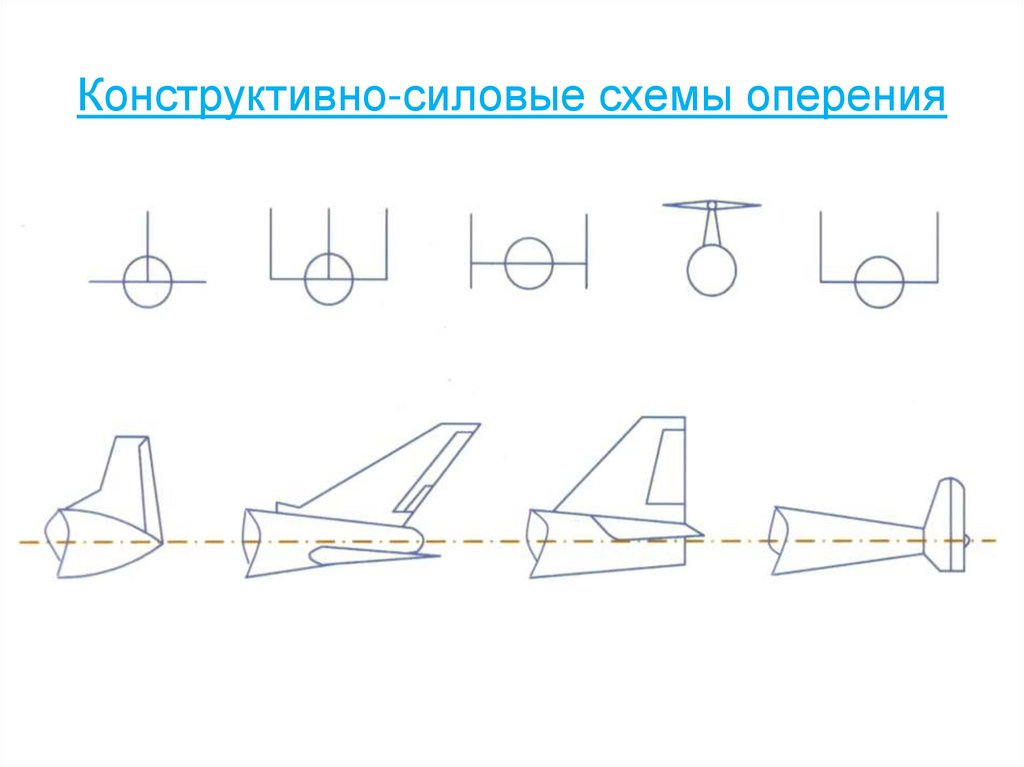
64. Конструктивно-силовые схемы оперения
65.
66.
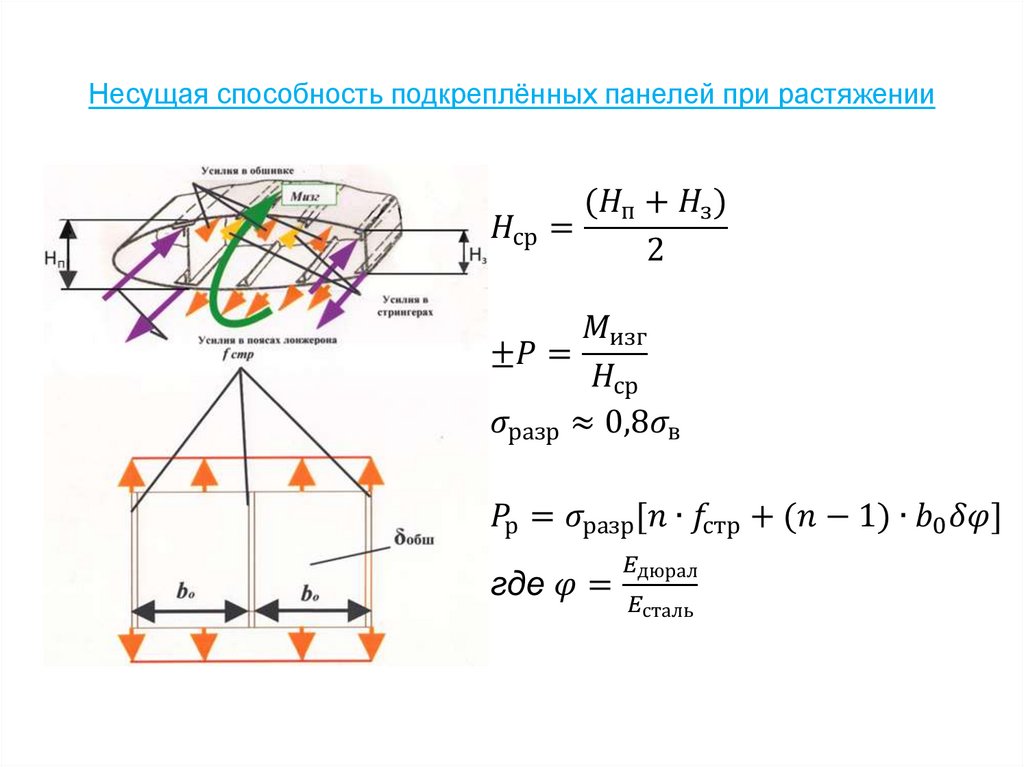
67. Несущая способность подкреплённых панелей при растяжении
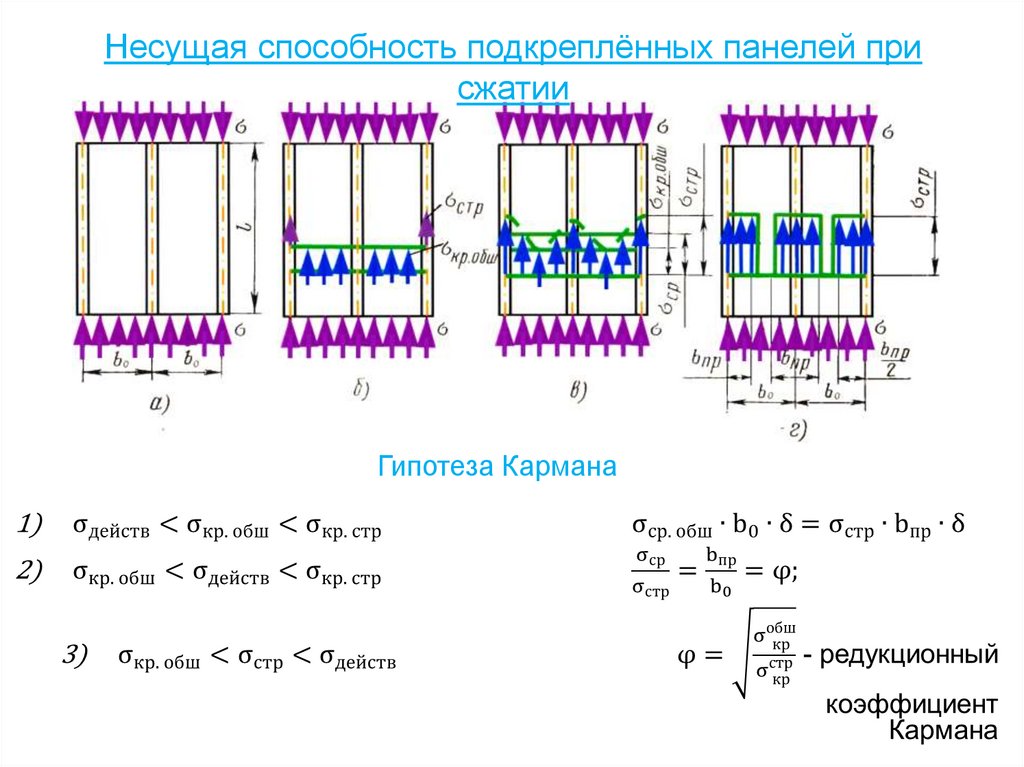
68. Несущая способность подкреплённых панелей при сжатии
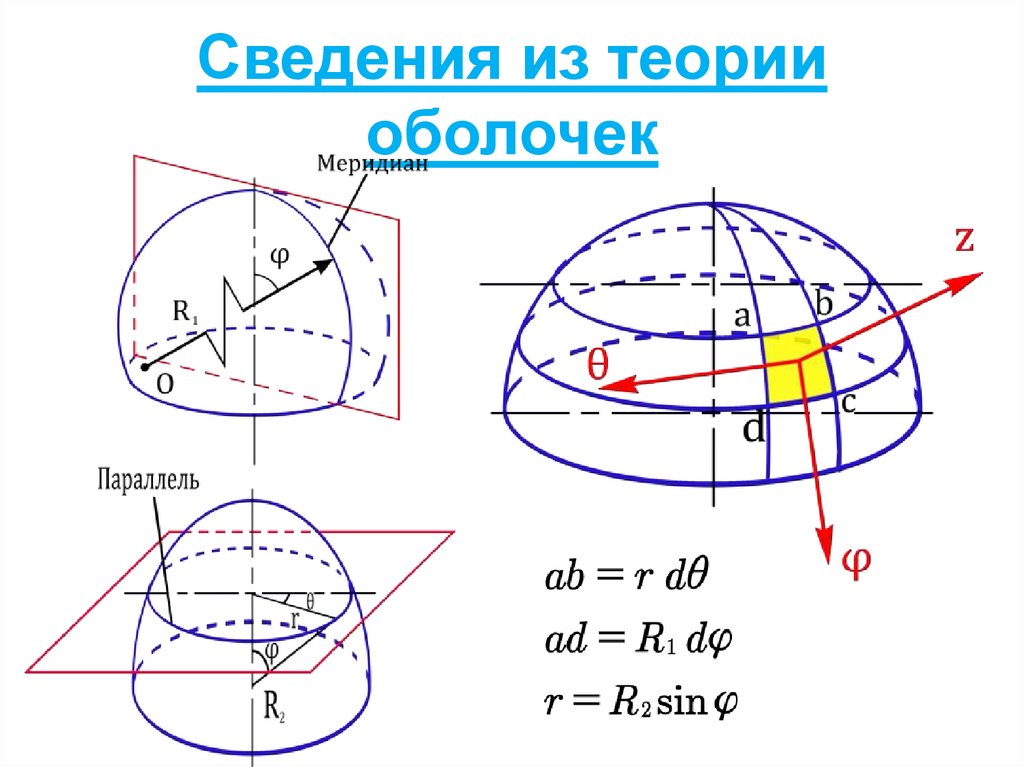
Гипотеза Кармана69. Общие методы расчёта крыла
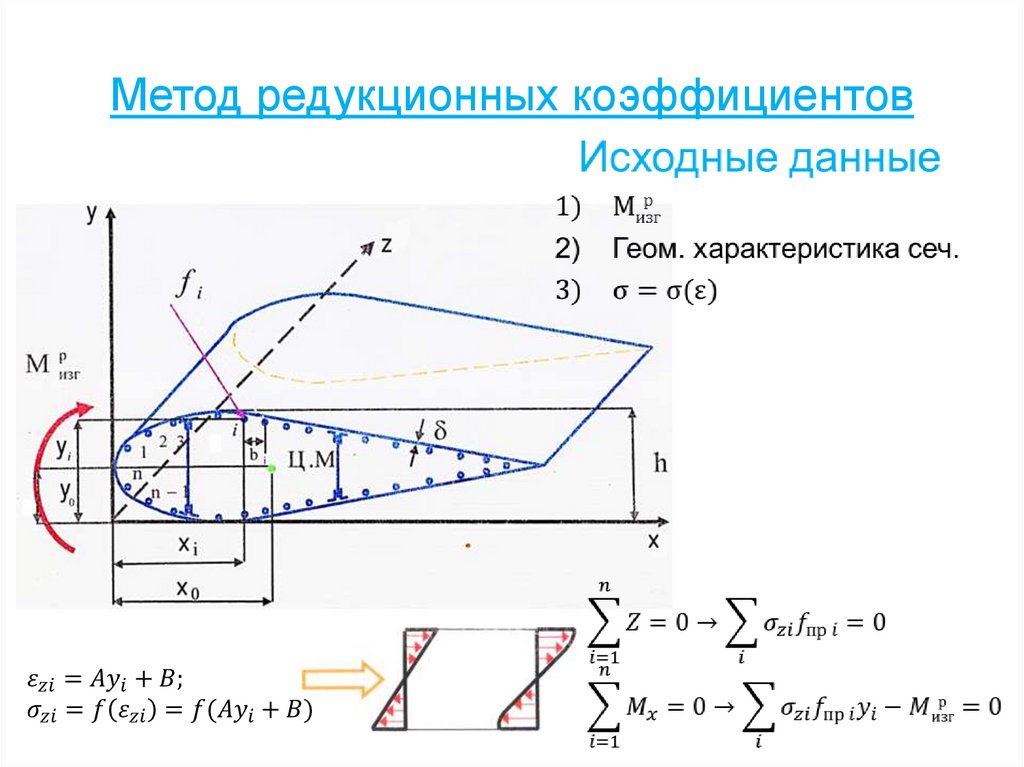
70. Метод редукционных коэффициентов
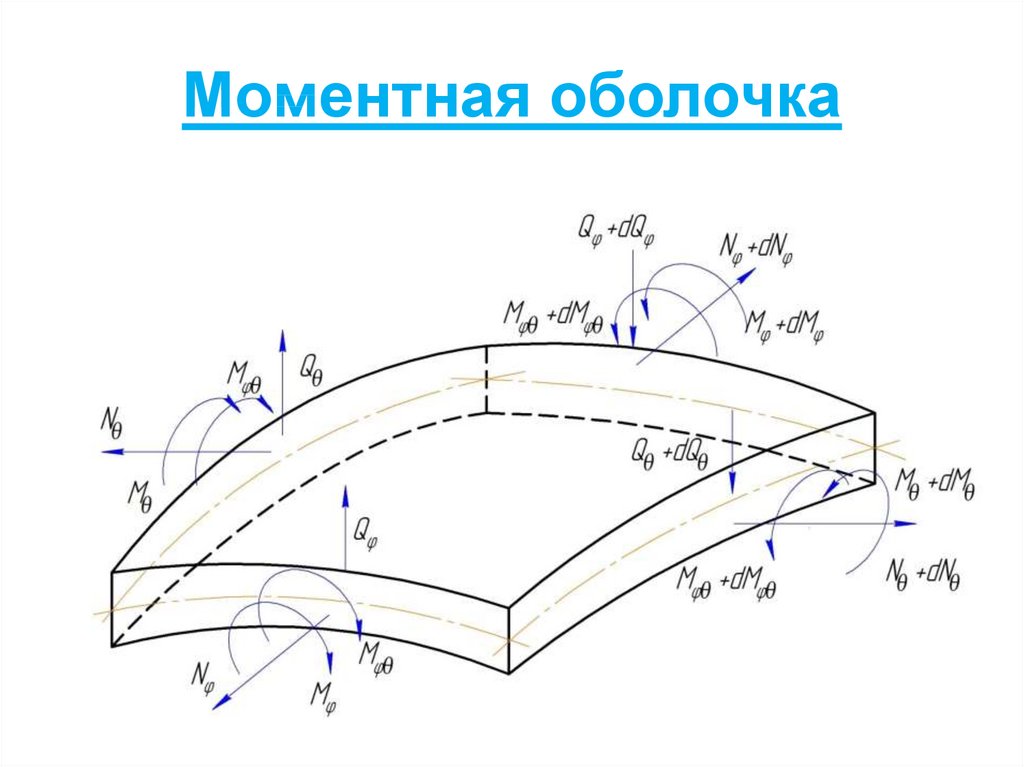
71. Основные гипотезы
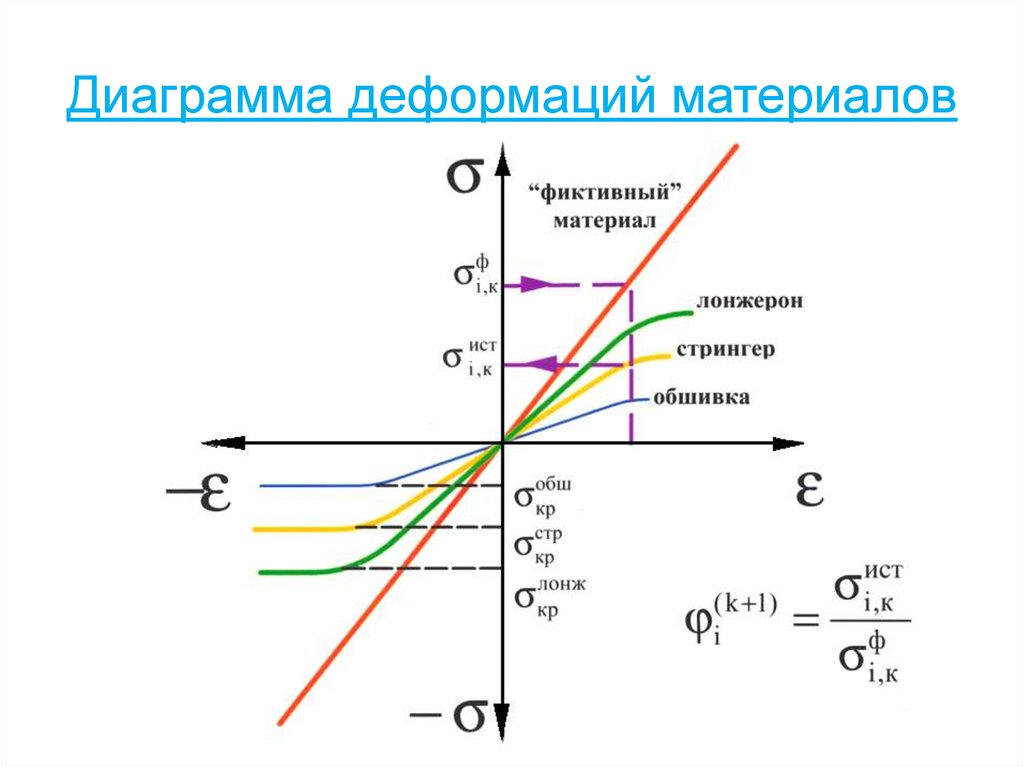
72. Диаграмма деформаций материалов
73. Процедура последовательных приближений
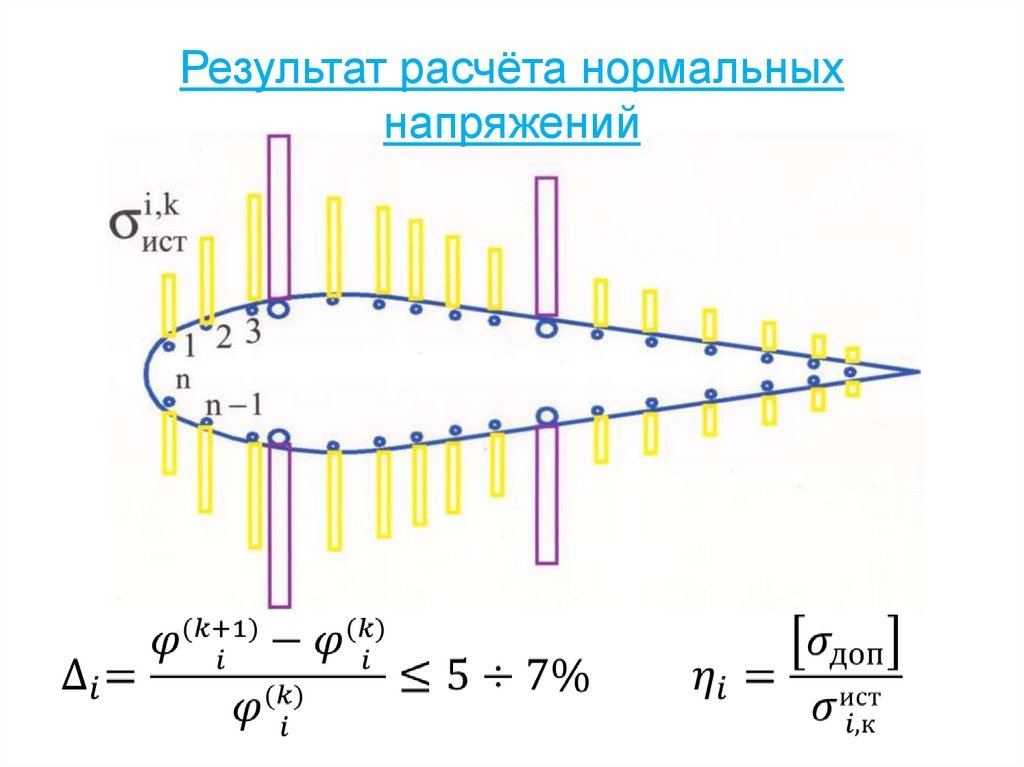
74. Результат расчёта нормальных напряжений
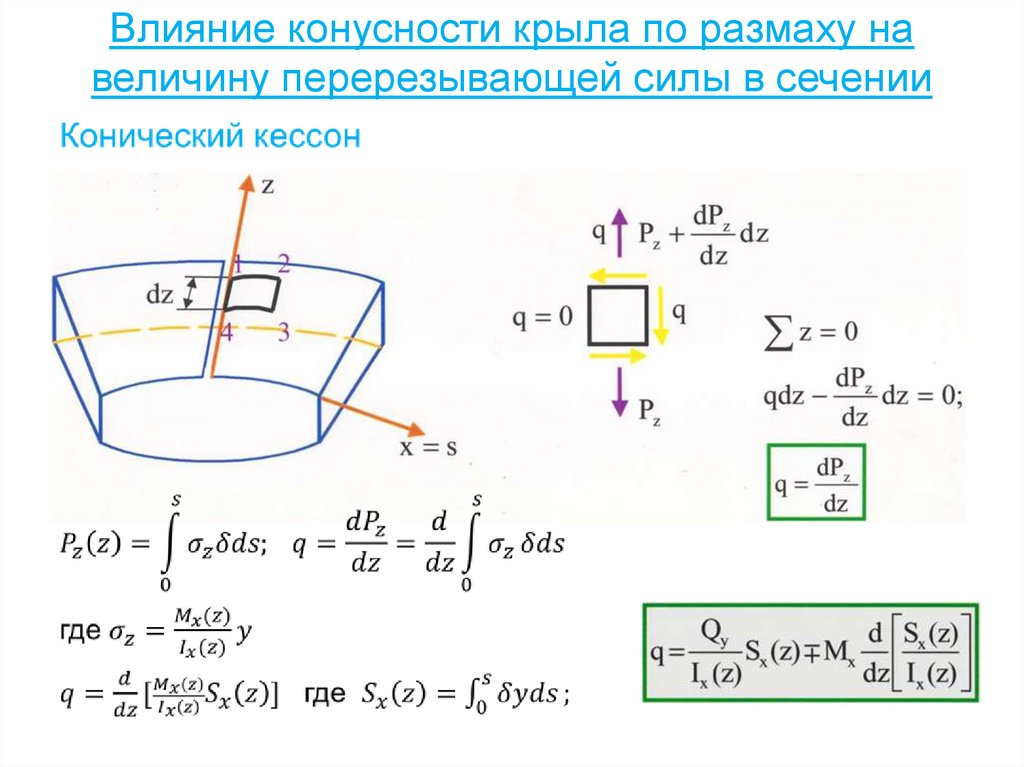
75. Влияние конусности крыла по размаху на величину перерезывающей силы в сечении
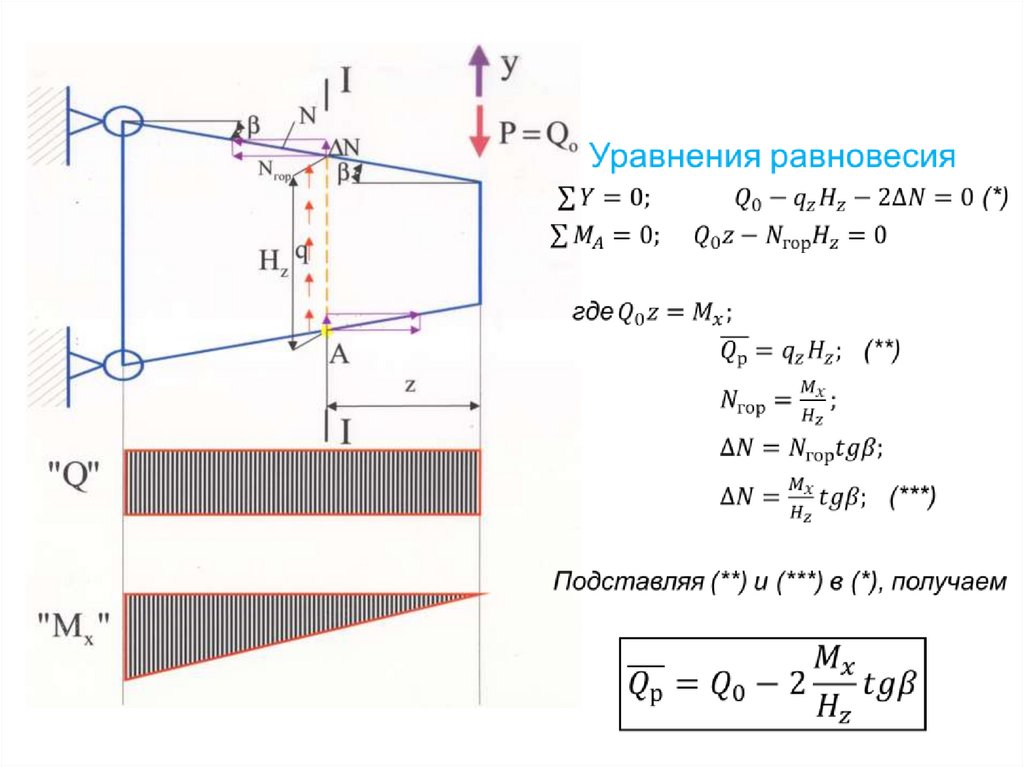
76.
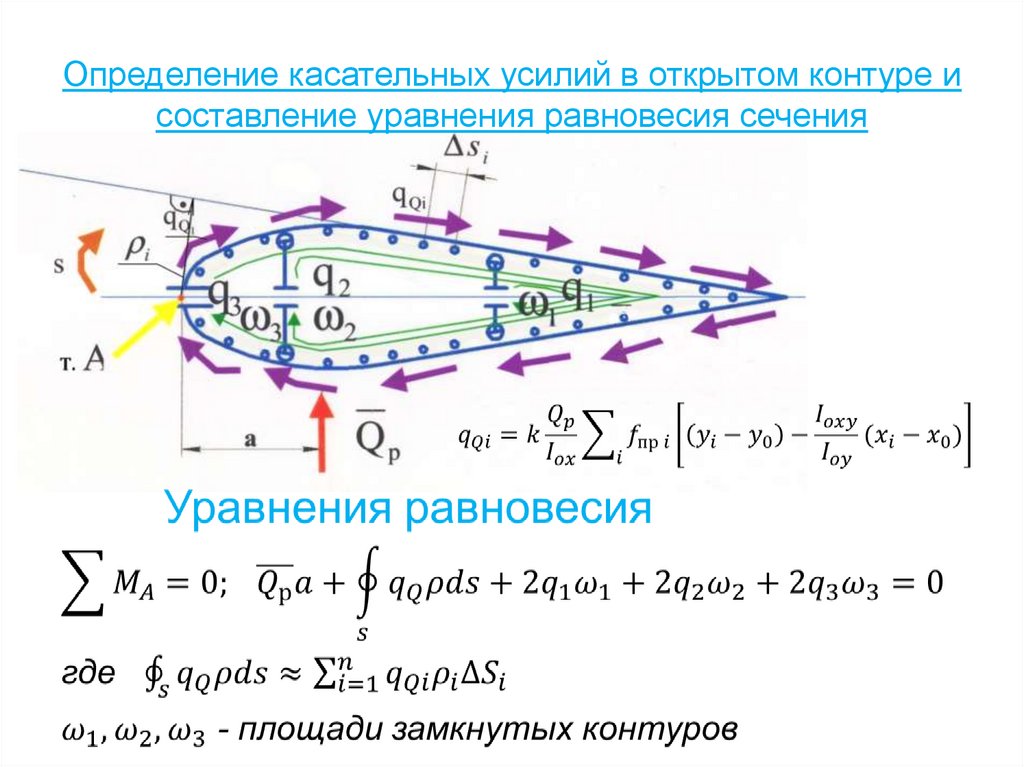
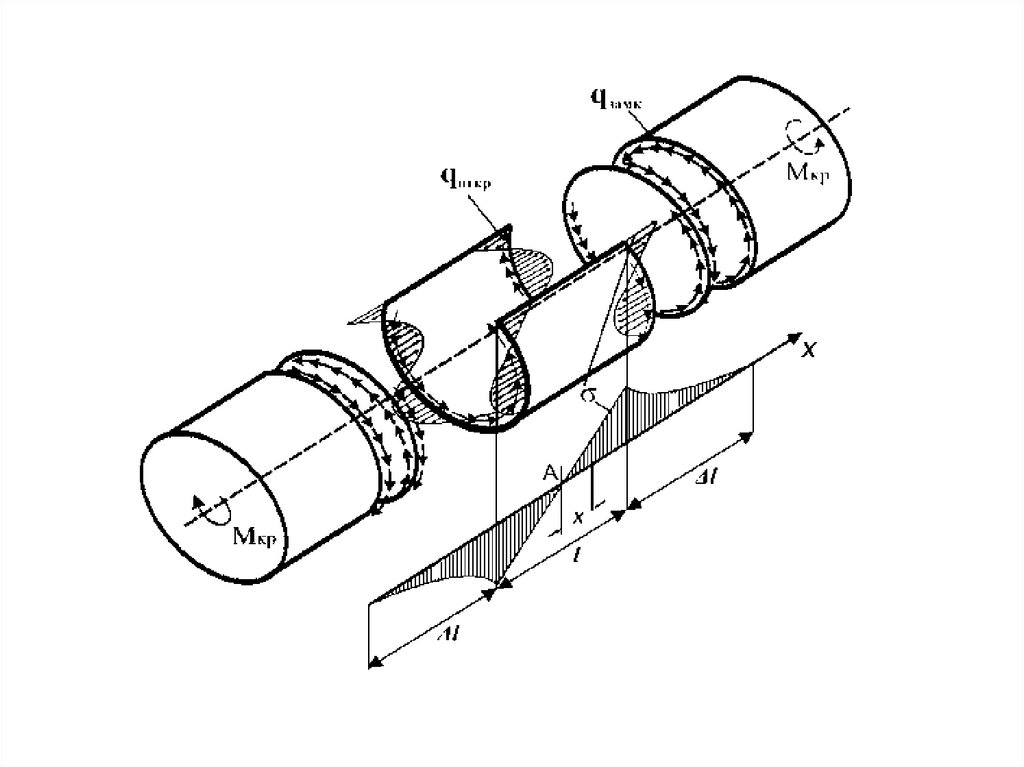
77. Определение касательных усилий в открытом контуре и составление уравнения равновесия сечения
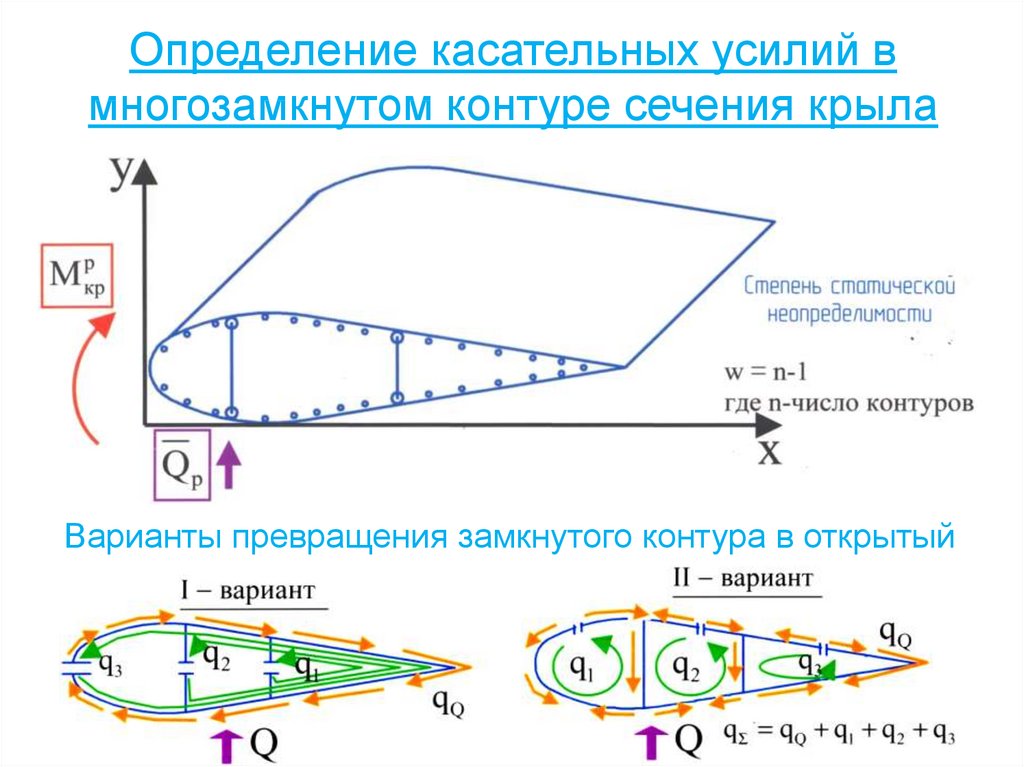
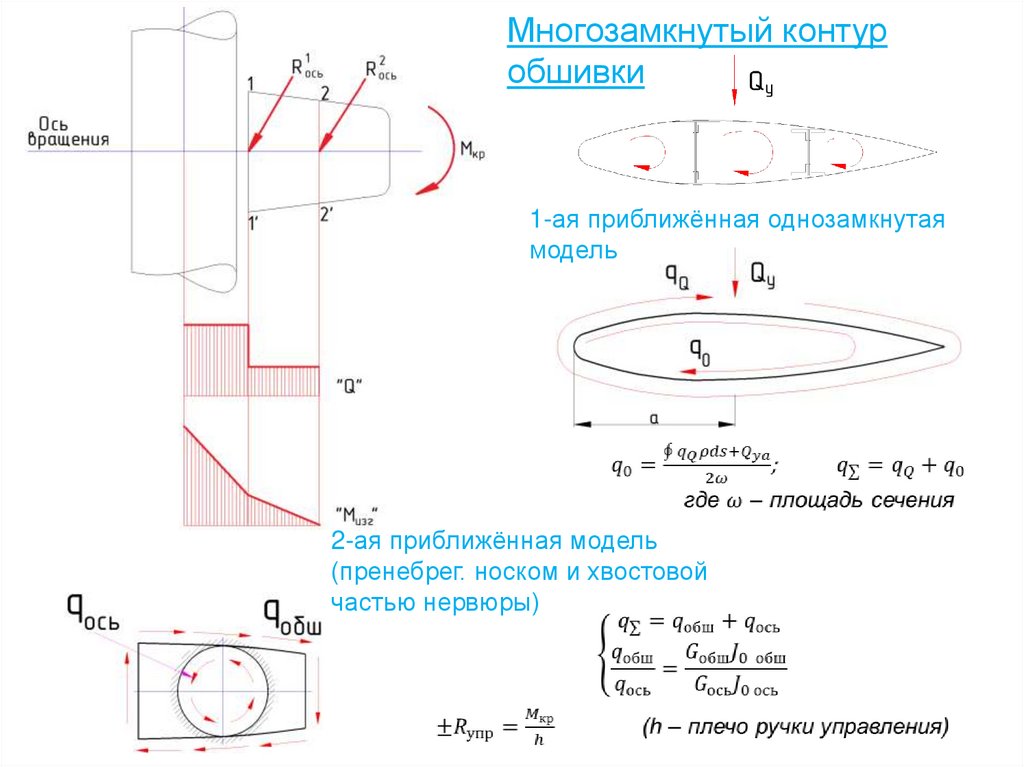
78. Определение касательных усилий в многозамкнутом контуре сечения крыла
Варианты превращения замкнутого контура в открытый79. Полная система уравнений
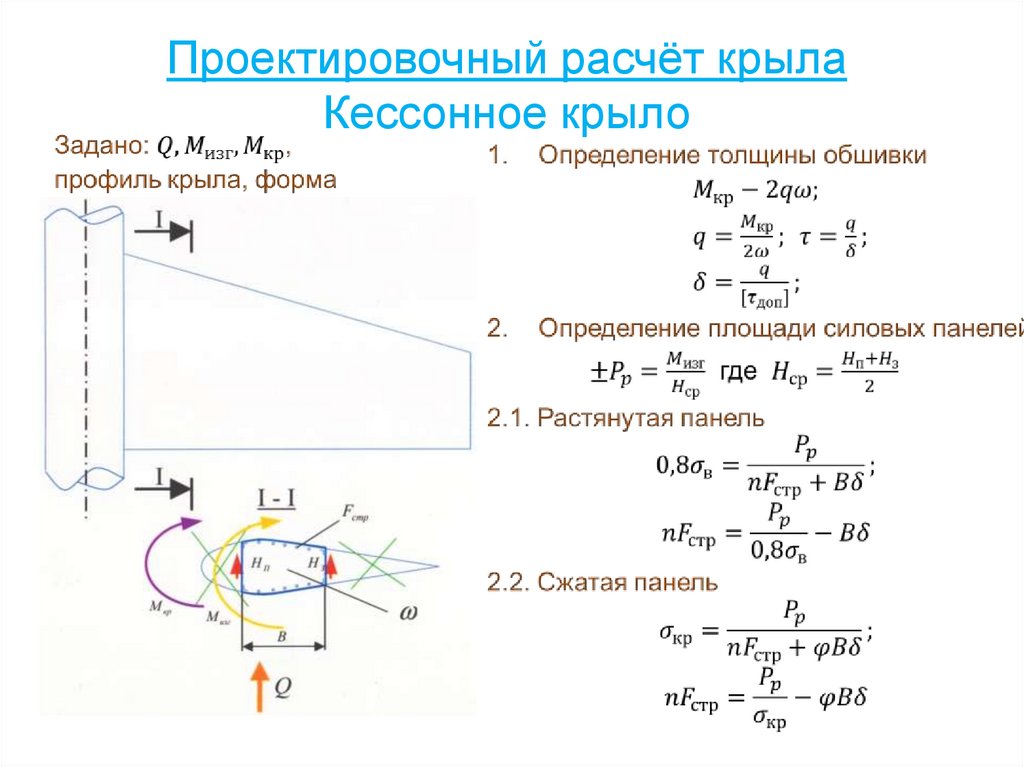
80. Проектировочный расчёт крыла Кессонное крыло
81.
82. Лонжеронное крыло
1. Определение толщиныобшивки и стенок
лонжеронов, так же как в
кессонном крыле
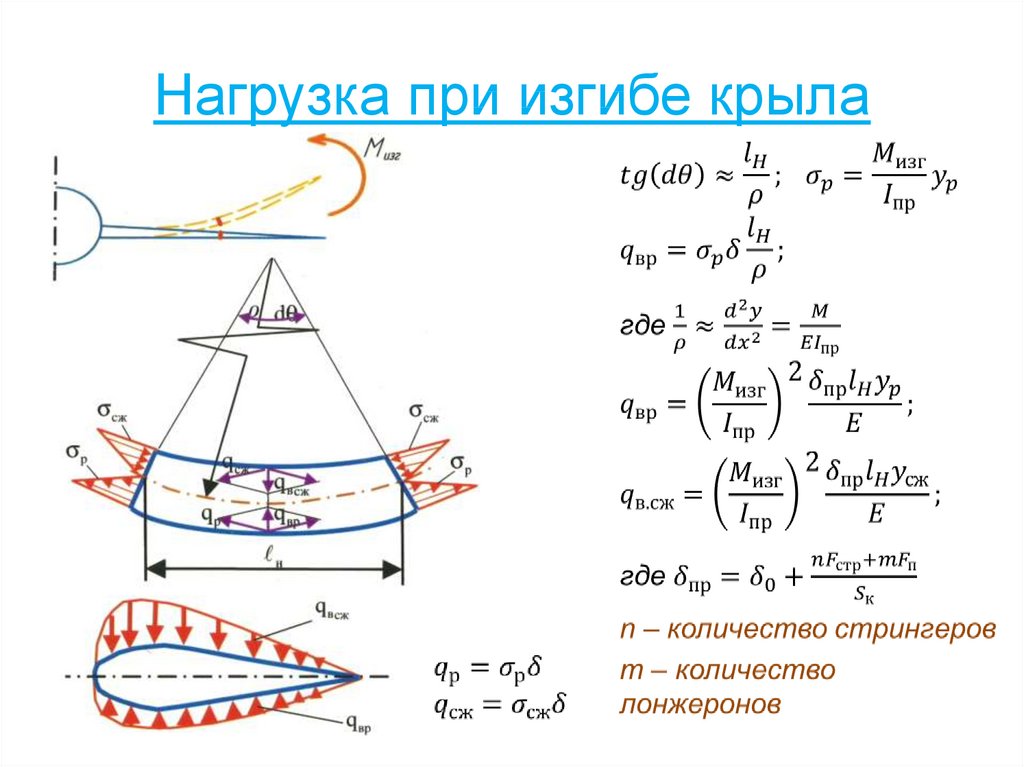
83. Нагрузка при изгибе крыла
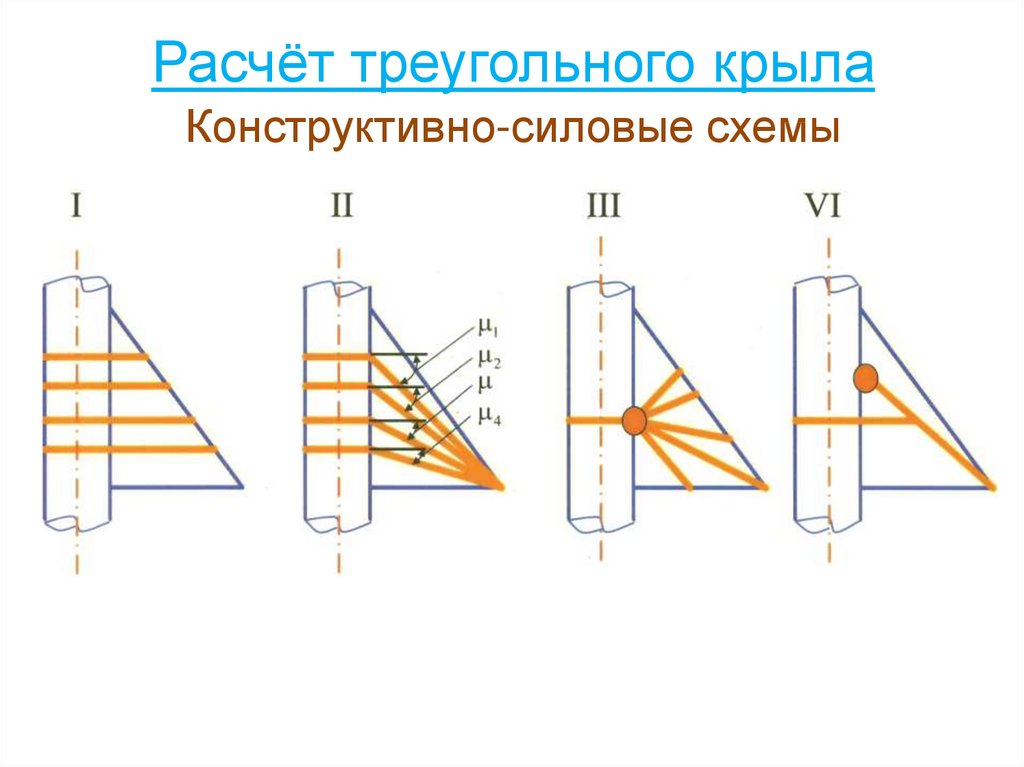
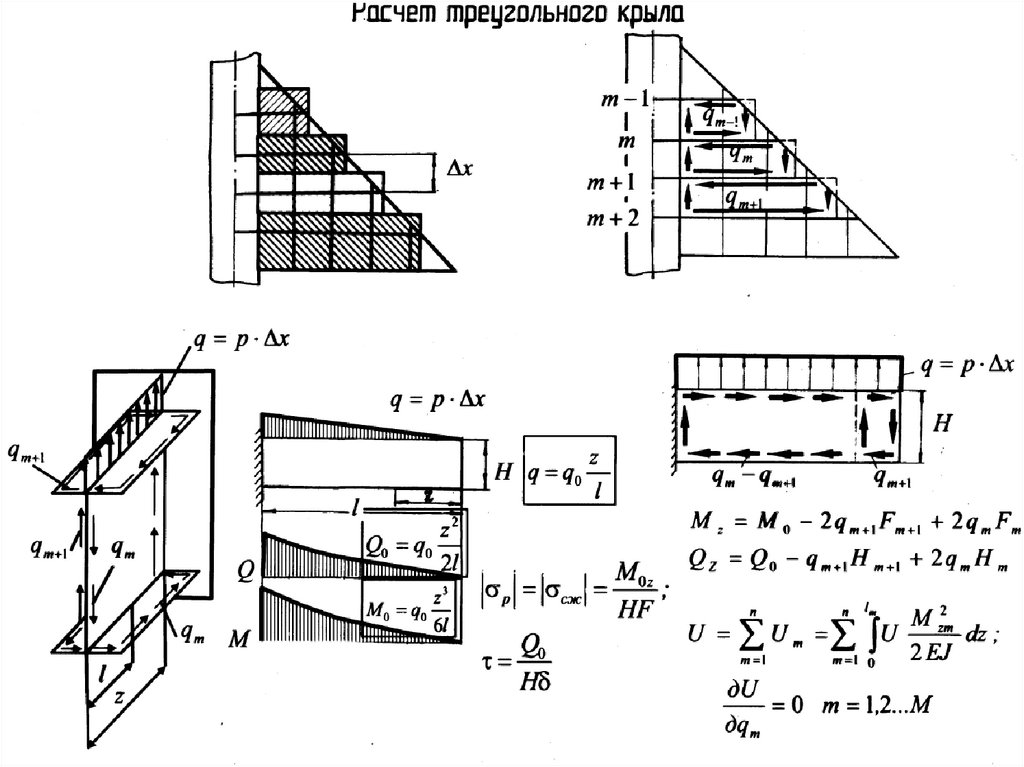
84. Расчёт треугольного крыла
Конструктивно-силовые схемы85.
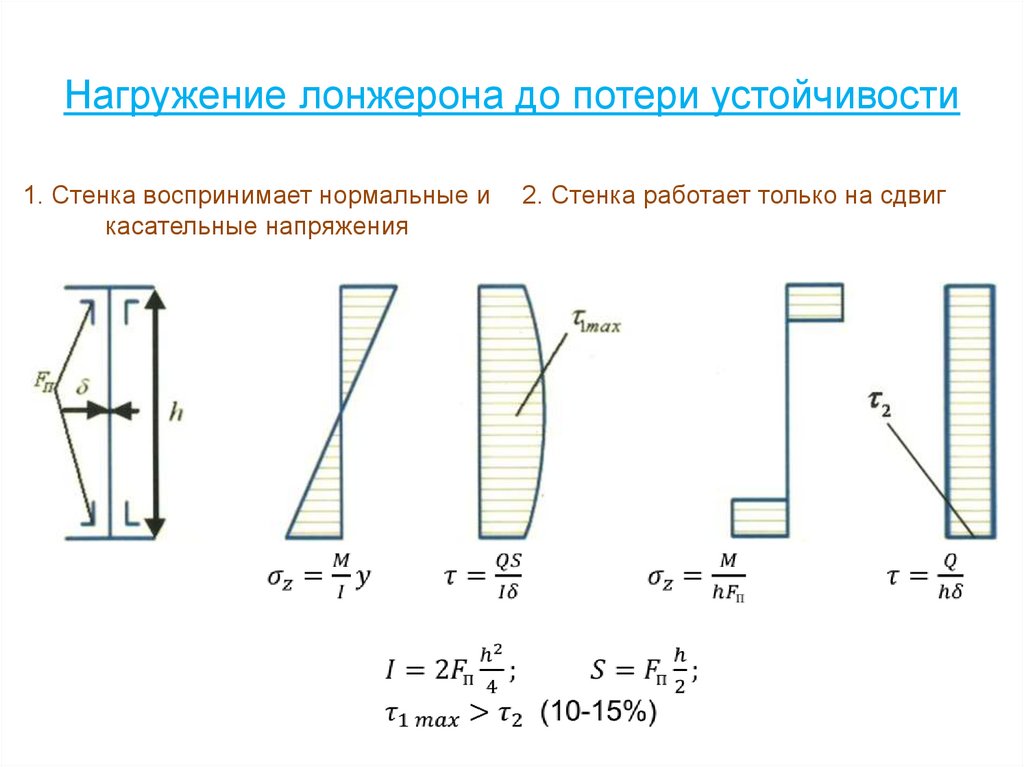
86. Нагружение лонжерона до потери устойчивости
1. Стенка воспринимает нормальные икасательные напряжения
2. Стенка работает только на сдвиг
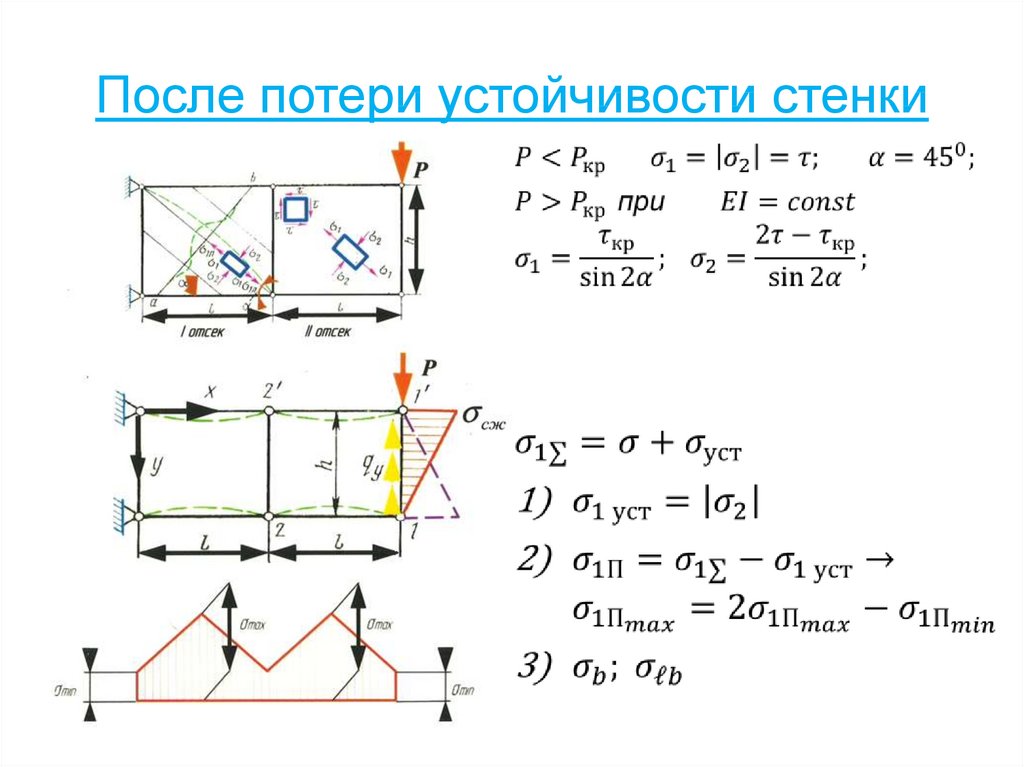
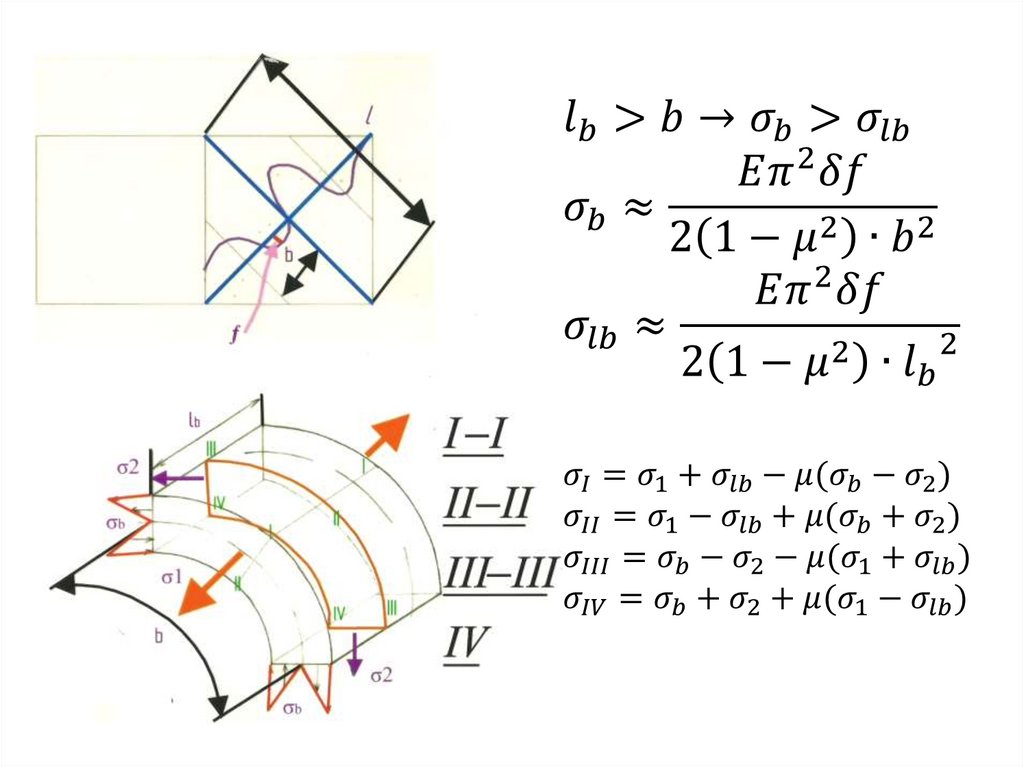
87. После потери устойчивости стенки
88.
89.
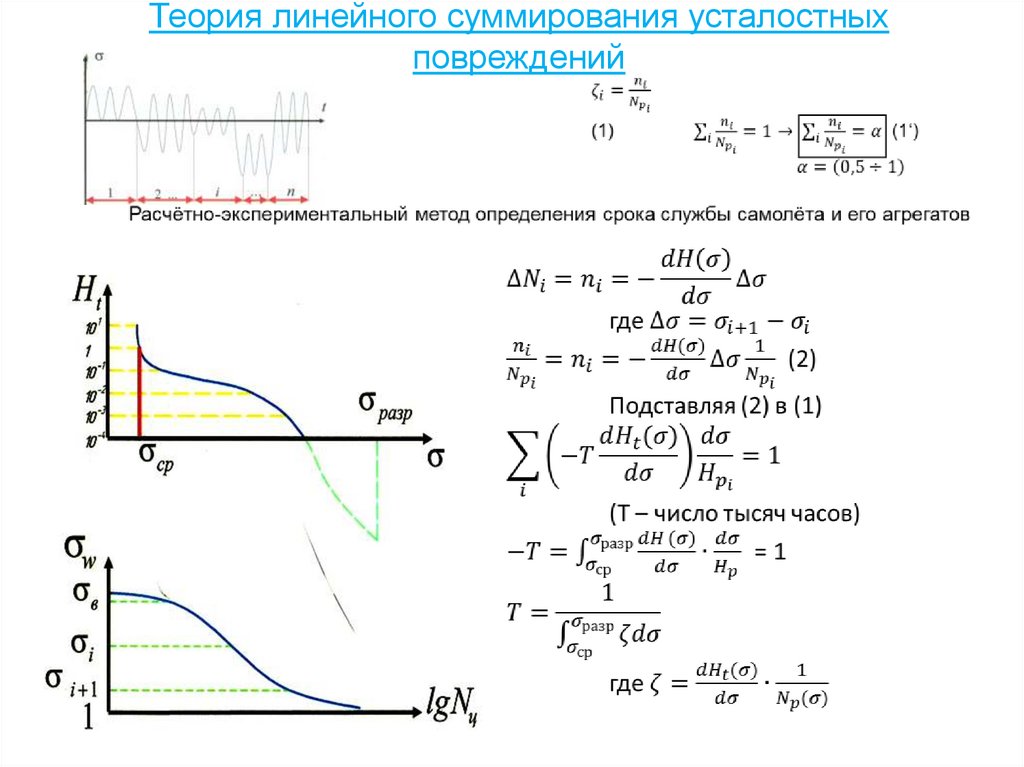
90. Усталостная прочность и определение срока службы самолёта
91. Теория линейного суммирования усталостных повреждений
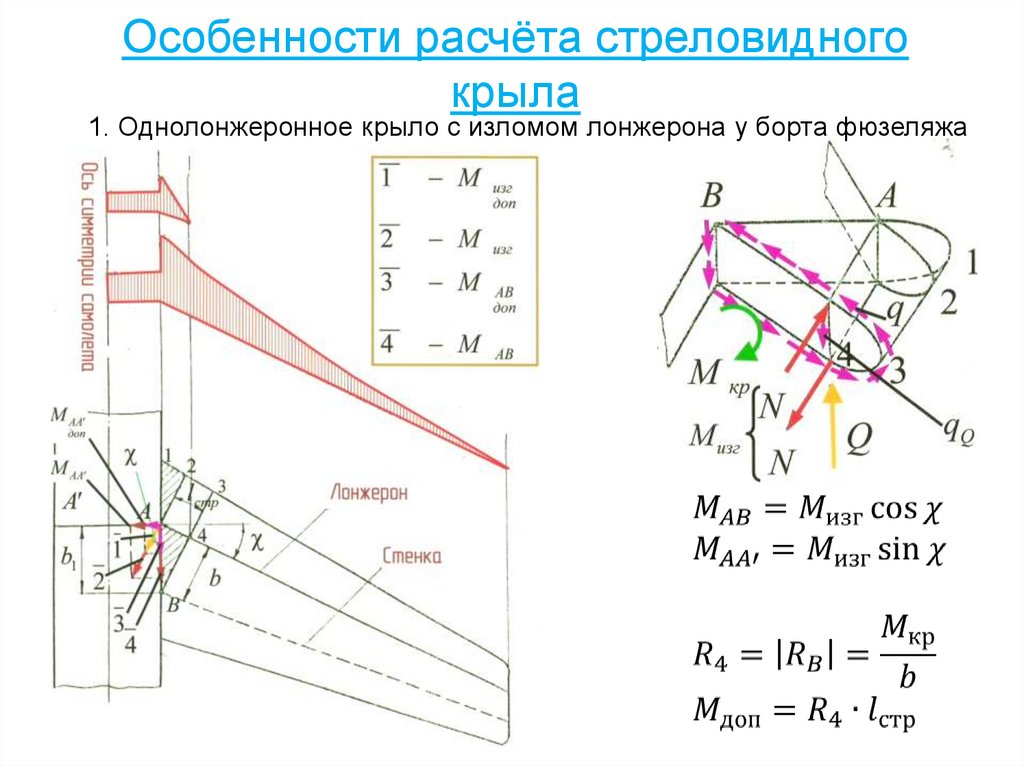
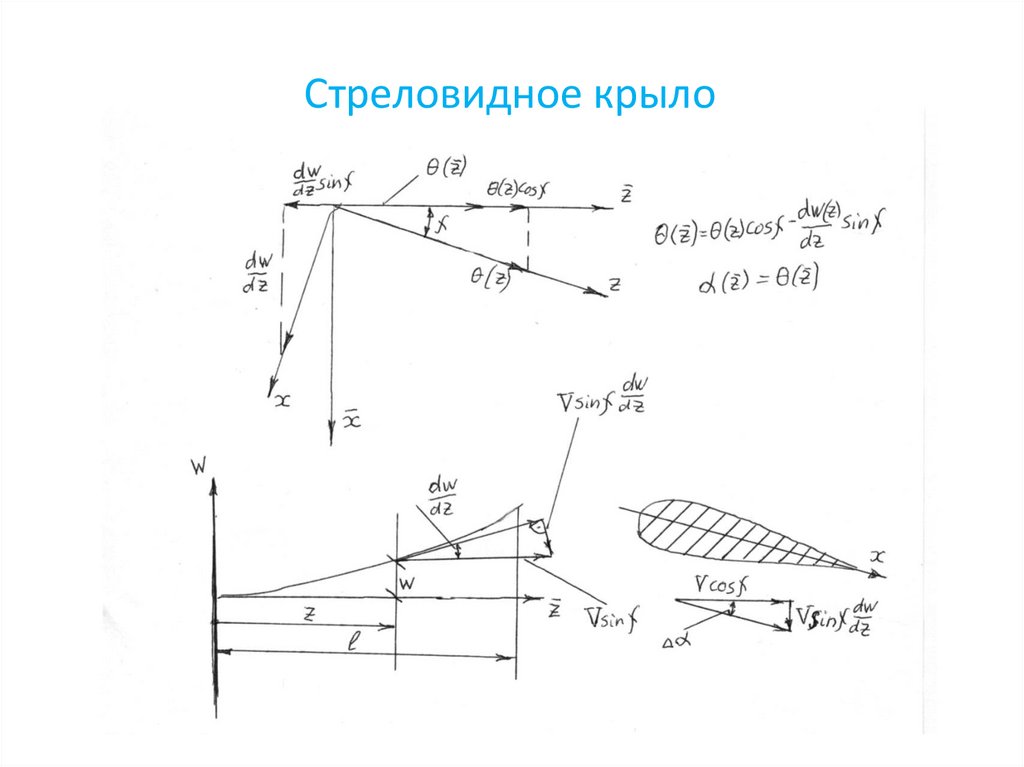
92. Особенности расчёта стреловидного крыла
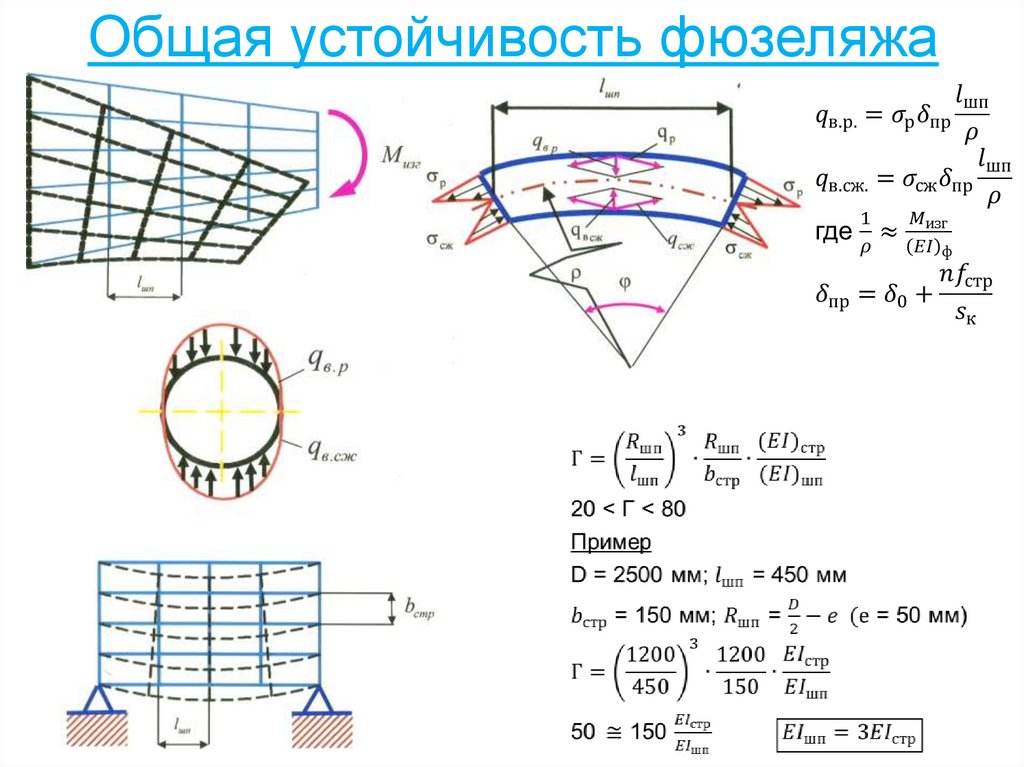
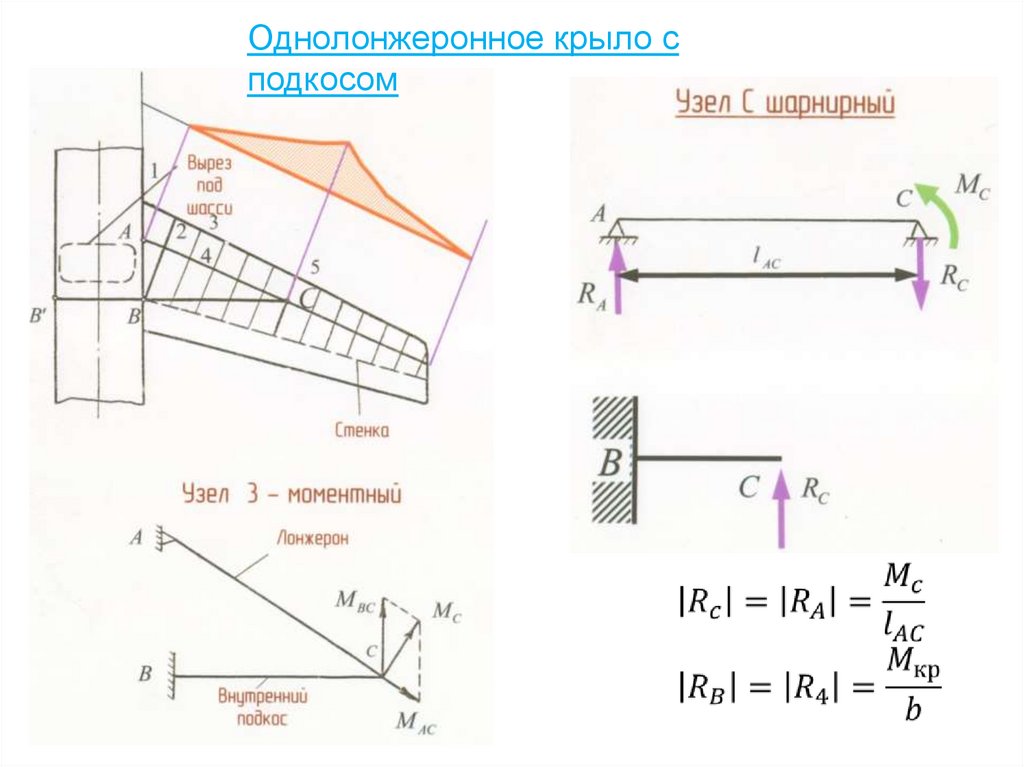
1. Однолонжеронное крыло с изломом лонжерона у борта фюзеляжа93. Общая устойчивость фюзеляжа
94.
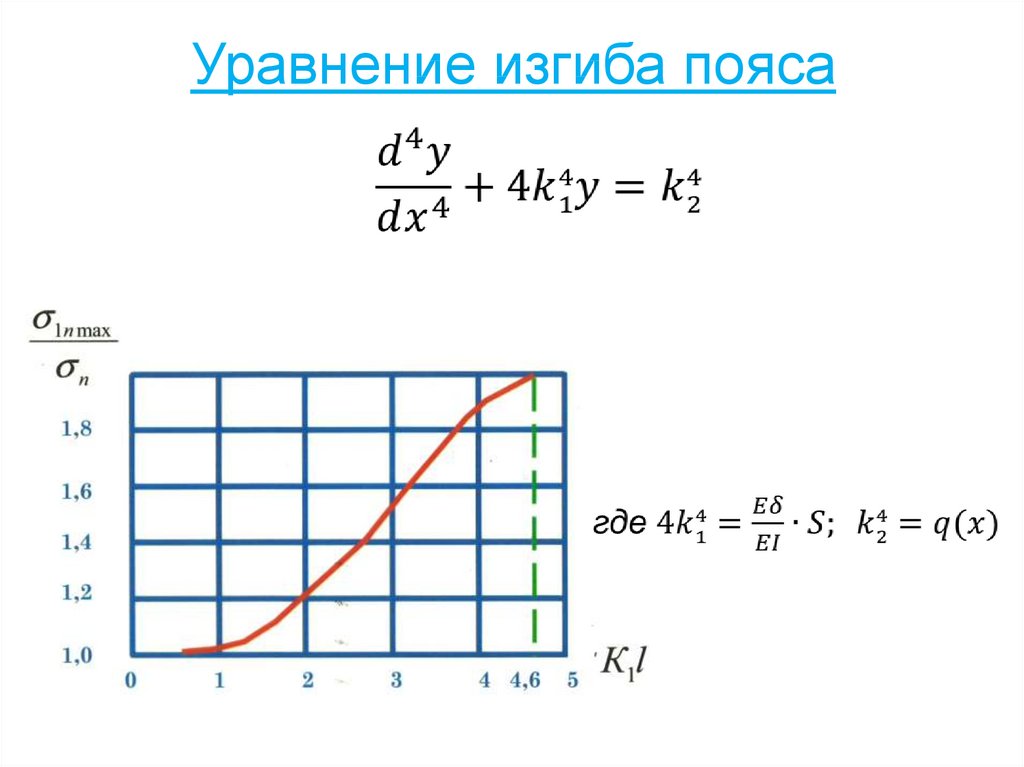
95. Уравнение изгиба пояса
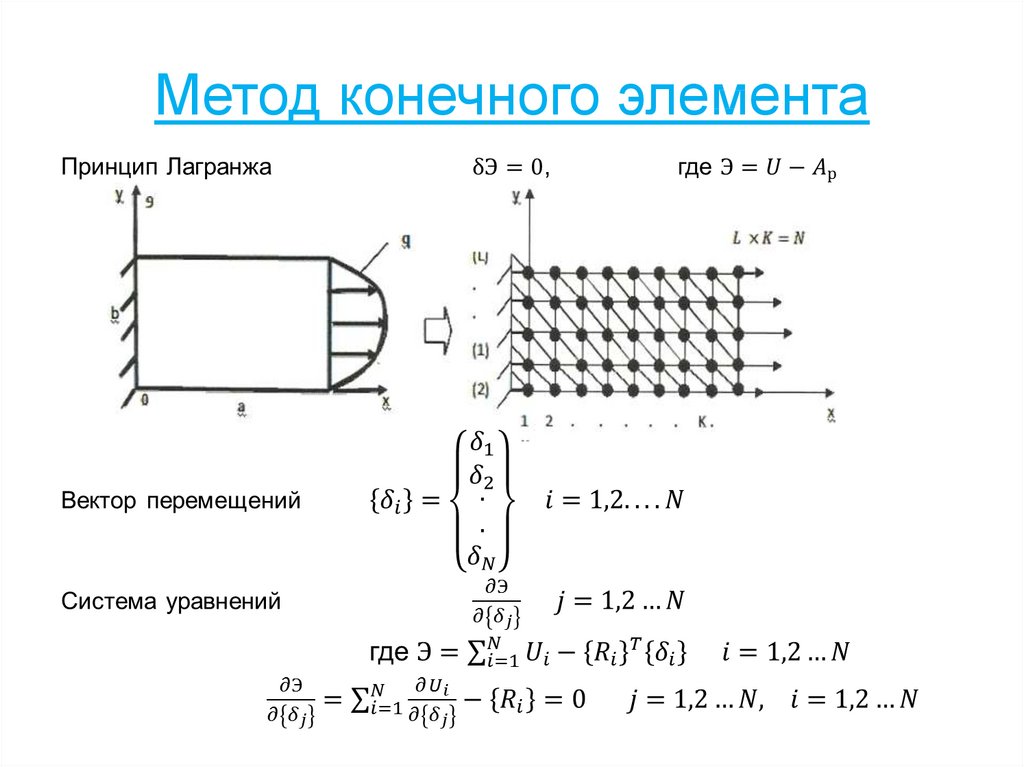
96. Метод конечного элемента
97. типы конечных элементов
98. Метод конечного элемента
99. Соотношение теории упругости в матричной форме
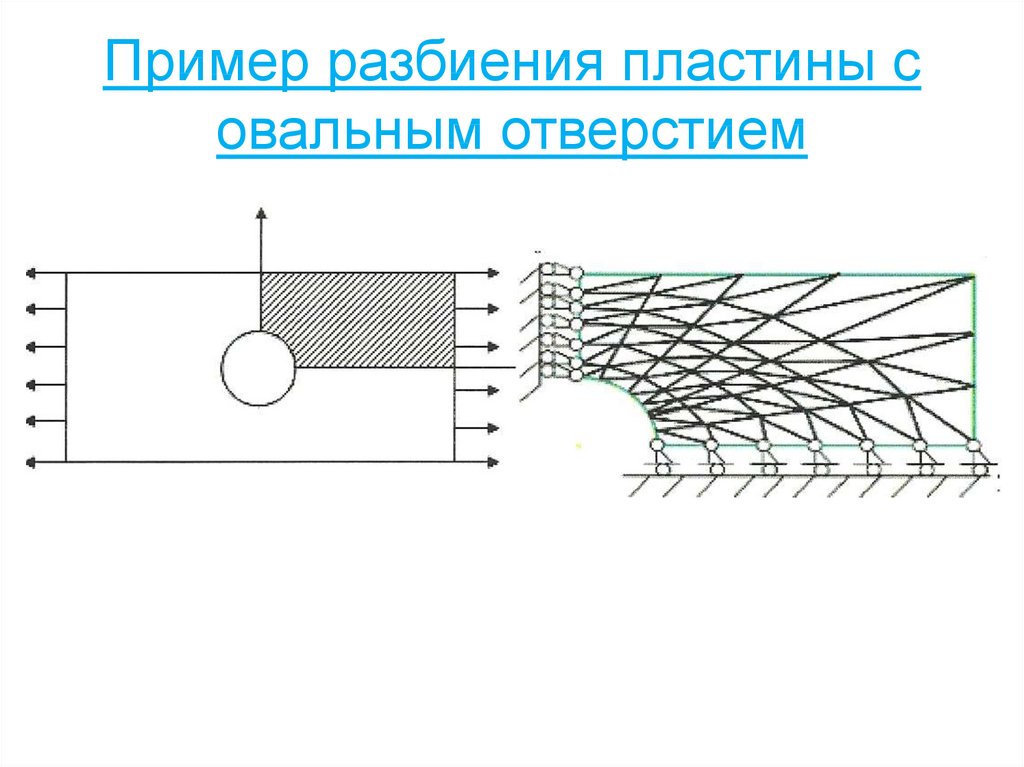
100. Пример разбиения пластины с овальным отверстием
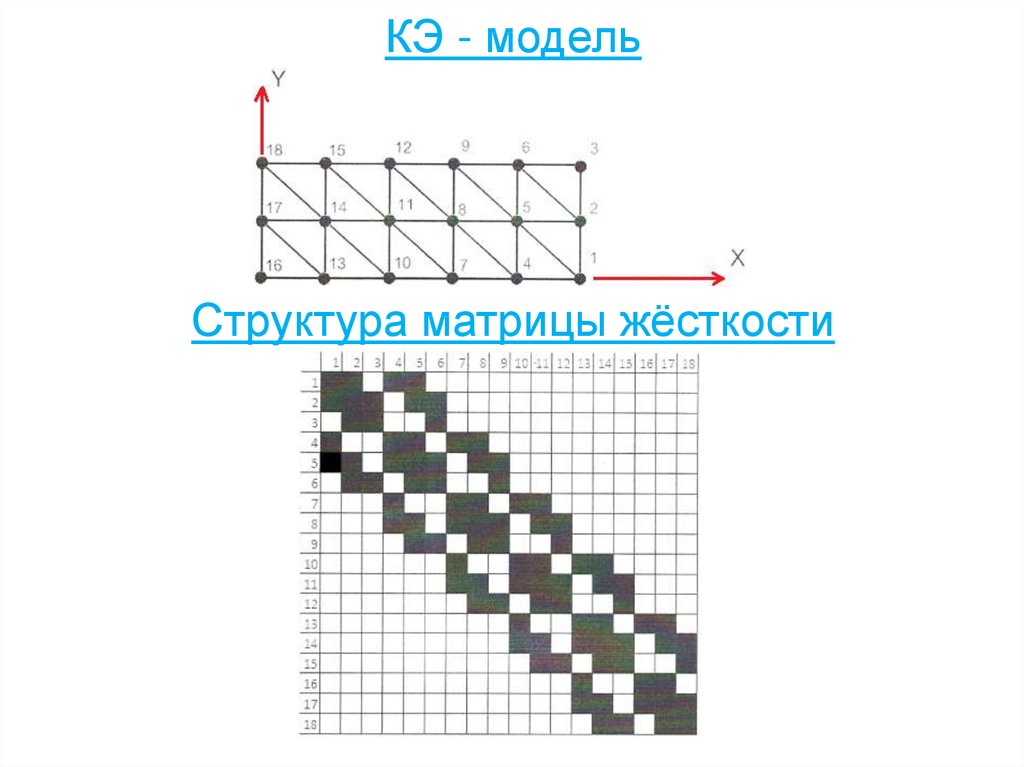
101. КЭ - модель
Структура матрицы жёсткости102.
103.
104. Примеры КЭ-моделей
105. Результаты расчёта МКЭ
106.
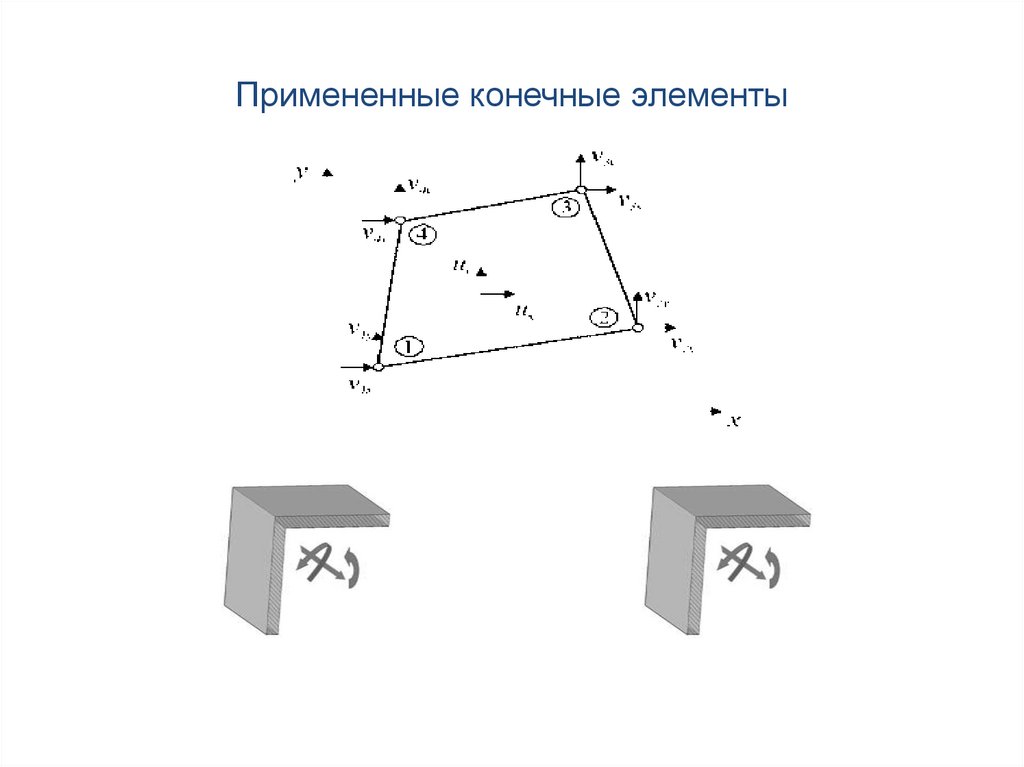
107. Примененные конечные элементы
108.
109.
110.
111.
112.
113.
Однолонжеронное крыло сподкосом
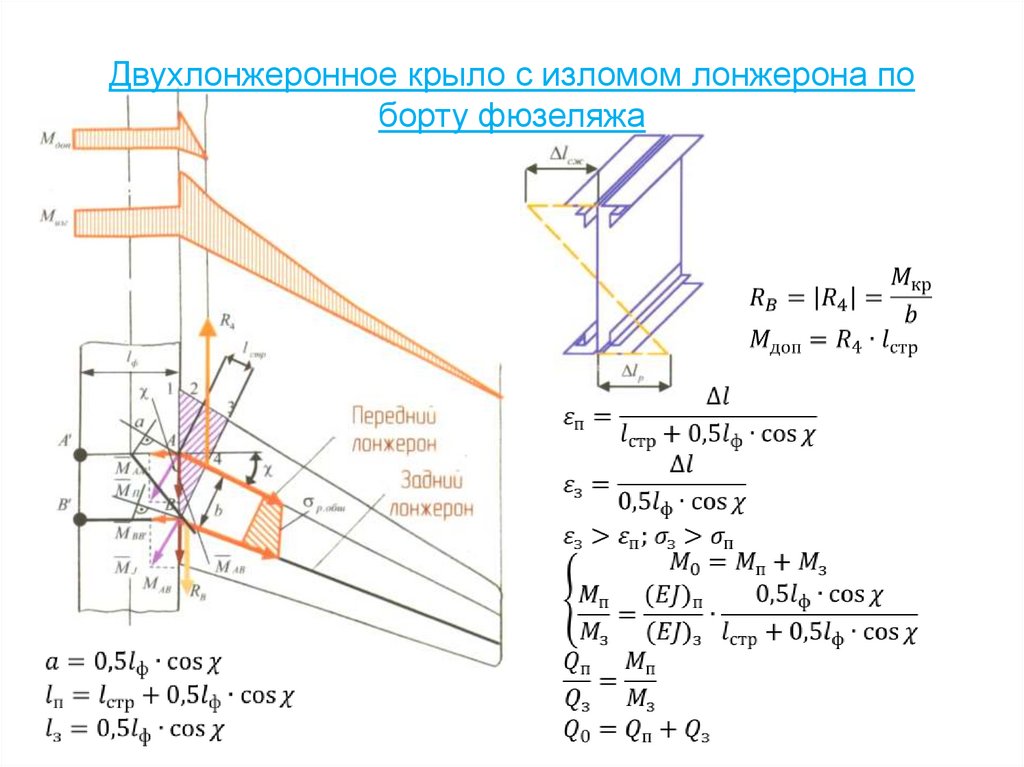
114. Двухлонжеронное крыло с изломом лонжерона по борту фюзеляжа
115.
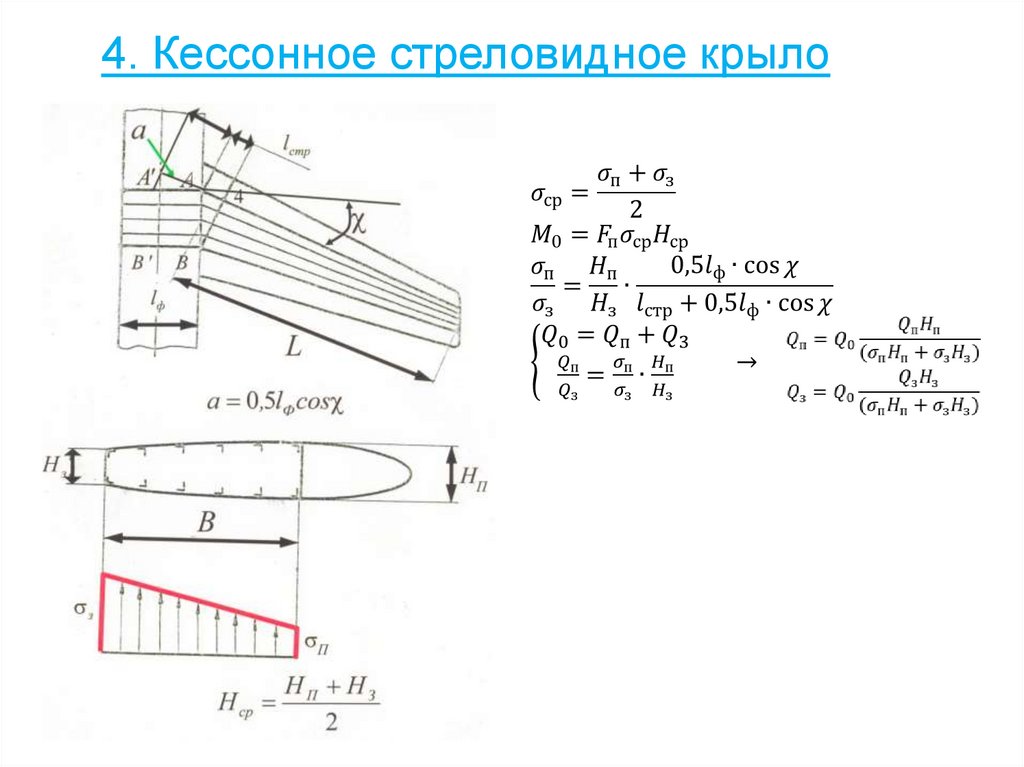
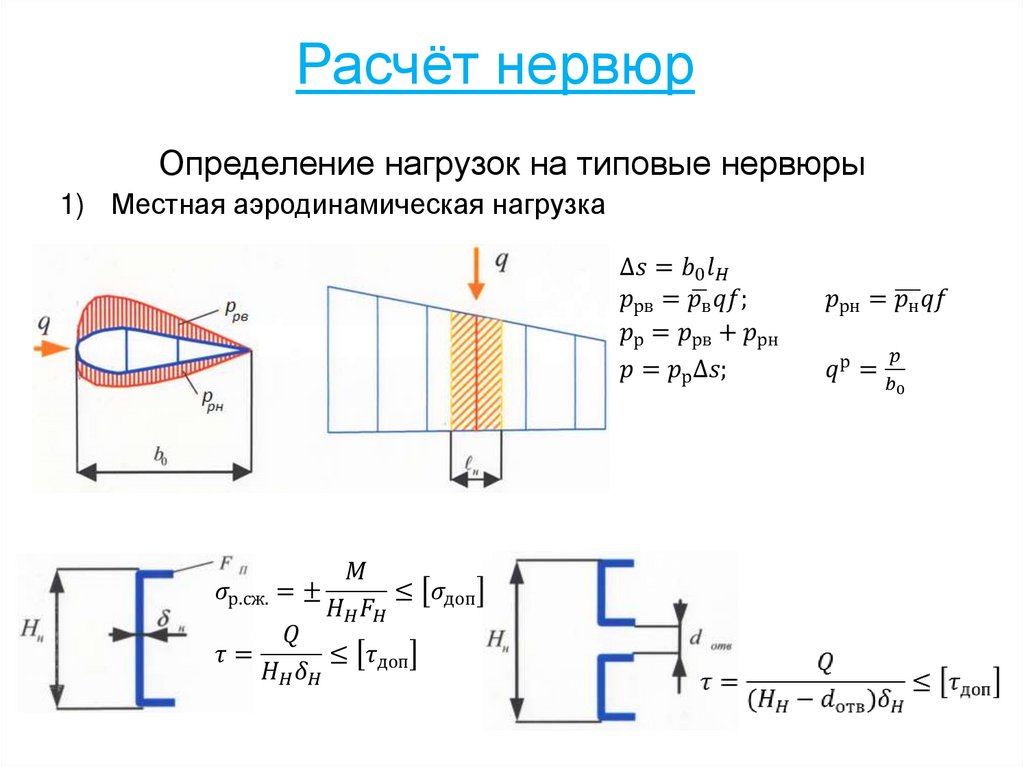
4. Кессонное стреловидное крыло116. Расчёт нервюр
Определение нагрузок на типовые нервюры1) Местная аэродинамическая нагрузка
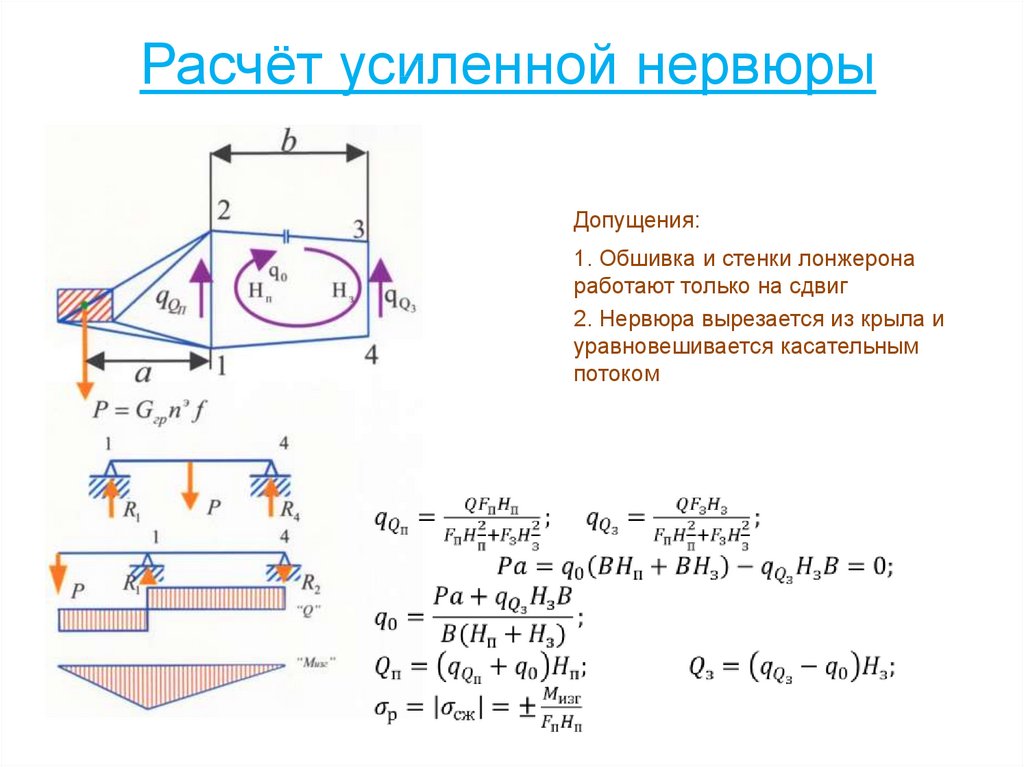
117. Расчёт усиленной нервюры
Допущения:1. Обшивка и стенки лонжерона
работают только на сдвиг
2. Нервюра вырезается из крыла и
уравновешивается касательным
потоком
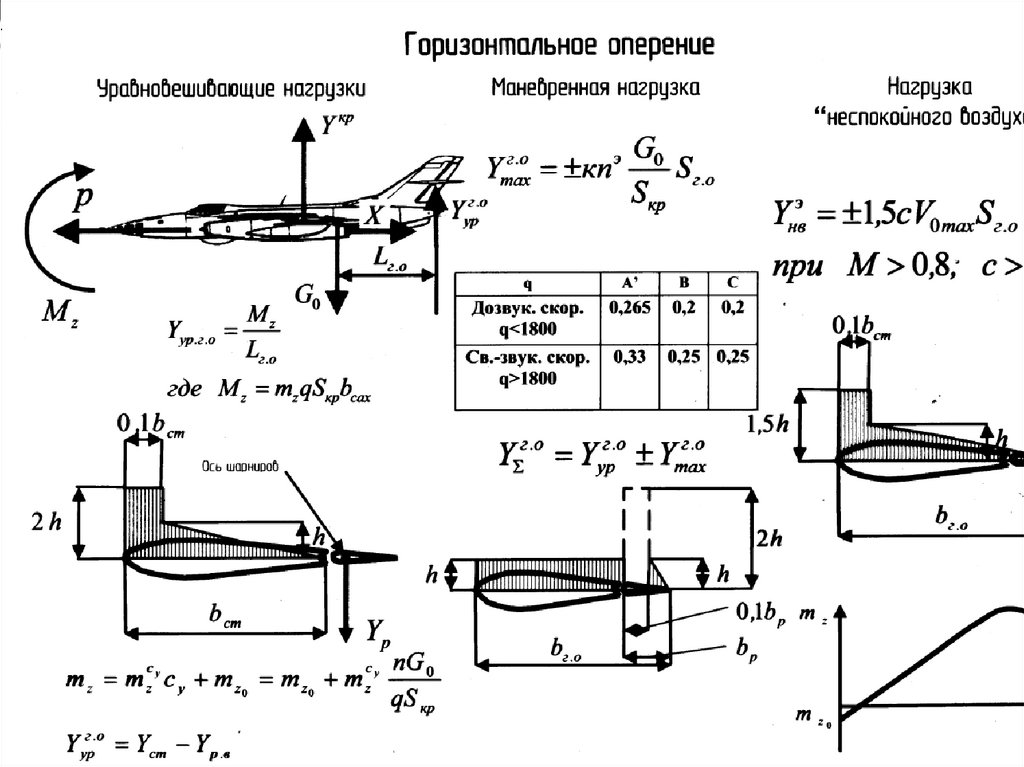
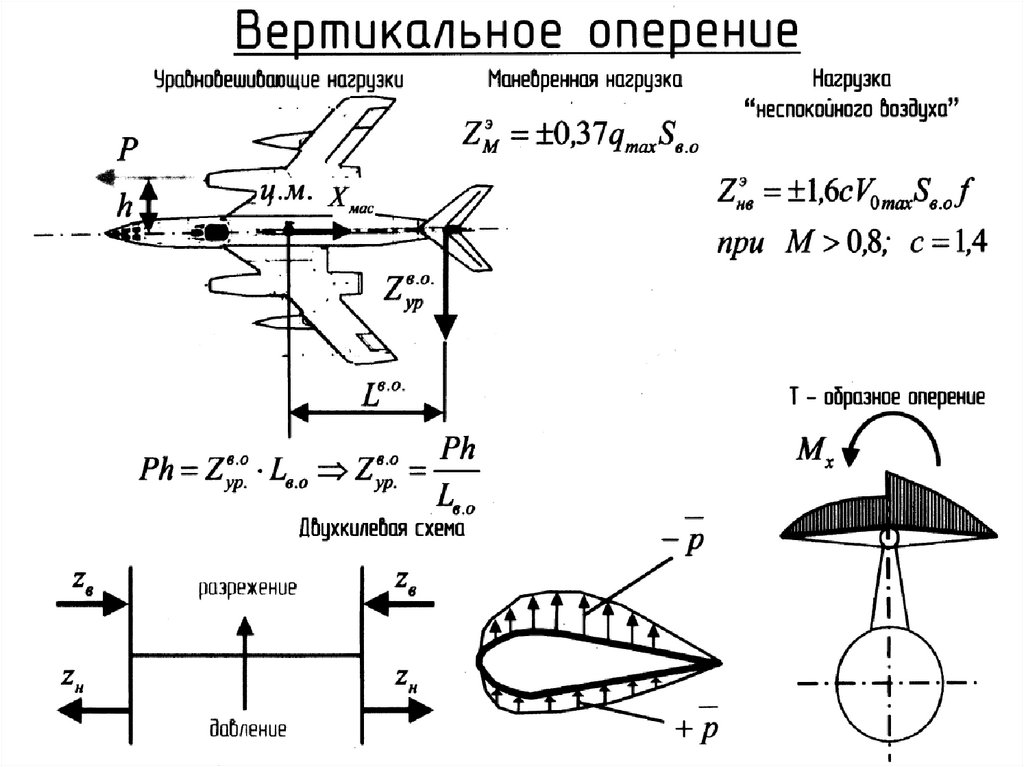
118. Внешние нагрузки, действующие на хвостовое оперение
119. Изгибно-крутильный флаттер крыла
120. Механизм возникновения
121.
122.
123.
2 y2 2 y
2
1 y
EI
m
b
qbc
y
0
2
2
2
2
z z
t
V t
t
y 2 2 Jm
1 y
2
GJ
m
b
b
qb
ec
y
2
0
2
z
z
m t
V t
t
2
2
(4)
Y z, t Af ( z )ei t
(5)
( z, t ) B ( z )ei t
(6)
z x iy;
iz
e
cos
z
i
sin
z
;
Граничные условия:
в заделке
f (0) f ' (0) (0) 0
(7)
на конце
f '' l f ''' l ' l 0
(8)
124.
Ji
B GJ ' ' m 2 A bf B m qb 2ec y B Af 0
m
V
или
A EIf " " m 2 f qbc y i
V
A bm 2 f qb2ec y i
V
f B bm 2 qbc y 0
(9)
f B GJ ' ' J m 2 qb 2ec y 0
A a11 c11 2 i d11V B c12 2 b12V 2 0
A c21 i d 21V B a22 c22 b22V
2
2
2
(10)
0
где
l
l
l
1
a11 EIf " " fdz; a22 DJ ' ' dz; b12 c y b fdz;
2
0
0
0
l
l
l
1
b22 c y b2e 2dz; c11 mf 2dz; c12 b m fdz c21;
2
0
0
0
l
l
l
1
1
c22 J m dz; d11 c y bf 2dz; d 21 c y b2ef dz;
2
2
0
0
0
2
(11)
125.
A1 4 B1 B2V 2 2 C1 C2V 2 0;2
(12)
B3 C3 C4V 0;
2
2
где
A1 c12c21 c11c22 ; B2 c11b22 c21b12 ;
B1 c11a22 a11c22 ; B3 d11c22 d 21c12 ;
(13)
C1 a11a22 ; C2 a11b21; C3 d11a22 ; C4 d11c22 b12d 21;
C3 C4V 2
;
B3
(14)
LV 4 MV 2 N 0;
(15)
2
где
L C4 B2 B3 AC
1 2 ;
M B2 B3C3 B1B3C4 B32C2 2C3C4 A1 ;
(16)
N B1B3C3 B32C1 C32 A1;
M M 2 4 LM
V
;
2L
2
(17)
126. пример
chkl cos klf z
sin kz shkz cos kz chkz;
shkl sin kl
k 1.51 ;
l
z sin
z
2l
;
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137. Дивергенция профиля без рулевой поверхности
138.
139.
140.
141.
142.
143.
144.
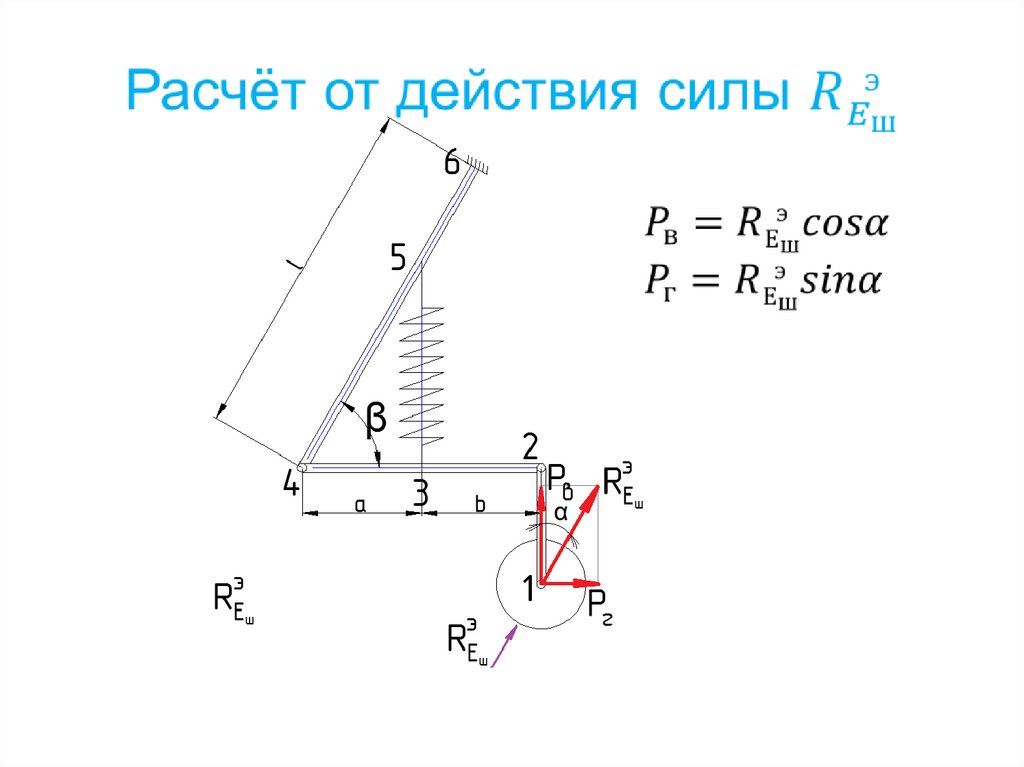
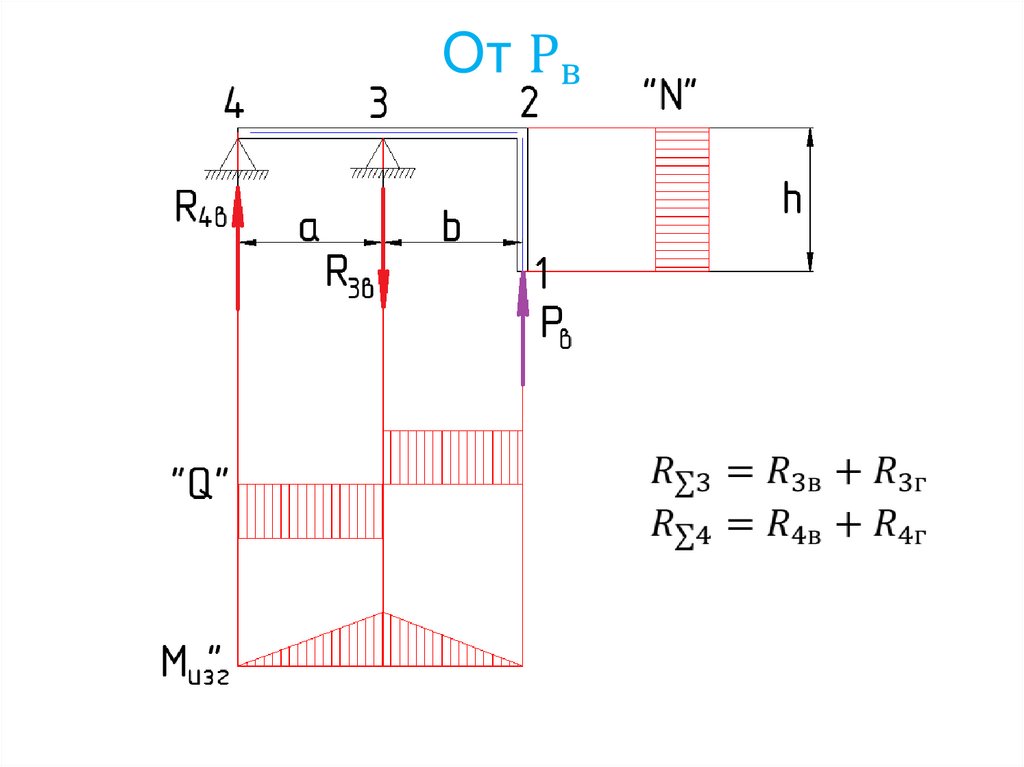
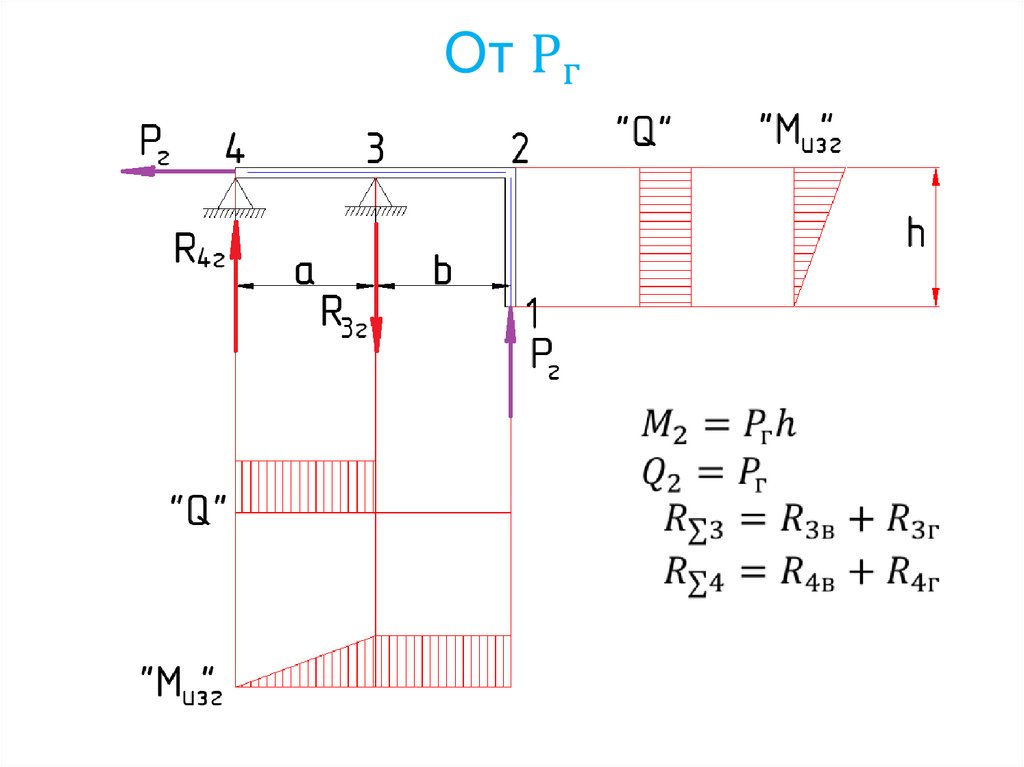
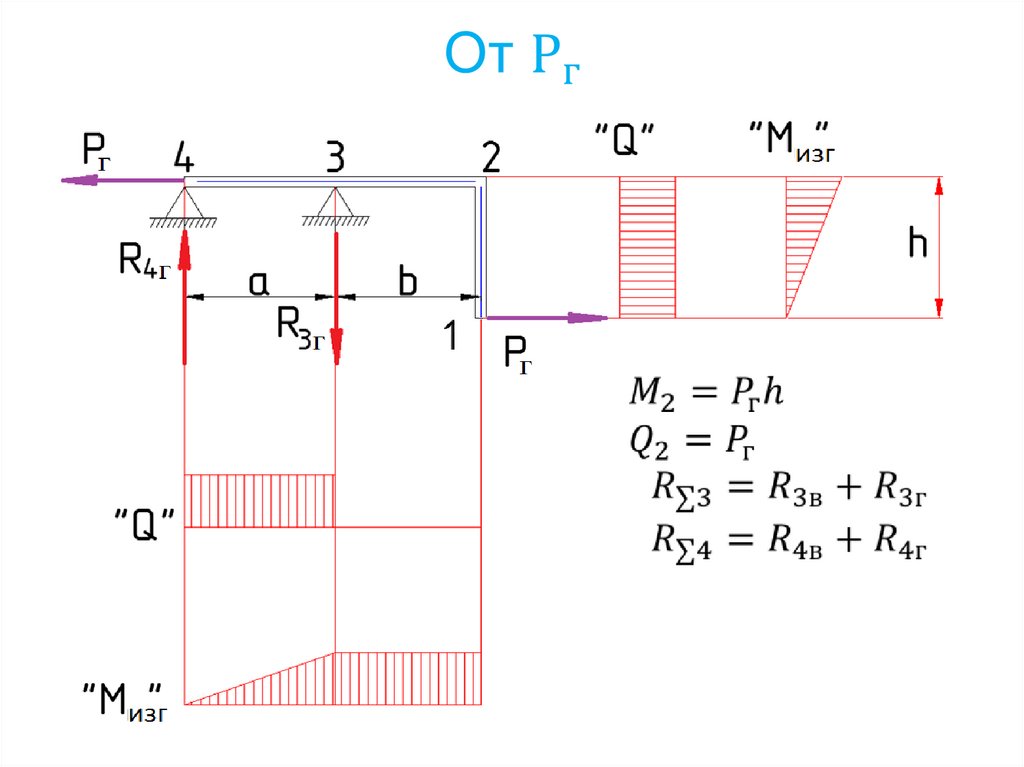
145. Расчёт от действия силы F
146.
147.
Узел 4 (узел 3 аналогично)148.
149.
150. Виды повреждений
151. Вычисление усталостного ресурса
n0 DF xNE
Dtotal jt R50%
где
n0 требуемый
усталостный
ресурс
(расчетный
срок службы),
DF – коэффициент Майнера,
x
коэффициент
уменьшения
из-за
нескольких критических мест
усталостного
разрушения,
Dtotal= ∑(n/N) – общее усталостное повреждение
( n – число приложенных циклов, N – количество
циклов до
разрушения ),
jL - коэффициент рассеивания ,
R50% - риск-фактор .
152.
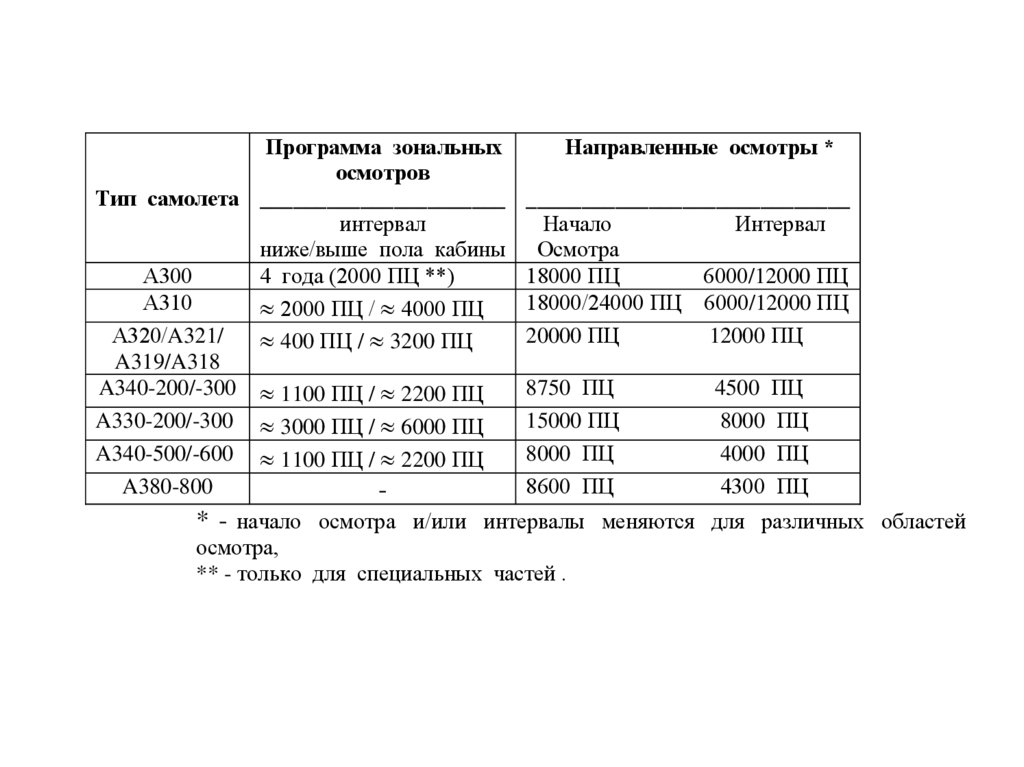
Программа зональныхосмотров
Тип самолета ______________________
интервал
ниже/выше пола кабины
А300
4 года (2000 ПЦ **)
А310
2000 ПЦ / 4000 ПЦ
А320/A321/
400 ПЦ / 3200 ПЦ
A319/A318
A340-200/-300 1100 ПЦ / 2200 ПЦ
A330-200/-300 3000 ПЦ / 6000 ПЦ
A340-500/-600 1100 ПЦ / 2200 ПЦ
A380-800
-
Направленные осмотры *
_____________________________
Начало
Интервал
Осмотра
18000 ПЦ
6000/12000 ПЦ
18000/24000 ПЦ 6000/12000 ПЦ
20000 ПЦ
12000 ПЦ
8750 ПЦ
15000 ПЦ
8000 ПЦ
8600 ПЦ
4500 ПЦ
8000 ПЦ
4000 ПЦ
4300 ПЦ
* - начало осмотра и/или интервалы меняются для различных областей
осмотра,
** - только для специальных частей .
153. Виды повреждений
154.
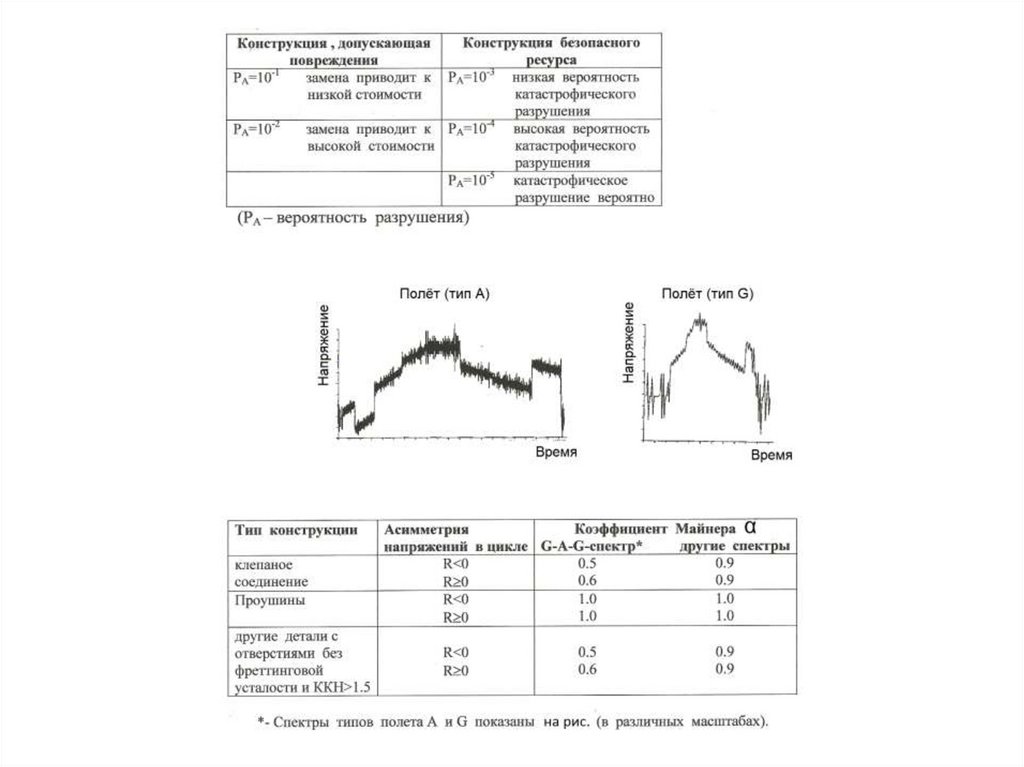
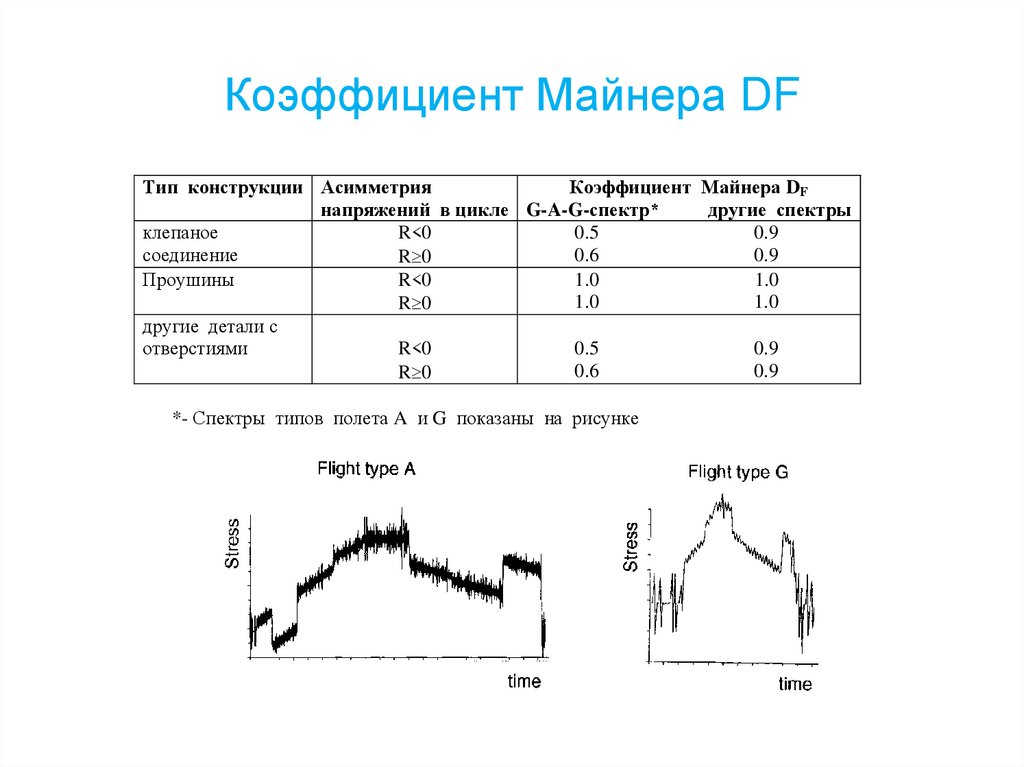
155. Коэффициент Майнера DF
Коэффициент Майнера DFТип конструкции Асимметрия
другие спектры
напряжений в цикле G-A-G-спектр*
0.9
0.5
R<0
клепаное
0.9
0.6
соединение
R 0
1.0
1.0
R<0
Проушины
1.0
1.0
R 0
другие детали с
0.9
0.5
R<0
отверстиями
0.9
0.6
R 0
*- Спектры типов полета A и G показаны на рисунке
156.
157.
158.
Многозамкнутый контуробшивки
1-ая приближённая однозамкнутая
модель
2-ая приближённая модель
(пренебрег. носком и хвостовой
частью нервюры)
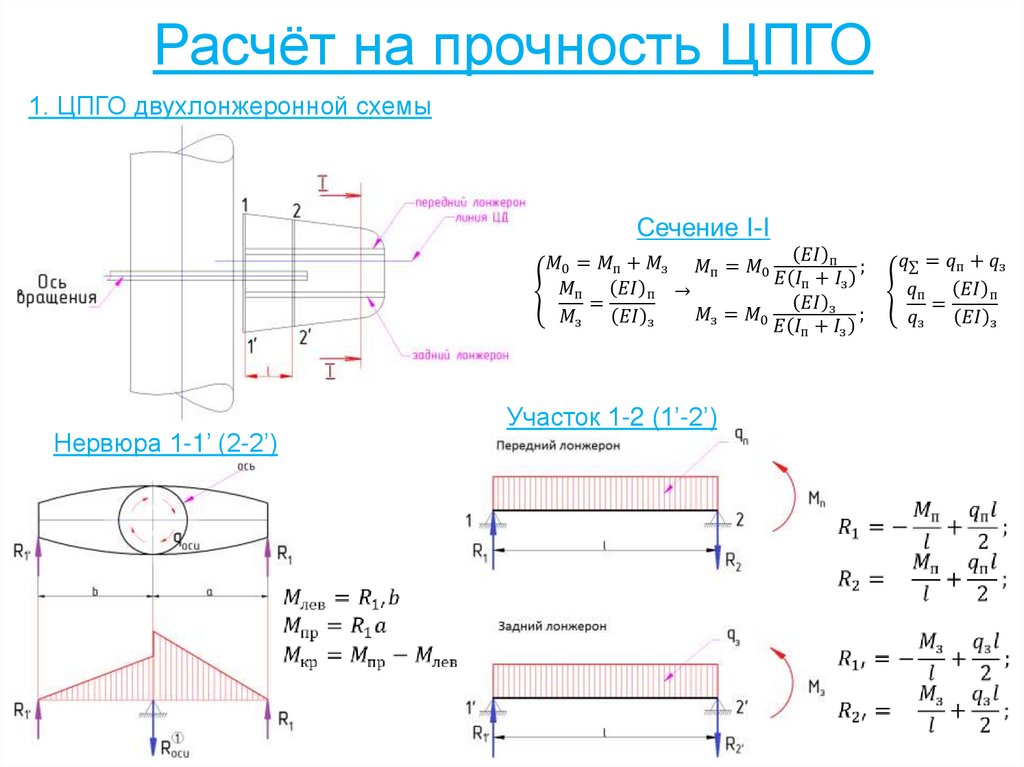
159. Расчёт на прочность ЦПГО
1. ЦПГО двухлонжеронной схемыНервюра 1-1’ (2-2’)
Участок 1-2 (1’-2’)
160.
2. ЦПГО однолонжеронной схемыЛонжерон 3-5-6
Нервюра 2-5
161. Расчёт цилиндрической оболочки под действием изб. Давления по безмоментной теории
162. Определение избыточного внутреннего давления
163.
164.
165.
166.
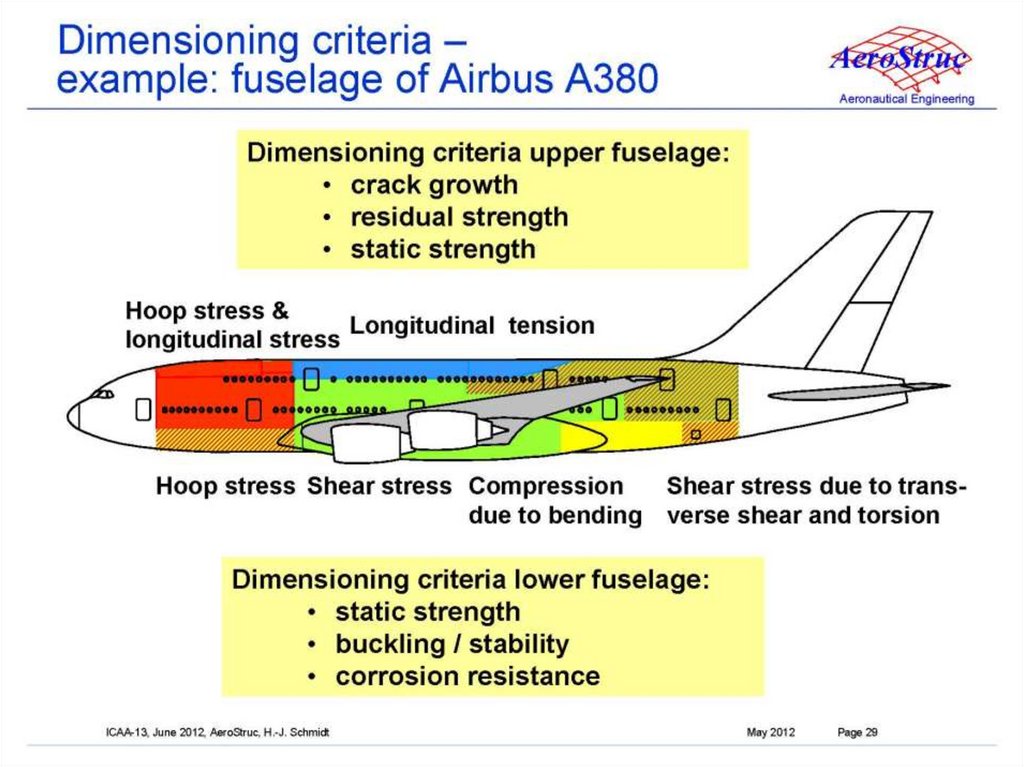
Расчет фюзеляжа в зоне выреза.При изгибе
=
δприв = δобш+ fстр∙ϕk /b
(3)
167.
Расчет фюзеляжа в зоне выреза.При изгибе
I0z = πR3 δприв
Ϭxmax = Mизг/ πR2 δприв
168.
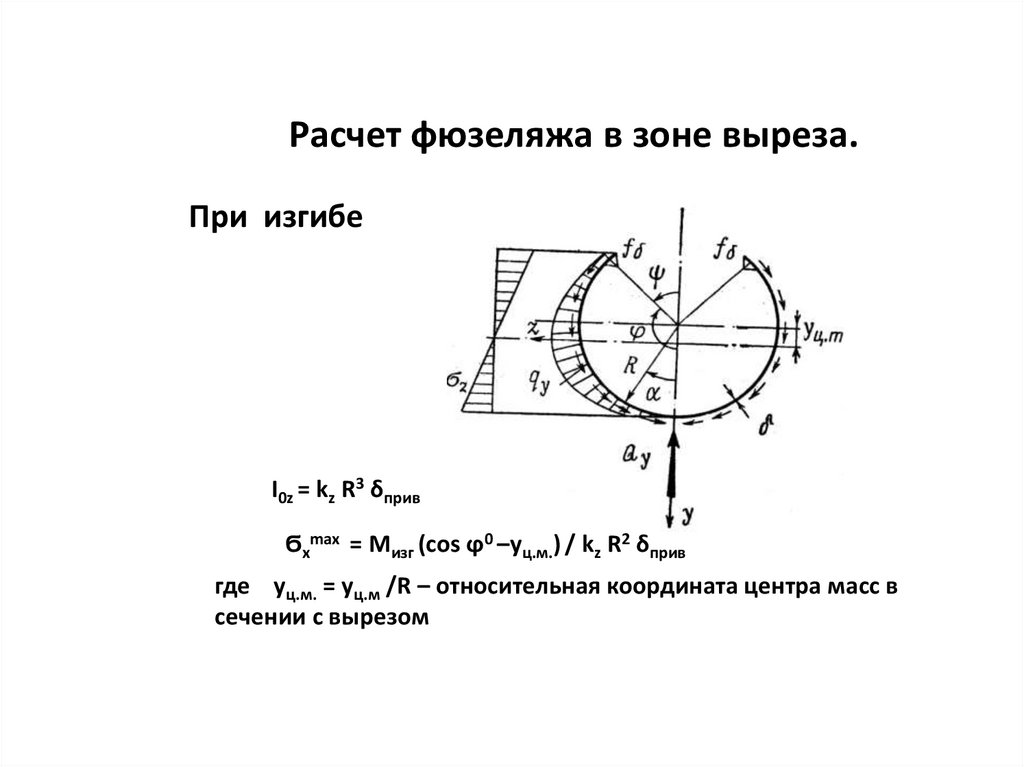
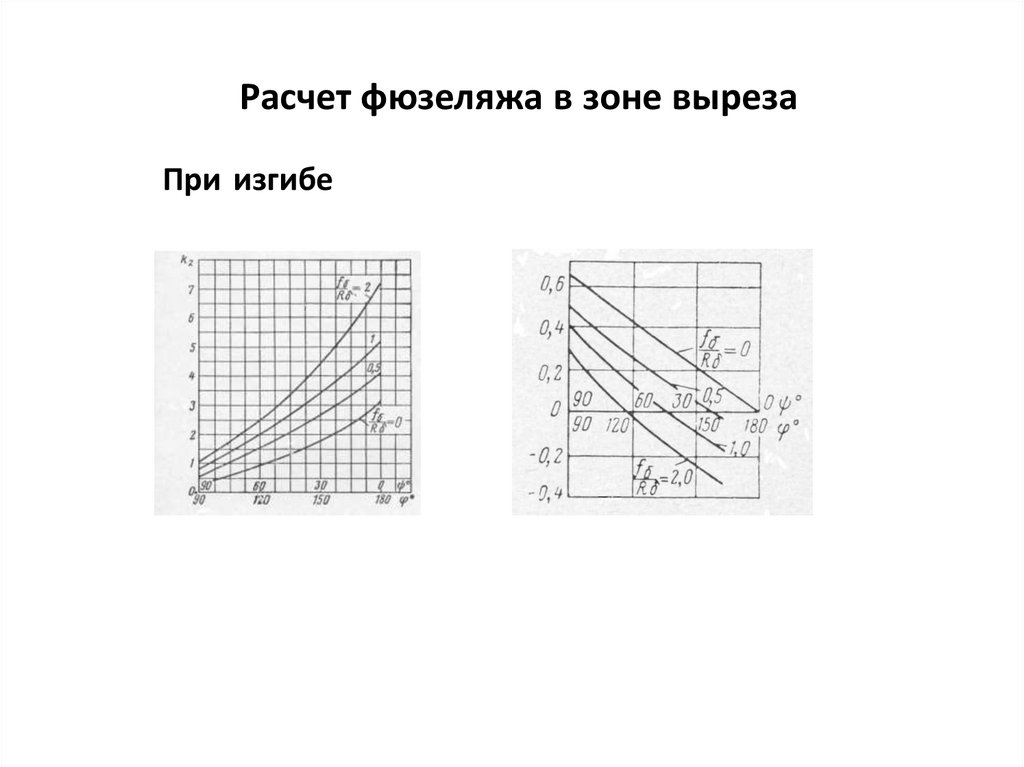
Расчет фюзеляжа в зоне выреза.При изгибе
I0z = kz R3 δприв
Ϭxmax = Mизг (cos ϕ0 –yц.м.) / kz R2 δприв
где yц.м. = yц.м /R – относительная координата центра масс в
сечении с вырезом
169.
Расчет фюзеляжа в зоне вырезаПри изгибе
.
170.
Расчет фюзеляжа в зоне вырезаПри изгибе
.
.
ϕ = (Ϭ1/ Ϭсж)∙[( h1 -y)/ (h1 – y1)]∙( h2/y)
Ϭx =ϕ∙ Mизг (y-y0) /I0z
(4)
ϕ = Ϭд / Ϭ ф
(5)
Ϭд = Ϭ1 ∙(h1 -y)/(h1 – y1)
(6)
Ϭф = Ϭсж ∙y/h2
(7)
ϕ = [ϬӀӀ + (ϬӀ - ϬӀӀ)∙ (h1 – y1)/ (h1 – y)]∙( h2/y)/ Ϭсж
(8)
где
ϬӀ - нормальное напряжение в
первом сечении на границе выреза,
ϬӀӀ – нормальное напряжение во
втором сечении
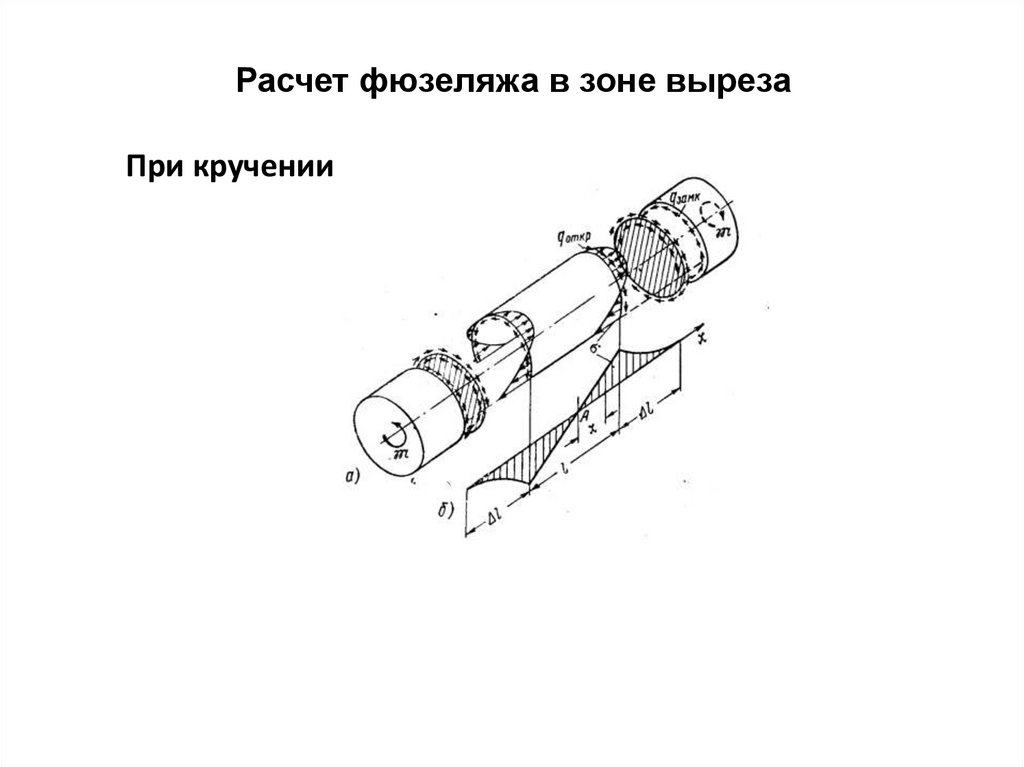
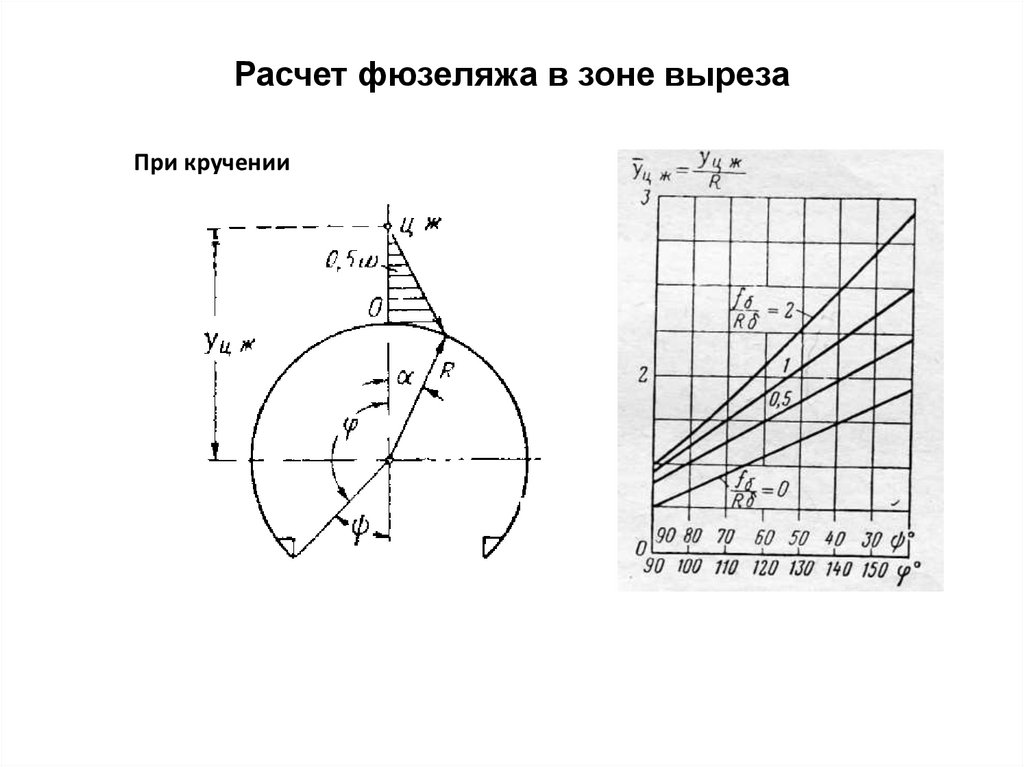
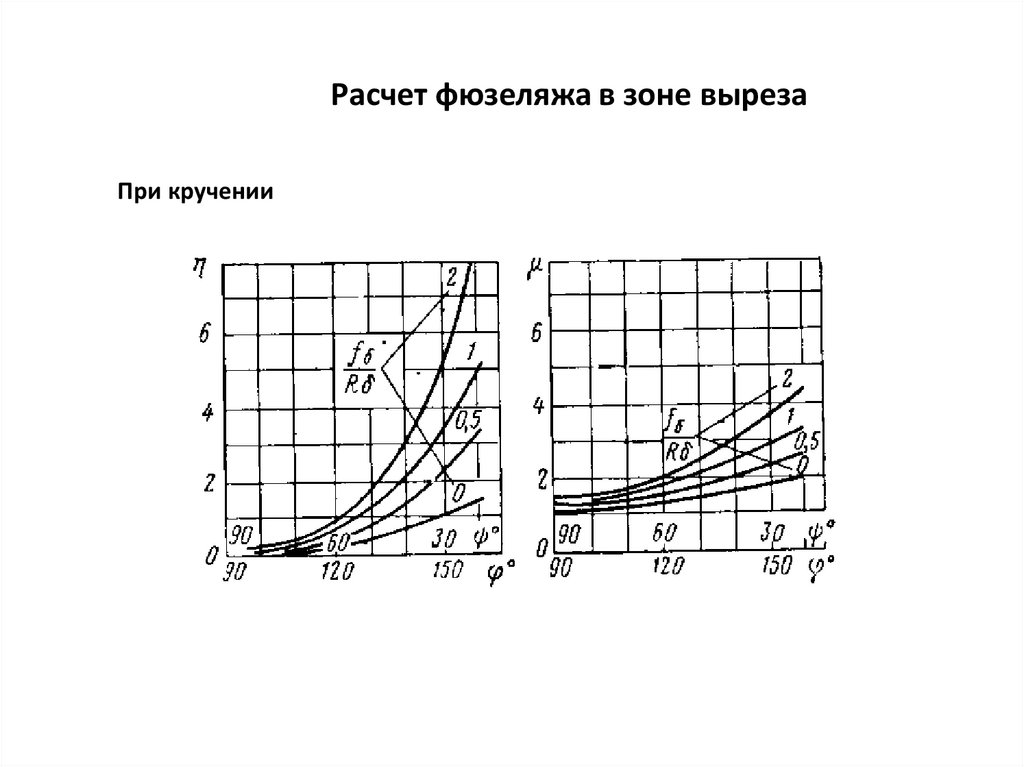
171. Расчет фюзеляжа в зоне выреза
При кручении172. Расчет фюзеляжа в зоне выреза
При кручении173.
Расчет фюзеляжа в зоне вырезаПри кручении
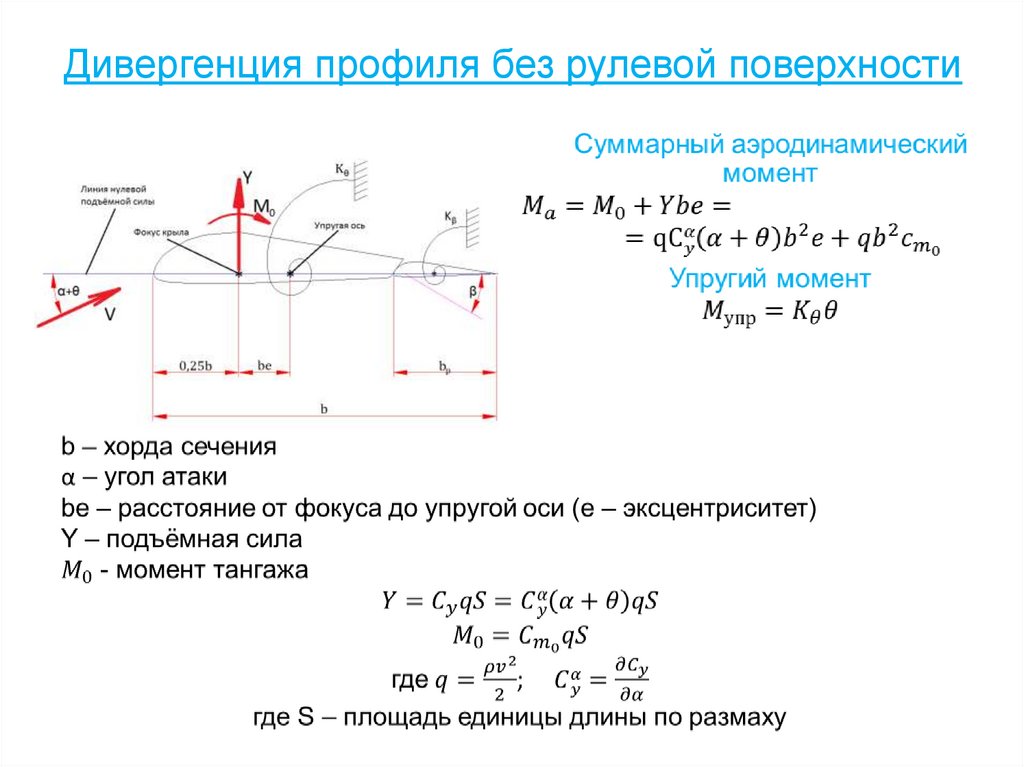
174. ДИВЕРГЕНЦИЯ ПРОФИЛЯ БЕЗ РУЛЕВОЙ ПОВЕРХНОСТИ
Y =cy q S = cyα (α+ θ) qS(1)
Mо = cmо qSb
где
(2)
q = ρV2/2 - скоростной напор ,
cy , cmо - коэффициенты подъемной силы и продольного момента ,
cyα = ∂cy/∂ α - коэффициент формы профиля ,
S – площадь единицы длины крыла по размаху.
kθ - жесткость профиля на кручение.
Суммарный аэродинамический момент относительно упругой оси
Ma = Mо + Ybe = cmо qSb2 + cyα (α+ θ) q b2 e
(3)
Упругий момент
Mупр = kθ θ
(4)
175. ДИВЕРГЕНЦИЯ ПРОФИЛЯ БЕЗ РУЛЕВОЙ ПОВЕРХНОСТИ
Условие равновесияMa = Mупр
(5)
или
cmо qSb2 + cyα qb2 e = kθ θ
(6)
отсюда определяется угол закручивания θ
θ = [(cyα αe + cmо) qb2 / kθ ]/[1- cyαq b2 e/ kθ]
(7)
УСЛОВИЕ ДИВЕРГЕНЦИИ
kθ - cyαqдивb2 e = 0
отсюда
qдив = kθ/( cyαb2 e)
следовательно
Vдив = √2 kθ/(ρ cyαb2 e)
(8)
(9)
176. ДИВЕРГЕНЦИЯ ПРОФИЛЯ C РУЛЕВОЙ ПОВЕРХНОСТЬЮ
Конструкция имеет две вращательные степени свободы α и β .Аэродинамические нагрузки:
- подъемная сила Y = (cyα θ + cyββ) qb ,
(10)
- момент тангажа Mα = [(cyα θ + cyββ)e + cmββ] qb2,
(11)
- шарнирный момент Mш = (mшα θ + mшββ) qbр2
(12)
Согласно теории тонкого профиля:
αжест = β жест = cmо =0 ;
bр - хорда руля ,
β – угол упругого закручивания руля,
mш – коэффициент шарнирного момента руля,
cyβ = ∂cy/∂ β ; cmβ = ∂cm/∂ β ; mшα =∂mш/∂α ; mш =∂mшβ /∂ β ;
Упругие восстанавливающие моменты руля и профиля:
Mп = kθ θ
(13)
Mр = kβ β
(14)
177.
Пусть cyα , cyβ , mшα , mшβ , e – постоянные (не зависят от α , чисел Re и M и т.д.) .УРАВНЕНИЯ РАВНОВЕСИЯ МОМЕНТОВ относительно:
упругой оси
Mα = Mп
или
оси шарнира руля
cyα θ + cyββ + cmββ/e = kθ θ/(qb2 e)
(15)
Mш = Mр
ИЛИ
mшα θ + mшββ = kβ β/( qbР2)
(16)
(15) + (16) – однородная система уравнений с неизвестными θ и β .
Условие существования нетривиального решения – равенство нулю определителя системы.
178.
Частные случаи:1. Упругий руль на жестком профиле (kθ →∞ и θ = 0)
из (16)
qдивр = kβ /(mшβ bР2)
(17)
2. Профиль с зажатым рулем
из (9)
qдив ж = k θ /(cyαb2 e)
ОБЩИЙ СЛУЧАЙ (ПРОФИЛЬ И РУЛЬ - УПРУГИЕ)
ж
│ cyα (1 - qдив / qдив)
(cyβ + cmβ/e )
│
D = │
│ mшα
│ =0
р
mшβ (1 - qдив /qдив) │
где qдив – скоростной напор дивергенции системы «профиль-руль»
(18)
179.
Раскрываем определительж
р
cyα (1 - qдив / qдив) mшβ(1 - qдив /qдив) - mшα (cyβ + cmβ/e ) = 0
(19)
или
ж
р
(qдив - qдив ) (qдив - qдив ) - mшα (cyβ + cmβ/e )/[(cyβ + cmβ/e ) qдив2] = 0
μ = mшα (cyβ + cmβ/e )/( mшβ cyα)
Обозначим
(20)
(21)
(20) принимает вид :
(1 - μ) qдив2 – (qдив ж + qдив р) qдив + qдив ж qдив р = 0
(22)
Два корня уравнения соответствуют двум значениям критической скорости дивергенции:
qдив = (qдив ж + qдив р)/[2(1 - μ)] ± √[(qдив ж - qдив р)2 +4 μ qдив ж qдив р]/[2(1 - μ)] (23)
180.
qдив = qдив ж(1 - │μ│/(1+│ qдив р │/ qдив ж))μ<0
(24)
Эффект рулевой поверхности (появление доп. степени свободы) сказывается на снижении qдив.
μ > 0 – обратная картина ,
Анализируя вышеизложенное отметим, что если контур управления рулевой поверхностью обладает
р
большой жесткостью (kβ →∞, qдив → 0 ), то скоростной напор дивергенции, согласно (22) можно
представить, как
qдив = qдив ж/(1- |μ|)
(25)
μ = 0 – наличие руля не оказывает влияния на qдив , → qдив = qдив
ж
181.
ДИВЕРГЕНЦИЯ ОДНОМЕРНЫХ УПРУГИХ КОНСТРУКЦИЙПРЯМОЕ КРЫЛО
Рассмотрим крыло конечного размаха с упругой осью,
перпендикулярной продольной оси самолета. Все
характеристики крыла есть функции координаты z .
Пусть аэродинамическое воздействие потока на крыло сводится только к подъемной силе Y, приложенной
по линии фокусов и определяемой только упругим закручиванием крыла на угол θ(z).
Вырежем элемент крыла единичной длины по размаху и запишем для него дифференциальное уравнение
равновесия:
d/(GJ dθ/dz) dz + Ma (z) = 0
(26)
где
Ma (z) = Ybe = qдив cyαθb2 e - аэродинамический момент, приходящийся на единицу длины крыла (27).
Тогда (26) примет вид
d/dz (GJ dθ/dz) + qдив cyαθb2 e =0
Это – однородное уравнение с переменными коэффициентами.
(28)
182. ДИВЕРГЕНЦИЯ ОДНОМЕРНЫХ УПРУГИХ КОНСТРУКЦИЙ
Примем GJ = const, b = const, тогдаGJ d2 d2θ/dz2 + /dz2 + qдив cyαb2 eθ=0
(28’)
или
d2θ/dz2 + λ02 θ = 0
(28’’)
где
λ02 = qдив cyαb2 e/ GJ
(29)
Граничные условия в этом случае
θ(0) = 0 (30)
dθ(l)/dz = 0
(31)
Общее решение уравнения (28’’) имеет вид
θ(z) = C1 sin λ0z + C2 cos λ0z
(32)
183.
Из (30) и (31) получаемC2 = 0
(33)
cos λ0l = 0
(34)
Нетривиальные решения возможны при (λ0 = 0 – посторонний корень)
λ0l = (2n +1) π/2 (n = 0,1,2,…)
(35)
Таким образом, получаем бесконечную последовательность собственных значений задачи
λ02 =[(2n +1) π/2l]2 (n = 0,1,2,…)
(36)
Видим, что все собственные значения вещественные и положительные.
Приравнивая (29 и (36) получаем
qдив = (2n +1)2 π2 GJ/(4l2cyαb2 e) → V див = (2n +1) π/bl ∙√ GJ/(2ρcyα e)
(37)
184.
Если сравнивать (38) и (9), то видим, что: 1) структура формул тождественна, что говорит о том, чтомодель профиля точно отражает основные черты явления дивергенции , 2) влияние удлинения (размаха)
величину V див весьма существенно.
Собственному значению λ1 = λmin соответствует форма отклонения
θ1 (z) = C1 sin λ1z = C1 sin (π z/2l)
(39)
Это решение построено для прямого крыла (b= const), но аналитическое решение можно построить и для
трапециевидного крыла , хорда которого меняется по линейному или степенному закону. При сложном законе
изменения построить аналитическое решение очень трудно.
185.
Рассмотрим один из методов приближенного решения.Представим угол закручивания θ (z) в виде
θ (z) = θ0 f(z)
где θ0 = q0 - искомая обобщенная координата,
(40)
f(z) – заданная функция формы деформации.
Вычисляем энергию деформации при кручении
l
U = ½ ∫ GJ(dθ/dz)2 dz
(41)
0
Поскольку мы приняли GJ = const, то после подстановки (40) в (41) получаем
l
U = ½ GJ θ02 ∫ (df/dz)2 dz
0
(42)
186.
Отсюда, вариация энергии на перемещении δθ0 будетl
δU = GJ θ0 δθ0 ∫ (df/dz)2 dz
(43)
0
Определяем теперь работу внешних сил, т.е. аэродинамического момента на перемещении δθ :
l
δAP = [∫ Ma ∂θ/∂θ0 dz ] δθ0 = Q0 δθ0
(44)
0
где Q0 - обобщенная сила.
Но поскольку (согласно теории тонкого профиля)
Ma = Ybe = q cyαb2 θ (z)e
то получаем
(45)
l
δAP = q cyαb2e θ0 δθ0 ∫ f2 (z)dz = Q0 δθ0
(46)
0
и отсюда определяем обобщенную силу
l
Q0 = q
cyαb2e
θ0∫ f2 (z)/dz
0
(47)
187.
Далее, из условия равновесия системы, имеемδAP = δU
(48)
q = qдив ; V = Vдив
(49)
и
Подставляя в δAP и δU их значения, получаем
l
l
GJ θ0 δθ0∫ (df/dz)2 dz = qдив cyαb2e θ0 δθ0 ∫ f2 (z)dz
0
0
и отсюда можем определить скоростной напор дивергенции
l
l
qдив = GJ ∫ (df/dz)2 dz / cyαb2e ∫ f2 (z)dz
0
0
(50)
188.
Из (50) видно, что при заданных геометрических и аэродинамических характеристиках крыла скоростьдивергенции зависит от заданной формы деформации f(z). Для получения достаточной точности f(z) должна
удовлетворять геометрическим условиям защемления корневой части крыла
θ (z)z=0 = 0
(51)
Выполнение краевого условия на свободном конце
(df/dz) z=l = 0
(52)
Способствует повышению точности расчета, однако имеет в данной задаче второстепенное значение. (Можно
показать, что для различных форм удовлетворение условий (51) и (52) и не обязательно. При удовлетворении
граничных условий на свободном конце различие в значении Vдив не превышает 10%).
В заключении отметим, что точность определения Vдив заметно повышается с увеличением количества форм.
Так, при одном члене ряда , т.е. qдив = 3 GJ/ cyαb2e l2
при двух членах ряда
qдив = 2.48 GJ/ cyαb2e l2 ,
т.е. по сравнению с точным решением
qдив(2 чл)/ qдив(точн) = 1.06 ;
Vдив(2 чл)/ Vдив(точн) = 1.03 ;
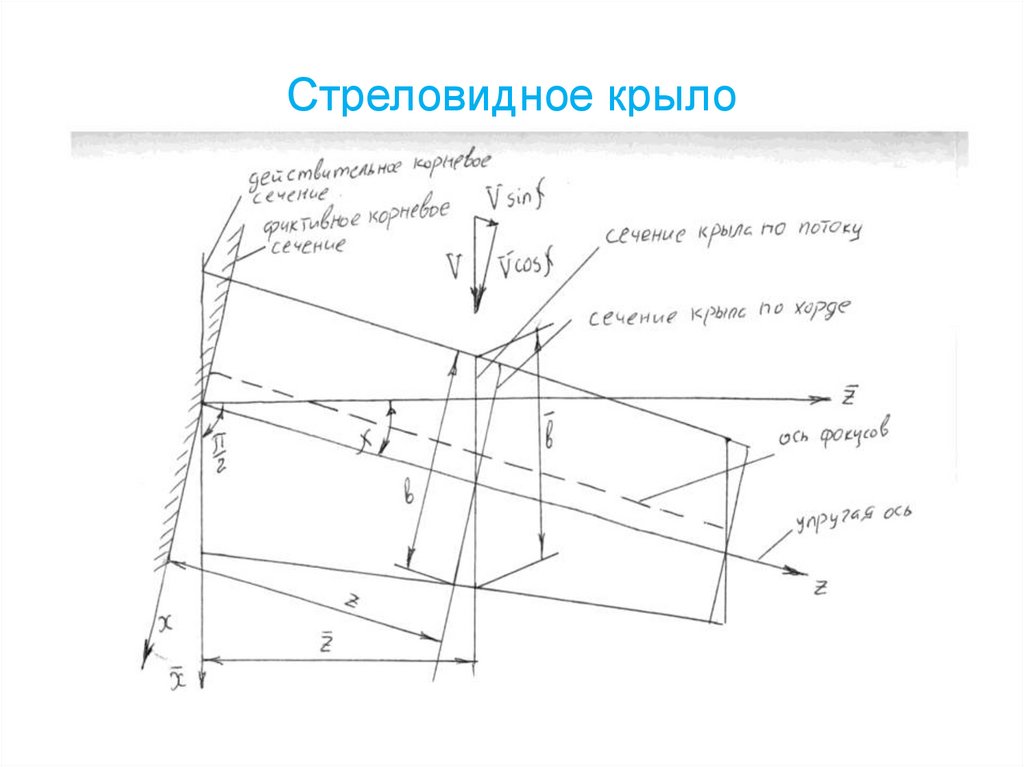
189. Стреловидное крыло
190.
Стреловидное крыло191. Сведения из теории оболочек
192. Безмоментная оболочка
Геометрическиесоотношения
1 u w
;
R1 R1
1 v u
w
cos ;
r r
R2
Уравнения равновесия
N
r
(rN ) R1
N
rR1 0;
x
N
r
R1
(rN ) N
rR1 0;
N N
Z 0 уравнениеЛапласа
R1 R2
r v 1 u
;
R1 r r
Физические соотношения
1
N N ;
E
1
N N ;
E
E
N
G
;
2(1
)
G
193. Моментная оболочка
194. Круговая моментная цилиндрическая оболочка при осесимметричной деформации
(Nxy=Qy=Mxy=0; v=0;)Уравнения равновесия
dN x
X 0
dx
dQx N y
Z 0
dx
R
dM x
Qx 0
dx
Гипотеза Кирхгофа - Лява
(1)
u z ( x) u ( x)
dw( x)
z
dx
(2)
где u ( x) и w( x ) - продольные
и нормальные перемещения точки,
лежащей на срединной поверхности
dw( x)
- угол поворота нормали.
dx
195. Моментная оболочка (продолжение)
/2Nx
/2
x dz; N y
/2
E du
w
Nx
;
2
(1 ) dx
R
d 2w
d 2w
M x D 2 ; M y D 2 ;
dx
dx
где
E 3
D
;
2
12(1 )
/2
y zdz;
(3)
E w
du
Ny
;
2
(1 ) R
dx
(4)
y dz; M x
/2
/2
/2
x zdz;
My
/2
dM x
d 3w
Qx
D 3 ;
dx
dx
(5)
196. Моментная оболочка (продолжение)
Nd 4 w E
D 4 2 w Z x ; (7)
dx
R
R
(6)
окончательно
Ny
1
Z
D
(8)
E
3(1 2 )
k
4R2 D
R 2 2
(9)
w IV 4k14 w
E
w Nx;
R
где
4
1
Решение уравнения (8)
w ek1x (C1 cos k1 x C2 sin k1 x) e k1x (C3 cos k1 x C4 sin k1 x ) w
В зоне краевого эффекта:
w e k1x (C3 cos k1 x C4 sin k1 x) w
197. Расчет осесимметричных оболочек
Уравнения равновесияГде Р – равнодействующая
всей внешней нарузки
Физические соотношения
u
w
R1 R1
u
w
ctg
R2
R2
198. Примеры
Сфера:P p0 r 2 p0 ( R 2 sin 2 )
p0 R
N
2
R1 R2 R
p0 R
N
2
Цилиндр:
R1
p0 R
N
2
R2 R
90
N p0 R
Конус:
R1
R2 x tg
P p0 ( R 2 sin 2 )
N p0 x tg
p0 x tg
N
2




























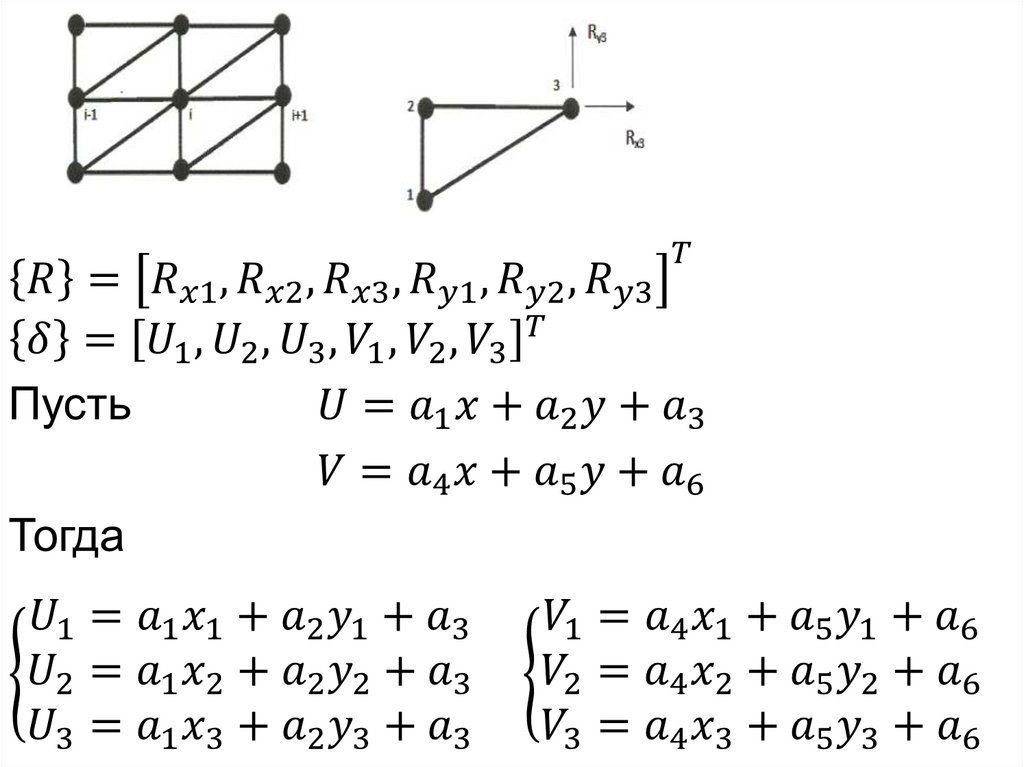











































 physics
physics








