Similar presentations:
Антенные системы средств связи
1. Антенные системы средств связи
2. Лекция 1 Антенна
Преобразователь модулированных ВЧ-колебаний(возбуждаемые передатчиком), излучающий их в
форме электромагнитных волн в окружающее
пространство (промежуточную среду).
Элмаг.волны достигают приемную антенну, где
под их действием индуцируются токи ВЧ,
поступающие на вход приемника.
3.
Назначение антенн при передаче, приеме, общаяхарактеристика.
Г
Фидер
тракт
Фидер
Фидер тракт
тракт
Прм
Упр.
устр-во
Устр-во
Упр.устр-во
обр
рис.1Блок схема прохождения радиосигнала от передатчика до приемника
модулятор
Передающая антенна- устройство, предназначенное для
преобразования направляемых электромагнитных волн,
движущихся
по
фидеру
ко
входу
антенны,
в
электромагнитные волны свободного пространства и
излучение их в пространство.
Приемная антенна- устройство, служащее для приема
свободных электромагнитных волн и преобразование их в
направляемые волны фидера, подводящие принятую
мощность ко входу приемника.
4. Требования к параметрам антенн для эффективного функционирования радиосистемы
1-определенная характеристиканаправленности (равномерное принятие и
излучение энергии по всем направлениям),
2-высокий КПД.
3-поляризационная характеристика,
4-выбор рабочей частоты,
5-размеры (габариты) антенны,
6-конструкторские требования.
5. Фидерный тракт
Осуществляет «канализацию»электромагнитной энергии.
Обеспечивает
соответствующий режим
входной, выходной цепей
передатчика и приемника.
Выполняет предварительную
частотную фильтрацию
сигналов.
Управление положением луча в
пространстве.
6. Физические основы излучения Это взаимодействие зарядов с электромагнитным полем
В передающей антеннеТоки(поля)в раскрыве возбуждают электромагнитное
поле в пространстве, поле «уходит» необходимо
поддерживать передачу энергии от движущихся в
антенне зарядов полю.
В приемной антенне
Поле воздействует на свободные заряды антенны, что
приводит к возникновению переменного тока
Принцип
обратимости
антенн
7.
ФАРАнт. с обр. сигнала
8. Параметры антенн
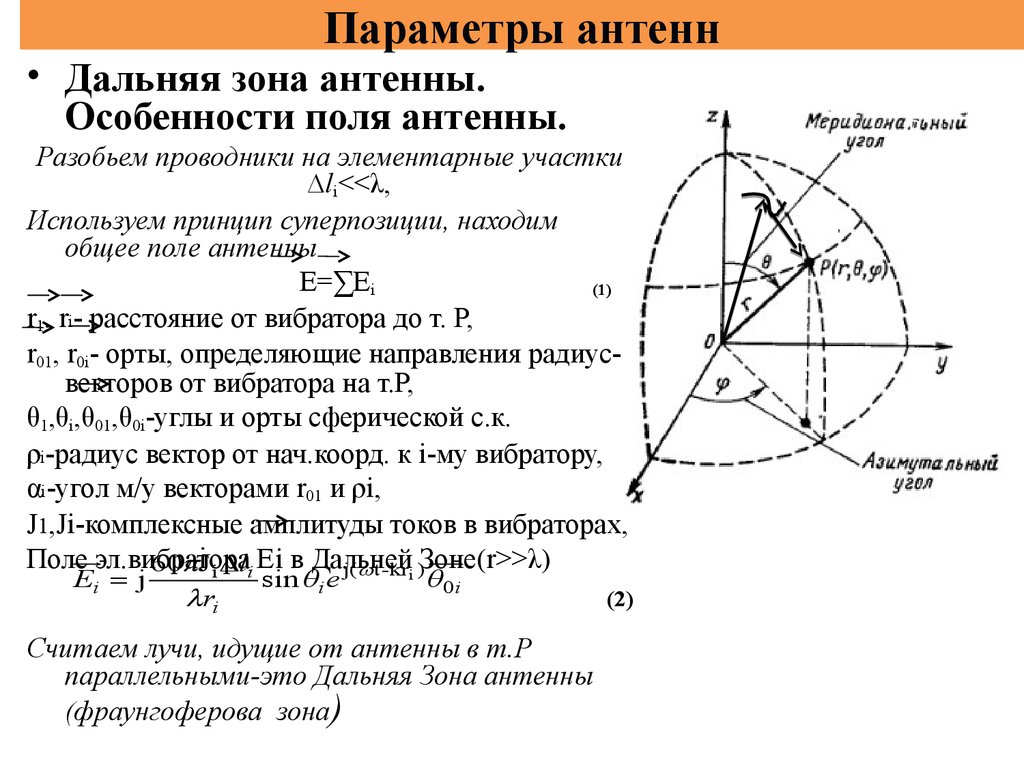
• Дальняя зона антенны.Особенности поля антенны.
Разобьем проводники на элементарные участки
∆li<<λ,
Используем принцип суперпозиции, находим
общее поле антенны
E=∑Ei
(1)
r1, ri- расстояние от вибратора до т. Р,
r01, r0i- орты, определяющие направления радиусвекторов от вибратора на т.Р,
θ1,θi,θ01,θ0i-углы и орты сферической с.к.
ρi-радиус вектор от нач.коорд. к i-му вибратору,
αi-угол м/у векторами r01 и ρi,
J1,Ji-комплексные амплитуды токов в вибраторах,
Поле эл.вибратора
60 J i li Еi в Дальней
j( t - kri )Зоне(r>>λ)
Ei j
ri
sin i e
0i
Считаем лучи, идущие от антенны в т.Р
параллельными-это Дальняя Зона антенны
(фраунгоферова зона)
(2)
V
S
Р’
li
ri
9.
Определим границу Дальней Зоны:L-макс. линейный размер антенны,
из параллельности лучей в т.Р r=r1-Lcosα,
∆r11=r-r1= -Lcosα разность хода лучей
L
r r L 2r L cos r 1
Из ∆ОВР имеем:
Используем разложение
бинома Ньютона:
2
2
1
2
2
1
1
2r1 L cos
r 21
L
sin 2
2r1
L2
r r1 L cos
sin 2
2r 1
r r1 L cos
rист
L2 2
rист r11 sin
2r1
Лучи считаем параллельными если
Критерий Дальней Зоны r1>>L2/λ
полагают r1>>2 L2/λ
ri r1 i cos i r1 i r01 (9),
Подставляя (9) в (2), (1), полагая ∆li=∆l, находим
60 J i li j ( t kr1 )
Ji
jk i r0 i )
Ei j
e
sin
e
i 0i J
i
ri
1
зависит от распределения токов в антенне и ее геометрии
(3)
(4)
(5)
(6)
(7)
(8)
(10)
10. Таким образом поле любой антенны в Дальней Зоне представляется в виде
e j ( t kr1 )E i J1 f ( , )
r1
(11)
где векторная комплексная функция
60 l
Ji
jkr0 i
f ( , ) j
0i sin i e
J1
i
f ( , ) f ( , )e jФ ( , )
(12)
(13)
11. Особенности поля любой антенны в ДЗ
Вектора поля Е и Н связаны между собой как в плоской волне.
1
r01 Ei
H
z0 E
Hi
,
zc
zc
• Поле антенн имеет поперечный характер, т.к. 0лежат
в одной
i
плоскости перпендикулярной r0 от антенны к т. Р
• Зависимость поля от расстояния имеет вид сферической волны,
сходно с точечным источником в начале координат
e
j ( t kr1 )
r1
• Характер изменения поля в пространстве определяется
векторной функцией f ( , ) -векторная комплексная диаграмма
направленности (DH), зависящая от распределения токов в
антенне и геометрии расположения.
12.
Модуль функции характеризует зависимость амплитуды поляантенны от пространственных углов, называется амплитудной
DH антенны по полю f(θ,φ)
Аргумент функции характеризует зависимость начальной
фазы поля от пространственных углов, называется фазовой
DH антенны Ф(θ,φ)
13. Лекция 2 Диаграмма направленности по полю и по мощности
DH по полю f(θ,φ) - зависимость амплитуды поля, излучаемогоантенной, от пространственных углов θ,φ при постоянном расстоянии
до точки наблюдения и неизменных условиях возбуждения антенн.
f ( , )
F ( , )
f MAX ( , )
(1)
DH по мощности- зависимость плотности потока излучаемой мощности
П от пространственных углов θ,φ при постоянном расстоянии до точки
наблюдения и неизменных условиях возбуждения
P ( , ) F ( , )
игольчатая
веерообразная
2
(2)
косекансная
14. DH характеризуется :
Ширина DH 2θ0,5р, определяется как уголмежду направлениями, в которых плотность
потока мощности уменьшается в 2 раза, 10 раз,
до 0 по сравнению с направлением главного
максима,
УБЛ (уровень боковых лепестков) определяется
как отношение max боковых лепестков к
главному max (в %, Дб).
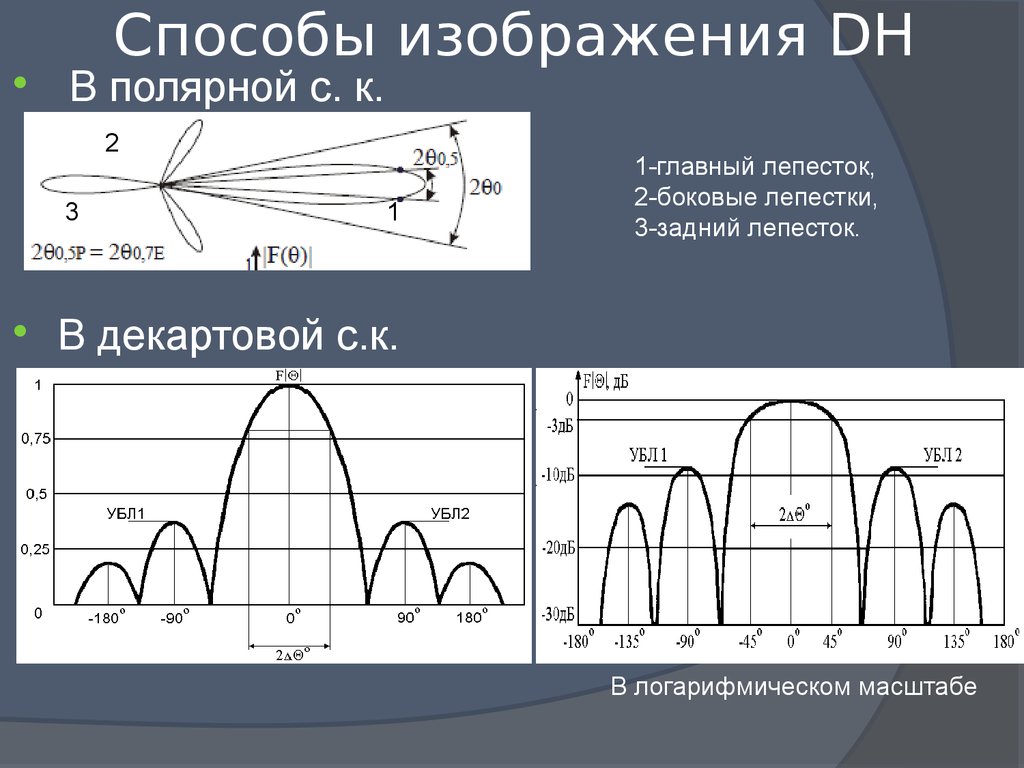
15. Способы изображения DH
В полярной с. к.2
3
1
1-главный лепесток,
2-боковые лепестки,
3-задний лепесток.
В декартовой с.к.
В логарифмическом масштабе
16.
17. Фазовая DH
Ф(θ,φ)=argf(θ,φ)-зависимость начальной фазы поляот пространственных углов θ,φ при фиксированном
расстоянии от начала координат и неизменных
условиях возбуждения антенны. Зависит от
положения начала координат на антенне.
Фазовый центр антенны-положение начала
координат, относительно которого Ф(θ,φ)=const или
меняется на при переходе от одного лепестка к
другому.
• Эквифазная поверхность (фронт волны) поверхность
в пространстве, во всех точках которой в данный
момент фаза поля одинакова.
18. КНД=D(θ,φ)- коэффициент направленного действия
D(θ,φ)=PE0/PE при E(θ,φ)=E0 т.е. показывает восколько раз мощность PE0, излучаемая изотропной
антенной должна быть больше мощности PE,
излучаемой рассматриваемой антенной, при
условии равенства возбуждаемых ими в
направлении θ,φ полей.
D(θ,φ)=E2(θ,φ)/E20 при PE0=PE т.е. показывает во
сколько раз плотность потока мощности,
излучаемой направленной антенной в направлении
θ,φ больше плотности потока мощности ,
излучаемой изотропной антенной в окружающее
пространство.
19.
КНД определяют в направлении максимума излученияF2(θ,φ)=1.
В произвольном направлении:
D( , ) Dт F 2 ( , )
4
Dт
(3)
2
0
2
F
( , ) sin d d
(4),
0
КНД в данном направлении
характеризует
выигрыш в мощности излучения за счет
направленных свойств антенны.
Чем уже DH, тем выше КПД
20.
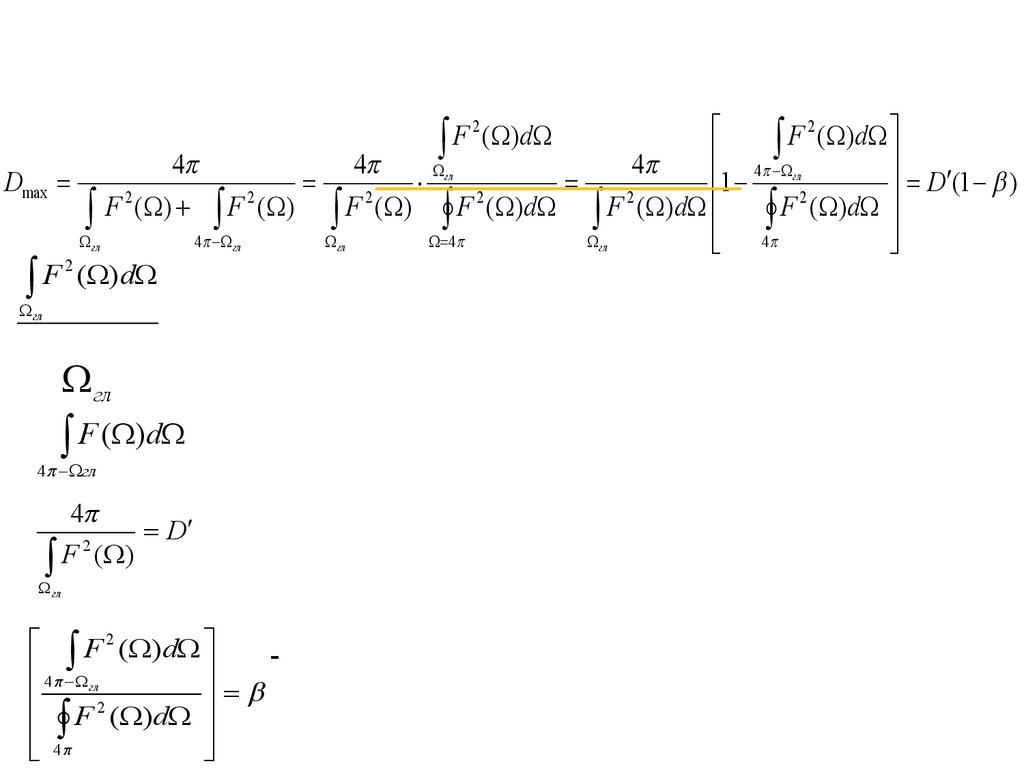
Зависимость КНД от ширины лучаи уровня боковых лепестков
2
F
( ) d
4 гл
4
4
4
гл
Dmax
1
D (1 )
2
2
2
2
2
2
F ( ) 4 F ( ) F ( ) 4 F ( )d F ( )d 4 F ( )d (5)
гл
гл
гл
гл
2
F ( )d
гл
-мощность излучения приходящая на главный лепесток DH,
2
F
( ) d
гл
-телесный угол, занимаемый главным лепестком DH,
F ( ) d
-мощность излучения, приходящаяся на область боковых
и задних лепестков DH,
4
D
2
F ( )
-КНД по главному лепестку DH,
4 гл
гл
2
F
( ) d
- полный коэффициент рассеивания, относительная доля
4 гл
мощности излучения антенны, приходящуюся на область
2
F ( ) d
боковых и заднего лепестков DH.
4
21. КУ=G(θ,φ)-коэффициент усиления
22. Входное сопротивление антенны
Zвх - отношение комплексной амплитуды напряжения Uвхк комплексной амплитуде тока J вх антенны
Z U A R ( f ) jX ( f )
ВХ
вх
вх
IA
Z
Z
0
Г ВХ
Z ВХ Z 0
(9),
-коэффициент отражения на
входе антенны, позволяет
определить Zвх, т.к. для вычисления Rвх , Хвх
следует найти точные значения J и U
Z ВХ
Г 1
Z0
1 Г -нормированное сопротивление антенны
23.
Сопротивление излученияRE -коэффициент с помощью которого, зная ток в антенне,
определяют излучаемую мощность
PE =J2 RE /2
(10),
P
Sсс
J2 1
П ( , )dS
2 120
2
f 2 ( , ) sin( )d d
0 0
(11),
D( , )
4 f 2 ( , )
2
(12),
f 2 ( , ) sin d d
0 0
Сравнивая (11)и (12) получаем
D(θ,φ)=f2(θ,φ)/30RE
(13) .
24. Поляризационная DH антенны
Зависимость коэффициента эллиптичности от пространственныхуглов θ,φ
.
e jkr
E E 0 E J f ( , ) 0 f ( , ) 0
r
0
Конец вектора E описывает за период ВЧ эллипс.
Характеризуемый параметрами:
коэффициентом эллиптичности р=в/а <1,
углом наклона большой полуоси эллипса β,
направлением вращения вектора E
(14)
25. Рабочий диапазон частот антенны
Интервал частот, в котором заданные параметры антенныне выходят из заданных границ.
∆f= fmax-fmin=f1(Zвх), Zвх=f2(КСВ), то ∆f=f3(КСВ)
Определяющие полосу рабочих частот параметры
антенны: КНД, 2θ0,5р, УБЛ, коэффициент эллиптичности,
При задании границ изменения нескольких параметров
∆f/f относительная полоса работы
Антенна
∆f определяется тем, который изменяется
быстрее
<10%
узкополосная
<10…50%
широкополосная
Кд=fmax/fmin (коэф. перекрытия диапазона)
Антенна
≥2
диапазонная
≥5
частотно-независимая
26. Теория приемных антенн
Лекция 327. ПРМ антенна преобразует энергию радиоволн ВЧ эл.магнитного поля в энергию токов ВЧ Решение вопросов: 1. Какова величина ЭДС и тока приемной
ПРМ антенна преобразует энергию радиоволнВЧ эл.магнитного поля в энергию токов ВЧ
Решение вопросов:
1. Какова величина ЭДС и тока приемной антенны
при заданной напряженности поля падающих
радиоволн,
2. Как зависят эти величины от DH антенны,
3.Чему равно входное сопротивление приемной
антенны;
4. Чему равна мощность, отдаваемая антенной
приемнику.
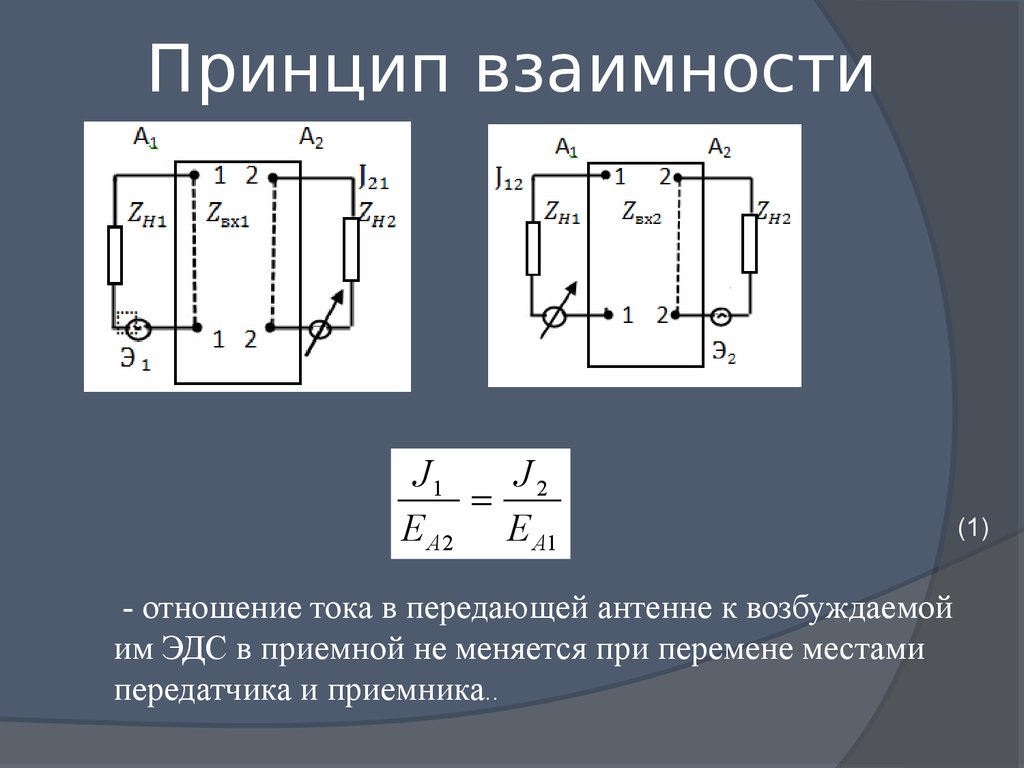
28. Принцип взаимности
J1J2
E A2 E A1
- отношение тока в передающей антенне к возбуждаемой
им ЭДС в приемной не меняется при перемене местами
передатчика и приемника..
(1)
29. Ток в приемной антенне
Известно F(θ,φ),Dmax, R∑,Zвх, r в режиме передачи:
E21
учитывая, что
60 Dmax 1P
F1 ( , )
r
P∑ =J2 R /2
Э
I 1
Zн1 Zвx1
∑
Э1
(2),
(3),
(4),
rЕ21 Zн1 Zвх1
30 P 1 D max1 F1 ( 1, 1)
(5),
Э2
rЕ12 Zн 2 Zвх 2
30 P 2 D max 2 F 2( 2, 2)
(6)
30.
В соответствии с принципом взаимности имеем:Э 2 J 12
Э1 J 21
(7),
Величина Е12 зависит от параметров 2 антенны, но отношение
Е12 к вызванному ею же току в 1 антенне J12 зависит от параметров
1 антенны.
Для произвольной антенны
F ( , ) Dmax1 P E
const N
Zн Zвх
J
(8),
F ( , ) Dmax1 P 1
Э
J
Zн Zвx
N Zн Zвx
(9).
Приемная антенна рассматривается как генератор с ЭДС
31.
Определим N:El
Э El sin
120 sin
N
- ЭДС на вибраторе длиной l
N
120
Выражения принимают вид:
(10),
Отсюда
E
J
Z H Z B
E
Э
R Dmax
F ( , )
120
R Dmax
F ( , )
120
(11),
(12),
(13).
Если DH приемной антенны назвать зависимость амплитуды ЭДС в
приемной антенне от углов θ, φ, характеризующих направление
прихода плоской электромагнитной волны при постоянной величине
напряженности поля в месте приема, то она совпадает с DH этой
антенны в режиме передачи
32.
Определим мощность в нагрузке:Pн
учитывая, что
Э2
Rн
2
Zн Zв 2
(14)
D( , ) Dт F 2 ( , )
G(θ,φ)=D(θ,φ)η
Находим:
E 2 2
Pн
G ( , )
240 4
где G(θ,φ)- параметр передачи
(15)
33.
2Sэ( , )
G ( , )
4
(16),
- эффективная площадь антенны, параметр приема
Sэ max
(17),
Sгеом
- коэффициент использования поверхности раскрыва
КНД приемной антенны в направлении θ,φ - отношение мощности,
поступающей на вход приемника при приеме с направления θ,φ к
среднему, при приеме по всем направлениям значению мощности,
поступающей на вход приемника.
КНД приемной антенны=КНД передающей антенны
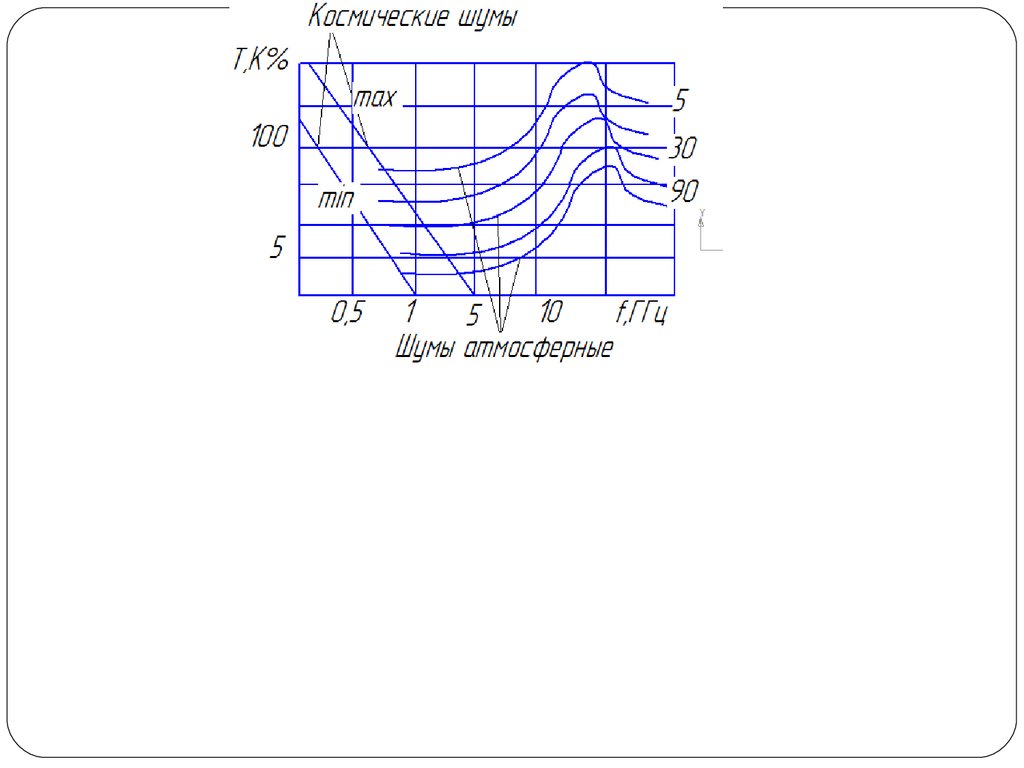
34. Основной источник внешних шумов в диапазоне УКВ:
1. тепловое радиоизлучение земной поверхности;2. космическое радиоизлучение, включая радиоизлучение планет
и звезд;
3. тепловое радиоизлучение земли и предметов, расположенных
вблизи антенн.
На ТА влияют земля, окружающие антенну предметы с шумовой
темп. 2900 К
35.
Рис.1 Зависимость шумовой температуры космических шумови шумов атмосферы от частоты и угла места
β= βn+βз –коэф. рассеивания, для оценки величины шумовой
температуры, характеризуют какая часть мощности
поступает в антенну через боковые лепестки переднего и
заднего полупространства.
ТА=Тг(1- β)+Тnβn+ βзТз- шумовая температура
(23),
идеальной антенны
ТА=Тг(1- β)+Тnβnη+ βзТз η +Т0(1- η)
(24).
36. Особенности антенн
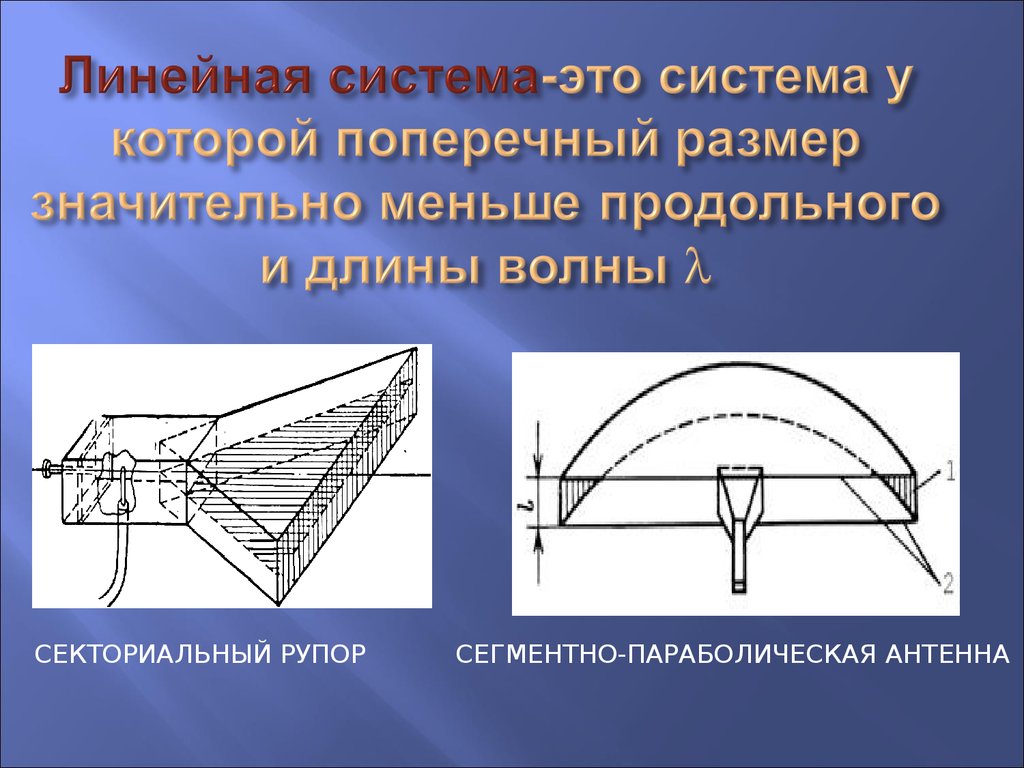
37. Линейные системы непрерывно распределенных излучателей
Лекция №538. Линейная система-это система у которой поперечный размер значительно меньше продольного и длины волны
СЕКТОРИАЛЬНЫЙ РУПОРСЕГМЕНТНО-ПАРАБОЛИЧЕСКАЯ АНТЕННА
39.
Излучатели распределены непрерывно вдоль оси zL/2
fсист
I z e
j ( z ) kz sin
dz
L / 2
(1)
Переходя к новым переменным:
z
x
,
L/2
Имеем:
L
sin
2 L
kz sin
x sin x
2
(2)
1
L
j x
fсист( ) I ( x)e dx
2 1
,где
I(x)=I(x)ej (x)
40.
Замечание:1.Множитель системы представляет собой угловой
спектр АФР
2.Необходимое и достаточное условие
существования фазового центра в линейных
антеннах :
Если (x)=I(-x)-четная.функция, (-x)=- (x) фазовое
распределение нечетная. функция, то fсист(x)
вещественная функция.
41.
Влияние амплитудного распределенияна множитель системы DH
1
L
fсист( ) I ( x)e x dx
2 1
(3)
L sin
Fсист( )
(4)
Система с равномерным амплитудным распределением.
Fсист( )=sin / (4 “) -нормированный множитель системы
1. Нули DH =±π, ±2π,…
2. max боковых лепестков =±(2k+1) π/2, k=1.2…
б1=4,71 б2=7,82
Значение уровня боковых лепестков:
sin б
1
Fб
б
(2k 1)
2
Fб1 0.212(21.2%)
Fб 2 0,127(12,7%)
Fб 3 0,091(9,1%)
(5)
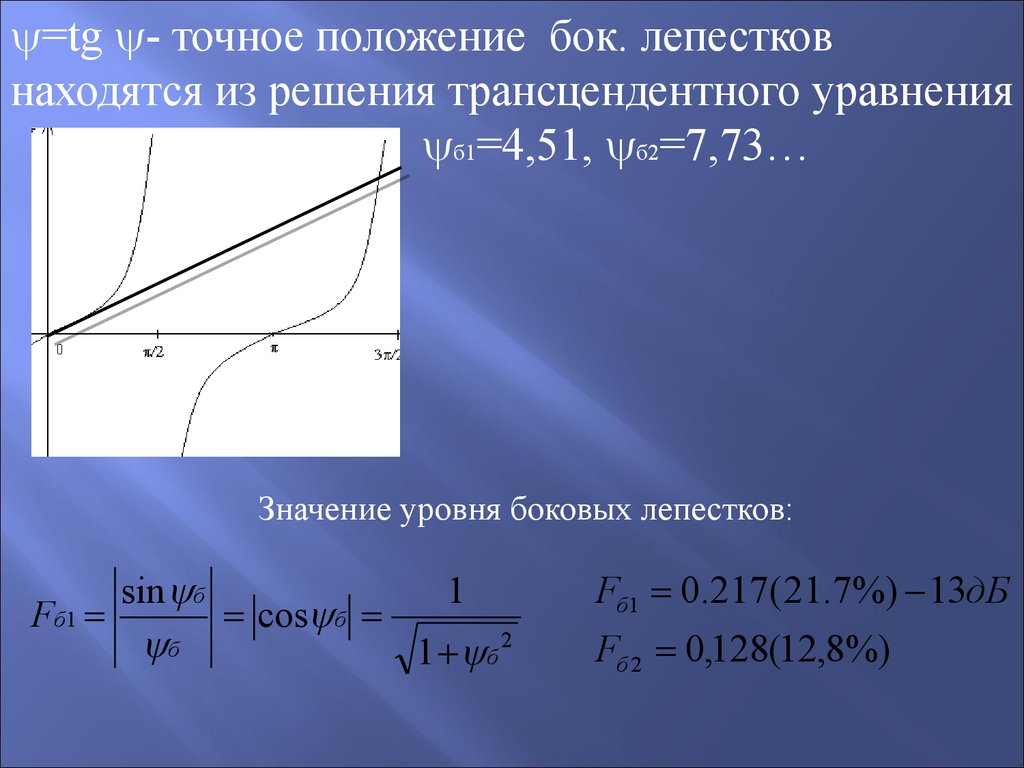
42.
=tg - точное положение бок. лепестковнаходятся из решения трансцендентного уравнения
б1=4,51, б2=7,73…
Значение уровня боковых лепестков:
sin б
1
Fб1
cos б
б
1 б 2
Fб1 0.217(21.7%) 13дБ
Fб 2 0,128(12,8%)
43.
3. Ширина DH2 0,5р=2,78 /π или 2 0,5р=51 /L
-π/2≤ ≤ π/2
0.5p=1.39 -a≤ ≤a – рабочая область,
где а = πL/
4.КНД
a
1
2
2af
2f
L
2
2
D
f
d
2
A
x dx
сист
,
4
f
cos
f
d
a
1
сист
/2
2
2
сист
а
2
2
сист
сист
/ 2
а
2
A x dx
1 1
2L
D
1
2
2
A x dx
1
1
КИD - АНАЛОГ КИП апертурных антенн,
при А(х)=1 , D=2L/
44. Система с косинусоидальным распределением А(х)=cosπx/2
1L
x j x
fсист( ) cos e dx
2 1
2
sin
sin
1
fсист( )
L
2
2
2
2
2
0
А(x)
-1
sin
sin
2
2
cos
Fсист( )
2
4
2
2
2 1
(12)
(13)
Ширина DH 2 0,5р=1,84; 2 0,5р=67 L ;
=±(2k+1)π/2, k=1,2…
Fб1=7% или -23 дБ
L
D 1.62 (14)
Ширина DH ↑, УБЛ↓, КНД↓
45. Система «косинус на пьедестале» А(х)=+(1- )cosπx/2, где 0≤≤1
(15)Система «косинус на пьедестале»
А(х)= +(1- )cosπx/2,
sin( ) sin
sin 1
2
2
fсист( ) L{
[
]}
2
2
2
где
0≤ ≤1
fсист( ) L 2 / 1
(16)
(17)
sin
sin( )
1
sin 1
2
2
Fсист( )
{
[
]}
2 / 1
2
2
2
(18)
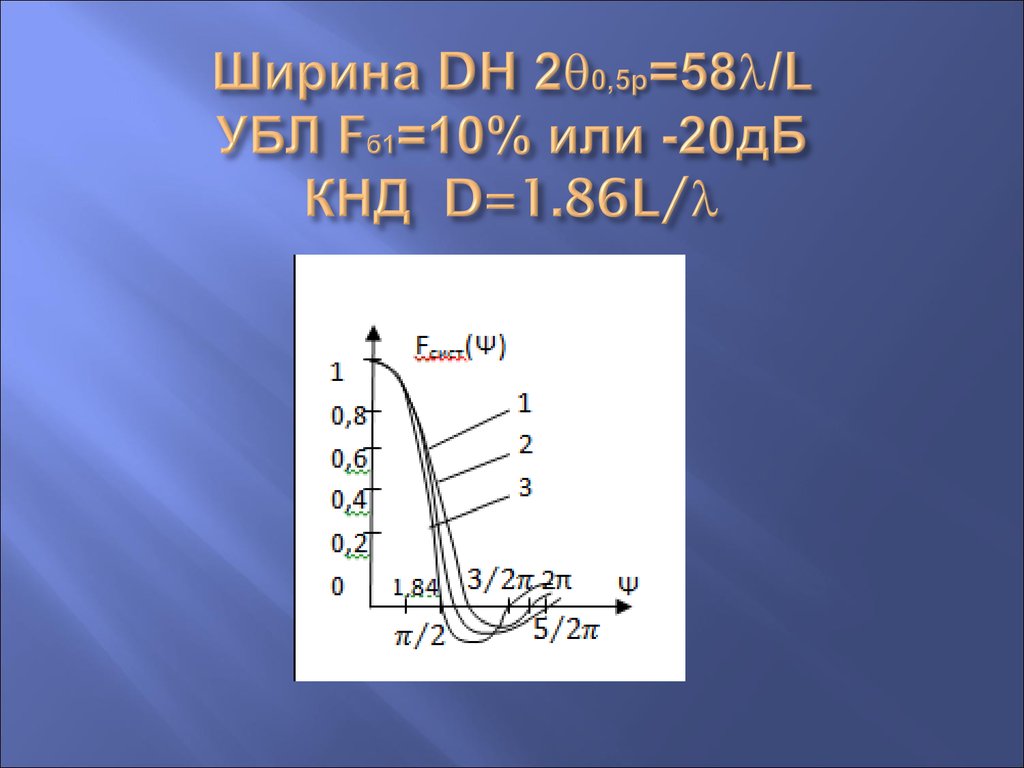
46. Ширина DH 20,5р=58/L УБЛ Fб1=10% или -20дБ КНД D=1.86L/
47. Система с линейным фазовым распределением
1L j ( ( x ) x )
dx
Пусть А(х)=1, fсист( ) e
2 1
L j x
sin( a )
fсист( ) e dx L
2 1
a
1
(19)
φ(x)=-ax
нормированная DH
sin( a)
Fсист( )
a
sin m=a /πL
(21)
(20)
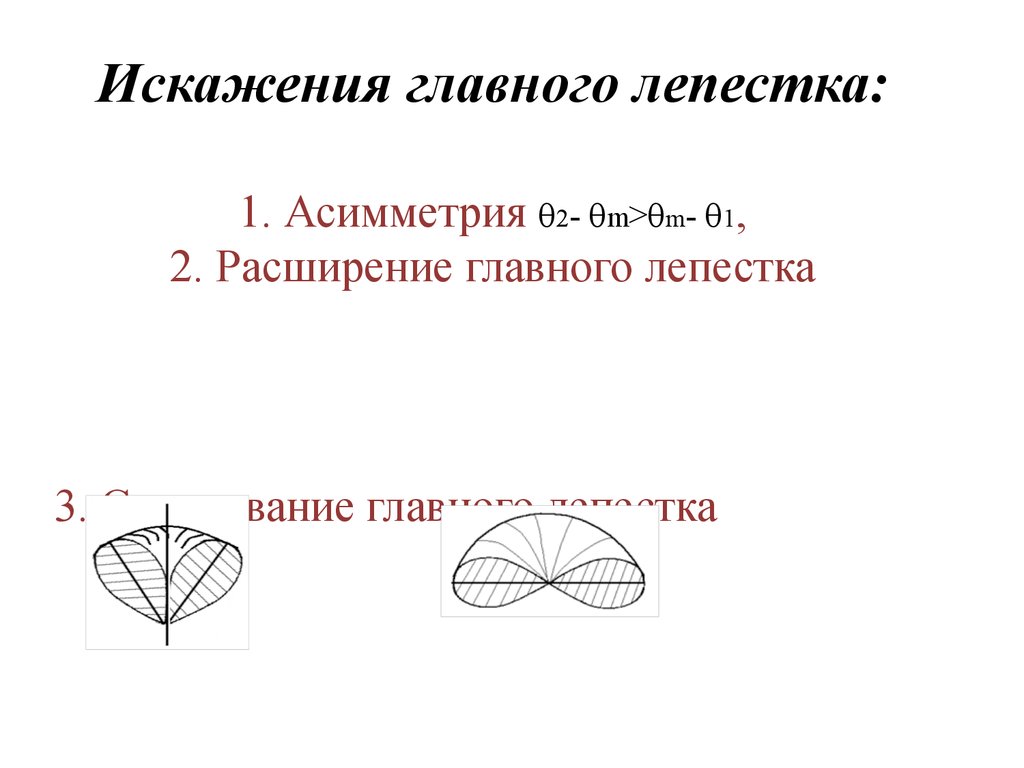
48. Искажения главного лепестка: 1. Асимметрия 2- m>m- 1, 2. Расширение главного лепестка
Искажения главного лепестка:1. Асимметрия 2- m> m- 1,
2. Расширение главного лепестка
ψ2-ψ1=2,78
2θ0,5роткл=2θ0,5р*1/cosθm
c↑ θm главный лепесток DH
расширяется.
3. Свертывание главного лепестка
Воронкообразное F(θ)=sinθ
49. Система с квадратичным фазовым распределением.
φ(x)=-ax2 , a>01
L j ( ax 2 x )
fсист( ) e
dx
2 1
(26)
Условие существования фазового центра нет, т.к. функция четная.
Диаграмма искажается симметрично.
│φmax │≤π/8 искажений DH нет, пропадание нулей,
↑│φmax│нули DH «заполняются» сильнее, боковые лепестки
растут и сливаются с главным.
│φmax│=π главный лепесток имеет провал и вдвое большую
ширину
50.
51. Система с кубическим фазовым распределением.
φ(x)=-ax31
L j ( ax3 x )
fсист( ) e
dx
2 1
Система имеет фазовый центр, DH искажается не симметрично.
52. Методы анализа излучения непрерывных антенн
Лекция 453.
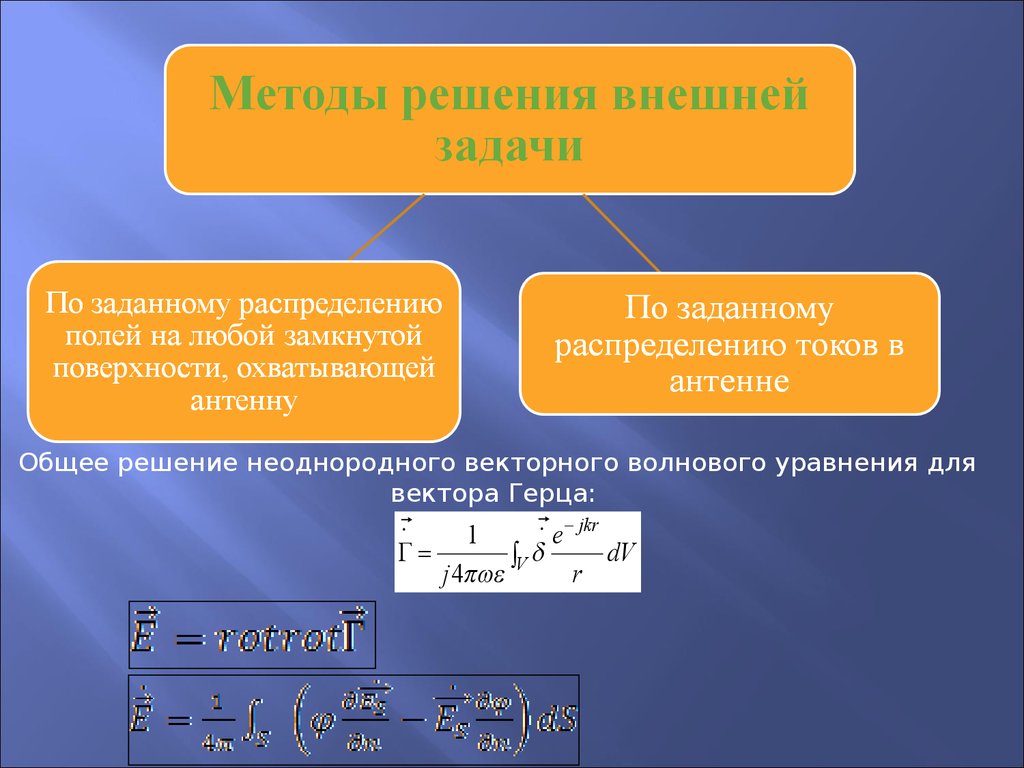
54.
Общее решение неоднородного векторного волнового уравнения длявектора Герца:
e jkr
1
dV
V
j 4
r
55.
Вторичные источники представляют собой элементарныеплощадки поверхности S с соответствующими значениями поля,
возбуждаемые токами, находящимися внутри области, охваченной
поверхностью S.
Э
S nH S ,
M
S nES .
(1)
Электромагнитное поле линейно поляризовано, составляющие
элемент поверхности
рассматривается как совокупность двух взаимно
ортогональных электрического и магнитного диполей с моментами.
SM S E S S .
(2)
E
SЭ S H S S S S ,
Z0
56.
1e jkr
E j
E S S (1 cos ) cos
,
2
r
1
e jkr
E j
E S S (1 cos ) sin
.
2
r
(3)
элементом Гюйгенса создает сферическую волну. Поле излучения его имеет
линейную поляризацию
Амплитуда поля:
(4)
Z
E ~ 1 0 cos ,
Z
Z
E ~ 1 0 cos .
Z
(5)
При расчете полей излучения реальных апертурных антенн достаточно
учитывать
поле в раскрыве
т.к. результирующие поле согласно принципу
,
суперпозиции определиться суммой полей элементарных источников Гюйгенса.
57. Поле системы идентичных, одинаково ориентированных излучателей. Правило перемножения диаграмм.
Поле любой антенны в силу принципа суперпозиции:E Ei ,
i
Пусть антенна- дискретная система из N идентичных, одинаково
ориентированных излучателей, произвольно размещенных в
пространстве, тогда поле антенны в т.Р:
В дальней зоне θі=θ
и φі=φ,
E J i f , e jkri
i
i i i
ri
f i ( , ) f i ( , )
J 1 e jkri
Ei f 0 ( , ) J 0
ri
i J 0
ri=r-ρr0=r-ρicosαi
(14)
(15)
(16)
58.
Ei f 0 ( , ) J 0 eJ i I i e jФi
Ii
Ai
I0
i Фi Ф0
Ii
jФ1
Ai e
I0
jkr
r
J 1 e jkr cos i
i J 0
где I,Ф – амплитуда и фаза в излучателе
«i».
-амплитудное распределение тока в системе
антенной решетки.
-фазовое распределение.
-амплитудно-фазовое распределение
59.
jkr N 1e
j
k
cos
d
i
E J 0 f 0 ,
E0 f сист , ,
Ai e i i
r i 0
множитель системы, величина не зависит от типа излучатели, из которых
состоит антенна, определяется АФР токов в системе и пространственным
расположением излучателей. Описывает пространственную
интерференционную DH системы изотропных излучателей.
амплитудная DH системы изотропных излучателей
фазовая DH этой системы
Ei f 0 ( , ) J 0e
jk 2
2
Результирующая векторная диаграмма
f ( , ) f 0 ( , ) f сист ( , )
правило перемножения диаграмм, правило Бонч-Бруевича (1924 г.)
Ei f 0 ( , ) J 0e
jkr N 1
r
A
i 0
e j (Фi kФ2 cos )
i
Полное поле системы одинаково ориентированных диполей в дальней зоне.
60. Следствия:
• если излучатель имеет в какой-то плоскостиненаправленную DH, то результирующая, DH
совпадает с множителем системы,
• поляризация поля сложной антенны
определяется типом излучателя, а DH в
основном множителем системы,
• влияние DH излучателя на результат DH
наиболее существенно в направлениях θ, φ,
где DH излучение имеет нули.
61. Плоские двумерные системы непрерывно распределенных излучателей
Лекция 662. Прямоугольный раскрыв
Раскрыв антенны представляет двумерную систему идентичныходинаково ориентированных излучателей Гюйгенса , если фронт
волны в раскрыве антенны мало отличается от плоского и
поляризация поля во всех точках раскрыва одинакова
x
(1)
P
P1
Прямоугольный раскрыв
0
z
θ
y
(2)
Рис. 1
Учитывая ρcosα=ρr0, находим ρcosα = xsinθcosφ + ysinθcosφ
(3)
x
P
P1
(4)
θ
z
L1
y
L2
r0
63.
Распределение с разделяющимися переменными(5)
(6)
y
(7)
Для плоскости ХОZ φ=0
(8)
Для плоскости YOZ φ=π/2
(9)
При разделяющемся АФР в прямоугольном раскрыве множители
системы в главных плоскостях совпадают с множителями линейных
систем, как и АФР в раскрыве вдоль осей x и y. Задача сводится о
двух линейных системах, ориентированных параллельно сторонам
прямоугольника.
64.
При постоянном АФР в раскрыве(10)
Где
плоскостей XOZ и YO0Z.
Нормированные DH в плоскости XOZ:
(11)
(12)
65. Круглый раскрыв
,,
(13)
,
(14)
Часто используют синфазные раскрывы с амплитудным
распределением, не зависящая от φ,. Полагая
,
(15)
Используя интегральное представление для функции Бесселя
нулевого порядка
Получаем
,
,
Раскрыв излучает сферическую волну.
Фазовый центр в центре раскрыва.
(16)
66.
Если А(р)=1- равномерное АР, то,
,
,
Учитывая соотношение
Получим
f
(17)
Переход от прямоугольному к круглому раскрыву приводит к
расширению главного лепестка DH и снижению УБЛ.
УБЛ круглого раскрыва Fб1=13% или 17дБ
ШDH
, где
При ρ0>>λ
(18)
Для АР вида
(19)
,
где
,
67.
Интегрируя, получаем:(20)
запишем через табулированную лямбда-функцию
(21)
(22)
(23)
Таблица со значениями Р для АР в раксрыве, апроксимирующиеся
функцией вида (20).
Фазовые искажения в круглом раскрыве приводят к таким
же изменениям DH, что и для линейных систем.
68. КНД синфазного излучающего раскрыва.
Амплитуда поля в направлении главного max:(24)
где Е0(0)- амплитуда поля центрального излучателя Гюйгенса един.
площади в направлении θ=0
(25)
(26)
(27)
Учитывая (24)-(27), получаем
(28)
(29)
КИП антенны в режиме приема
69.
Если А(х,у)=1 – равномерное АР, тогда КНД будет максимальным.(30)
Синфазное отверстие с равномерным АР называют идеальной
антенной.
γ=Sэфф/Sгеом – КИП излучающего раскрыва
(31)
КИП синфазного раскрыва показывает на сколько снижается КНД
антенны из-за неравномерности АР.
70. антенны
АНТЕННЫЛекция 13
71. Принцип действия зеркальной антенны
Основные типы зеркал:1.параболические(параболоид вращения и
параболический цилиндр);
2.сферические;
3.плоские и уголковые;
4. спец. формы.
По числу используемых зеркал
однозеркальные и многозеркальные
DH формируются вследствии различного АФР,
зависящий от формы зеркала.
72. Классификация зеркальных антенн
1. Параболические ЗА- создают остронаправленноеизлучение(узкую DH)
2. Сферические ЗА- качают луч в широких пределах без
искажения его формы, перемещая облучатель по дуге окружности.
3.Плоское зеркало- рефлектор в вибраторных, уголковых и
перископических антеннах для изменения направления
распространения электромагн. волн.
4. Зеркало спец. формы- формирует DH спец. формы
Для уменьшения веса и ветровых нагрузок зеркало выполняется:
1.перфорированным
-диаметр отверстия
2.сетчатым
- размер ячейки
Кол-во отверстий определяется из условия Рпр<10%Рпад
Т=Рпр/Рпад- коэфф. прохождения, характеризует эффект.
несплошных антенн.
73. Линзовая антенна
,DH формируются за счет формы линзы.
Линзы подразделяются по способу реализации:
1. диэлектрические;
2. металлопластинчатые;
3. металловоздушные, металлодиэлектрические;
4. диэлектрические дырчатые.
По форме профиля:
1.однопреломляюшая- лучи преломляются на 1 поверхности,
2.двухпреломляющая- лучи преломляются на 2 поверхностях.
Vф≠С условие преломления
Vф<С,n>1- замедляющие линзы(из однородного диэлектрика),
Vф>С,n<1-ускоряющие линзы.
n- const линза однородная, n=f(M), MϵVлинзы- неоднородная
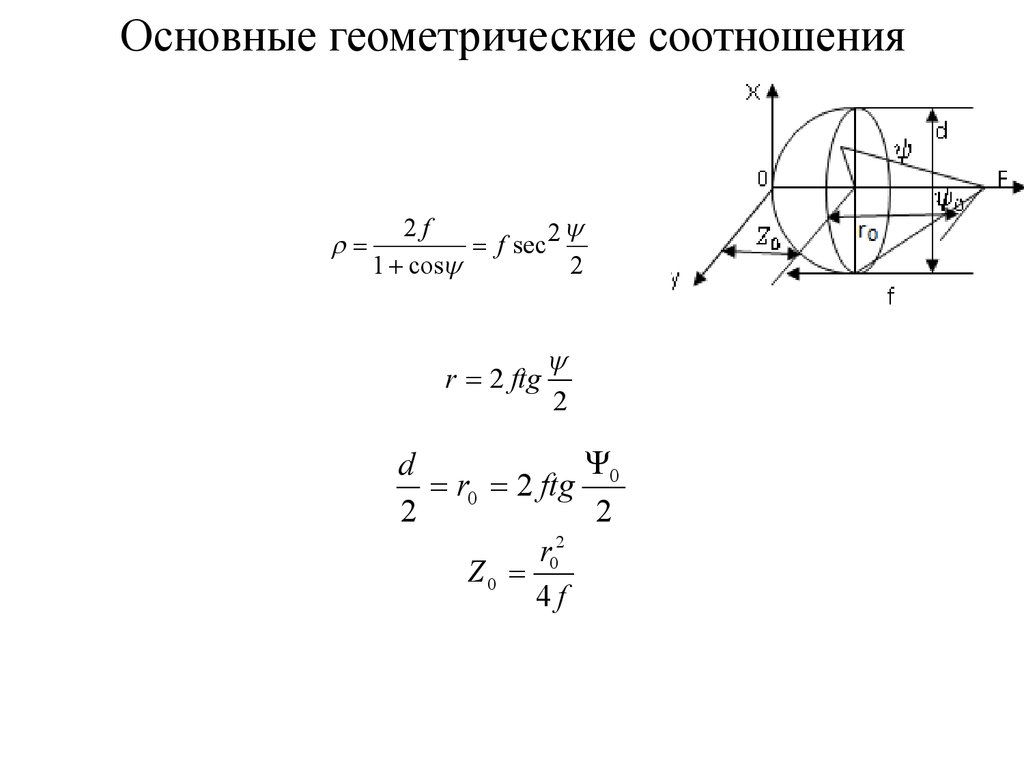
74. Основные геометрические соотношения
Поверхность параболоида образуется за счетвращения параболы вокруг фокальной оси
в декартовой с.к x2+y2=2pz=x2+y2=4fz (1)
в сферической.с.к
2f
2
(2)
1 cos
f sec
2
(3)
Положение точки в раскрыве параболоида вращения
Радиус раскрыва зеркала:
r 2 ftg
2
Глубина зеркала при х=r0
0
d
r0 2 ftg
2
2
r02
Z0
4f
Z0<f
(4)
(5)
(6)
(2ψ0<π)- мелкий параболоид или длиннофокусный
Z0>f (2ψ0>π)- глубокий или короткофокусный
75.
Из условия равенства оптических длин путей луча, падающего налинзу в т.С и луча, идущего вдоль оптической оси до т.О
(7)
(8)
Уравнение профиля линзы:
(9)
n>1 уравнение гиперболы
Направление асимптоты гиперболы:
Угол раскрыва ограничен неравенством:
(10)
76. Ускоряющая линза
n 1f
n cos 1
Уравнение профиля линзы:
(11)
d
n<1- это уравнение эллипса
max
d 2
( f t') ( )
2
2
(12)
Из условия равенства оптических путей
max f nt '
2
( f (/ d )
f /d
t
1
2
2
d
(n 1)
4(n 1) n 1
(13)→
(12а)
1
d
t (
f)
n 2 sin 0
замедляющая линза
1
d
t'
f /d
( f / d )2
1
t' ( f
)
n
2
sin
d 1 n
(1 n) 2 4(1 n 2 ) (14) ускоряющая
0
линза
77. Амплитудное распределение в раскрыве.
ΔХ2x
z
ΔХ1
Приравнивая потоки мощности в пределах угла и отрезка:
P0 ( ) П ( х) X ,
(15)
Переходя к дифференциалам:
Е 2 ( х)
d
П ( x)
Р0 ( )
,
240
dx
(16)
Используя уравнения для замедляющей линзы:
(n 1) sin
x f
,
n cos 1
Дифференцируем обе части по ψ:
d
(n cos x 1) 2
,
dx
f (n 1)(n cos )
(17)
78.
Амплитуда поля в раскрыве:Е ( х) СF0 ( ) A1 ( )
где
C
(18)
240 P0 (0)
постоянный множитель,
f
А1 ( )
1 cos
(1 n)(cos n)
характеризует влияние замедляющей цилиндрической
линзы на АР в ее раскрыве.
АР на теневой поверхности линзы:
E ( x)
А( x)
F0 ( ) A1 ( )
E (0)
(19)
79.
Замедляющая линза:Ускоряющая линза:
1
А1 ( )
n 1
1
А1 ( )
1 n
n cos 1 3 ,
Для зеркальной цилиндрической антенны:
(20)
n cos
1 n cos
cos n
(21)
3
.
учитывая уравнение параболы
2f
,
1 cos
и соотношения
dx
cos (1 cos ) sin sin
2f
2f
2
d
1 cos
(1 cos )
Получаем амплитуду поля
Е(х)=СF0(ψ)A1(ψ),
где
x sin ,
d
dx
cos 2
2
f
А1( ) cos A( x) F0 ( ) A1 ( )
2
cos 2
(22)
f
2
80. Методика расчета DH ЗА и ЛА
Поле антенны в дальней зоне:Е ( Р ) Е 0 ( Р ) f сист ( , ),
(23)
Множитель системы, раскрыв синфазный φ(r,α)=0:
f сист (
2 r0
j ( r , ) jkr sin cos( )
(24)
A
(
r
,
)
e
e
rdrd
0 0
DH облучателя осесимметричная, АР не зависит от α
r0
(25)
f сист ( ) 2 А(r ) J 0 (kr sin )rdr ,
0
Приближенный метод расчета:
n
jkr sin
F
(
)
A
(
r
)
e
dr ,
А(r ) i Ai (r ), i
i
n
1
F ( ) i Ai (r )e
L 1
jkr sin
L
n
dr i Ai (r )e
1
L
jkr sin
n
dr i Fi( )
1
(26)
81.
косинусоидальное82. Оптимальные соотношения параметров в ЛА и ЗА
Параметры:ширина DH облучателя -2θ0,5обл,
фокусное расстояние-f,
размер раскрыва антенны- d,
угол раскрыва -2ψ0
2
E ( 0)
Рассчитаем КНД: D E 2 ,
0
P P 0
(27)
Амплитуда поля в главном направлении Е(0):
E (0) E 0 (0) f сист (0)
где амплитуда поля центрального
1 cos
Е 0(0) Emax
излучателя Гюйгенса:
2 R
Учитывая:
0
60 PD
0
Σ
Rf
E (r , ) F0 ( , )
A(r , )
,
E (0)
f
(28)
(29)
83.
rdr2
2 f tg d ,
f
2
2
f sec
r 2 ftg ,
2
2 2
находим:
f сист (0) 2 f
2
0
0 F0 ( , )tg 2 d dx
0
(30)
подставляя 29,30 в 28 получаем амплитуду поля направленной антенн
2 0
2f
(31)
E0
60 P D0 F0 ( , )tg d dx
R
2
0 0
Амплитуда поля изотропной антенны:
E0
Используя 31, 32 имеем
D0
4 4 f
D 2
S0
2
r0
4 2
2
2 0
0
где S0=πr0- площадь раскрыва
60 P
(32)
R
0 F0 ( , )tg 2 d d
2
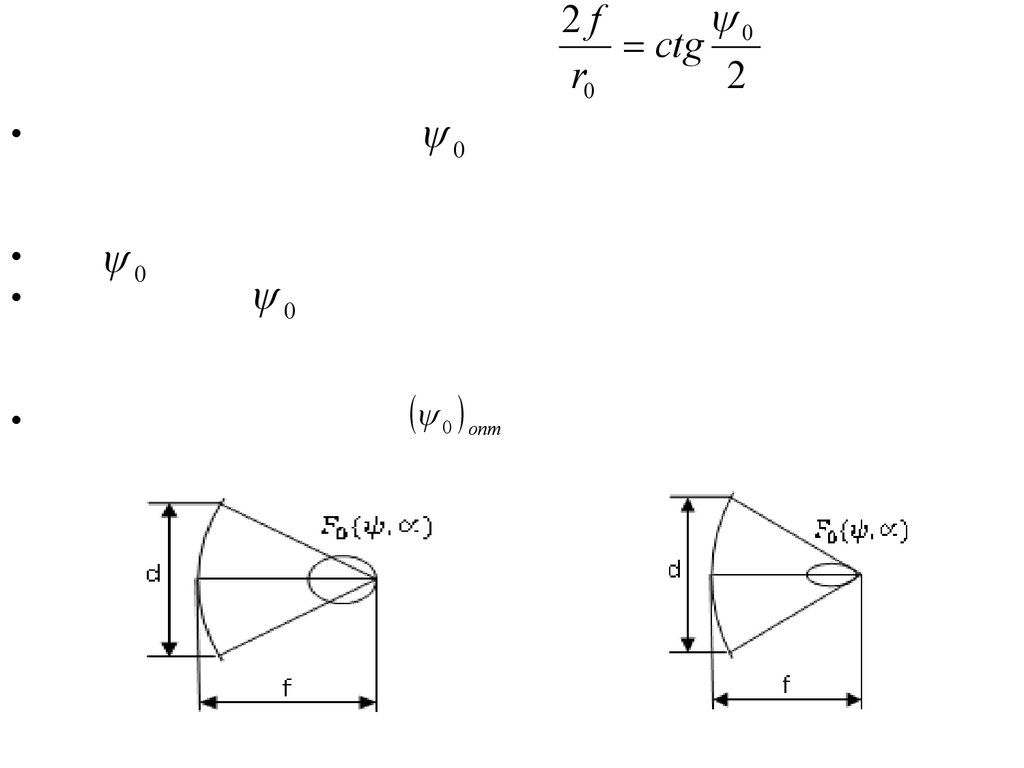
84.
2f0
ctg
,
Учитывая:
r0
2
D0
4
(33)
2 0
2
F
0 ( , ) sin d d
в направлении мах
КНД параболоида вращения: 0 0
2
2 0
ctg 2 0 F0 ( , )tg 2 d d
0 0
4
2
D 2 S0
2
2
F
0 ( , ) sin d d
(34)
0 0
2 0
F0 ( , )tg d d
2 0
ctg
2
0 0
2
КИП А
2
2
F
0
( , ) sin d d
2
(35)
0
F0 ( )tg d
При осесимметричной DH облучателя:
2
0
2 0
КИП А 2сtg
2 2
КИП параболоида вращения зависит от DН
F0 ( ) sin d
0 0
облучателя и угла раскрыва зеркала.
0
2
85.
КИПА зависит от :• доли мощности, излученной облучателем, перехватываемой зеркалом
•эффективности использования излучающего раскрыва
(36)
КИПА = γηп
2
S эфф
S0
A(r , )ds
1 S0
1 2f
2
S 0 A (r , )ds
r0
S0
2
d d
2 F0 ( )tg
2
0 0
2
0
(37)
F0 ( ) sin d d
2 0
0 0
коэффициент перехвата - ηп
2 0
п
P пер
P
2
F
0 ( , ) sin d d
0 0
2
F
2
0
0 0
( , ) sin d d
(38)
86.
Перемножая (37),(38) и учитываяполучаем соотношение (35)
0
2f
ctg
r0
2
• При малых значениях
0 раскрыв облучается равномерно
(γ→1) , доля энергии облучателя «выливается» за края
раскрыва зеркала (ηп мало) рис.1а
• С ↑ 0 ηп ↑, но величина γ ↓.
• При больших 0 энергия облучателя перехватывается
зеркалом (ηп→1) , но раскрыв используется неэффективно
(значение γ мало) рис.1б
• Оптимальное значение 0 опт соответствует спаду поля
облучателя к краям зеркала примерно на 9 – 10 дБ.
а
Рис.1
б
87.
Ширина DH2 0,5 р
65...70
(39)
d
УБЛ Fб1=-(22…24)дБ
максимум КИПА=0,83
Реально КИПА = 0,6…0,7 в лучших образцах 0,75
• не учет поля поперечной поляризации,
• рассеяние энергии на облучателе, элементах конструкции,
теневой эффект облучателя,
• влияние антенного обтекателя,
• фазовые искажения в раскрыве (деформация зеркала ,
отклонения фронта волны от сферического и т.д).
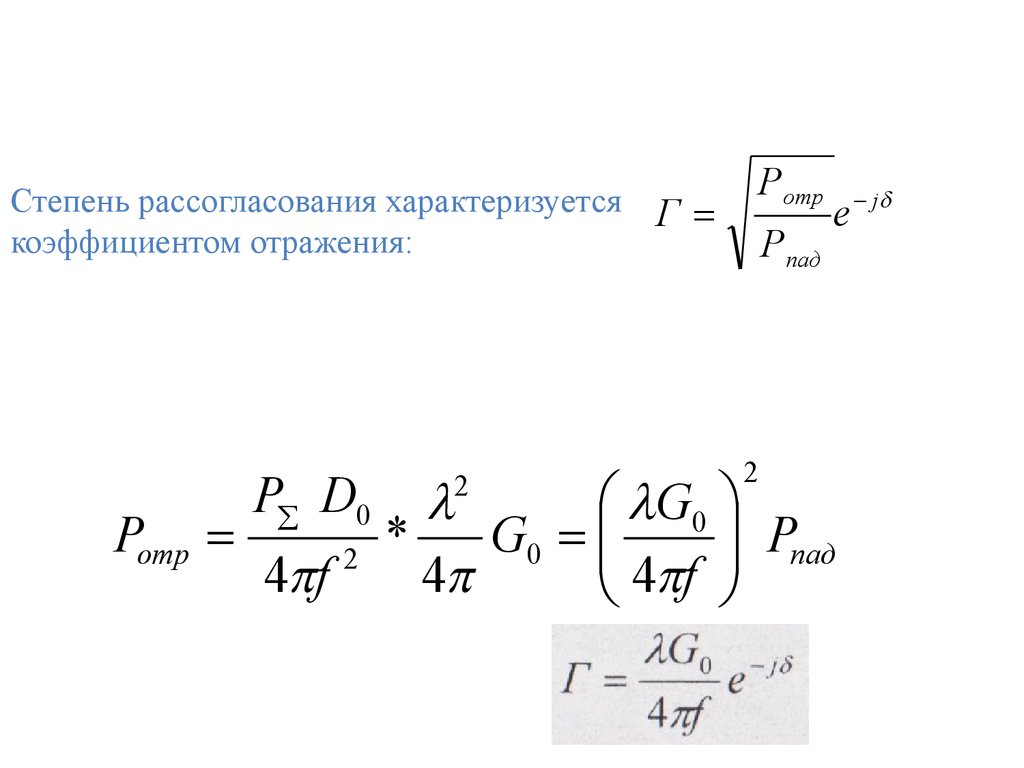
88.
Реакция зеркала на облучательОблучатель- влияет на УБЛ DН и КНД антенны.
Зеркало-влияет на работу облучателя в части рассогласование облучателя с
фидером за счет приема части энергии, отраженной от зеркала.
Степень рассогласования характеризуется
коэффициентом отражения:
Г
Ротр
Рпад
e j
Ротр-мощность отраженной волны в фидере,
Рпад-мощность падающей волны=мощности, подводимой к
облучателю,
δ-фаза коэффициента отражения.
Pотр
P D0
4 f
2
2
G0
Pпад
*
G0
4
4 f
2
D0, G0- максимальные КНД и КУ
с ↑ f влияние зеркала на
облучатель усиливается
(43)
89.
Для уменьшении реакции зеркала на облучательиспользуются способы:
• вынос облучателя из поля отраженной волны (рупорно
параболической антенны);
• использование облучателя с круговой поляризации поля;
• использование согласующей пластины, устанавливаемой
вблизи вершины параболоида, размеры и расположения
которой подбираются так, чтобы отраженное ею поле
компенсировало у облучателя поле, отраженное зеркалом.
90.
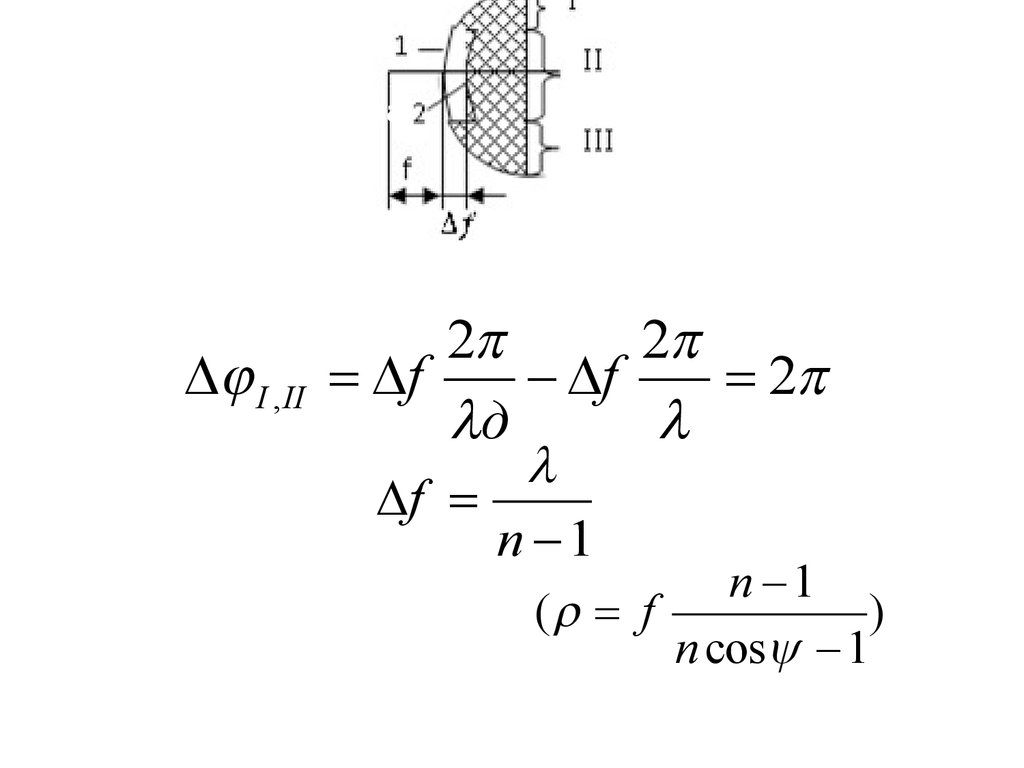
Замедляющая линзаЗонирование ЛА- ↓толщины линзы в пределах некоторых участков
ее поверхности-зон. Разность фаз в I и II областях равна или кратна
2π.
(44)
Выбираем:
I , II
Разность хода вдоль
фокальной оси:
2
2
f
f
2
д
f
n 1
n 1
( f
)
n cos 1
Определив f2=f1+Δf, то по формуле
профиля замедляющей линзы,
можно рассчитать профиль линзы во II зоне.
(45)
91.
уравнение профиля к-й зоны:n 1
n 1
(k 1) (n 1) f1 (k 1)
k
fk
f1
n cos 1
n cos 1
n 1
n cos 1
Максимально возможное число зон N на единицу больше
целой части выражения
t
t (n 1)
f
Зонирование в ускоряющей линзе.
(1 n) f 1 (k 1)
k
1 n cos
(46а)
(46)
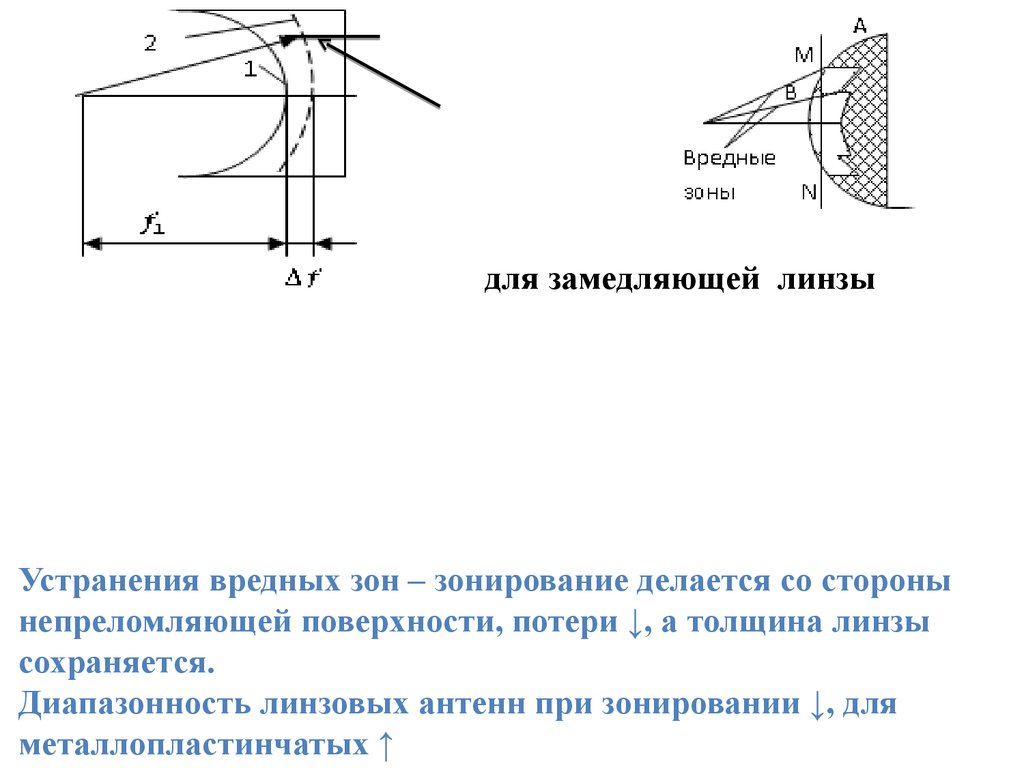
92.
Вредные зоныдля ускоряющей линзы:
вредные зоны-сектора, в
пределах которой энергия
облучателя рассеивается.
для замедляющей линзы
вредные зоны-«неосвещенные»
участки на апертуре линзы.
АР в раскрыве имеет провалы,
приводящие к появлению
дополнительных БЛ и ↓ КНД
антенны.
Устранения вредных зон – зонирование делается со стороны
непреломляющей поверхности, потери ↓, а толщина линзы
сохраняется.
Диапазонность линзовых антенн при зонировании ↓, для
металлопластинчатых ↑
93.
Отражение электромагнитных волн от поверхности линзыпроисходит:
• от обеих её поверхностей, т.к. n отличается от коэффициента
преломления окружающего пр-ва .
• от преломляющей (освещенной) поверхности ↑БЛ и искажает
АФР в раскрыве.
Энергия отраженная от линзы рассогласовывает облучатель с
фидером.
Для нормального падения коэффициент отражения:
n 1
Г
n 1
определяется функциями Френеля,
зависит от поляризации падающей волны,
угла падения ,
величины n.
n 1
отр 8,69(
n 1
)
2
94.
Для ↓отражения используют « просветляющие слои», аналогчетвертьволновых согласующих трансформаторов.
tс=0,25λ-толщина слоя при нормальном падении;
λс= λ/nc длина волны в слое,
nc=√n-толщина слоя при нормальном
падении
94
95. Симметричный вибратор
Лекция 896. ПРЯМОЛИНЕЙНЫЙ ПРОВОД, В СЕРЕДИНЕ КОТОРОГО ВКЛЮЧЕН ИСТОЧНИК ПЕРЕМЕННОЙ ЭДС. ПОД ЕЕ ДЕЙСТВИЕМ ПО ПРОВОДУ ТЕЧЕТ ПЕРЕМЕННЫЙ ТОК, ВОЗБУЖДАЮЩИЙ
ПРЯМОЛИНЕЙНЫЙ ПРОВОД, В СЕРЕДИНЕ КОТОРОГО ВКЛЮЧЕНИСТОЧНИК ПЕРЕМЕННОЙ ЭДС. ПОД ЕЕ ДЕЙСТВИЕМ ПО ПРОВОДУ
ТЕЧЕТ ПЕРЕМЕННЫЙ ТОК, ВОЗБУЖДАЮЩИЙ ЭЛЕКТРОМАГНИТНОЕ
ПОЛЕ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ.
.
Поле и DH
E
S ( r a )
0
Рассмотрим тонкий вибратор
а l ,
Допустимые предположения:
е
J
• Поверхностные электрические токи
Z и эквивалентные
магнитные токи заменяются расположенной на оси вибратора
бесконечно тонкой нитью продольного электрического тока,
2 aJ ЭZ ( z )
считающегося непрерывной функциейI Zв(Z)
области
возбуждающего зазора и обращающегося в нуль на концах
вибратора:
I Z (l ) I Z ( l ) 0
(1
97.
• Еzr ( z )создаваемая током I z (z ) на боковойповерхности воображаемого идеального проводника(вибратора),
охватывающего нить тока равна нулю всюду, за исключением
области возбуждающего зазора шириной.
Еz ( z)
z b
2
,b
EB ( z )
2
- возбуждающая функция при
функция
E B ( z ) const
b l ,
98.
где2
1
d
Az
2
EZ
(k Az
)
2
j
dz
вибратор
k -волновое число среды, окружающей
;
(2)
- абсолютная диэлектрическая проницаемость.
Линейное дифференциальное уравнение второго порядка
для векторного потенциала на боковой поверхности
вибратора.
b
0
при
z
d Az
2
2
k
A
z
b
dz 2
j EB ( z )при z
2
2
Решение в общем виде ∑ общего решения однородного
уравнения и какого либо частного решения неоднородного
уравнения,
b
Az ( z )
C1 jkz C 2 jkz
e
e
4
4
(3)
z
2
j jkz
jkz
jkz
jkz
e
E
(
z
)
e
d
z
e
E
(
z
)
e
d
z
B
B
2 jk
b
z
2
(4)
b b
Z ,
2 2
99.
Функцию распределения тока:1 l
e jkr
Az z
I z ( z )
dz
(5)
4 z l
2
где r ( z z ) 2 a 2 - расстояние между точкой расположения источника
.
и точкой
наблюдения.
1
k
z
Учитывая что:
Интегральное уравнение Галлена для неизвестной функции распределения тока
l
I z ( z ) K ( z z )dz C1e jkz C 2 e jkz
z l
К ( z z )
Если
b
вычисляются:
, то E B ( z ) const
e
b
z
2
2 jkz
jkz
jkz
jkz
e
E
(
z
)
e
d
z
e
E
(
z
)
e
d
z
B
B
b
z
z
2
jk ( z z ) 2 a 2
(6)
( z z ) 2 a 2
и определенные интегралы в (6)
b
2
jkz
E
e
B dz E B b
b
z
2
(7)
100.
Вибратор возбуждается идеальным генератором напряжения с Rвнутр=0;согласно закону Кирхгофа:
(9)
E
b
Э
B
l
I z ( z ) K ( z z )dz C1e
l
“-“ относится к области z
“+” – к области
z
b
2
jkz
C2e
jkz
2 Э jkz
e
z
(10)
b
2
2 Э e jkz z 0 2 Э
(cos kz j sin k z )
jkz
z e z 0
z
Разлагая С1 и С2 по формуле Эйлера, вводя переменные С3,С4.
Получаем уравнение Галлена:
2 Э
sin k z
I z ( z )K ( z z )dz C3 cos kz C4 sin kz j
z
l
l
где С4=0
(12)
Для симметричного вибратора:
l
I z ( z ) I z ( z )
Az ( z ) Az ( z )
I z ( z ) K ( z z )dz C cos kz j
l
2 Э
sin k z
z
(13)
101.
Резонансный характер в окрестностиK ( z z ) K (
cos kr
sin kr
j
),
kr
kr
z z
r ( z z ) 2 a 2
векторный потенциал нити электрического тока
на боковой поверхности вибратора определяется
токами, текущими в близи точки
z z
Интегрирование
от
до
z z h
z z h
e
I z ( z)
jk ( z z ) 2 a 2
z z h, z h
, где
h
1
I z ( z)
z z
z h
e jkr
dz
a2 h2 h
2h
I
(
z
)
d
z
I
(
z
)
I
(
z
)
ln
I
(
z
)
2
ln
z
z
z
z
2
2
2
2
r
a
l
z h ( z z ) a
a h h
l
обозн
(14)
(15)
102.
r ( z z ) 2 a 2a 0 выражение (15)
2 Э
I z ( z ) Q C3 cos kz C 4 sin kz j
sin k z
z
(16)
Граничные условия I z (l1 ) 0, I z ( l 2 ) 0 находим:
4 Э sin kl1 sin kl2
С3 j
z sin k (l1 l2 )
2 Э sin k (l1 l2 )
С4 j
z sin k (l1 l2 )
(17)
103.
sin(l1 z )I z ( z) b I 0
,
z
sin kl1
2
sin(l2 z )
I z ( z)
I
,
b
0
z
sin kl2
2
I0 j
4 Э sin kl1 sin kl2
zQ sin k (l1 l2 )
(18)
величина тока в точках возбуждения
Для симметричного вибратора распределение тока получается
симметричным относительно середины:
I z ( z) I 0
sin k (l z )
(19)
sin kl
Для комплексной амплитуды поля вибратора
E E 0 f сист ( )
E j 60 I вх sin e jkr
0
r
(20)
l
f сист ( ) A( z )e j ( z ) kz cos dz
l
(21)
104.
АФР тока в системеA ( z ) A( z )e
j ( z )
I z ( z ) sin k (l z )
I вх
sin kl
l
1 0
jkz cos
jk 2 cos
f сист ( )
dz sin k (l z )e
dz
sin k (l z )e
sin kl l
0
2 cos(kl cos ) cos kl
f сист ( )
k sin kl
sin 2
105.
E 60 I п e jkr cos(kl cos ) cos klr
sin
Амплитуда поля:
E 60 I п e jkr cos(kl cos ) cos kl
r
sin
DH отнесенная к пучности тока:
cos(kl cos ) cos kl
f ( ) 60
sin
2l 5
при
4
max DH
2
(22)
(23)
(24)
f max 60(1 cos kl )
Нормированная DH:
1
cos(kl cos ) cos kl
F ( )
1 cos kl
sin
(25)
Для полуволнового вибратора
cos kl 0
cos( cos )
2
F ( )
sin
при 2l
2
2 0,5 P 78 o
(26)
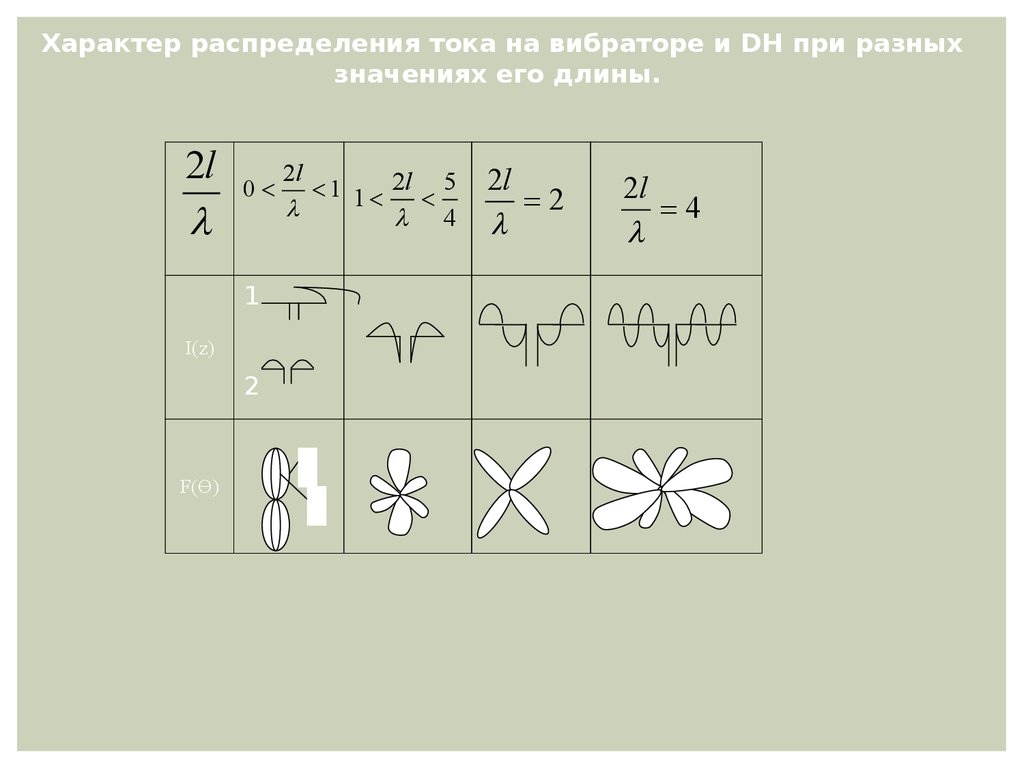
106.
Характер распределения тока на вибраторе и DH при разныхзначениях его длины.
2l
0
2l
1 1 2l 5
4
1
I(z)
2
F(Ө)
1
2
2l
2
2l
4
107. Сопротивление излучения и KHD
RСопротивление излучения и KHD
cos( kl cos ) cos kl 2
1 2 2
f ( , ) sin d d 60
d
120
0 0
0
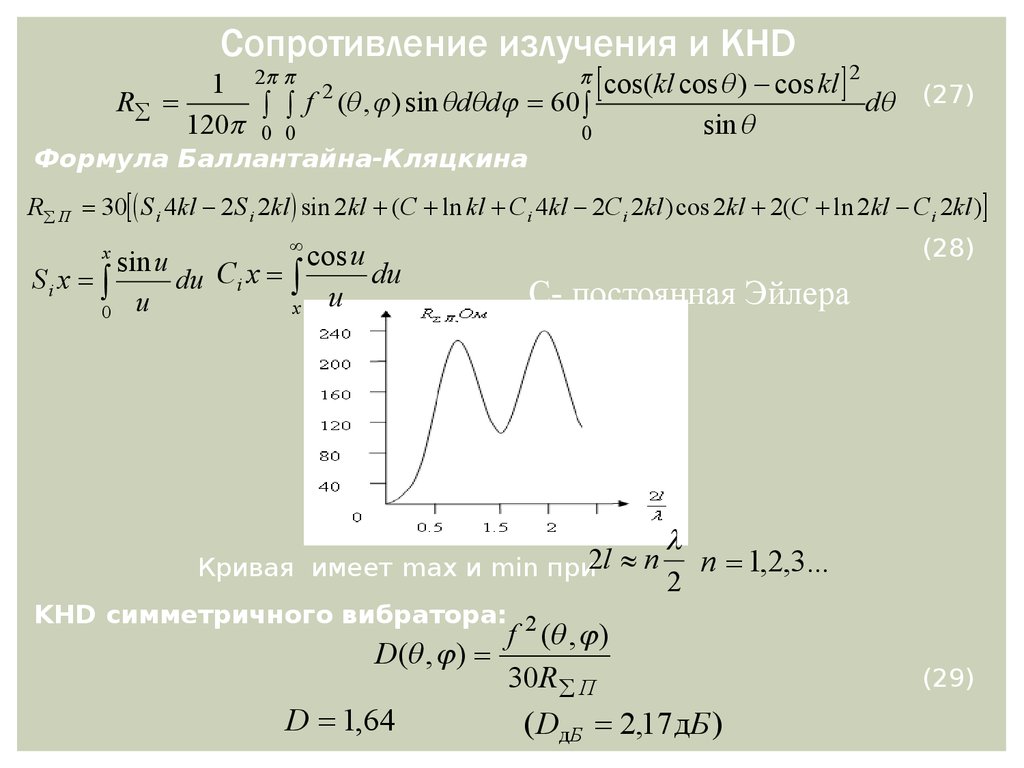
Формула Баллантайна-Кляцкина
sin
(27)
R П 30 S i 4kl 2S i 2kl sin 2kl (C ln kl Ci 4kl 2Ci 2kl ) cos 2kl 2(C ln 2kl Ci 2kl )
cos u
sin u
C
x
Si x
du i
u du
x
0 u
x
(28)
С- постоянная Эйлера
Кривая имеет max и min при2l n
n 1,2,3...
2
KHD симметричного вибратора: 2
D( , )
D 1,64
f ( , )
30 R П
( DдБ 2,17 дБ )
(29)
108. Входное сопротивление
При разведении проводов погонные параметры её в разныхсечениях различны, имеем Z ВХ jZ В ctgkl
линию с переменными параметрами. Эквивалентное волновое
сопротивление.
Z ВЭ 120(ln
0,577)
a
Для тонких проводов:
а
(10 2...10 4 )
Z ВХ R ВХ jZ ВЭ ctgkl
Z ÂÝ (300...1000)Î ì
R П
2
sin kl
jZ ВЭ ctgkl
R П
Z ВX
j (42,5 Z ВЭ ctgkl )
2
sin kl
109.
Для 2вибратора
Z ÂÕ (73,1 j 42,5)Î ì
Для получения чисто активного входного
сопротивления используют укорочения вибратора:
Z ВЭ ctgkl 42,5
l
ctgkl ctgk (
4
4
) ctg (
42,5
2 Z ВЭ
2
k ) tgk k
27
%
100%
Z ВЭ
4
С ↑ толщины провода ↓
110. Возбуждение симметричного вибратора
задача согласованиясимметрирования
задача
Согласование
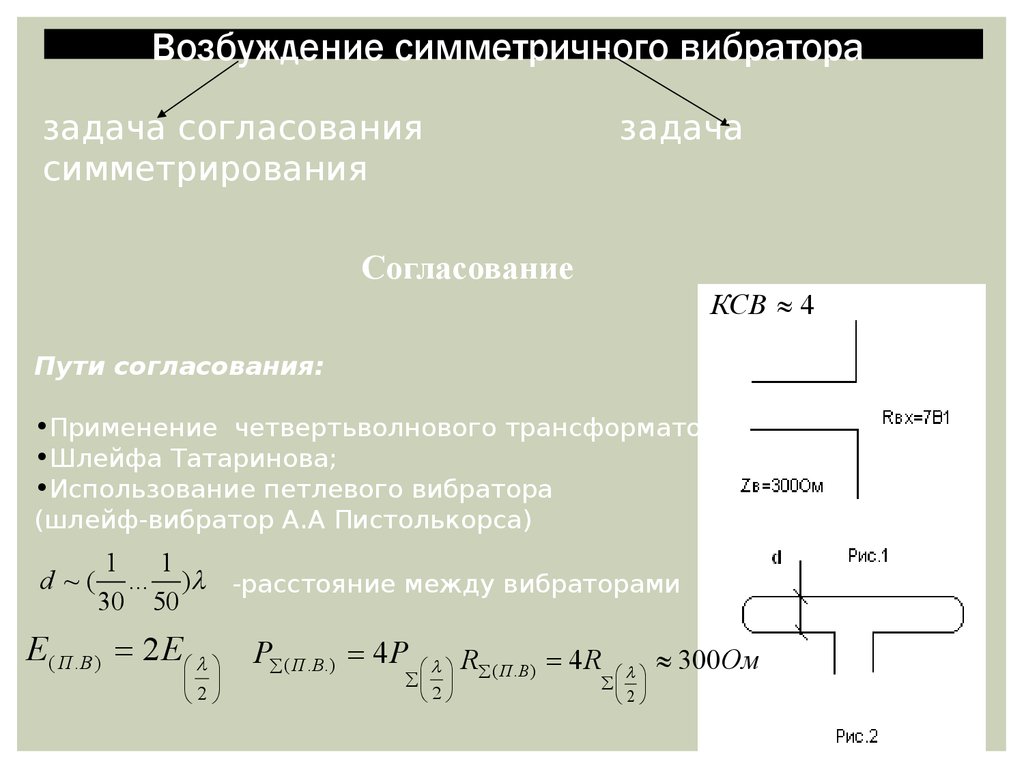
КСВ 4
Пути согласования:
•Применение четвертьволнового трансформатора;
•Шлейфа Татаринова;
•Использование петлевого вибратора
(шлейф-вибратор А.А Пистолькорса)
d ~(
1
1
... ) -расстояние между вибраторами
30 50
Е ( П . В ) 2 Е P ( П .В.) 4 P
2
2
R ( П . В ) 4 R
2
300Ом
111. Симметрирование
При подключении вибратора к коаксиальной линиивозникает асимметрия токов в плечах вибратора, ток,
текущий по правой половине вибратора ответвляется на
внешнюю «оплетку» наружного проводника фидера через
емкость Спар, возникает паразитное поле излучения. Условный
фазовый центр вибратора смещается, DH зеркальной антенны
отклоняется.
Устранение асимметрии токов:
•четвертьволновый стакан
+ простота конструкции, возможность
управления асимметрией тока путем смещения
стакана и
соответственно управления
величиной отражения
DH зеркальной или линзовой антенной с
вибраторным облучателем.
-узкополосность, громоздкость в метровом
диапазоне волн
•U-колено;
•симметрирующая приставка;
•симметрирующая щель.
112. Спиральные антенны с вращающейся поляризацией поля
СПИРАЛЬНЫЕ АНТЕННЫС ВРАЩАЮЩЕЙСЯ
ПОЛЯРИЗАЦИЕЙ ПОЛЯ
Лекция 10
113. Спиральные антенны с вращающейся поляризацией поля
СПИРАЛЬНЫЕ АНТЕННЫ С ВРАЩАЮЩЕЙСЯПОЛЯРИЗАЦИЕЙ ПОЛЯ
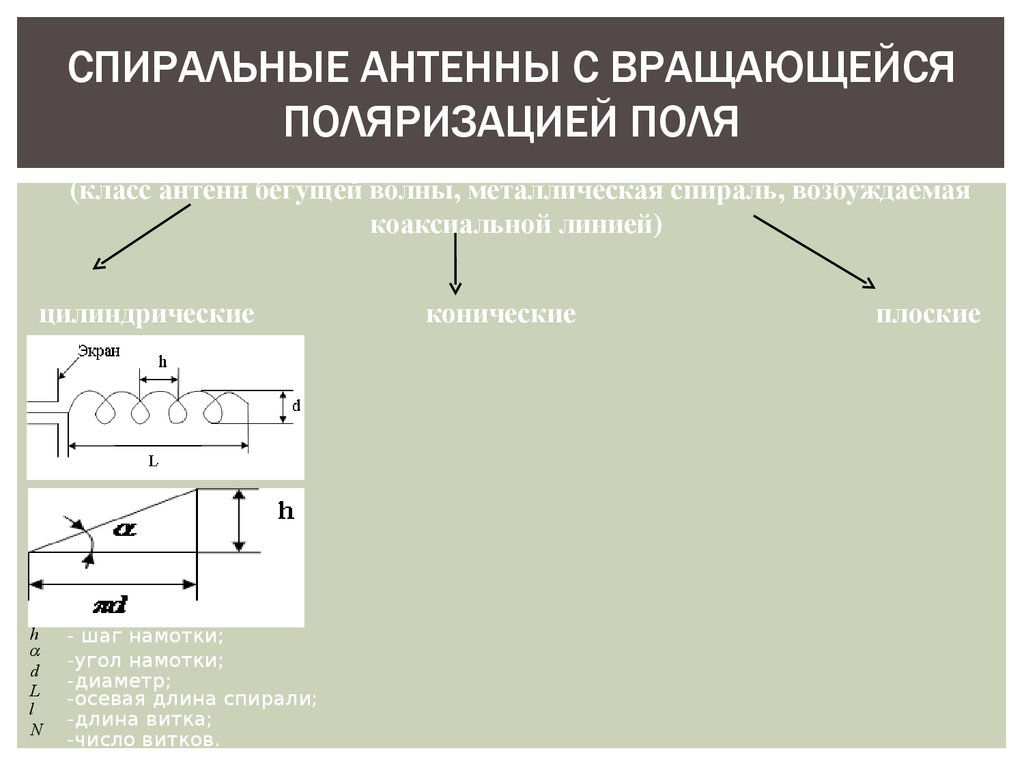
(класс антенн бегущей волны, металлическая спираль, возбуждаемая
коаксиальной линией)
цилиндрические
h
d
L
l
N
- шаг намотки;
-угол намотки;
-диаметр;
-осевая длина спирали;
-длина витка;
-число витков.
конические
плоские
114.
hC
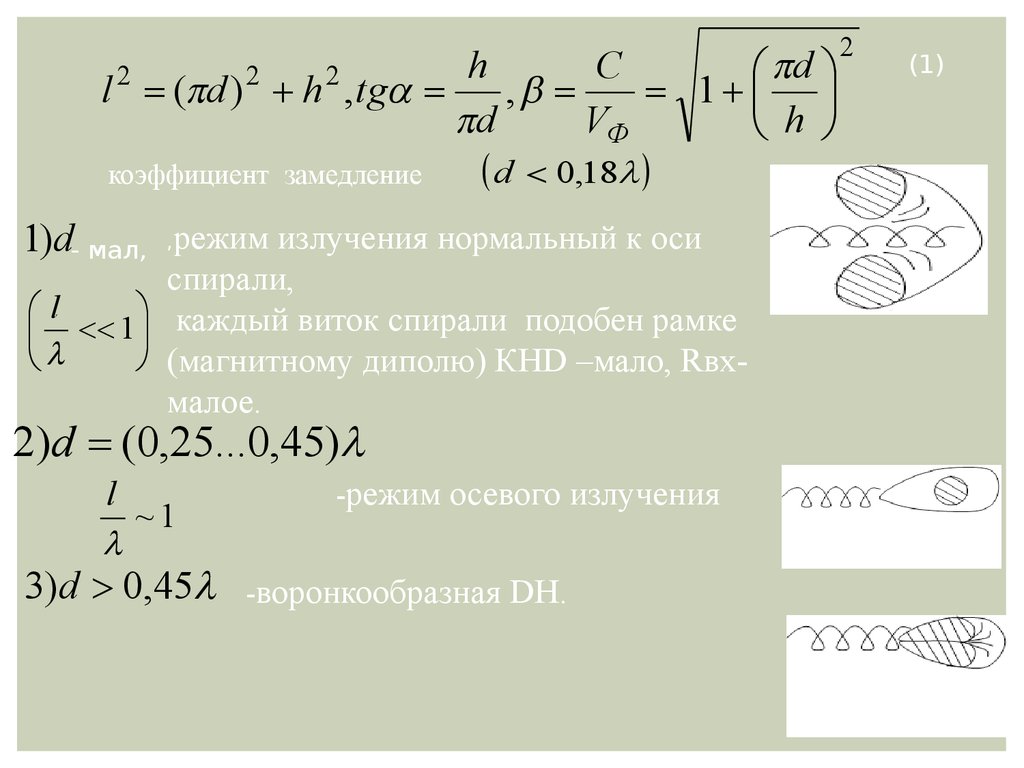
d
l ( d ) h , tg
,
1
d
VФ
h
2
2
2
коэффициент замедление
d
0,18
1)d- мал, ,режим излучения нормальный к оси
l
1
спирали,
каждый виток спирали подобен рамке
(магнитному диполю) КНD –мало, Rвхмалое.
2)d (0,25...0,45)
l
~1
-режим
осевого излучения
3)d 0,45 -воронкообразная DH.
2
(1)















































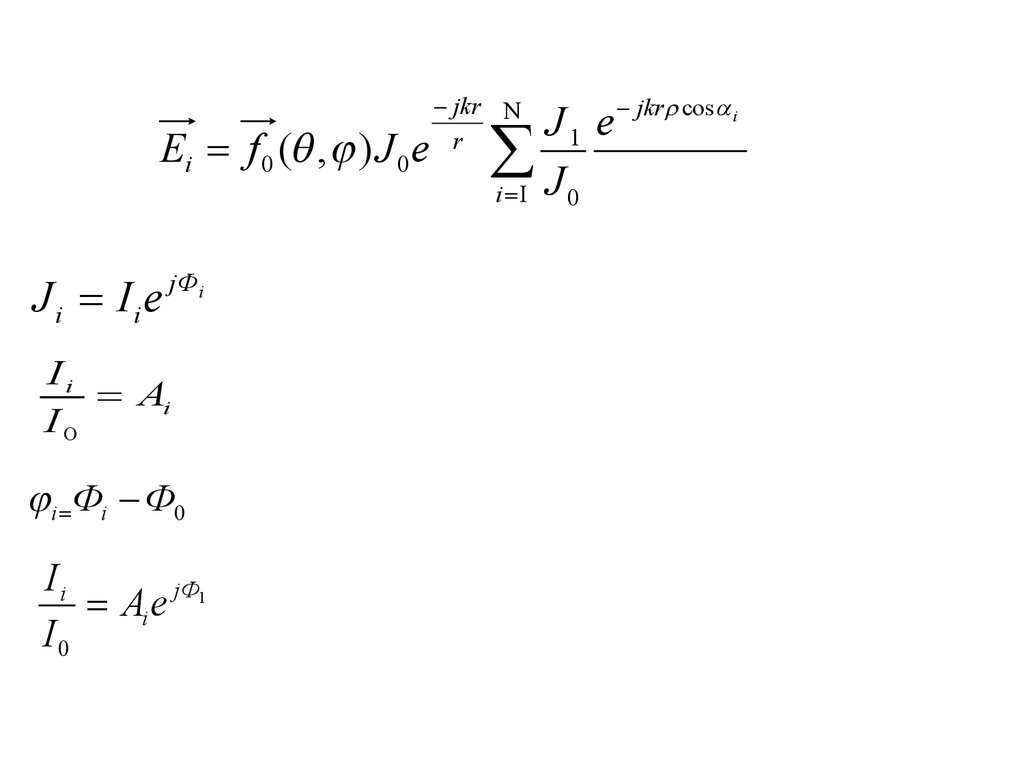
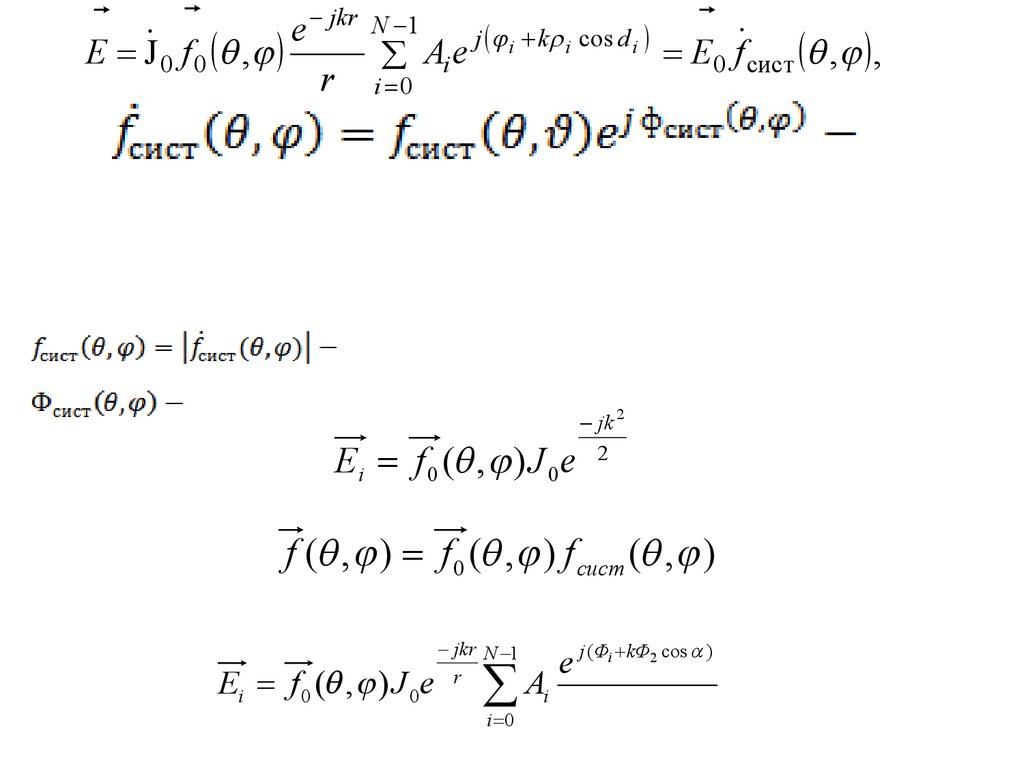






















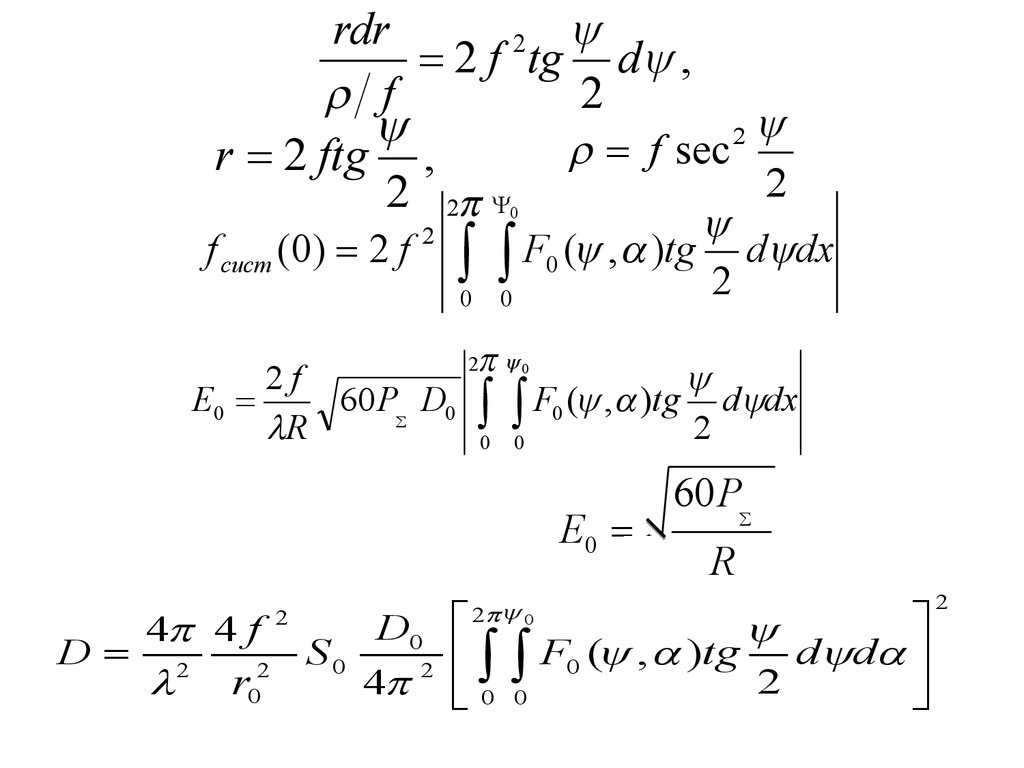




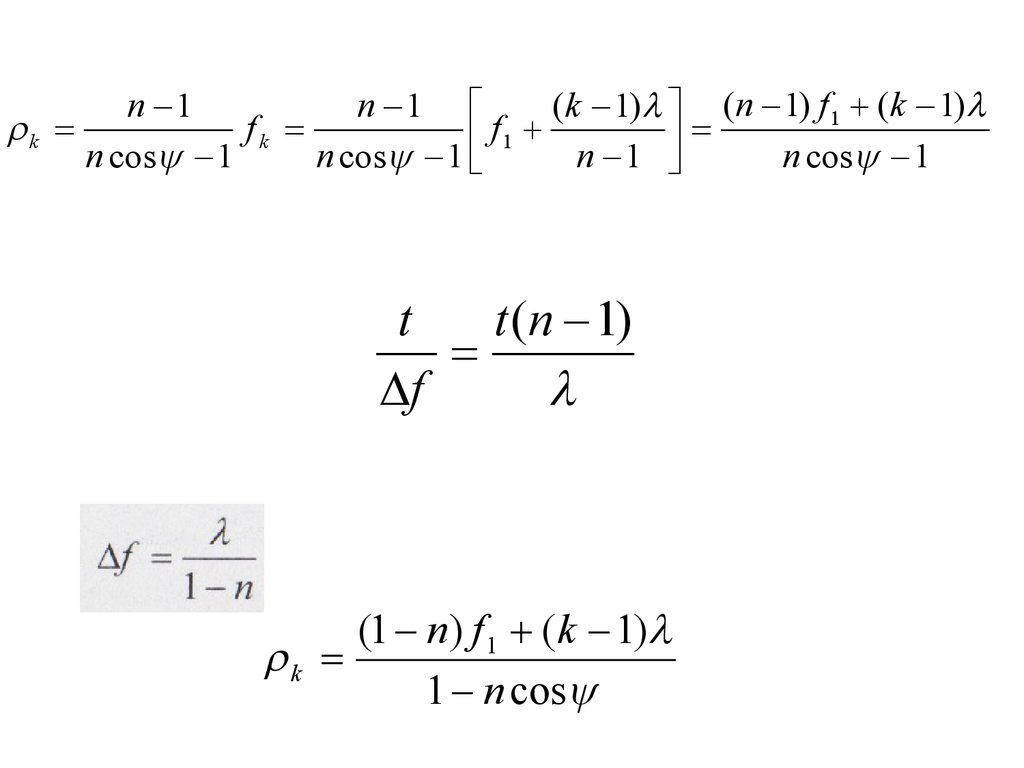


















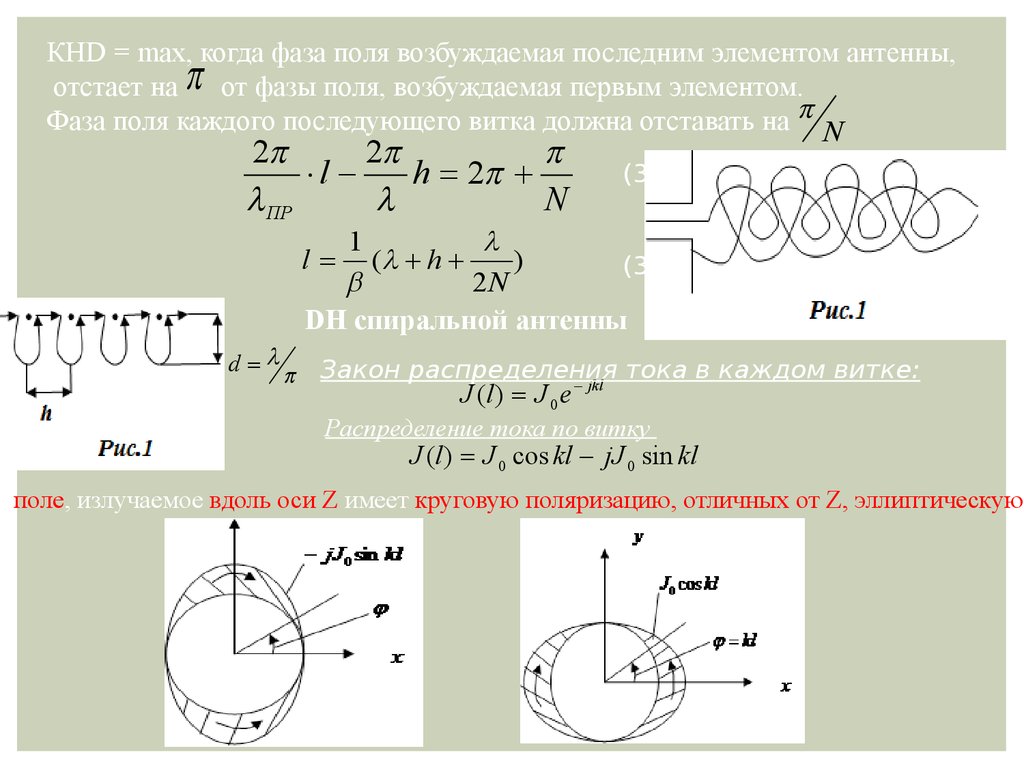

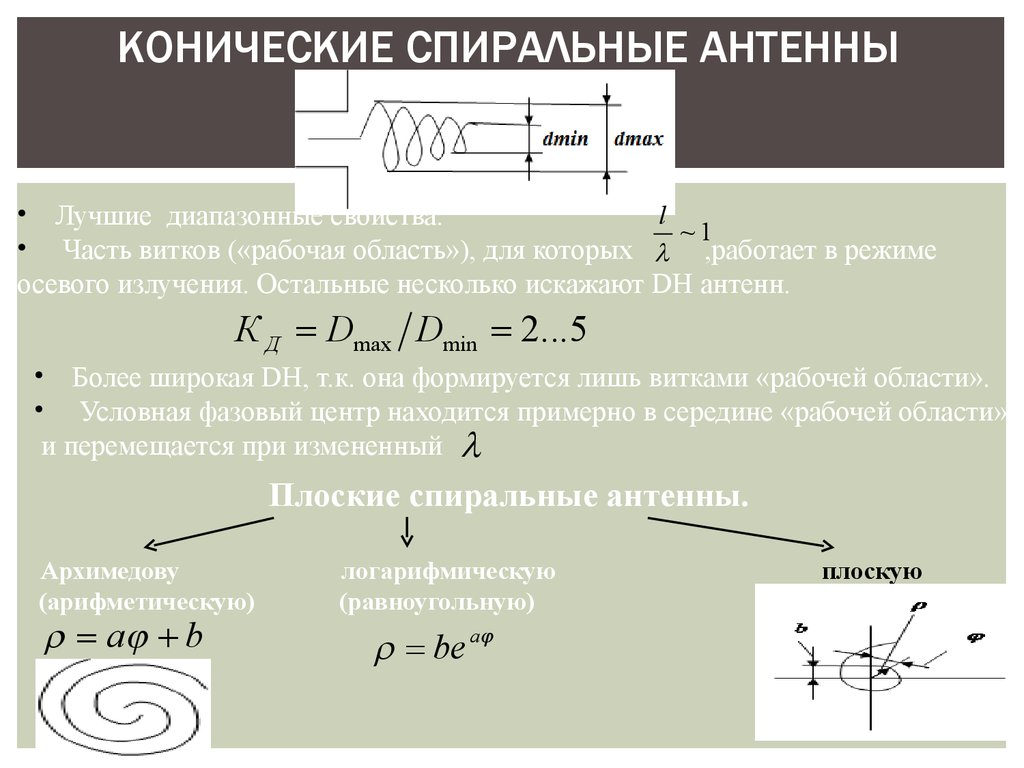





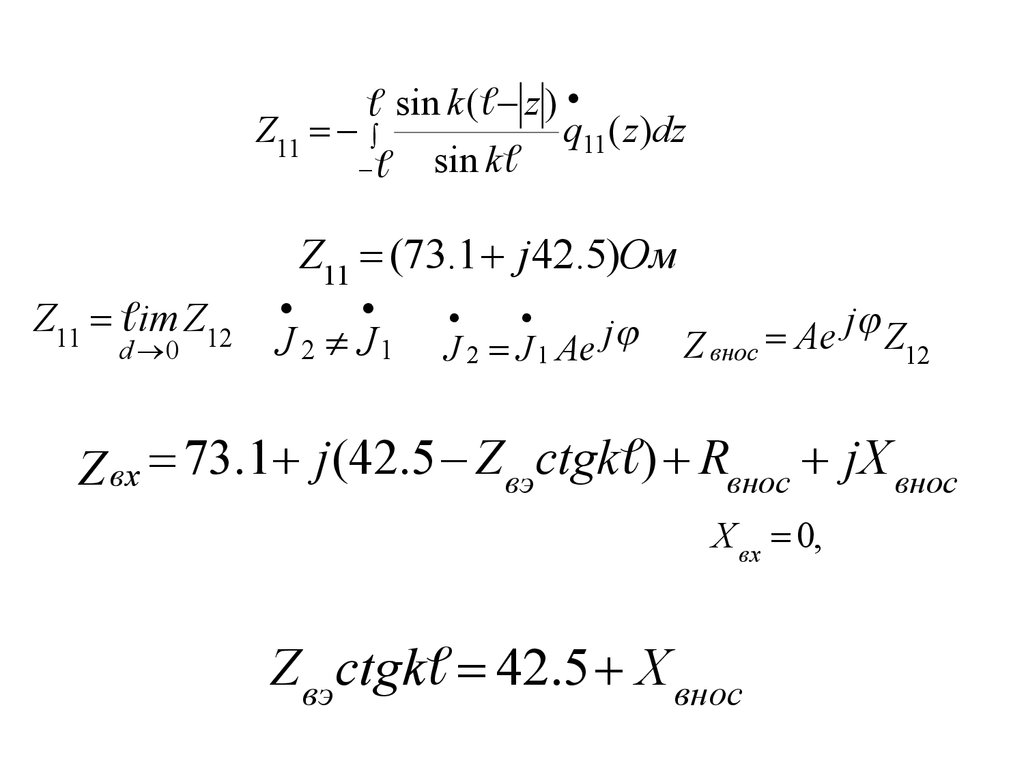
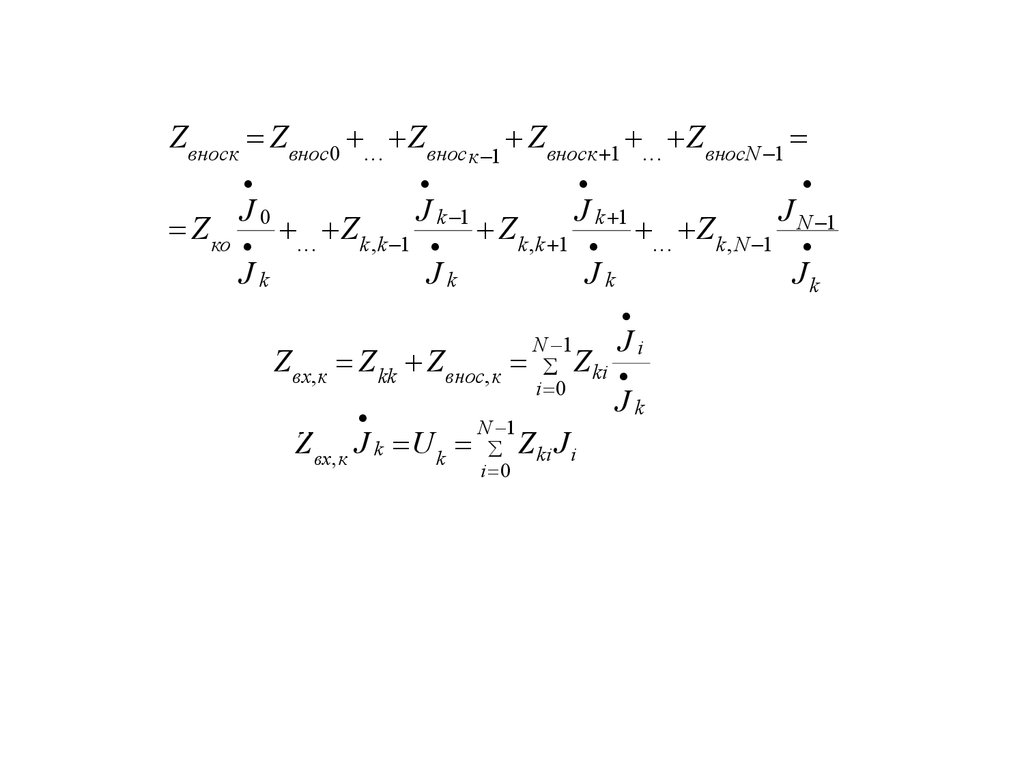

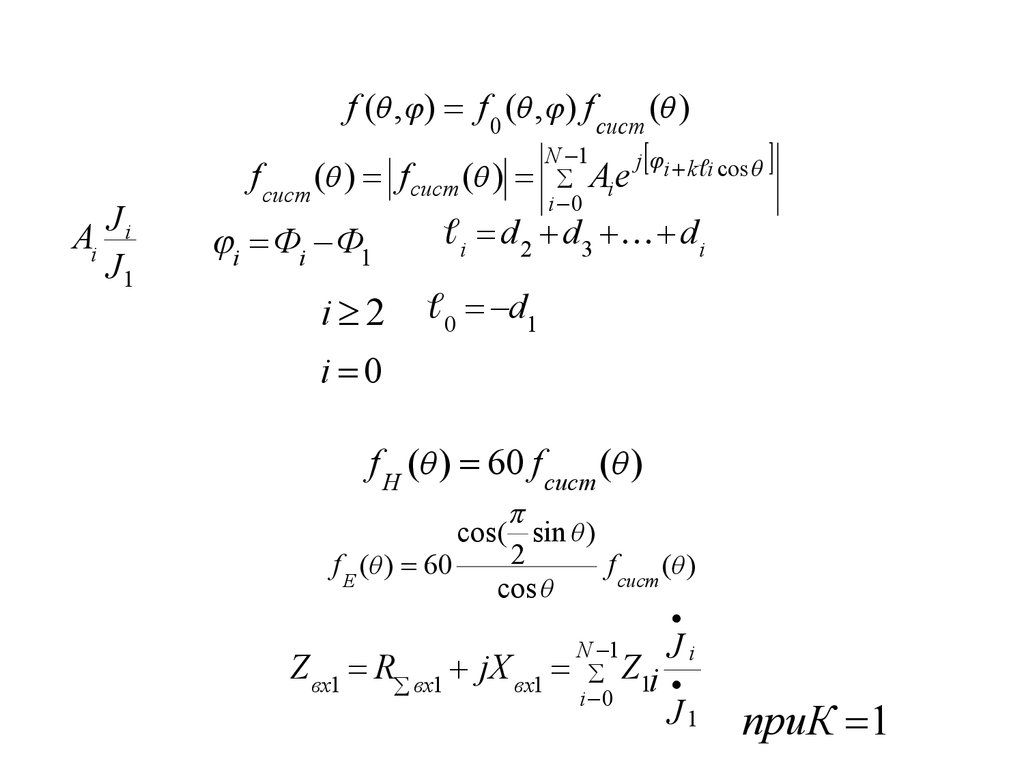
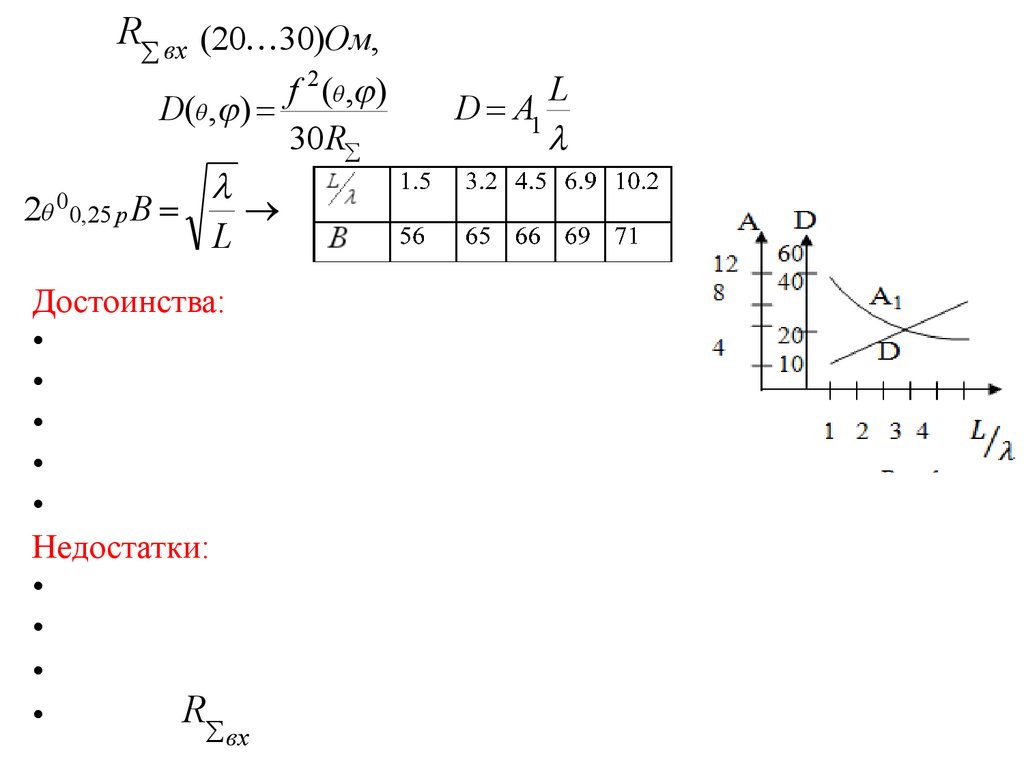
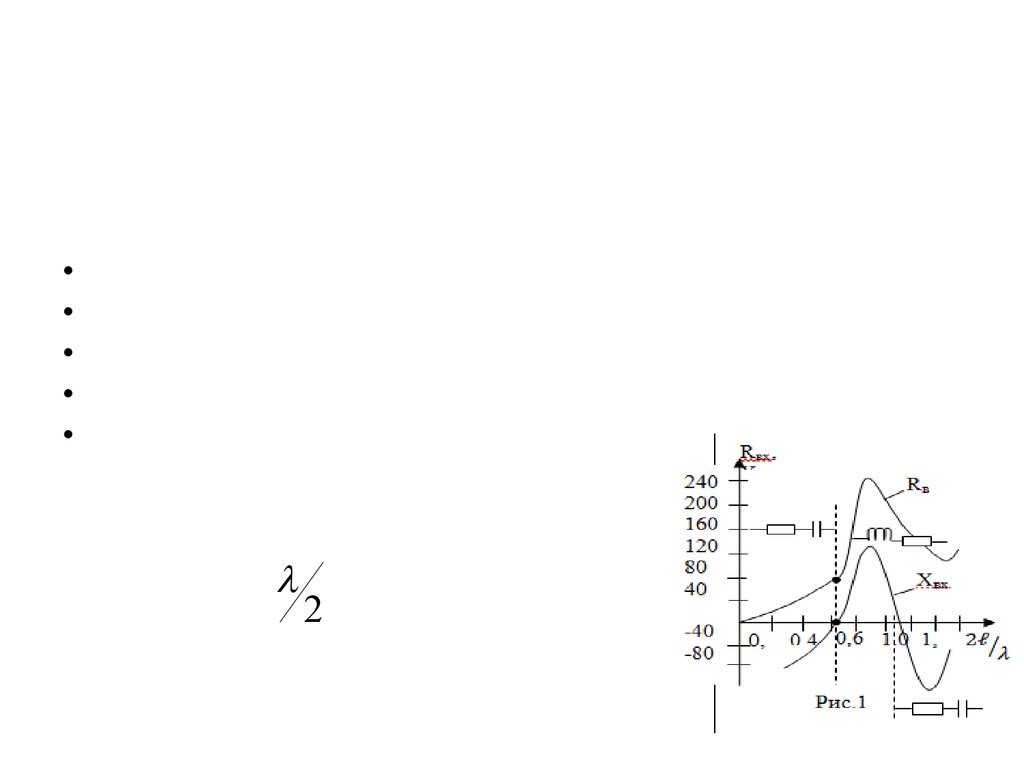
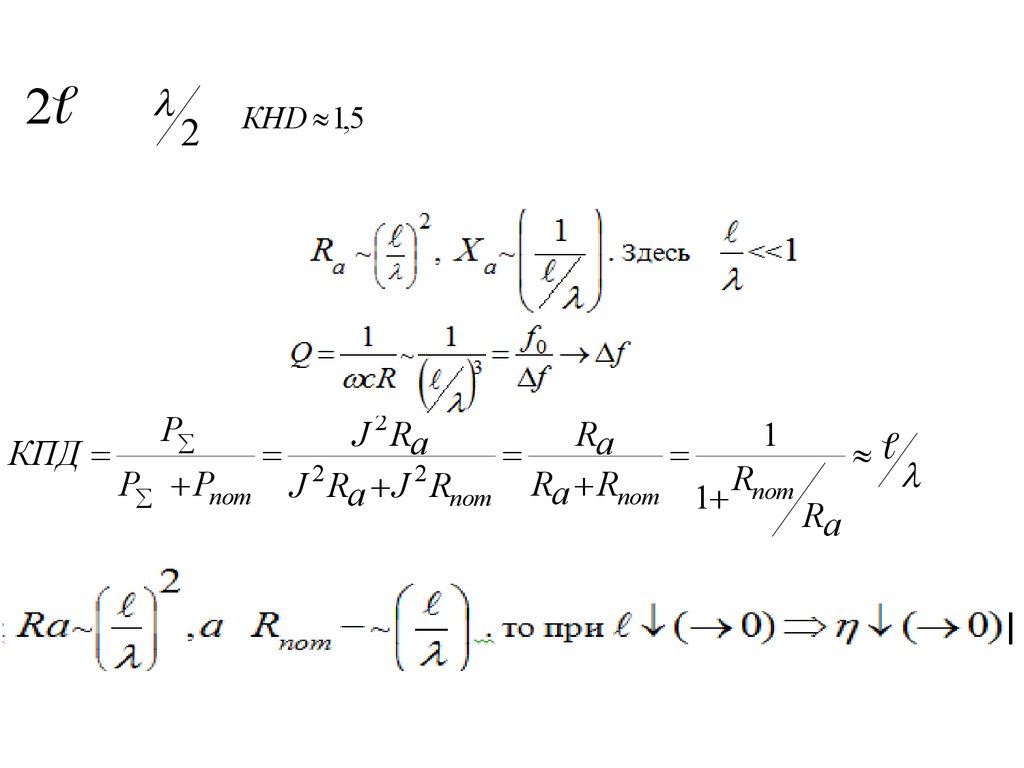
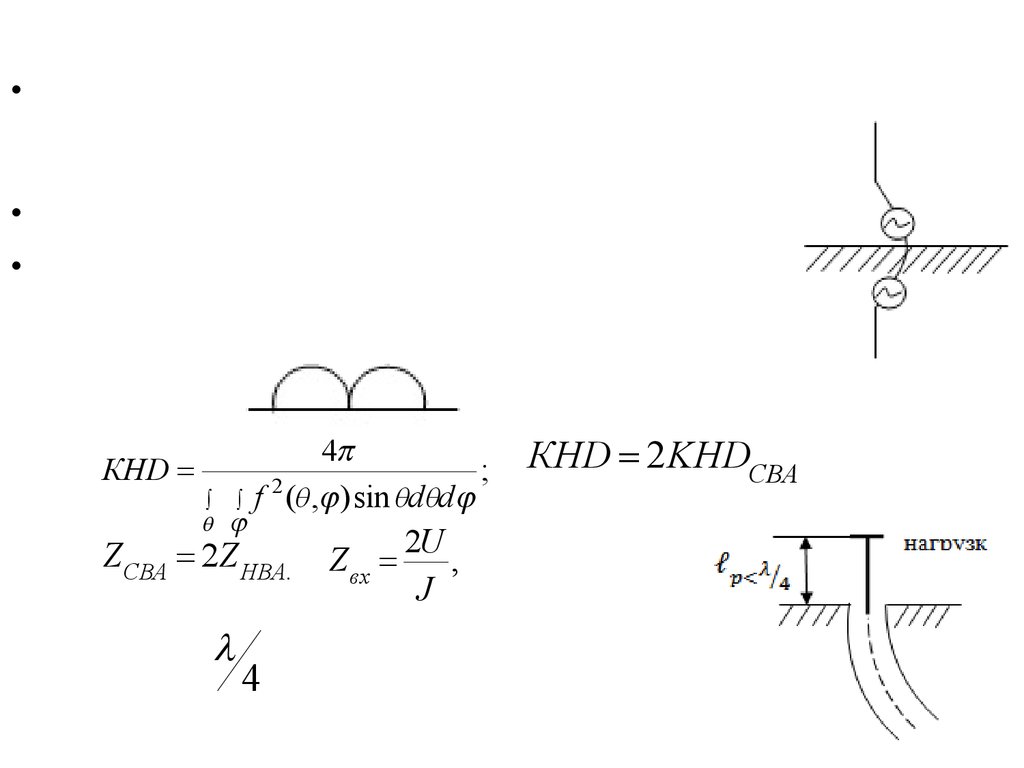
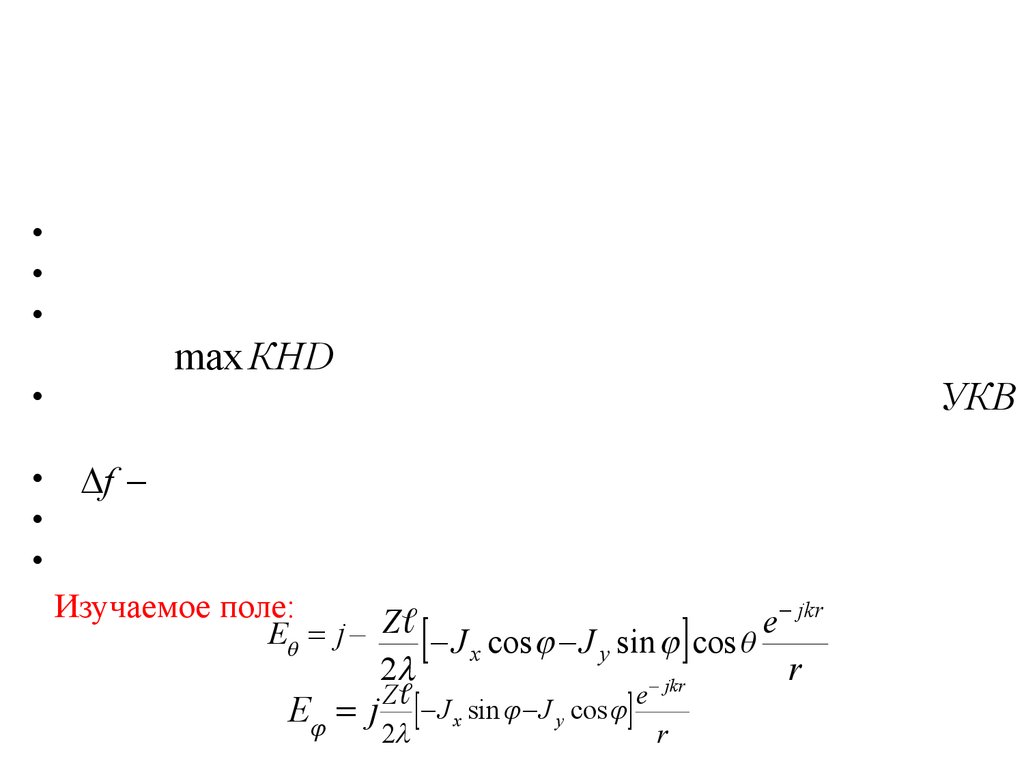
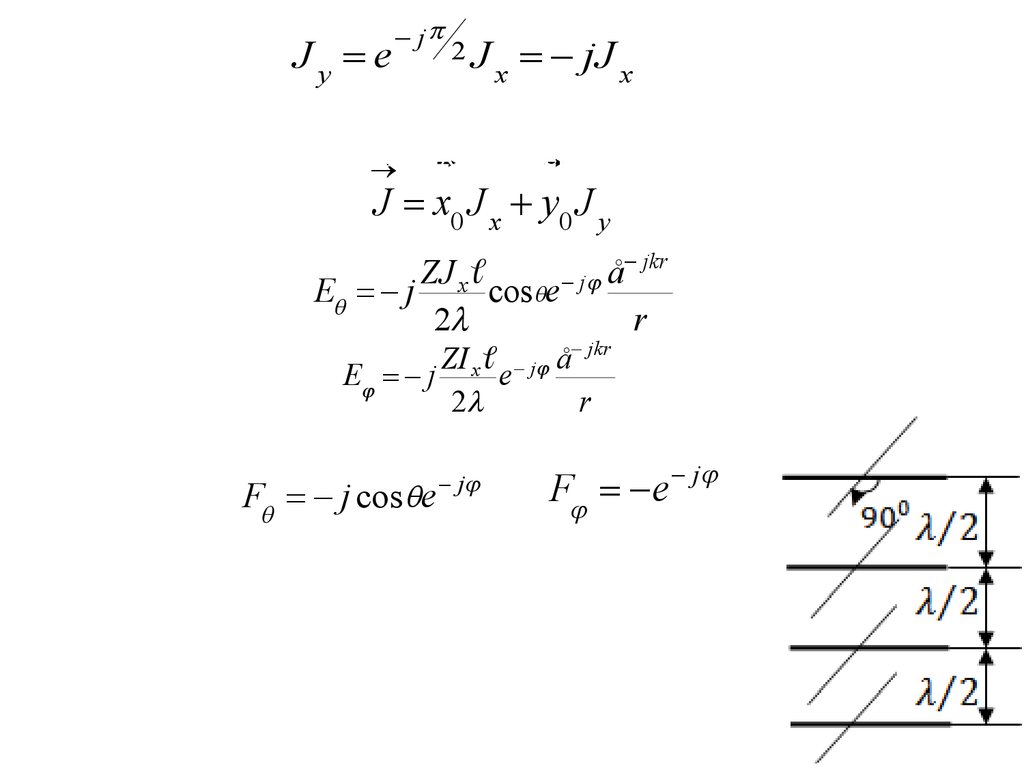
 physics
physics








