Силы и перегрузки действующие на самолет

1.

1

2.

1.5. Силы и перегрузки действующие на самолет
1.5.1. СИЛЫ ПРИ ОТСУТСТВИИ УПРАВЛЯЮЩИХ ВОЗДЕЙСТВИЙ И ВНЕШНИХ ВОЗМУЩЕНИЙ
Движение
самолета
в
происходит под действием:
тяги двигателей
P
и гравитационной силы тяжести
аэродинамической силы планера
полете
G
RA
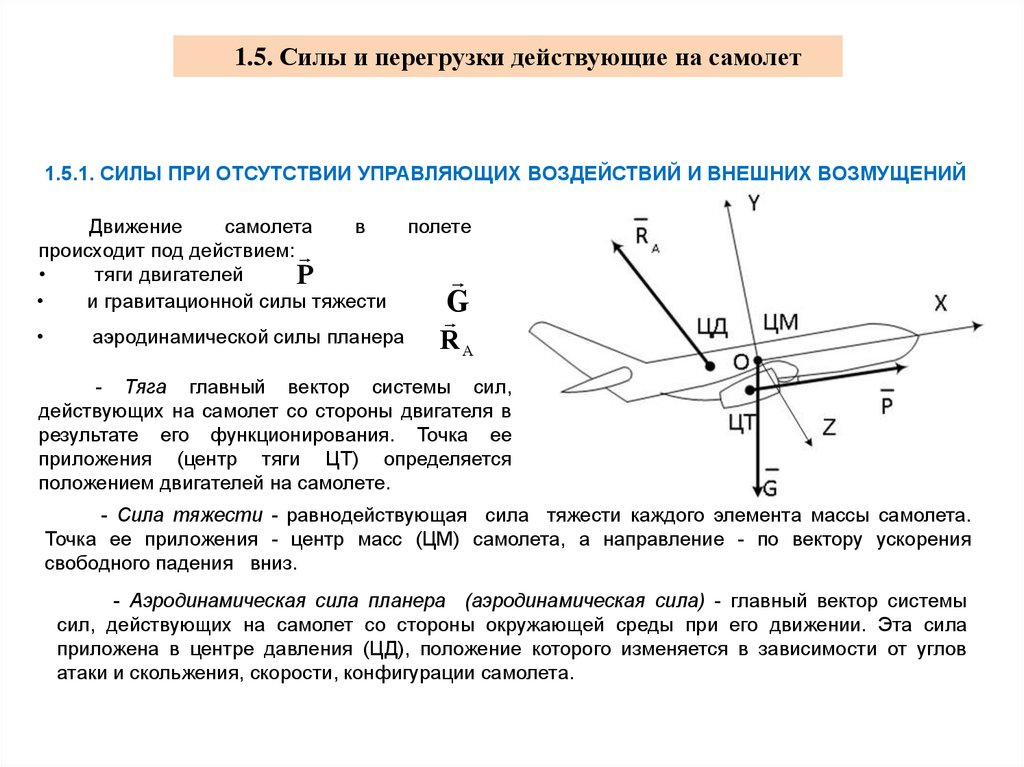
- Тяга главный вектор системы сил,
действующих на самолет со стороны двигателя в
результате его функционирования. Точка ее
приложения (центр тяги ЦТ) определяется
положением двигателей на самолете.
- Сила тяжести - равнодействующая сила тяжести каждого элемента массы самолета.
Точка ее приложения - центр масс (ЦМ) самолета, а направление - по вектору ускорения
свободного падения вниз.
- Аэродинамическая сила планера (аэродинамическая сила) - главный вектор системы
сил, действующих на самолет со стороны окружающей среды при его движении. Эта сила
приложена в центре давления (ЦД), положение которого изменяется в зависимости от углов
атаки и скольжения, скорости, конфигурации самолета.

3.

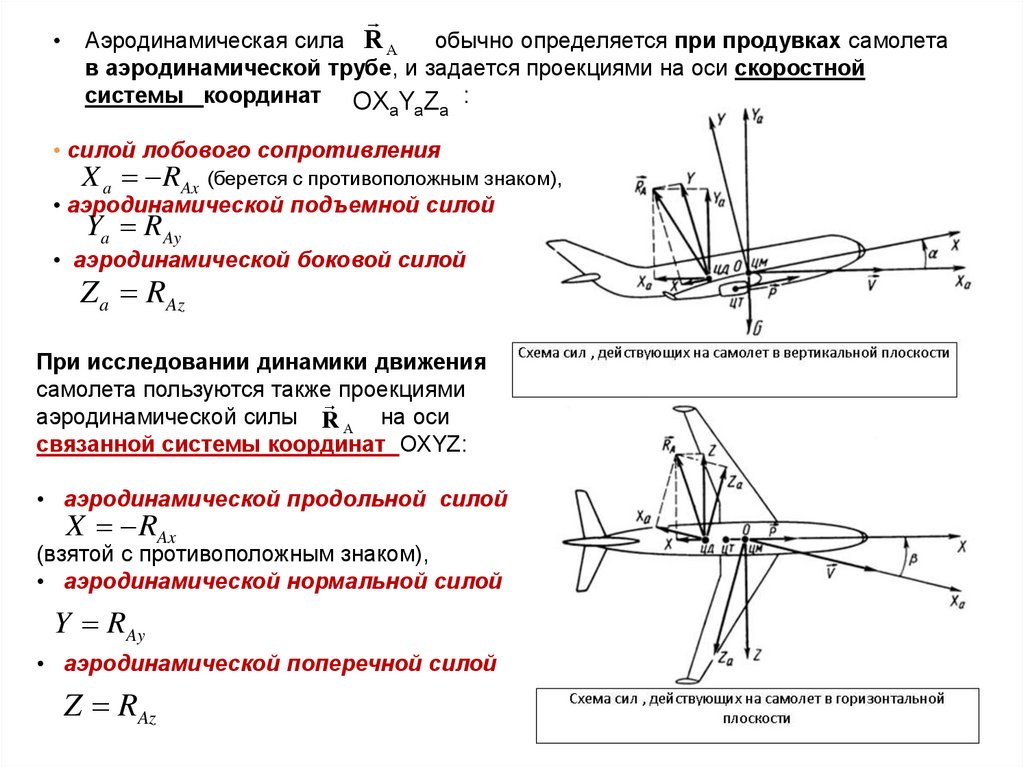
• Аэродинамическая сила R A
обычно определяется при продувках самолета
в аэродинамической трубе, и задается проекциями на оси скоростной
системы координат OX Y Z :
a a a
• силой лобового сопротивления
X a RAx (берется с противоположным знаком),
• аэродинамической подъемной силой
Ya RAy
• аэродинамической боковой силой
Z a RAz
При исследовании динамики движения
самолета пользуются также проекциями
аэродинамической силы R А на оси
связанной системы координат OXYZ:
• аэродинамической продольной силой
X RAx
(взятой с противоположным знаком),
• аэродинамической нормальной силой
Y RAy
• аэродинамической поперечной силой
Z RAz

4.

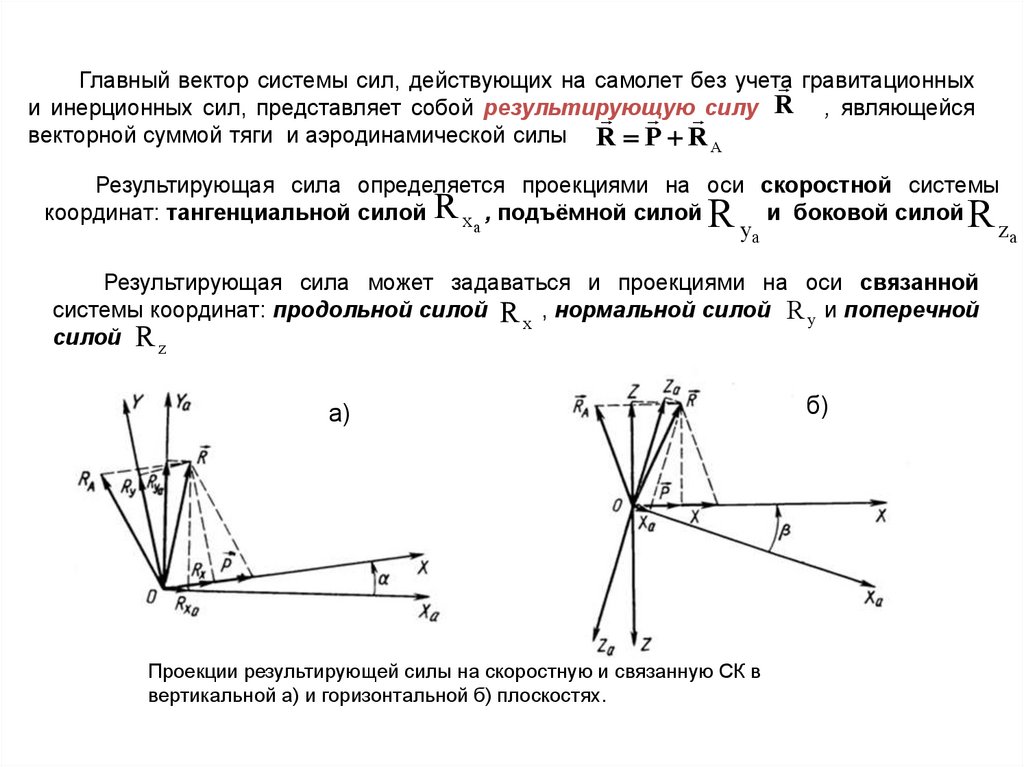
Главный вектор системы сил, действующих на самолет без учета
гравитационных
и инерционных сил, представляет собой результирующую
силу R , являющейся
векторной суммой тяги и аэродинамической силы R P R A
Результирующая сила определяется проекциями на оси скоростной системы
координат: тангенциальной силой R x , подъёмной силой
и боковой силой
a
ya
za
R
R
Результирующая сила может задаваться и проекциями на оси связанной
системы координат: продольной силой R , нормальной силой R y и поперечной
x
силой R z
а)
Проекции результирующей силы на скоростную и связанную СК в
вертикальной а) и горизонтальной б) плоскостях.
б)

5.

Проекции тяги P, аэродинамической силы R А результирующей силы R
обычно выражаются через безразмерные коэффициенты ci , скоростной напор q
и площадь крыла самолета S
.
P cpqS
cp
- коэффициент тяги.
Проекции аэродинамической силы на скоростную систему координат
X a c xa qS,
Ya c ya qS,
c x a , c ya , c z a -
соответственно
коэффициенты
лобового
сопротивления,
аэродинамической подъемной и аэродинамической боковой сил.
Za c za qS,
Проекции аэродинамической силы на связанную систему координат
X c x qS,
Y c y qS,
cx , c y , cz
соответственно
коэффициенты
продольной, нормальной и поперечной сил.
аэродинамических
Z c z qS,
Скоростной напор q
определяется плотностью воздуха
q V 2 / 2
и воздушной скоростью
V

6.

Аэродинамические коэффициенты
аргументов:
Сi
в общем случае являются функциями большого числа
Однако зависимости по отношению ко многим аргументам являются слабыми. Практически при
исследованиях математических моделей самолета всегда используется аппроксимация
коэффициентов функциями относительно небольшого числа переменных, т.к. использование
сложных зависимостей требует больших вычислительных возможностей и огромных объемов
памяти ЭВМ.
Обычно используется аппроксимация аэродинамических коэффициентов суммами и суммами
произведений функций одного-двух, реже, трех аргументов, т.е. в виде полиномов, например:
С Xа Сx 0 ( М ) Сx ( M , а, ) Cx в (а ) в ;
СYа Су 0 (М ) Су (M , а, ) C y в (M , а) В Cy z z C y ;
СZа Сz (M , а, ) Cz в (M , а) В Cz y y Cz ;
Полиномиальная или другая аппроксимация может выполняться не для всей области
допустимого изменения параметров полета сразу, а раздельно для ее подобластей. Тогда
говорят о кусочно- полиномиальной, кусочно-линейной или другой аппроксимации.
При аппроксимации вся информация об аэродинамических характеристиках воплощается в
значения коэффициентов аппроксимирующих функций (например, полиномов) и заданные
области, для которых данная аппроксимация рекомендуется.

7.

1.5.2. Структура составляющих аэродинамических сил
Аэродинамическая подъемная сила
При отсутствии управляющих воздействий и внешних возмущений аэродинамическая
подъемная сила Ya в основном определяется двумя составляющими:
Ya
аэродинамической подъемной силой по углу атаки
Ya Ya YaM
аэродинамической подъемной силой по числу М YaM
(М-отношению скорости полета самолета к скорости звука, М=V/a)
Аэродинамическая подъемная сила по углу атаки возникает вследствие наличия угла
атаки и связанным с этим несимметричным обтеканием самолета воздушным потоком.
Создается в основном крылом, фюзеляжем и горизонтальным оперением.
Аэродинамическая подъемная сила по числу М обусловлена проявлением сжимаемости
воздуха. Создается в основном крылом.
Аэродинамическая подъемная сила может быть определена следующим образом:
Ya ( , M , , V , S ) c ya ( , M ) S
c ya ( , M ) c ya c ya M ,
V 2
2
,

8.

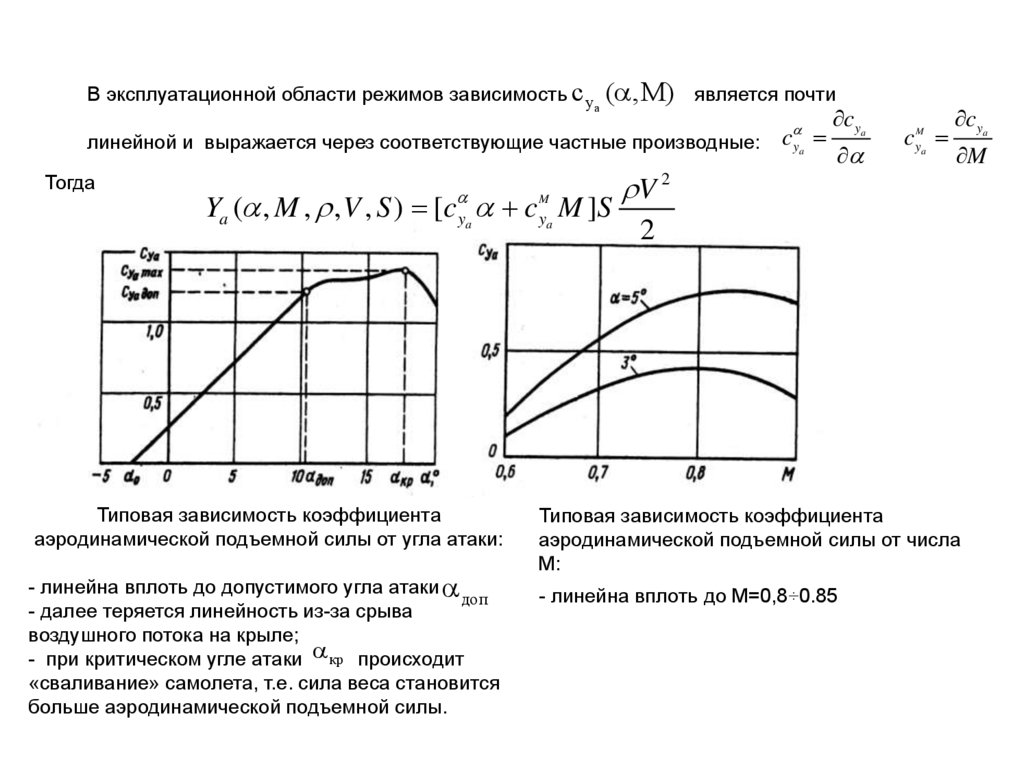
В эксплуатационной области режимов зависимость c y ( , M) является почти
a
линейной и выражается через соответствующие частные производные: c ya
Тогда
Ya ( , M , , V , S ) [c ya c ya M ]S
Типовая зависимость коэффициента
аэродинамической подъемной силы от угла атаки:
- линейна вплоть до допустимого угла атаки
доп
- далее теряется линейность из-за срыва
воздушного потока на крыле;
- при критическом угле атаки кр происходит
«сваливание» самолета, т.е. сила веса становится
больше аэродинамической подъемной силы.
M
V 2
cya
cyMa
cya
M
2
Типовая зависимость коэффициента
аэродинамической подъемной силы от числа
М:
- линейна вплоть до М=0,8÷0.85

9.

Сила лобового сопротивления
Xa
При отсутствии управляющих и возмущающих воздействий сила лобового
сопротивления X a
определяется двумя составляющими :
• силой лобового сопротивления по углу атаки X a
X a X a X a M
• силой лобового сопротивления по числу М X aM
Сила лобового сопротивления по углу атаки обусловлена тем, что при увеличении угла атаки
перераспределяется давление на крыле, меняется эпюра скоростей в пограничном слое, что
приводит к изменению сопротивлений трения и давления.
Сила лобового сопротивления по числу М обусловлена проявлением сжимаемости воздуха. Обе
составляющих силы лобового сопротивления создаются в основном крылом.
Сила лобового сопротивления может быть записана следующим образом:
X a ( , M , , V , S ) cxa ( , M ) S
cxa ( , M ) cxa cxa M ,
V 2
2
,

10.

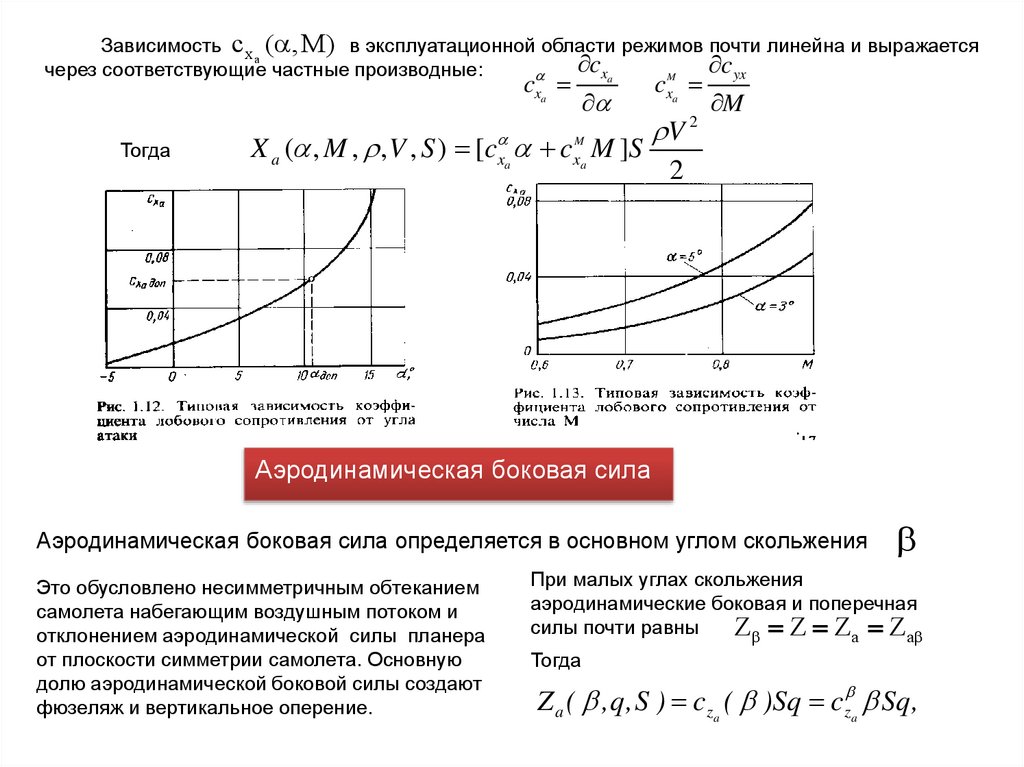
Зависимость c x ( , M) в эксплуатационной области режимов почти линейна и выражается
a
cxa
c yx
через соответствующие частные производные:
M
cxa
Тогда
X a ( , M , , V , S ) [c xa cxMa M ]S
cxa
V
2
M
2
Аэродинамическая боковая сила
Аэродинамическая боковая сила определяется в основном углом скольжения
Это обусловлено несимметричным обтеканием
самолета набегающим воздушным потоком и
отклонением аэродинамической силы планера
от плоскости симметрии самолета. Основную
долю аэродинамической боковой силы создают
фюзеляж и вертикальное оперение.
При малых углах скольжения
аэродинамические боковая и поперечная
силы почти равны
Z Z Za Za
Тогда
Z a ( ,q,S ) cza ( )Sq cz a Sq,

11.

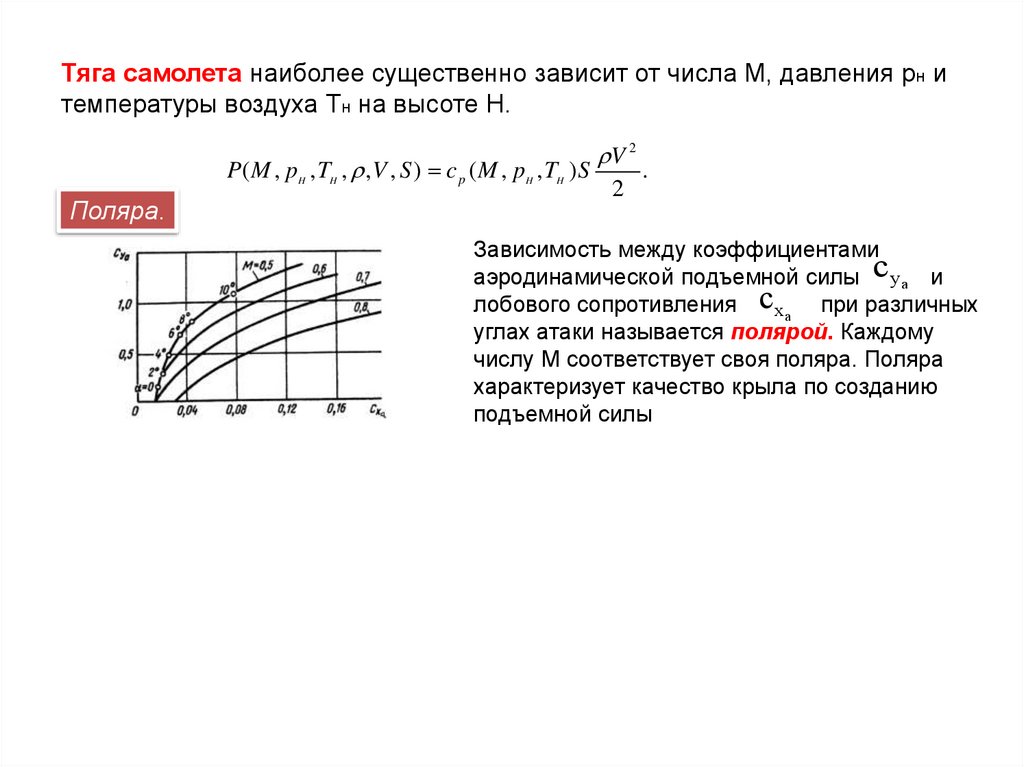
Тяга самолета наиболее существенно зависит от числа М, давления pн и
температуры воздуха Тн на высоте Н.
P( M , pH , TH , , V , S ) c p ( M , pH , TH ) S
Поляра.
V 2
2
.
Зависимость между коэффициентами
аэродинамической подъемной силы c ya и
лобового сопротивления c x a при различных
углах атаки называется полярой. Каждому
числу М соответствует своя поляра. Поляра
характеризует качество крыла по созданию
подъемной силы

12.

1.5.3 Перегрузки, действующие на самолет.
отношение результирующей силы
R
n
Перегрузка
к
произведению массы самолета
свободного падения
на ускорение
R
P RA
n
mg
mg
Проецируя вектор перегрузки на оси связанной СК получим продольную,
нормальную и поперечные перегрузки:
nx
R
Rx
R
, ny y , nz z .
mg
mg
mg
Проецируя вектор перегрузки на оси скоростной СК получим тангенциальную,
нормальную скоростную и боковую перегрузки:
nxa
Ry
Rz
R xa
, n ya a , n za a .
mg
mg
mg
Перегрузка - векторная величина, направленная в сторону противоположную
приложенной силе, вызвавшей изменение скорости, т.е. в сторону противоположную
линейному ускорению.
Для человека очень важно знать направление, величину, длительность и
скорость нарастания возможных перегрузок.

13.

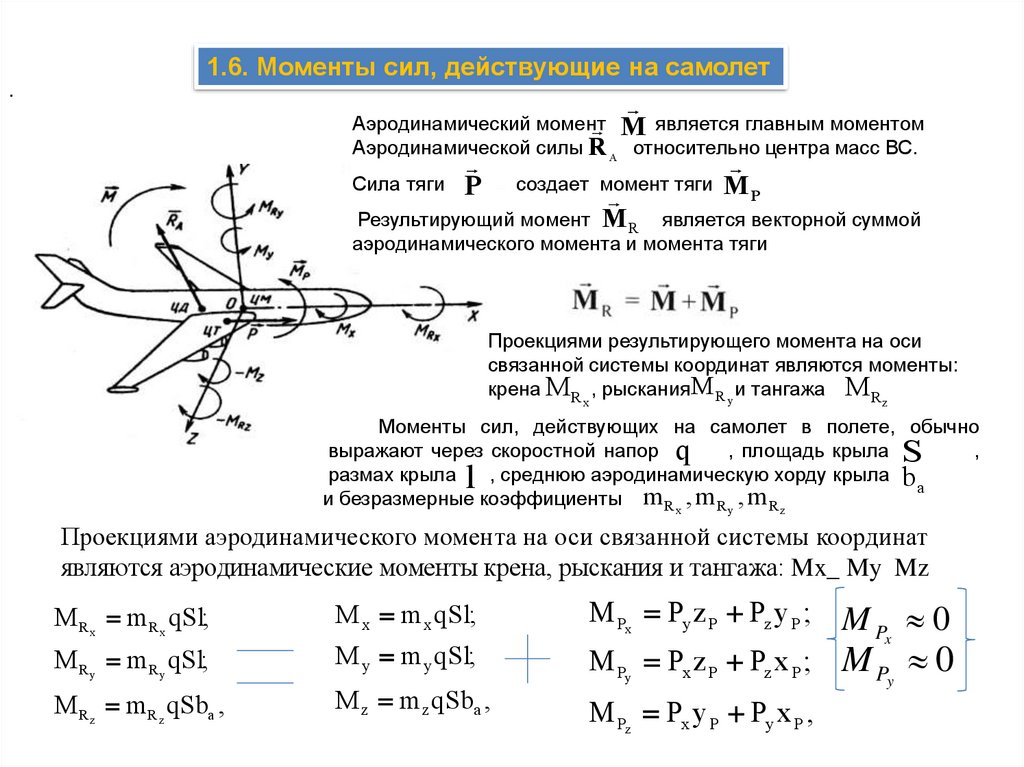
1.6. Моменты сил, действующие на самолет
.
Аэродинамический момент
M является главным моментом
Аэродинамической силы R относительно центра масс ВС.
Сила тяги P
создает момент тяги M
P
Результирующий момент M R является векторной суммой
A
аэродинамического момента и момента тяги
Проекциями результирующего момента на оси
связанной системы координат являются моменты:
крена M R , рысканияM R y и тангажа M R
x
z
Моменты сил, действующих на самолет в полете, обычно
выражают через скоростной напор q
, площадь крыла S
,
размах крыла
, среднюю аэродинамическую хорду крыла b
a
и безразмерные коэффициенты m R x , m R y , m R z
l
Проекциями аэродинамического момента на оси связанной системы координат
являются аэродинамические моменты крена, рыскания и тангажа: Mx_ My Mz
M x m x qSl;
M Px Py z P Pz y P ;
M R y m R y qSl;
M y m y qSl;
M R z m R z qSba ,
M z m z qSba ,
M Py Px z P Pz x P ;
M R x m R x qSl;
M Pz Px y P Py x P ,
M Px 0
M Py 0

14.

1.6. СТРУКТУРА МОМЕНТОВ СИЛ
За положительное направление действия моментов принимается их действие,
происходящее по направлению часовой стрелки, если смотреть по соответствующей оси
от центра масс самолета.
Аэродинамический момент крена
Mx =Mxβ +Mxα +Mxωx +Mxωy
M x
- Статический момент крена по углу скольжения. Связан с несимметричным обтеканием
M x
- Статический момент крена по углу атаки. Связан с несимметричным обтеканием
самолета воздушным потоком при вертикальном маневре. В горизонтальном полете
меньше , чем M x
M x x
- Динамический демпфирующий момент крена. Связан с увеличением угла атаки на
опускающемся крыле и уменьшением угла атаки на поднимающемся крыле. Создается
в основном крылом, а также вертикальным и горизонтальным оперением. Направлен
против угловой скорости вращения самолета и против статического момента M x .
Пропорционален угловой скорости вращения
самолета воздушным потоком. Создается в основном крылом и вертикальным
оперением. Направлен в сторону отстающего при скольжении полукрыла.
x
M x y
- Динамический спиральный момент крена. Создается в основном крылом и
вертикальным оперением. На идущем вперед полукрыле подъемная сила увеличивается
и оно поднимается, а на идущем назад полукрыле - уменьшается и оно опускается.
Пропорционален угловой скорости вращения y
.

15.

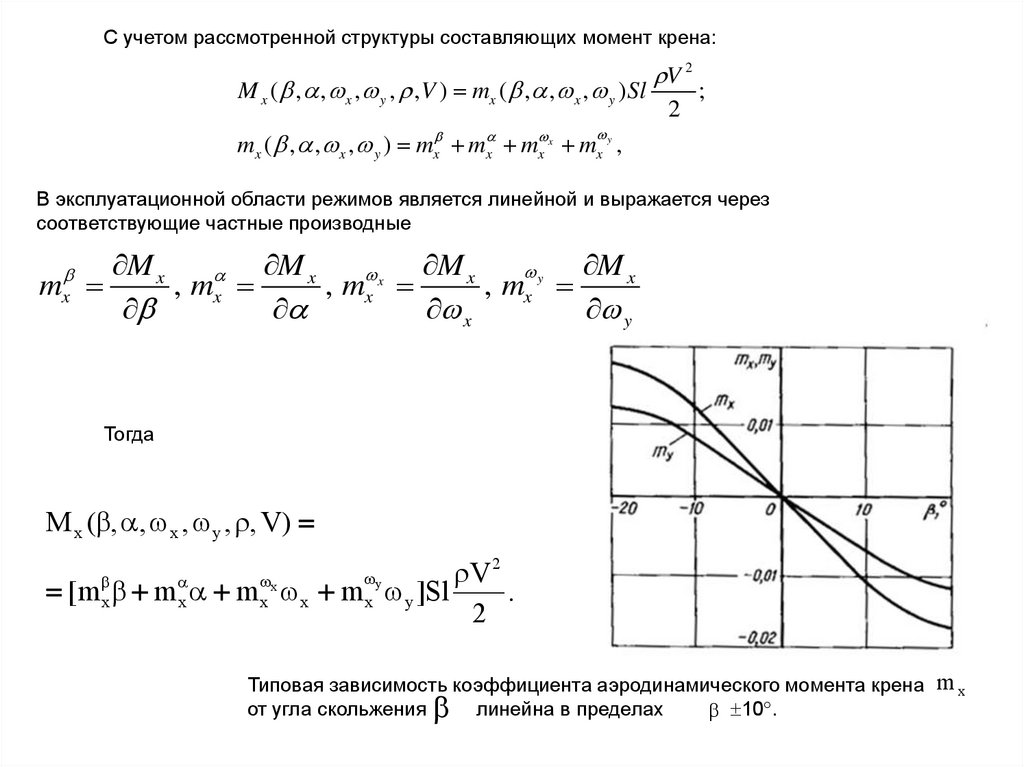
С учетом рассмотренной структуры составляющих момент крена:
M x ( , , x , y , , V ) mx ( , , x , y ) Sl
V 2
2
;
mx ( , , x , y ) mx m x mx x mx y ,
В эксплуатационной области режимов является линейной и выражается через
соответствующие частные производные
M x
M x
M x
M x
, m x
, m x x
, mx y
x
y
mx
Тогда
M x ( , , x , y , , V)
V 2
[m m m x m y ]Sl
.
2
x
x
x
x
y
x
Типовая зависимость коэффициента аэродинамического момента крена m x
от угла скольжения линейна в пределах
10 .

16.

Аэродинамический момент рыскания
M y M y M y M y y M y x
M y
M y
M y y
M y x
- Статический момент рыскания по скольжению. Образуется вследствие появления
аэродинамической поперечной силы при скольжении. Является основным статическим
моментом.
- Статический момент рыскания по углу атаки. Возникает при наличии угла атаки и
связанного с этим несимметричным обтеканием самолета воздушным потоком при
вертикальном маневре самолета. Значительно меньше статического момента по
скольжению
- Динамический демпфирующий момент рыскания. Возникает вследствие вращения
самолета с угловой скоростью y . Пропорционален угловой скорости и направлен
против угловой скорости y
-Динамический спиральный момент рыскания. Образуется при вращении самолета
вокруг оси ОХ с угловой скоростью x . Возникающие скорости концов плоскостей
приводят к увеличению лобового сопротивления на опускающемся крыле и
уменьшению лобового сопротивления на поднимающемся крыле. Это приводит к
появлению момента относительно оси ОУ . Пропорционален величине угловой
скорости
x

17.

С учетом рассмотренной структуры составляющих момент рыскания равен:
M y ( , , x , y , , V ) m y ( , , x , y ) Sl
m y ( , , x , y ) my m y m y x my y ,
V 2
2
,
где
m y , m y , m y x , m y yсоставляющие коэффициента аэродинамического момента рыскания m y
В эксплуатационной области режимов зависимость m y ( , , y , x )
линейна и выражается через соответствующие частные производные
my
M y
, my
M y
y
, my
M y
y
x
, my
M y
x
. Тогда
M y ( , , x , y , , V)
V 2
[m m m y m x ]Sl
.
2
y
y
y
y
x
y
Типовая зависимость коэффициента аэродинамического момента рыскания m y от угла
скольжения линейна в пределах = 15 .

18.

Аэродинамический момент тангажа
M z M zo M z M z M z z M z
M zo
-Статический момент тангажа при нулевой подъемной силе. Создается силой лобового
сопротивления относительно точки приложения подъемной силы. Этот момент не зависит от
угла атаки.
M z
-Статический момент тангажа по углу атаки. Обусловлен углом атаки и связанной с этим
подъемной силой. Он создается в основном крылом. В прямолинейном полете момент M z основной действующий момент относительно оси ОZ .
M z
-Статический момент тангажа по углу скольжения. Обусловлен углом скольжения и связанного с
этим несимметричного обтекания самолета воздушным потоком при горизонтальном маневре
самолета. По величине значительно меньше момента M z
M z z
-Динамический демпфирующий момент тангажа. Возникает вследствие вращения самолета
вокруг оси ОZ. Он создается в основном горизонтальным оперением, а также крылом и
фюзеляжем. По величине пропорционален, по направлению противоположен направлению
угловой скорости тангажа
M z
Динамический демпфирующий момент скоса воздушного потока. Возникает вследствие
изменения скорости угла атаки. Он создается в основном горизонтальным оперением. По
величине пропорционален угловой скорости угла атаки, по направлению совпадает с
моментом демпфирования

19.

1.7. УПРАВЛЯЮЩИЕ ВОЗДЕЙСТВИЯ.
Существуют два основных способа аэродинамического управления движением
самолета.
1.
Первый предусматривает управление аэродинамическими моментами путем
отклонения пилотом или автоматикой моментных органов управления: элеронов, рулей
направления и высоты.
2.
Второй способ предусматривает управление аэродинамическими силами путем
отклонения пилотом или автоматикой органов управления силами: тормозных щитков,
интерцепторов, закрылков, подфюзеляжного руля совместно с рулем направления и т. д.
В первом способе
1. Управляющее воздействие по крену угол отклонения элеронов δЭ для создания
управляющего аэродинамического момента крена.
Если штурвал против часовой стрелки, то
правый элерон вниз, (означает + δЭ ) при этом
возникают:
управляющий аэродинамический момент крена
Mxδэ =2ΔYэ zэ =Mδxэ δэ =mδxэ qSlδэ
mхδэ-коэффициент эффективности элеронов по крену.
аэродинамический момент рыскания
Myδэ =2ΔXэ zэ =Mδyэ δэ =mδyэ qSlδэ
mуδэ коэффициент эффективности элеронов
по рысканию

20.

2.Управляющее воздействие по рысканию - угол отклонения руля направления δН для
создания аэродинамического момента рыскания.
Необходимо правую педаль отклонить от себя, а левую - на себя. Тогда руль направления пойдет
вправо (положительное отклонение). Возникает поперечная сила ZH , на плече LH появляется
-управляющий аэродинамический момент рыскания
δн
y
δн
y
Myδн =Zн Lн =M δн =m qSlδн
mуδн - коэффициент
направления по рысканию.
эффективности руля
-аэродинамический момент крена, создаваемый поперечной силой ZH на плече Yн:
Myδн =Zн yн =Mδyн δн =mδyн qSlδн
Зависимость коэффициента
аэродинамического момента крена от
отклонения элеронов
Зависимость коэффициента
аэродинамического момента рыскания от
отклонения рулей направления

21.

3. Управляющее воздействие по тангажу
угол отклонения рулей высоты δВ для создания
управляющего аэродинамического момента
тангажа
4. Управляющее балансировочное воздействие
по тангажу угол отклонения стабилизатора φ для
создания аэродинамического балансировочного
момента тангажа.
При отклонении колонки штурвала от себя,
рули высоты пойдут вниз (положительное
отклонение), возникает ΔYв на хвостовом
оперении, возникает
управляющий момент тангажа
Положителен, если задняя кромка стабилизатора
отклоняется вниз, для чего необходимо отжать
гашетку управления стабилизатором от себя,
возникает ΔYс на хвостовом оперении, возникает
управляющий балансировочный момент
тангажа
Mzδв = Yв Lго =Mδzв δв =mδzв qSbа δв
mzδв - коэффициент эффективности
рулей высоты по тангажу.
Зависимость коэффициента
аэродинамического момента тангажа
от отклонения рулей высоты.
.
Mzφ = Yс L с =Mφz φ=mφz qSbа φ
mzφ
-коэффициент
стабилизатора по тангажу.
эффективности

22.

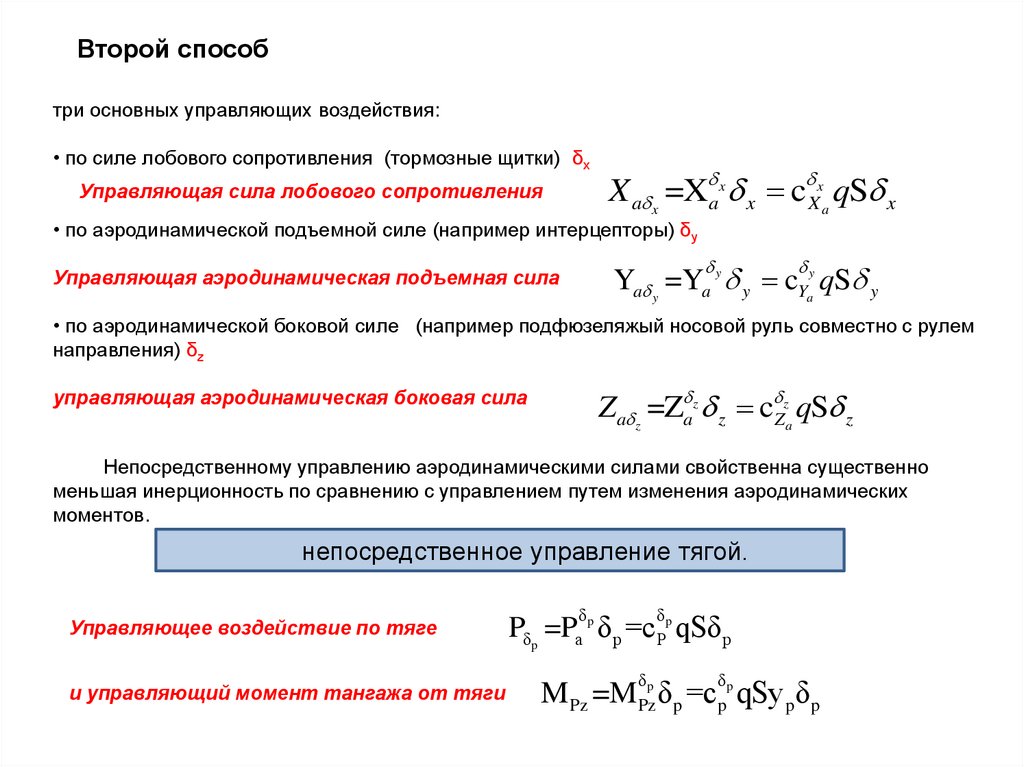
Второй способ
три основных управляющих воздействия:
• по силе лобового сопротивления (тормозные щитки) δx
Управляющая сила лобового сопротивления
X a x =X ax x c Xxa qS x
• по аэродинамической подъемной силе (например интерцепторы) δу
Ya y =Ya y y cYay qS y
Управляющая аэродинамическая подъемная сила
• по аэродинамической боковой силе (например подфюзеляжый носовой руль совместно с рулем
направления) δz
Za z =Z az z c Zza qS z
управляющая аэродинамическая боковая сила
Непосредственному управлению аэродинамическими силами свойственна существенно
меньшая инерционность по сравнению с управлением путем изменения аэродинамических
моментов.
непосредственное управление тягой.
Управляющее воздействие по тяге
и управляющий момент тангажа от тяги
δ
δ
Pδp =Pa p δ p =c Pp qSδ p
δ
δ
M Pz =M Pzp δp =cpp qSyp δp

23.

1.8. ВНЕШНИЕ ВОЗМУЩЕНИЯ.
,
,
Условно делятся на две группы:
связанные с изменением состояния самолета: выпуском механизации крыла и
шасси, отказом двигателя и т. д.
связанные с изменением состояния окружающей среды: ветром, турбулентностью
атмосферы и т. д.
Действие первой группы приводят к удобному для исследований виду - внешним
силам и моментам :
Результирующая внешняя сила FB - главный вектор системы внешних сил,
действующих на самолет вследствие изменения его состояния. Определяется проекциями на
оси связанной системы координат:
внешней продольной силой fx,
внешней нормальной силой fу
внешней поперечной силой fz.
FB изменяет силу лобового сопротивления, аэродинамические подъемную и боковую силы

24.

Результирующий внешний момент Мв- главный вектор системы внешних моментов,
действующих на самолет вследствие изменения его состояния. Он определяется проекциями на
оси связанной системы координат:
внешним моментом крена mхв,
внешним моментом рыскания mув
внешним моментом тангажа mzb.
Внешний момент Мв изменяет аэродинамические моменты крена, рыскания и тангажа
следующим образом:
С учетом управляющих воздействий и внешних возмущений аэродинамические силы,
действующие на самолет, имеют вид:
С учетом управляющих воздействий и внешних возмущений аэродинамические
моменты, действующие на самолет, определяют следующим образом:

25.

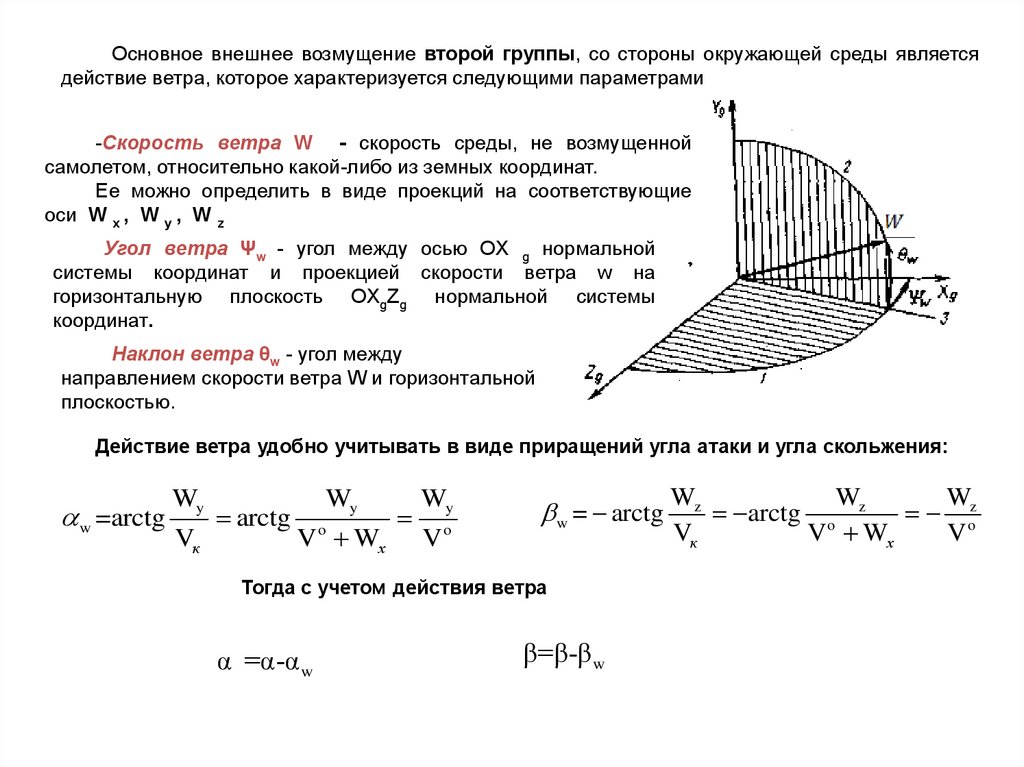
Основное внешнее возмущение второй группы, со стороны окружающей среды является
действие ветра, которое характеризуется следующими параметрами
-Скорость ветра W - скорость среды, не возмущенной
самолетом, относительно какой-либо из земных координат.
Ее можно определить в виде проекций на соответствующие
оси W x , W y , W z
Угол ветра Ψw - угол между осью OX g нормальной
системы координат и проекцией скорости ветра w на
горизонтальную плоскость OXgZg нормальной системы
координат.
Наклон ветра θw - угол между
направлением скорости ветра W и горизонтальной
плоскостью.
Действие ветра удобно учитывать в виде приращений угла атаки и угла скольжения:
w =arctg
Wy
Vк
arctg
Wy
V o Wx
Wy
Vo
w = arctg
Тогда с учетом действия ветра
α =α-α w
β=β-β w
Wz
W
W
arctg o z
oz
Vк
V Wx
V

26.

Тема 1.2. Математические модели пространственного движения самолёта
Лекция 2. Математические модели пространственного движения самолёта.
Общее представление о моделях движения ВС, их характеристика.
Пространственное движение самолета описывается системой дифференциальных
уравнений. При этом данная система включает дифференциальные уравнения,
описывающие движение центра масс самолета (поступательное движение),
движение самолета вокруг центра масс(вращательное движение) и кинематические
соотношения между параметрами самолета:
-уравнения поступательного движения (3).
- уравнения вращательного движения (3).
- кинематические соотношения между
параметрами.
Классификация движений ВС по различным признакам представлен на следующем
плакате
26

27.

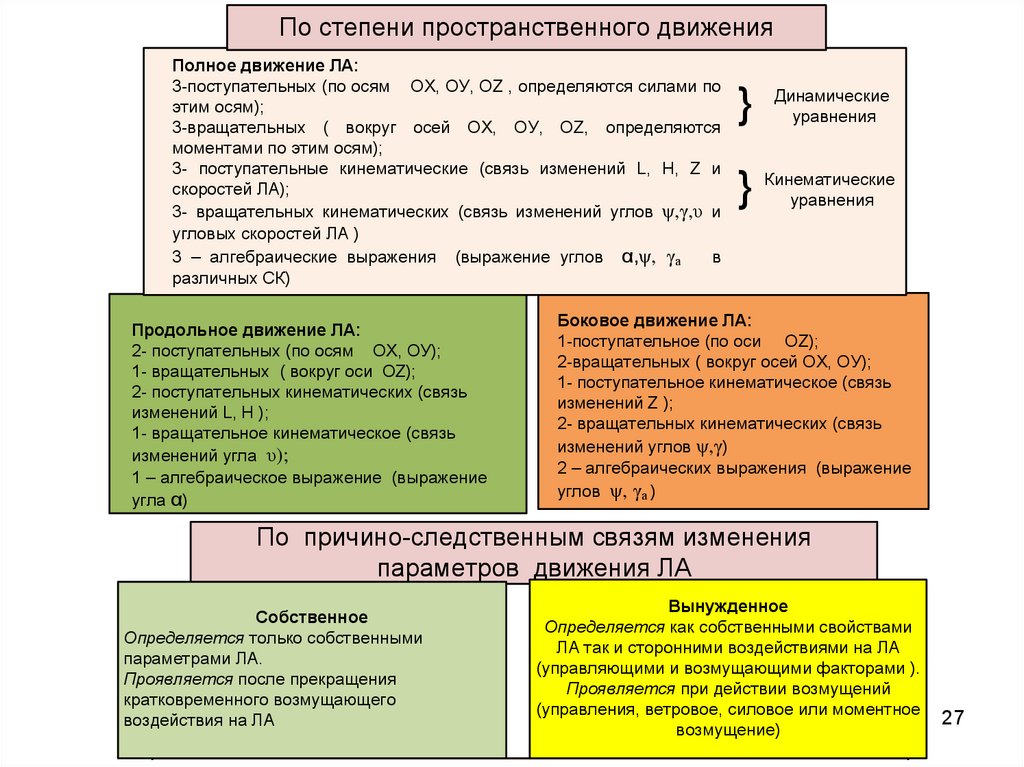
По степени пространственного движения
Полное движение ЛА:
3-поступательных (по осям ОХ, ОУ, ОZ , определяются силами по
этим осям);
3-вращательных ( вокруг осей ОХ, ОУ, ОZ, определяются
моментами по этим осям);
3- поступательные кинематические (связь изменений L, H, Z и
скоростей ЛА);
3- вращательных кинематических (связь изменений углов ψ,γ,υ и
угловых скоростей ЛА )
3 – алгебраические выражения (выражение углов α,ψ, γа
в
различных СК)
Продольное движение ЛА:
2- поступательных (по осям ОХ, ОУ);
1- вращательных ( вокруг оси ОZ);
2- поступательных кинематических (связь
изменений L, H );
1- вращательное кинематическое (связь
изменений угла υ);
1 – алгебраическое выражение (выражение
угла α)
} Динамические
уравнения
} Кинематические
уравнения
Боковое движение ЛА:
1-поступательное (по оси ОZ);
2-вращательных ( вокруг осей ОХ, ОУ);
1- поступательное кинематическое (связь
изменений Z );
2- вращательных кинематических (связь
изменений углов ψ,γ)
2 – алгебраических выражения (выражение
углов ψ, γа )
По причино-следственным связям изменения
параметров движения ЛА
Собственное
Определяется только собственными
параметрами ЛА.
Проявляется после прекращения
кратковременного возмущающего
воздействия на ЛА
Вынужденное
Определяется как собственными свойствами
ЛА так и сторонними воздействиями на ЛА
(управляющими и возмущающими факторами ).
Проявляется при действии возмущений
(управления, ветровое, силовое или моментное
возмущение)
27

28.

2.1.1 Уравнения собственного поступательного движения.
Собственное поступательное движение самолета описывается системой
динамических и кинематических дифференциальных уравнений.
Динамические уравнения описывают движение центра масс самолета относительно
Земли и позволяют установить зависимость между параметрами поступательного
движения самолета относительно Земли (земной скоростью, углом пути, углом
наклона траектории) и параметрами движения самолета относительно
воздушного потока (углом атаки, углом скольжения и скоростным углом крена)
Динамические уравнения поступательного движения получаются на основе теоремы
об изменении количества движения системы, «производная по времени от
количества движения системы равна геометрической сумме всех действующих
на систему внешних сил». (Количество движения –