Similar presentations:
Прямая линия. Лекция 2
1.
КАФЕДРА ИНЖЕНЕРНОГО ПРОЕКТИРОВАНИЯНАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
2.
ДОЦЕНТПОНОМАРЕНКО ЕВГЕНИЙ АНАТОЛЬЕВИЧ
2
3.
ЛЕКЦИЯ 2ПРЯМАЯ ЛИНИЯ
3
4.
Прямые бывают общего и частного положенияСвойства прямой:
1. Проекция прямой на плоскость – всегда
прямая.
2. В общем случае – прямая безгранична. Для
ограничения положения достаточно две (•) точки,
принадлежащей прямой.
Если эти (•)(•) спроецировать проекции на
плоскости координат, то получим проекции
отрезка прямой.
3. Для определения положения прямой в
пространстве достаточно две проекции.
4
5.
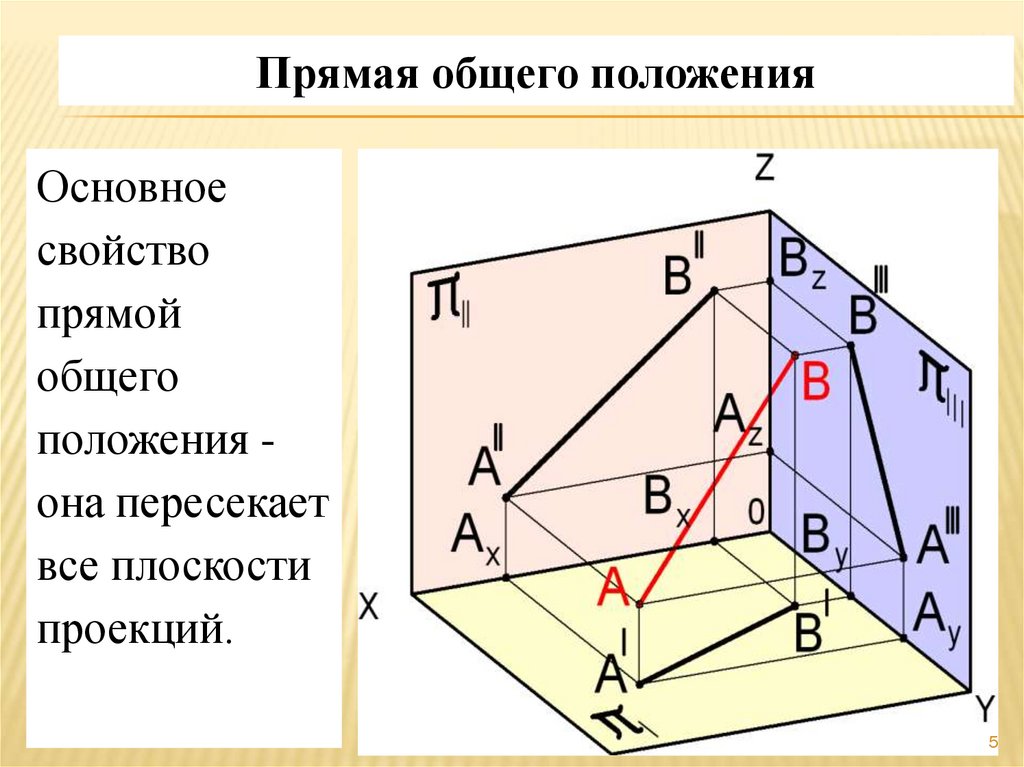
Прямая общего положенияОсновное
свойство
прямой
общего
положения она пересекает
все плоскости
проекций.
5
6.
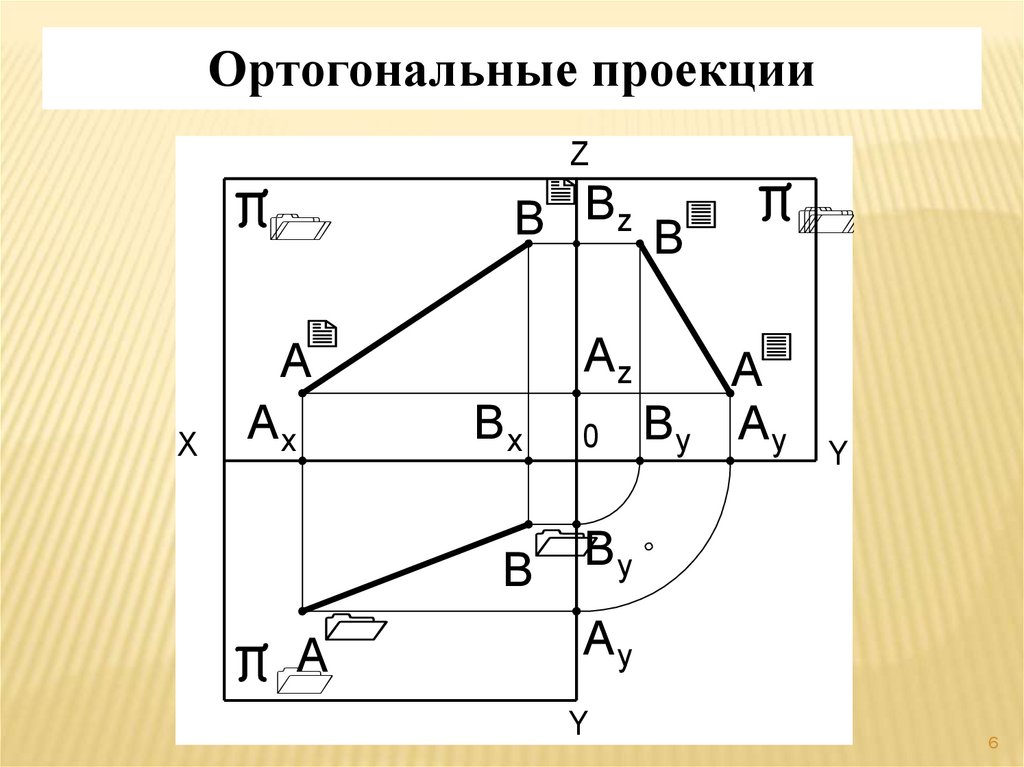
Ортогональные проекцииZ
В
B
Ах
Вх
В
А
B
Вy
0
В
Аz
А
Х
z
A
Аy
Y
y
Аy
Y
6
7.
Размеры проекций линии общего положенияне равны истинной длине.
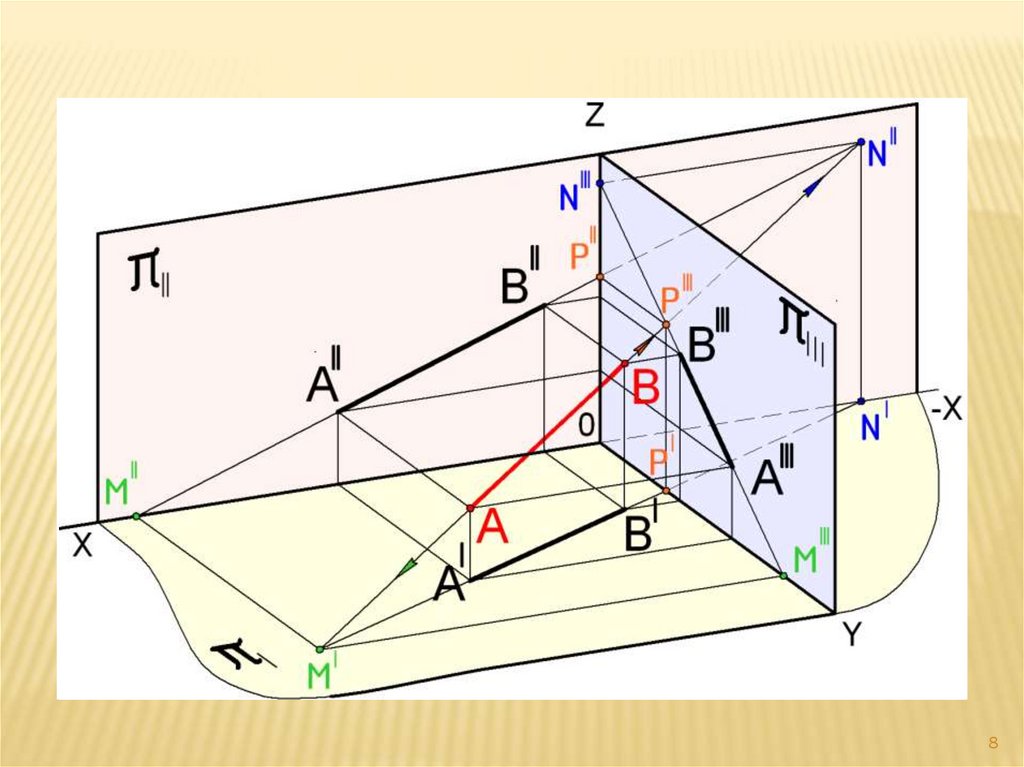
Следы прямой линии
Точку пересечения (встречи) прямой с
плоскостью проекции называют следом
прямой на данной плоскости.
Прямая общего положения имеет три следа:
M-горизонтальный след прямой на плоскости;
N- фронтальный след прямой на плоскости;
P- профильный след прямой на плоскости.
7
8.
89.
Прямые частного положения.Прямые могут быть параллельны плоскости
проекций, принадлежат плоскости проекций и
могут, находятся на оси координат.
1. Прямые параллельные плоскостям координат.
Прямые, параллельные какой-либо плоскости
проекции, называют линиями уровнями.
9
10.
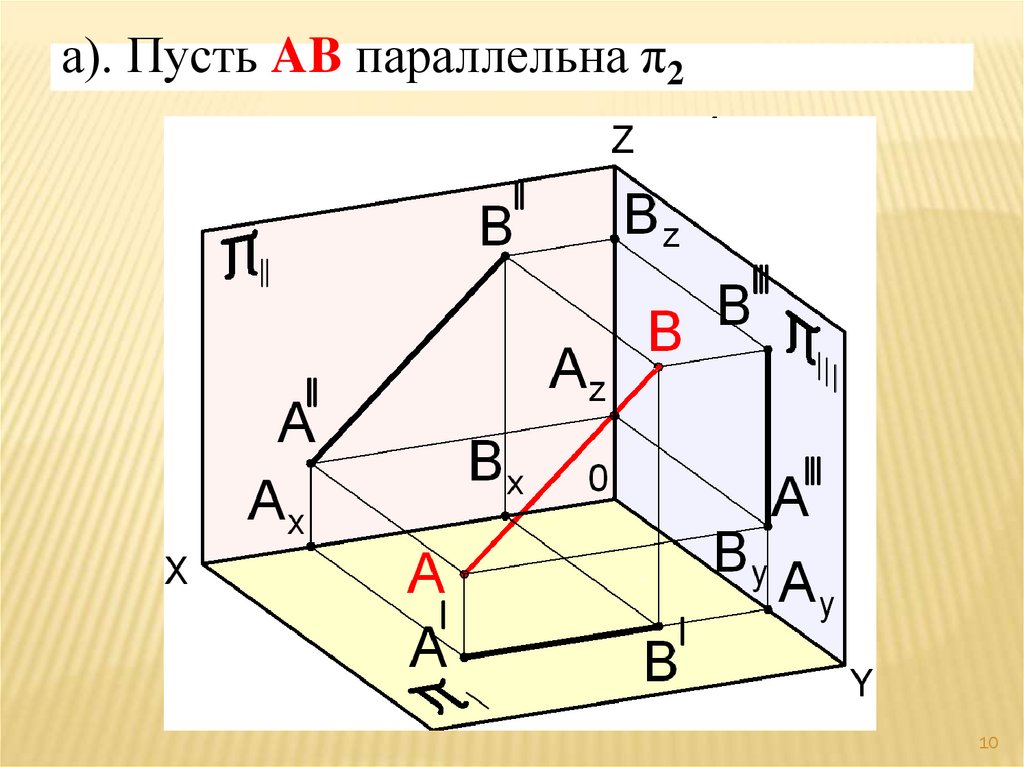
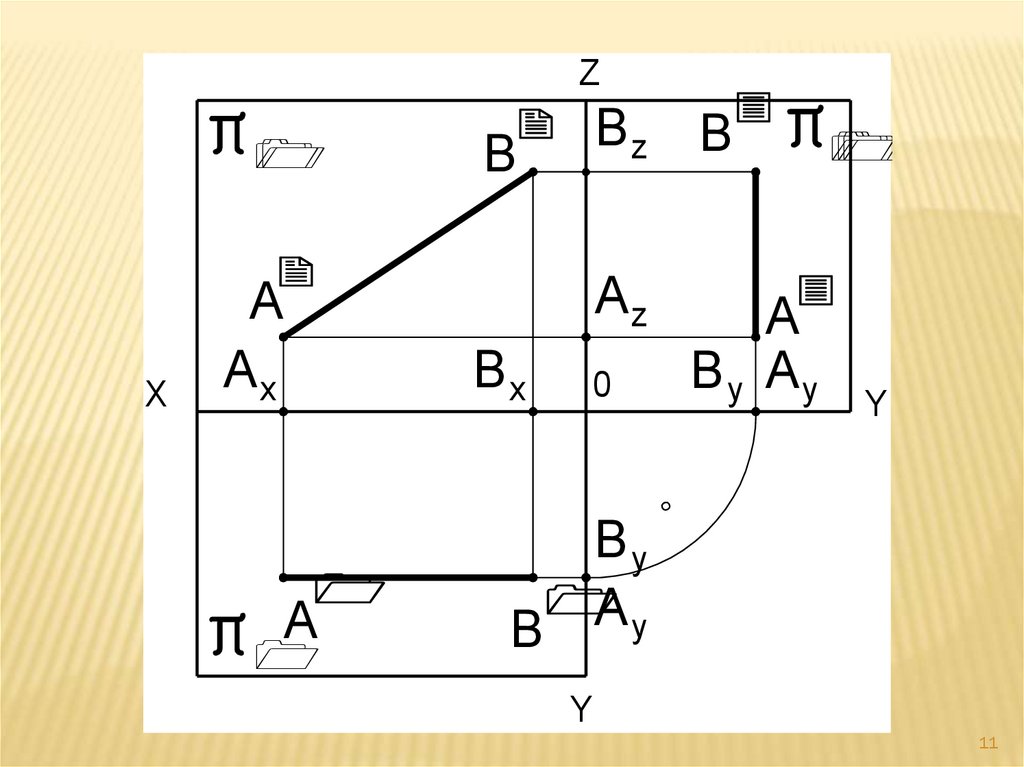
а). Пусть AB параллельна π210
11.
ZB
Х
А
Ах
Аz
Вх
А
Вz B
0
A
Вy Аy
Y
Вy
А
y
В
Y
11
12.
Прямая AB - фронталь.Основное свойство фронтали.
Горизонтальная проекция фронтали
(ГПФ)
А ׀В ׀параллельна оси OX, а фронтальная
проекция фронтали (ФПС) А ׀׀В׀׀
истинная величина (длина) прямой AB.
12
13.
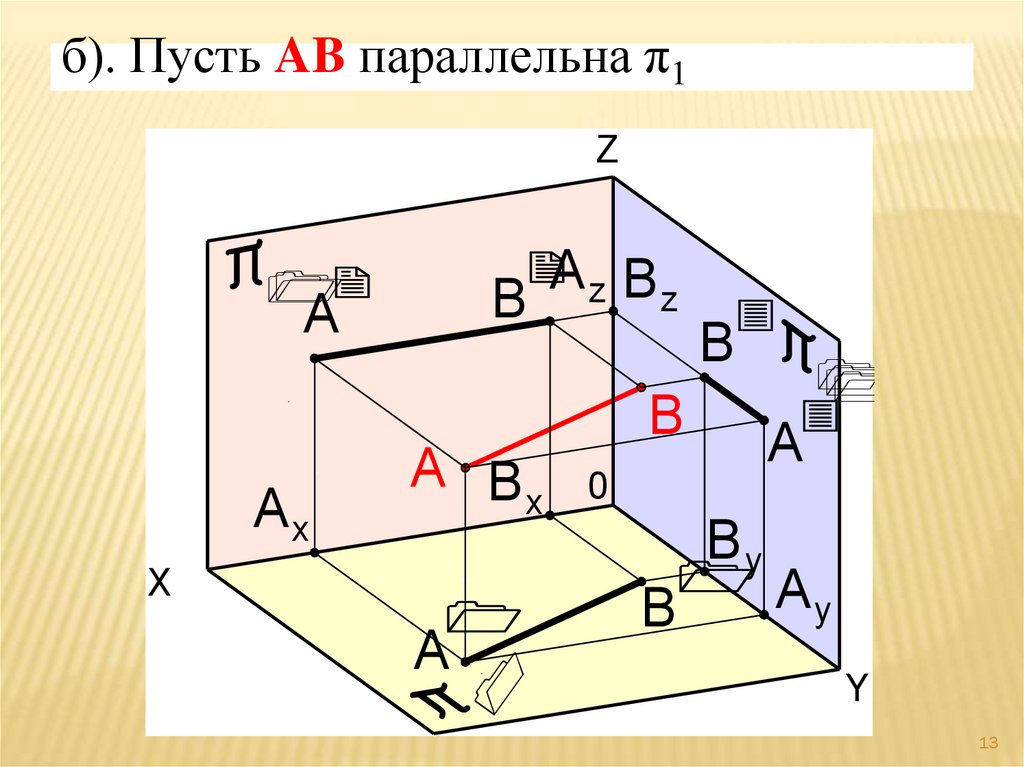
б). Пусть AB параллельна π1Z
А z
B
А
Х
А
Ах
А Вх
Вz
B
В
A
0
Вy
В
Аy
Y
13
14.
ZА
Х
Ах
А
B
B
Вz Аz
Вх
Вy
0
В
В
A
Аy
Y
y
Аy
Y
14
15.
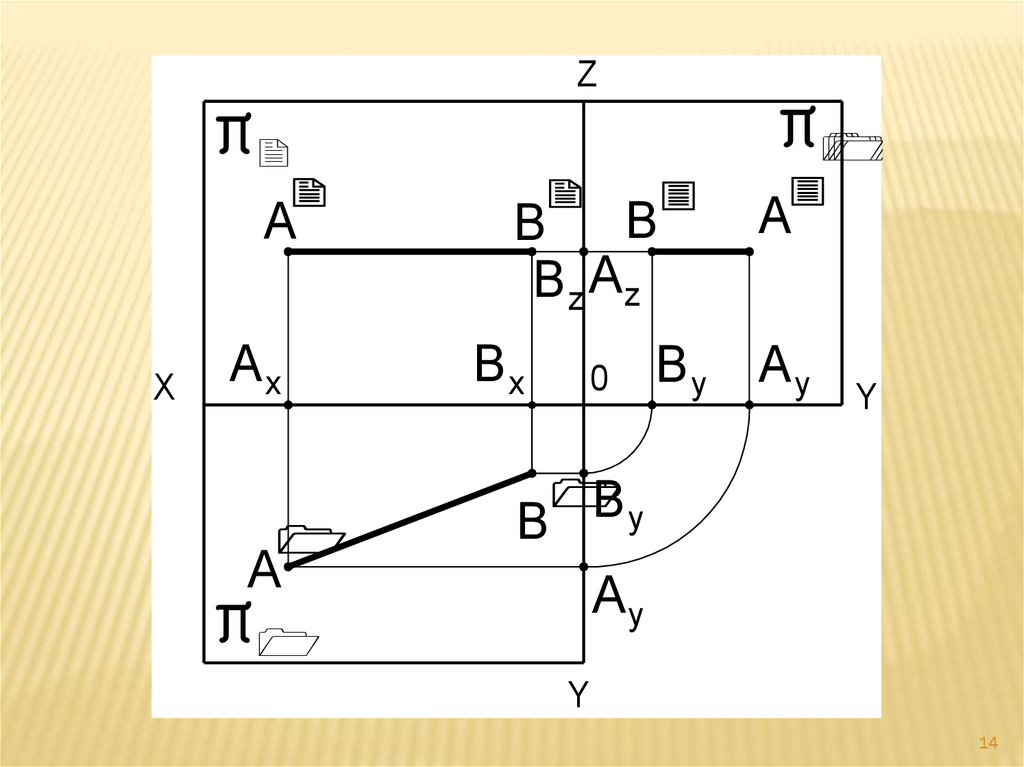
Прямая AB - горизонталь.Основное свойство горизонтали.
Фронтальная проекция горизонтали
(ФПГ)
А ׀׀В ׀׀параллельна оси OX, а
горизонтальная проекция горизонтали
(ГПГ) А ׀В ׀истинная величина (длина)
прямой AB.
15
16.
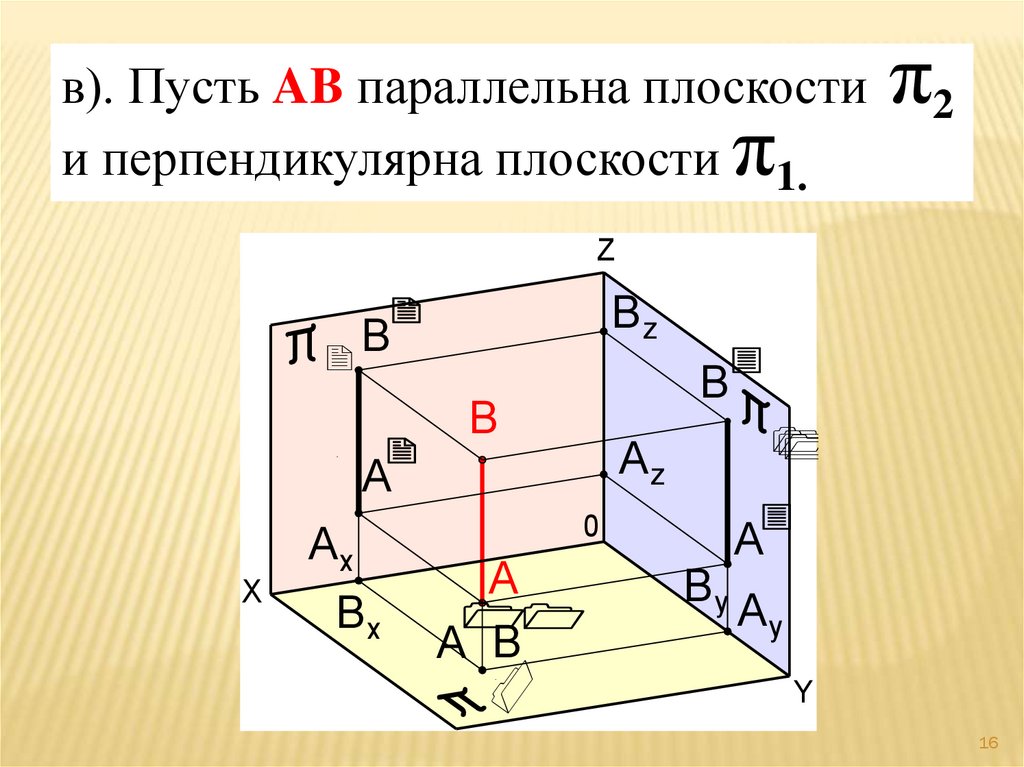
в). Пусть AB параллельна плоскостии перпендикулярна плоскости 1.
π
π2
Z
Вz
B
B
В
Вх
0
А
А В
Х
Аz
А
Ах
Вy
A
Аy
Y
16
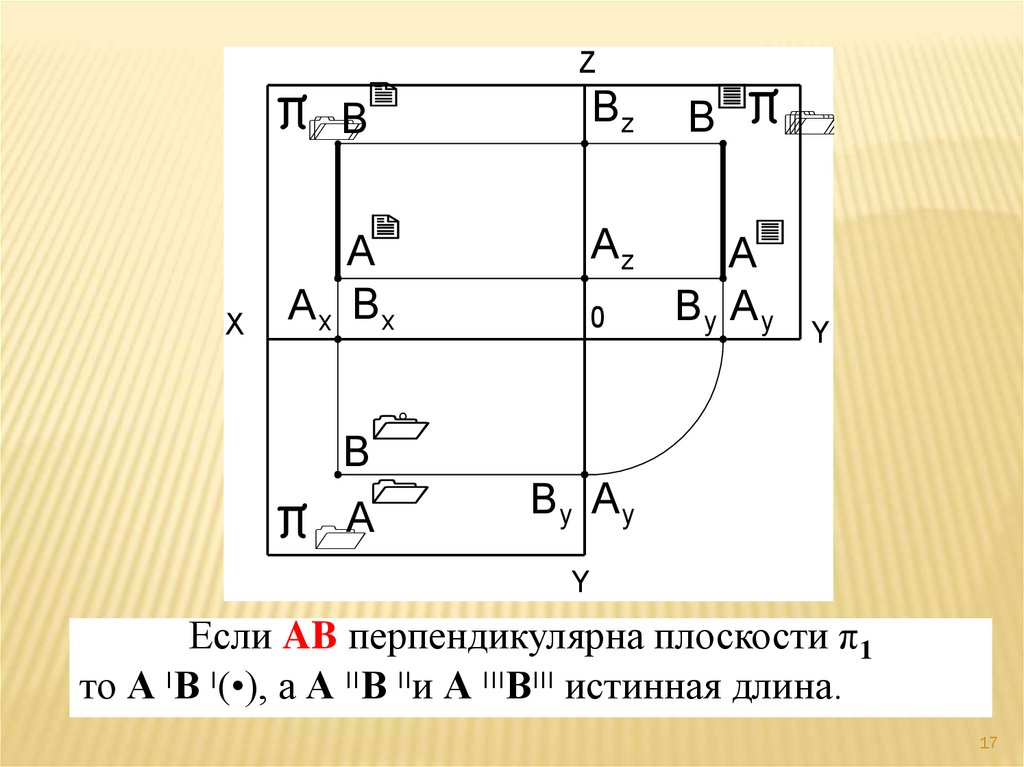
17.
BZ
Вz
Х
Аz
А
Ах Вх
0
B
A
Вy Аy
Y
В
А
Вy Аy
Y
Если AB перпендикулярна плоскости π1
то А ׀В )•(׀, а А ׀׀В ׀׀и А ׀׀׀В ׀׀׀истинная длина.
17
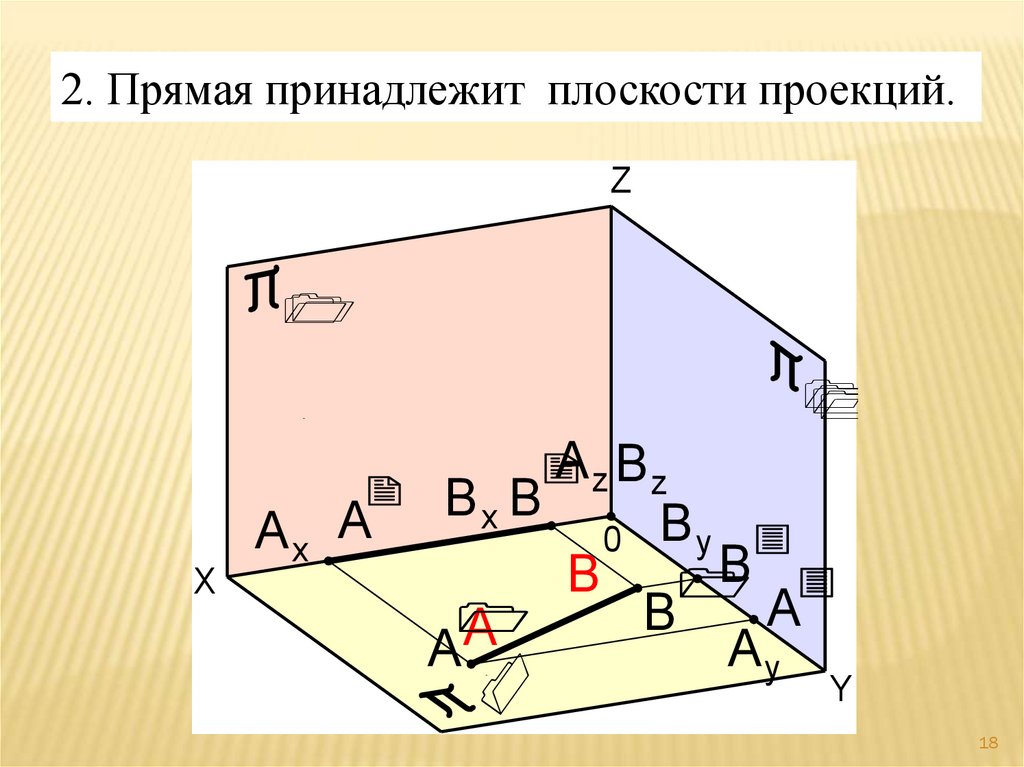
18.
2. Прямая принадлежит плоскости проекций.Z
Х
Ах А
Вх B
А
А
Аz Вz
В
0
Вy
B
В
A
Аy
Y
18
19.
ZХ
Ах А
А
В
B
А
Вх
A
z zB
0
Вy Аy
В Вy
Y
Аy
Y
19
20.
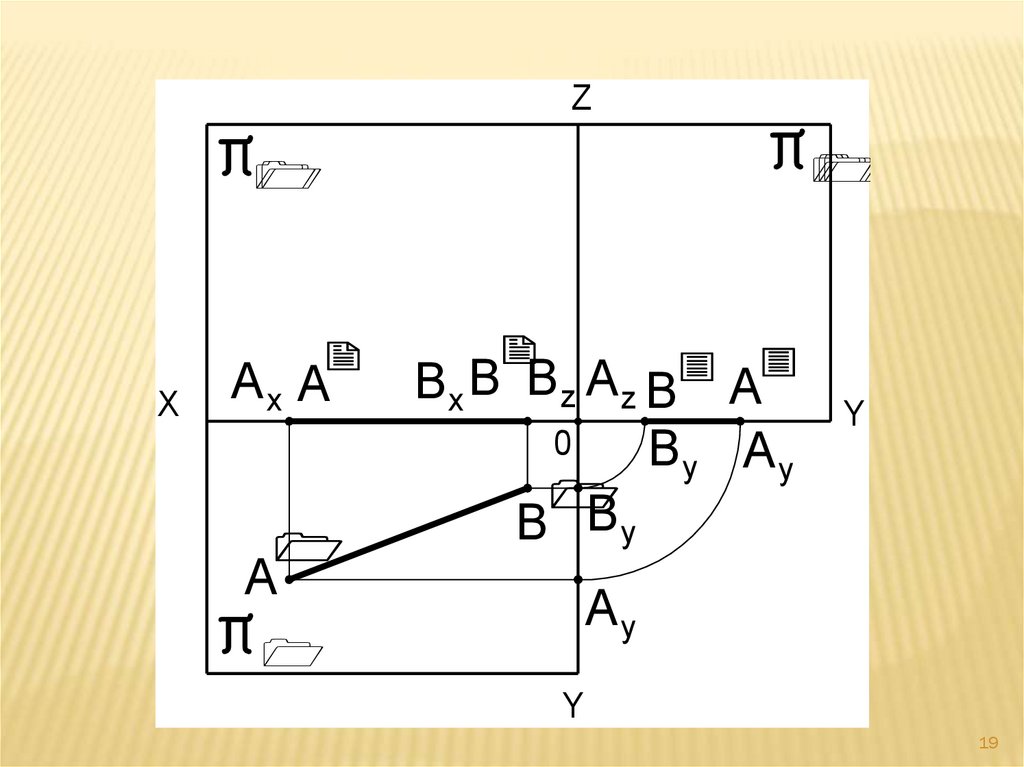
Если прямая принадлежит плоскостипроекций, то одна из проекций также
принадлежит этой плоскости, а две
другие проекции лежат на осях
координат:
AB = А ׀В׀
20
21.
ZХ
А
А
Ах А
Аy В
y
В Аz
В
z
B
A
B
0
Вх В
Y
21
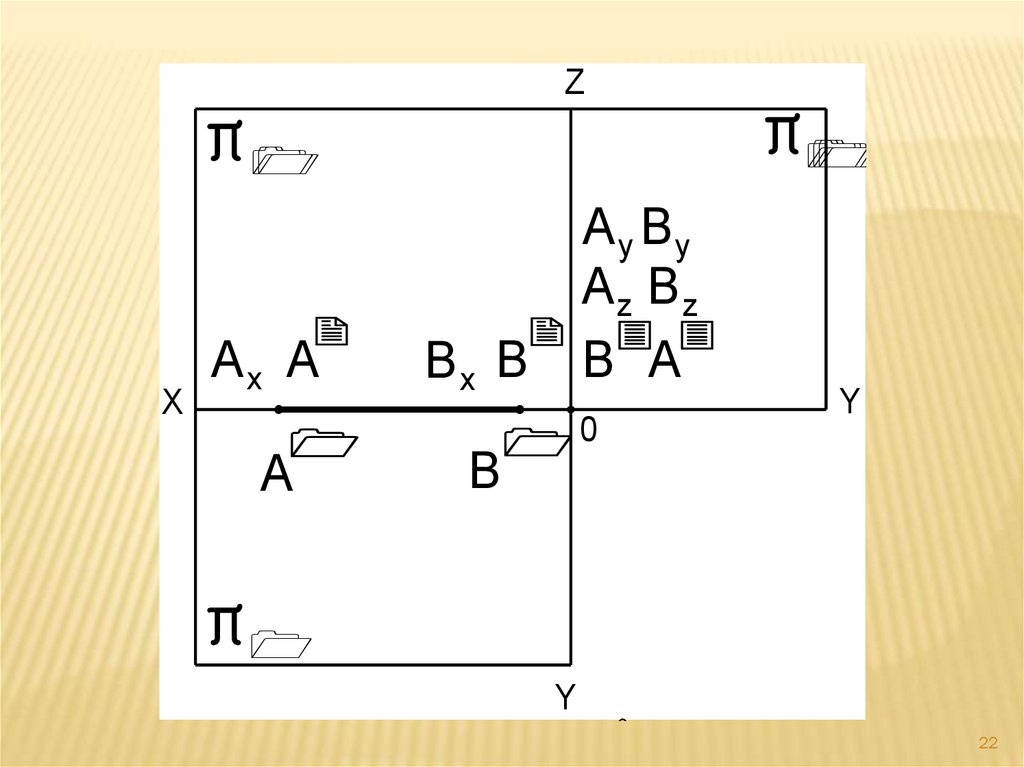
22.
ZХ
Ах А
А
Вх B
Аy Вy
Аz Вz
B A
0
Y
В
Y
22
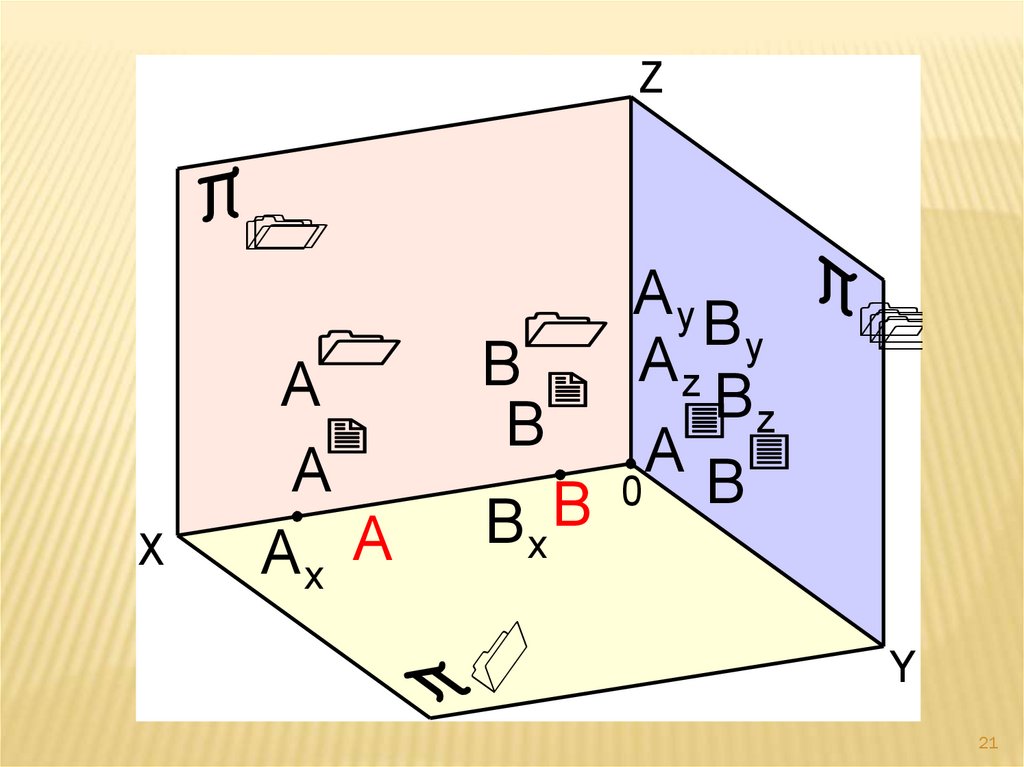
23.
Если прямая AB совпадает с осьюкоординат, то две её проекции А ׀В ׀и
А ׀׀В ׀׀совпадают с самой прямой AB ,
а третья проекция А ׀׀׀В ׀׀׀находится в
начале координат.
23
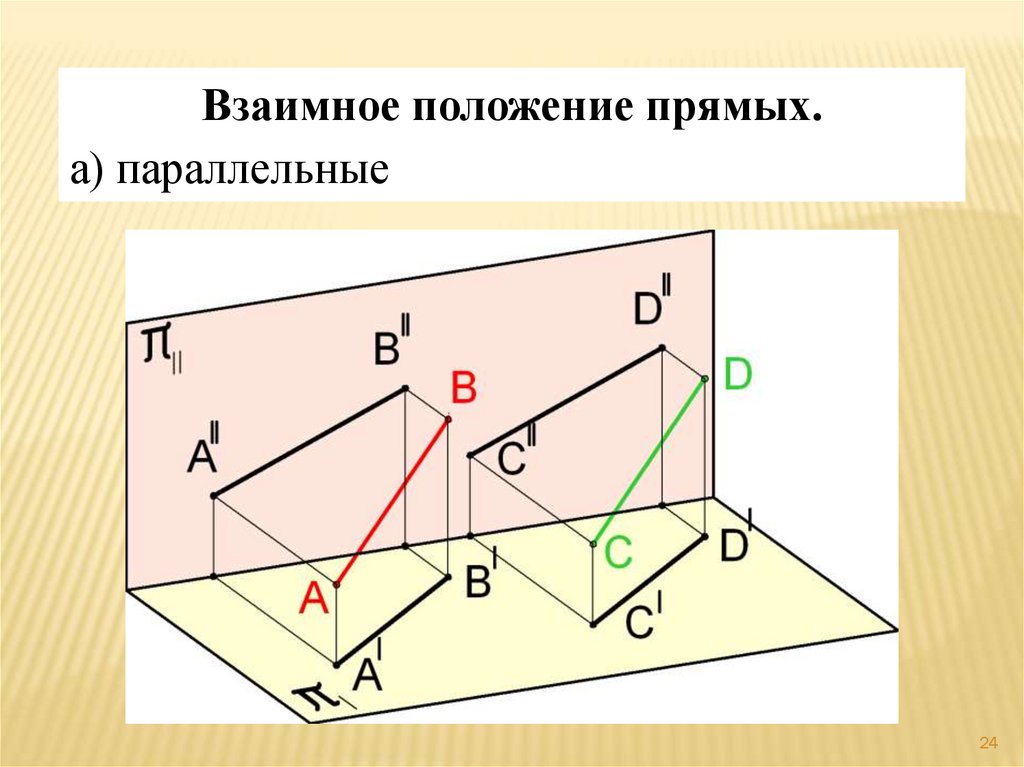
24.
Взаимное положение прямых.а) параллельные
24
25.
BА
Х
D
C
0
В
Аl
С
D
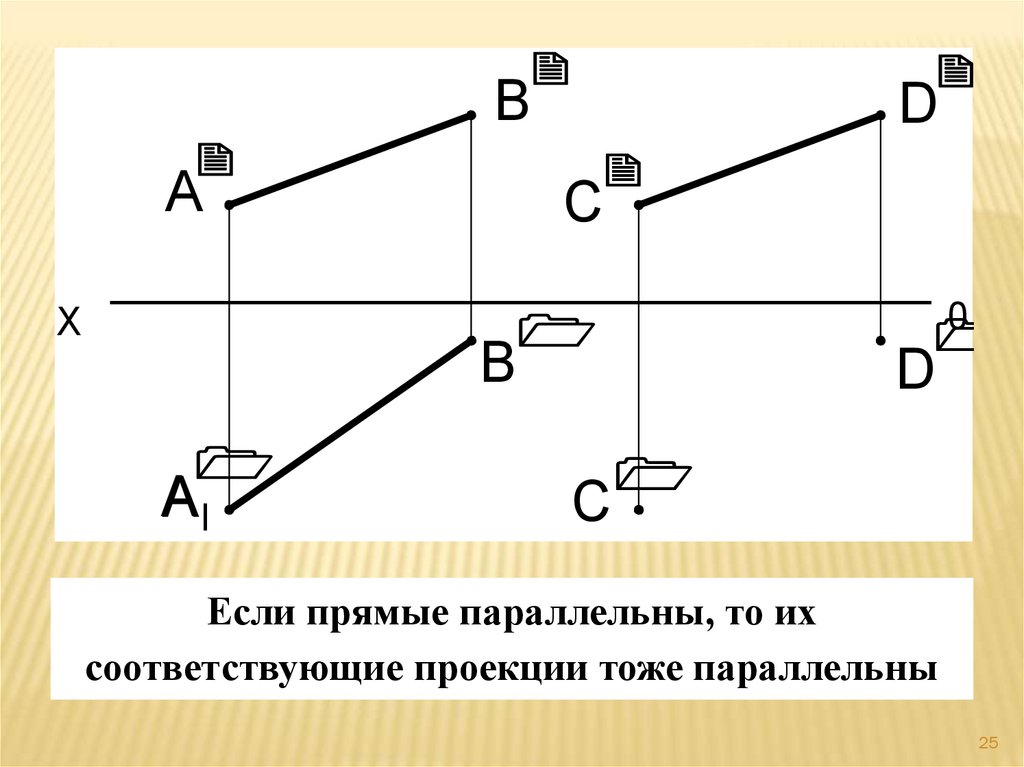
Если прямые параллельны, то их
соответствующие проекции тоже параллельны
25
26.
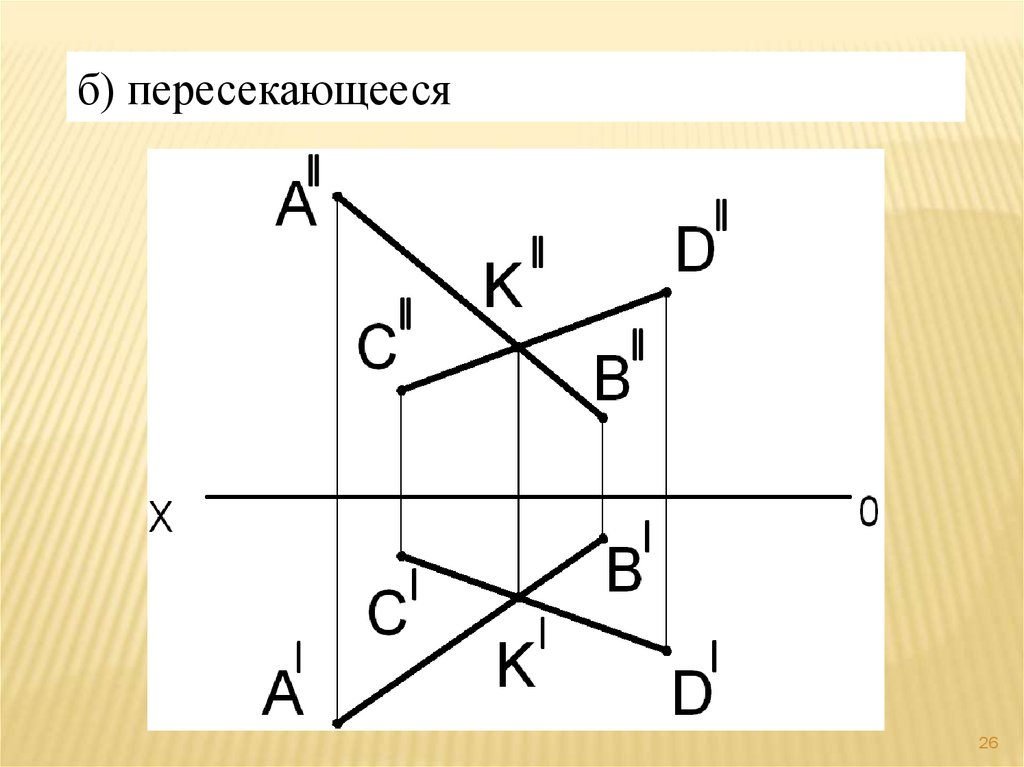
б) пересекающееся26
27.
У пересекающихся прямыхсоответствующие проекции А ׀В ׀, С ׀D׀
и А ׀׀В׀׀, С ׀׀D ׀׀пересекаются, а
проекции точки пересечения К ׀К׀׀
находятся на одном перпендикуляре к
оси координат.
Если прямые пересекающееся, то К
принадлежит обеим прямым проекции.
27
28.
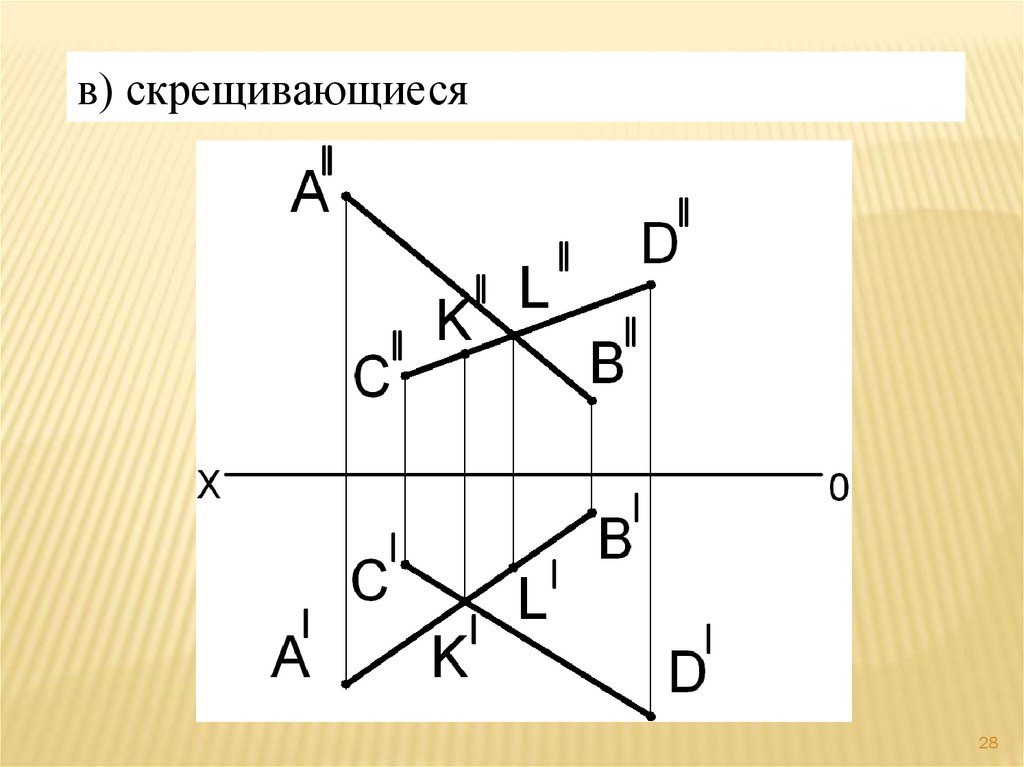
в) скрещивающиеся28
29.
Скрещивающиеся прямые не имеют общейточки. Их проекции могут пересекаться, но
точки пересечения К ׀К ׀׀и L ׀L ׀׀не
находятся в проекционной связи, т.е. не
лежат на одном перпендикуляре к оси
координат,
(•)К принадлежит CD,
(•)L принадлежит АВ.
29












 drafting
drafting








