Similar presentations:
Электронный курс "Линейная алгебра"
1.
ЛИНЕЙНАЯ АЛГЕБРАPowerpoint Templates
2.
ОГЛАВЛЕНИЕ1
2
3
• ЛЕКЦИИ
• ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
• СПИСОК ЛИТЕРАТУРЫ
3.
ЛЕКЦИИМатрицы. Действия над
матрицами
Определители
Обратная матрица
Системы линейных уравнений
4.
5.
Определение 1. Прямоугольная таблица из m строк и n столбцов,заполненная некоторыми математическими объектами, называется
прямоугольной матрицей.
Числа, составляющие матрицу, называются ее элементами.
а11 а12
а21 a22
... ...
a
m1 am 2
... а1n
... a2 n
... ...
... aтn
(1)
При записи, в общем виде элементы матрицы обозначаются одной
буквой с двумя индексами, из которых первый указывает номер строки, а
второй – номер столбца матрицы.
В сокращенной записи: A aij ;
(кратко i 1,2,..., m ,
j 1,2,..., n ).
i 1, m j 1, n
6.
Выражение m n называют размерностью матрицы.Матрица называется квадратной порядка n, если число ее строк равно
числу столбцов и равно n:
а11 а12
а21 a22
... ...
a a
n1 n 2
... а1n
... a2 n
... ...
... ann
Размерность квадратной матрицы записывают одним числом, которое
называется порядком матрицы.
Упорядоченный набор элементов a11 , a 22 ,..., a nn называется главной
диагональю, в свою очередь, a1n , a 2,n 1 ,..., a n1 – побочной диагональю
матрицы.
7.
Квадратная матрица, элементы которой удовлетворяют условию:аij 0, i j
aij
aij 0, i j ,
называется диагональной, т.е. диагональная матрица имеет вид:
а11
0
...
0
0
a22
...
0
0
... 0
... ...
... ann
...
Диагональная матрица порядка n называется единичной, если все
элементы ее главной диагонали равны 1. Матрица любого размера
называется нулевой или нуль матрицей, если все ее элементы равны
нулю. Единичная матрица обозначается буквой Е, нулевая – О. Матрицы
имеют вид:
1 0 ... 0
0 0 ... 0
0
1
...
0
0
0
...
0
E
О
... ... ... ...
... ... ... ...
0 0 ... 1
0 0 ... 0
8.
Определение 2. Две матрицы называются равными, если равны ихразмерности и равны их соответствующие элементы, т.е. элементы,
расположенные на пересечениях строк и столбцов с одинаковыми
номерами в обеих матрицах.
Матрица, состоящая из одной строки a1 , a 2 ,..., a n
, называется
матрицей-строкой.
a1
a2
Матрица, состоящая из одного столбца , называется матрицей...
столбцом.
a
n
9.
Определение 1. Суммой матриц А=(аij) и B=(bij) одинаковых размеровm n называется матрица С=(сij) тех же размеров, такая что cij=aij+bij для
всех i и j.
a11 b11
...
С А В
a b
m1 m1
a12 b12
a1n b1n
...
...
...
am 2 bm 2 .. ... amn bmn
.
...
Таким образом, чтобы сложить матрицы А и В, достаточно сложить
их элементы, стоящие на одинаковых местах.
10.
1 24 4
, В
А
3 4
0 1
1 2 4 4 1 4 2 4 5 2
+
.
A B
3 4 0 1 3 0 4 1 3 5
11.
Свойства операции сложения матрицПусть A, B, C – матрицы одинаковой размерности:
1. A+ B= B+A – коммутативность сложения;
2. (A+B)+C= A+(B+C) – ассоциативность сложения;
3. A+O=A;
Матрица О, состоящая из нулей, играет роль нуля.
4. A+(-A)=O.
Для любой матрицы существует противоположная,
будем ее обозначать -А, элементы которой отличаются
от элементов А знаком.
12.
Разность матриц А и В можно определить равенствомА-В=А+(-1)В.
Например
1 2
4 4
А
, В
3 4
0 1
1 2 4 4 1 4 2 ( 4) 3 6
.
A B
4 1 3 3
3 4 0 1 3 0
13.
Определение 2. Произведениемматрицы А на число
называется матрица А=( аij), получаемая умножением всех элементов
матрицы А на число .
а11
а
21
...
a
т1
Например
1 2 3 1 3 2 3 6
.
3
3 А=
3 4 3 3 3 4 9 12
а12
a 22
...
a т 2
... а1 n
... a 2 n
.
... ...
... a тn
14.
Свойства умножения матрицы на числоПусть А,В – матрицы одинакового размера; , - действительные
числа:
1. ( А) = ( )А = ( А) – ассоциативный закон;
2. ( + )А = А+ А – дистрибутивный закон (для чисел);
3. (А+В) = А+ В – дистрибутивный закон (для матриц);
4. 1* А = А;
5. 0 * А = О.
15.
Определение 3. Произведением матрицы А=(аij) размераm k и
прямоугольной матрицы B=(bij) размера k n называется прямоугольная
матрица С=(сij) размера m n , такая что
cij=ai1+b1j+ ai2+b2j+…+ aik+bkj;
i 1, m
,
j 1, n .
Таким образом, элемент произведения матриц А и В, стоящий в i-ой
строке и j-ом столбце, равен сумме произведений элементов i-ой строки
первой матрицы А на соответствующие элементы j-ого столбца второй
матрицы В т.е.
b1 j
b2 j
cij (ai1ai 2 aik )
.
b
kj
16.
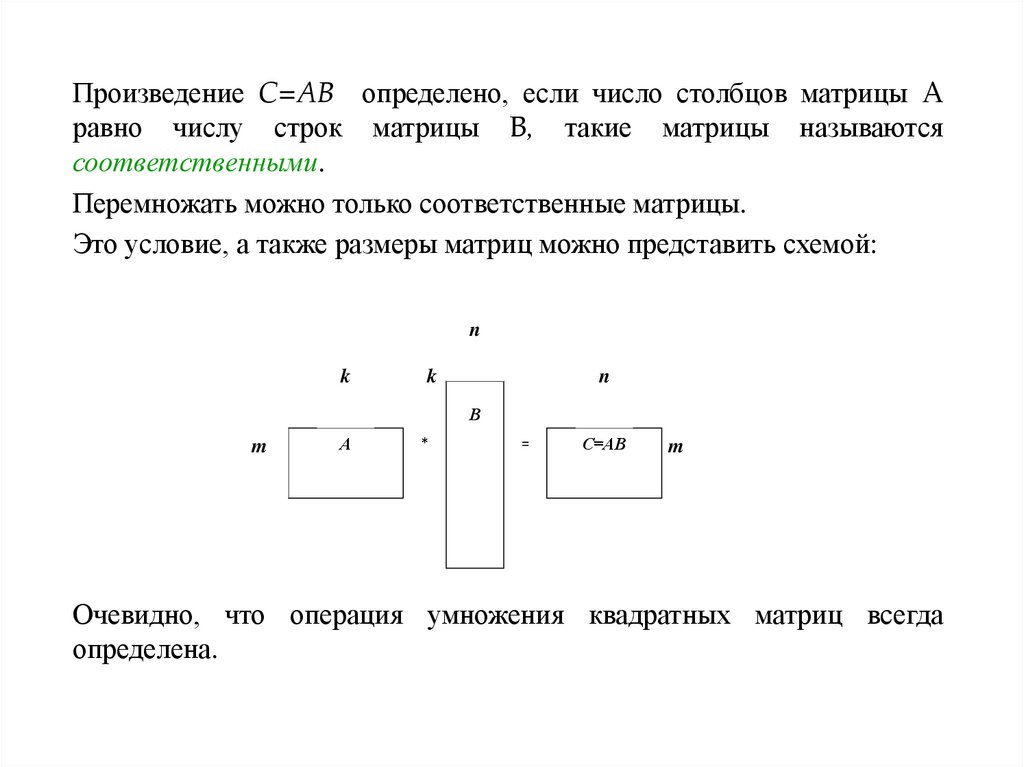
Произведение C=AB определено, если число столбцов матрицы Aравно числу строк матрицы B, такие матрицы называются
соответственными.
Перемножать можно только соответственные матрицы.
Это условие, а также размеры матриц можно представить схемой:
n
k
k
n
В
m
А
*
=
С=АВ
m
Очевидно, что операция умножения квадратных матриц всегда
определена.
17.
Например1 2 4 4 1 4 2 0 1 ( 4) 2 1 4 2
.
А В=
3
4
0
1
3
4
4
0
3
(
4
)
4
1
12
8
4 4 1 2 4 1 4 3 4 2 4 4 4 12 8 16 8 8
.
В А=
0
1
0
1
1
3
0
2
1
4
0
3
0
4
3
4
3
4
18.
Свойства умножения матриц1. Коммутативный (переместительный) закон умножения матриц,
вообще говоря, не выполняется, т.е. А В В А.
В частном случае коммутативным законом обладает произведение
любой квадратной матрицы
n-го порядка на единичную матрицу
такого же порядка, т.е. АЕ ЕА .
Матрицы называются перестановочными, если выполняется закон
коммутативности, т.е. AB =BA .
Пусть A,B,C – матрицы соответствующих размеров (т.е. произведения
матриц определены), - действительное число. Тогда на основании
определений операций и свойств действительных чисел имеют место
следующие свойства:
2. АB С А BC – ассоциативность;
Справедливы следующие законы дистрибутивности:
3. А B С АС BС - правый закон дистрибутивности ;
4. А B C АB АС - левый закон дистрибутивности;
5. АB А В А В ;
6.
ЕА АЕ А .
19.
Определение 4. Если A – матрица размерностиа11 а12
а21 a22
... ...
a
m1 am 2
m n :
... а1n
... a2 n
... ...
... aтn
то
транспонированием
этой
матрицы
называется
такое
преобразование, при котором ее строки становятся столбцами с теми же
номерами и наоборот, т. е. переход к следующей матрице размерности
n m :
а11 а21 ... аm1
a22 ... am 2
а
Т 12
.
... ... ... ...
a
1n a2 n ... amn
Данная матрица называется транспонированной матрицей.
Эта операция имеет общий характер, т. е. применима к любой матрице.
20.
21.
Дляобозначения
определителя
следующими обозначениями:
D ( A)
детерминант
A или aij
дельта
пользуются
22.
Числа, составляющие определитель, называются его элементами.(1)
При
записи,
в
общем
виде
элементы
определителя
обозначаются одной буквой с двумя индексами, из которых первый
указывает номер строки, а второй – номер столбца матрицы.
В сокращенной записи:
числа, i,j=1,…,n.
;
где
- действительные
23.
Главная диагональПобочная диагональ
Число строк равное числу столбцов и равное n
называется порядком определителя.
Упорядоченный набор элементов
а11,а22,…,аnn называется главной диагональю, в свою
очередь, а1n,а2,n-1,…,аn1 – побочной диагональю.
24.
Определителем первого порядкаA = a11
называют число a11 .
25.
Главная диагональA
a11
Побочная диагональ
a12
a21 a22
a11a22 a12 a21
26.
Например:A
2 1
4
5
2 5 ( 1) 4 14.
27.
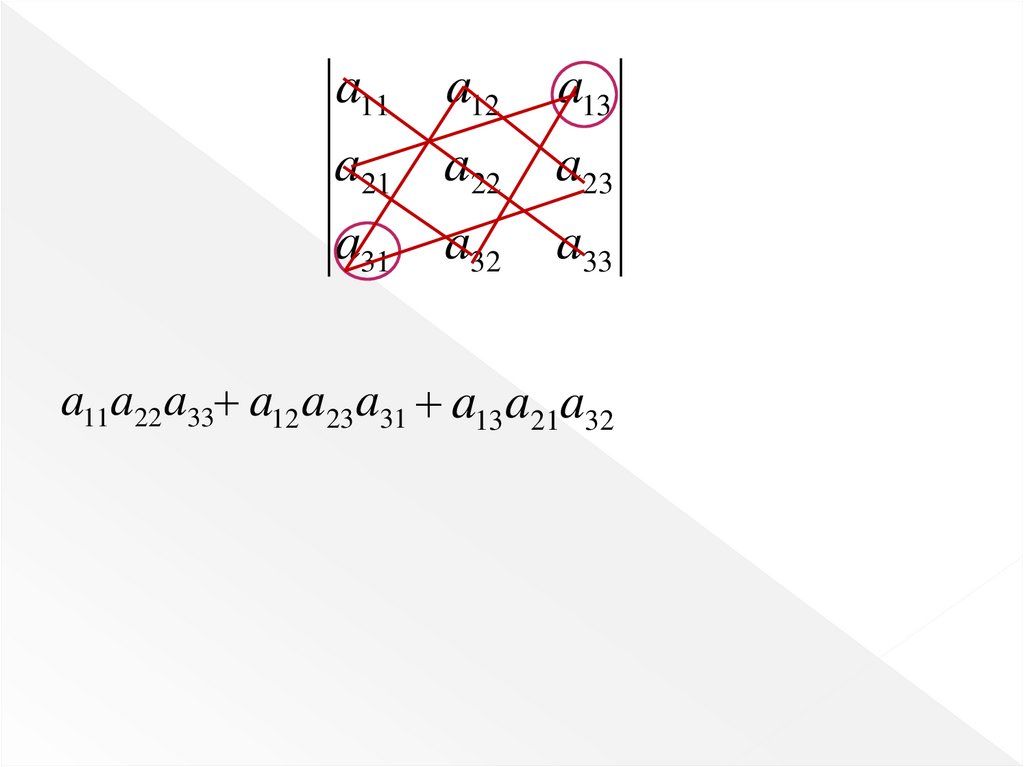
Формула вычисления определителя третьего порядка,которая называется правилом треугольников (правилом
Саррюса)
a11
A
a12
a13
a21 a22
a23
a31
a33
a32
28.
a11a12
a13
a21
a22
a23
a31
a32
a33
a11a22 a33 a12 a23 a31 a13 a21a32
29.
Рассмотрим первую группу слагаемых. Первое слагаемое– это произведение всех элементов главной диагонали
определителя, а в каждом из следующих множители образуют
в определителе треугольники, у которых одна сторона
параллельна главной диагонали:
*
a12
a13
a11
*
a21
*
a23
a 21
a 22
*
a32
a31 a32
*
,
a13 a11 a12 *
*
* a 22 a 23 .
,
a33 a31 * a33
30.
a11a12
a13
a21
a22
a23
a31
a32
a33
a13 a22 a31 a12 a21a33 a11a23a32
31.
Слагаемые,которые
иллюстрируются
имеют
аналогично,
знак
только
минус,
вначале
перемножаются все элементы побочной диагонали, а затем
выбираются такие тройки элементов определителя, которые
образуют треугольники со стороной, параллельной его
побочной диагонали:
a11
a12
a 21
*
*
a32
*
a12
a13
a11
*
a13
a 23 a21
,
a33 a31
a22
*
*
a22
a23 .
*
a33
*
,
a31 a32
*
32.
a11a12
a13
A a21 a22 a23
a31
a32
a33
a11a22 a33 a12 a23 a31 a13 a21a32 a13 a22 a31 a12 a21a33 a11a23 a32
33.
Например:1 3
2
А 0 5 1
4 6
7
1 5 7 2 0 6 3 ( 1) 4
2 5 4 3 0 7 1 ( 1) 6 11
.
34.
Перейдемтеперь
к
формулированию
понятия
определителя любого порядка n (n 2) .
Понятие такого определителя мы введем индуктивно,
предполагая, что нам уже известно, как находятся
определители всех квадратных матриц, порядок которых
строго меньше n.
35.
Рассмотрим произвольную квадратную матрицу порядка n:a11 a12
a21 a22
... ...
ai1 ai 2
... ...
a
n1 an 2
Выберем в
A
... a1 j
... a2 j
...
...
...
aij
...
...
... anj
... a1n
... a2 n
... ...
(4).
... ain
... ...
... ann
любой элемент a ij и вычеркнем из
A
i- строку и
j- столбец. Из оставшихся элементов, не меняя их взаимного
расположения, составим матрицу. Это будет квадратная матрица
порядка (n-1). По индуктивному предположению, мы умеем
находить определитель полученной матрицы. Обозначим его M ij и
назовем минором элемента a ij .
36.
Определение2.
Минором
элемента
a ij
называется
определитель (n-1) – порядка, полученный путем вычеркивания i –
строки и j– столбца.
Например:
A
1
0
3
7
2
3
7
1
0
2
3 1
1
1 2
4
.
37.
Определение 3. Определителем порядка n, соответствующимматрице (4), называется число, равное
n
1 j
A 1 a1 j M 1 j .
j 1
(5)
Формула (5) при вычислении определителя использует все
элементы первой строки (разложение определителя по первой
строке).
38.
Теорема 1. При любом номере строки i( i = 1,2, ...,n), для определителя nгo (n 2) порядка матрицыA (4) справедлива формула
i j
n
A 1 aij M ij ,
i 1
(6)
называемая разложением этого определителя по i-й строке.
Теорема 2. При любом номере столбца j ( j =(,2,…,n), для определителя nго (n 2) порядка матрицы A (4) справедлива формула
n
i j
A 1 aij M ij .
j 1
(7)
39.
Например:1
1 2 2
0
0
A 1 0
1
0
1
1
1
1 3
0
1 1
2 4
1
1 2
1
0
1
1 3
1 1.
40.
Определение 4. Пусть дан определительцелое
число
k,
удовлетворяющее
A
порядка n. Выберем
условию
1 k n 1,
и
в
определителе A выберем произвольные k строк и k столбцов.
Элементы, стоящие на пересечениях выбранных строк и столбцов,
очевидно составляют квадратную матрицу порядка k. Определитель
этой матрицы называется минором k-го порядка определителя A .
a11
a12
... a1 j
... a1k
... a1n
a21
a22
... a2 j
... a2 k
... a2 n
...
...
...
...
...
...
ai1
ai 2
...
aij
... aik
... ain
...
...
...
...
...
...
ak 1
ak 2
... akj
... akk
... akn
...
...
...
...
...
an1
an 2
... anj
...
...
...
...
... ank
...
...
...
... ann
(8).
41.
Пусть в определителеA порядка
n выбран минор М k-го
порядка. Вычеркнем те строки и столбцы, на пересечениях которых
расположен этот минор.
Оставшиеся элементы образуют квадратную матрицу порядка
(n-k), определитель которой называется дополнительным к минору
М и обозначается М'. Если мы вычеркнем, наоборот, те строки и
столбцы, в которых расположены элементы минора М', то,
очевидно, останется минор М. Таким образом можно говорить о
паре взаимно дополнительных миноров определителя. В частности,
определенный выше минор M ij является дополнительным к минору
первого порядка
a ij
и наоборот.
42.
Определение 5. Если минор k-го порядка М расположен встроках с номерами i1 , i2 ,..., ik и в столбцах с номерами
j1 , j 2 ,..., j k ,
то
образуем сумму
SM
= i1 i2 ... ik j1 j2 ... jk .
(9)
Алгебраическим дополнением для минора М будем называть
SМ
(
1
)
M .
число
В частности, алгебраическим дополнением элемента Àij будет
число
Aij ( 1) SМ M ij .
n
A
i 1
aij Aij
(10)
n
j 1
aij Aij .
(11)
43.
Например:1 0 3 4
A
5
2 3 4 5
6
5
2 1 6
1 2 3
2 1
4 2 3 4 280.
6
1 2
2 1 6
5
2 6
( 1) A11 0 A12 3 A13 4 A14 3 4 5 3 2 3 5
1 2 3
6 1 3
44.
Теорема 3 (Лапласа). Пусть в определителепроизвольно выбраны k строк (или k столбцов),
A
порядка n
1 k n 1.
Тогда
сумма произведений всех миноров k-го порядка, содержащихся в
выбранных
строках
(или
столбцах),
дополнения равна определителю A .
на
их
алгебраические
45.
Например:4
1
2
2
1
0
3
0
1
5
1
3
1
3
1
0
0
2
5
A 2 3
1 1
0
4
Разлагая определитель по первому и третьему столбцам, содержащим
„удачно" расположенные нули, мы получим:
A 1
1 3 1 3
1 3 4 1 3
2
1
1 3
4 2
2
1
1 2
1
3
1
4
2
3
1
5
1 1 0 + 1
1 4 1 3
4
2
5
4 2
1 3
3
1
5
3 3 1 +
4
2
5
5 ( 8) ( 20) ( 10) ( 62) 7 87 1069.
5
46.
Свойства определителей n-го порядка1. Определитель матрицы
A
равен определителю транспонированной матрицы
AТ , т.е. определитель не меняется при транспонировании.
2. Если одна из строк (один из столбцов) определителя состоит из нулей, то
определитель равен нулю.
3. Определитель, содержащий две одинаковые строки или два одинаковых
столбца, равен нулю.
4.
Определитель,
содержащий
две
пропорциональные
строки
(два
пропорциональных столбца), равен нулю.
5. Если все элементы некоторой строки (столбца) определителя умножить на
некоторое число k, то сам определитель умножится на k.
6. Если все элементы i-й строки определителя n-гo порядка представлены в
виде суммы двух слагаемых: aij b j c j , j =1,2, ...,n, то определитель равен сумме
двух определителей 1 и 2 , у которых все строки, кроме i-й, такие же, как и в
47.
7. Определитель не меняется, если к элементам одной из его строк (столбцов)прибавляются соответственно элементы другой строки (столбца), умноженные на
одно и то же число.
8. Сумма произведений всех элементов некоторой строки определителя на
алгебраические дополнения соответствующих элементов другой строки равна нулю.
9.
Определитель
произведения
двух
квадратных
матриц
размерностей равен произведению определителей этих матриц:
одинаковых
48.
49.
МатрицаВырожденная
(особенная)
определитель равен
нулю
Например:
2 3
А
4 6
А 12 12 0
Невырожденная
(неособенная)
определитель отличен
от нуля
Например:
4 3
А
5 4
А 16 15 1 0
50.
Теорема 1. Произведение матриц есть вырожденнаяматрица тогда и только тогда, когда хотя бы один из
множителей есть вырожденная матрица
Замечание. Данная теорема справедлива для
любого числа множителей.
51.
Определение. Квадратная матрица В называетсяобратной по отношению к матрице А такого же
размера, если
АВ = ВА = Е.
(1)
52.
Теорема 1. Если для данной матрицы обратная существует,то она определяется однозначно.
Теорема
2
(необходимое
и
достаточное
условие
существования обратной матрицы). Обратная матрица А-1
существует тогда и только тогда, когда исходная матрица А
невырожденная.
53.
Теорема 2 (необходимое и достаточное условие существованияобратной матрицы). Обратная матрица А-1 существует тогда и только
тогда, когда исходная матрица А невырожденная.
Доказательство.
Необходимость.
Дано: для матрицы А существует обратная А-1.
Доказать: А – невырожденная.
Доказательство:
Для матрицы А существует обратная А-1, т.е.
А
А-1 = А-1 А = Е.
Тогда, А А-1 = А А-1 = Е =1, т.е. А 0 и
А-1 0;
А – невырожденная.
54.
Теорема 2 (необходимое и достаточное условие существованияобратной матрицы). Обратная матрица А-1 существует тогда и только
тогда, когда исходная матрица А невырожденная.
Доказательство.
Достаточность.
Дано: невырожденная матрица порядка n
а11 a12
а21 a22
А
аn1 an 2
так что ее определитель
a1n
a2 n
,
ann
0.
Доказать: существует обратная матрица А-1.
55.
Рассмотримматрицу,
составленную
из
алгебраических
дополнений к элементам матрицы А:
A11 A 21
A12 A 22
А
A1n A 2 n
A n1
A n2
,
A nn
ее называют присоединенной к матрице А.
Следует обратить внимание на то, что алгебраические
дополнения к элементам i-ой строки матрицы А стоят в j-ом
столбце матрицы А*, для i 1, n .
56.
Найдем произведение АА*=С:a11
a21
C
...
a
n1
a12
...
a22
...
...
...
an 2
...
n
a1i A1i
i 1
n
a2i A1i
i 1
n ...
an1 A1i
i 1
a1n A11
a2 n A12
...
ann A1n
n
1i
A2i
...
a
2i
A2i
...
i 1
...
n
a
i 1
ni
...
A2i
A22
A2 n
...
An1
An 2
Ann
a1i Ani
i 1
n
a2i Ani
i 1
...
n
a
A
ni
ni
i 1
.
n
a
i 1
n
A21
57.
На главной диагонали получим суммы произведений элементовk-той строки матрицы А ( k 1,n ) на алгебраические дополнения элементов этой же строки, такие суммы равны определителю матрицы А,
т.е. . На всех других местах имеем суммы произведений элементов
некоторой строки матрицы А на алгебраические дополнения элементов
другой строки. Такие суммы равны нулю. Таким образом, матрица С
имеет вид:
0
С
...
0
... 0
... 0
... ... ...
0 ... .
0
Аналогично доказывается, что произведение А* на А равно той же матрице С. Таким образом, имеем АА*=А*А = С.
58.
Отсюда следует, что1
1 1
А А А А С Е .
Поэтому, если в качестве обратной матрицы взять
1
А А 1 ,
то
1
1
А А А А Е .
59.
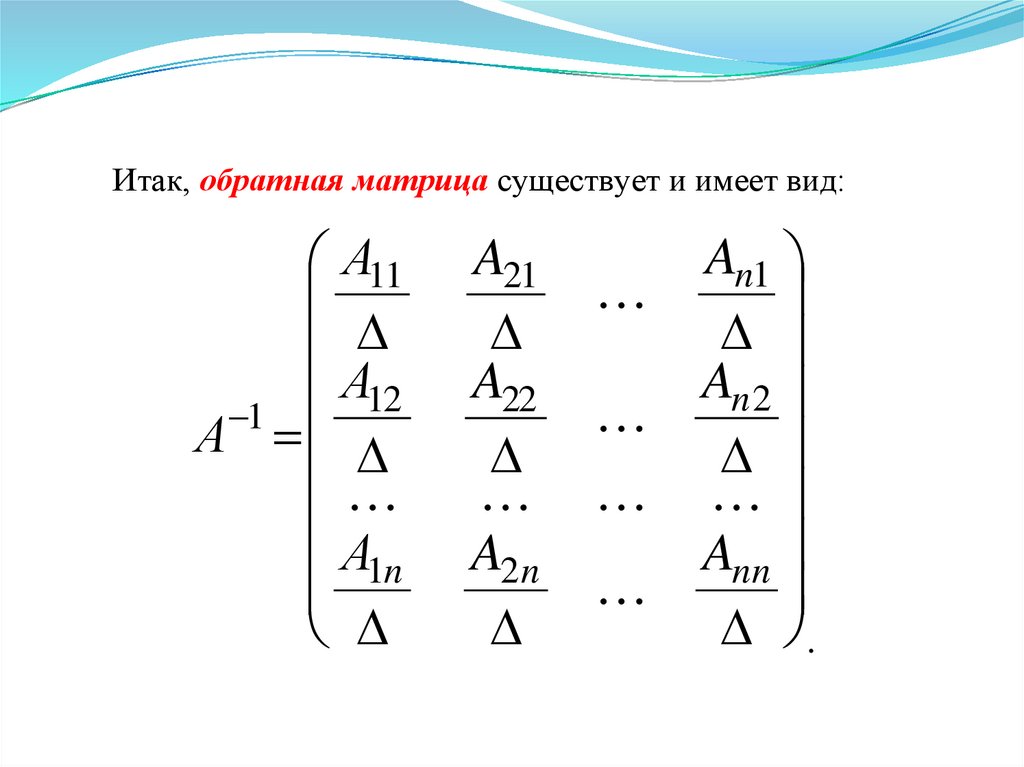
Итак, обратная матрица существует и имеет вид:А11
А12
1
А
А1n
A21
A22
A2 n
An1
An 2
Ann
.
60.
Таким образом, чтобы найти матрицу, обратную дляматрицы А, требуется:
1) вычислить ее определитель. Если А 0 - матрица А –
вырожденная, для нее обратной не существует. Если А 0 ,
то перейти к следующему пункту
2) составить присоединенную матрицу А .
3) найти произведение
1
А А 1
4) сделать проверку: А А 1 Е .
61.
Системы линейныхуравнений
1. Матричные уравнения
62.
Рассмотримпроизвольную
систему
линейных
уравнений
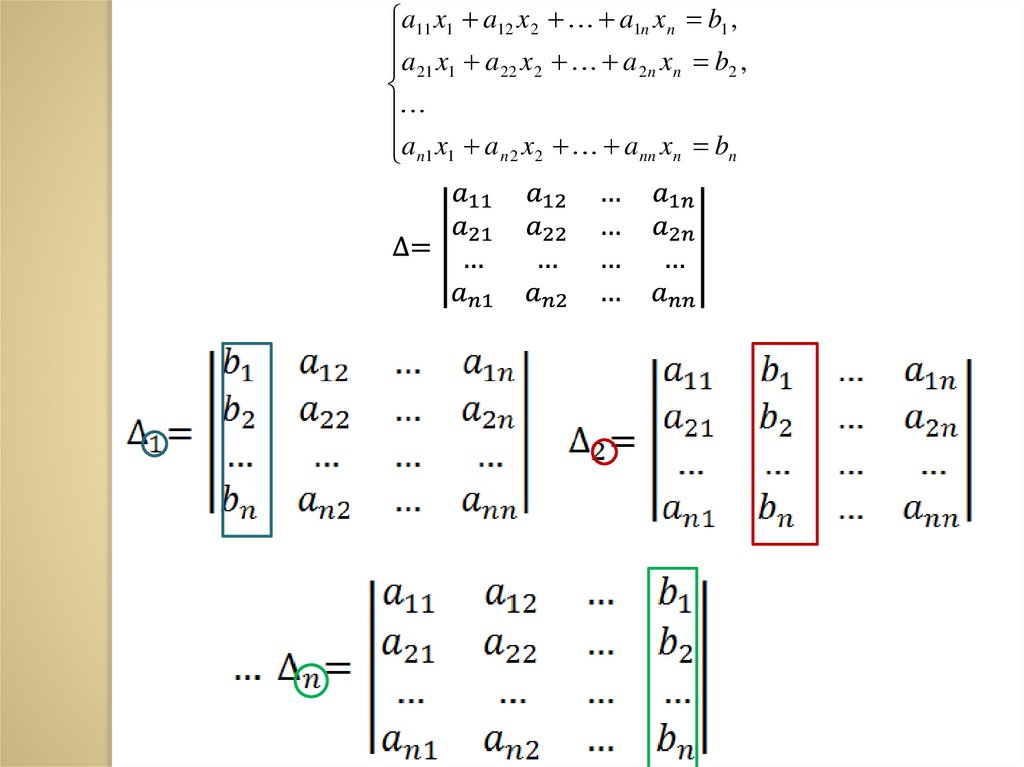
a11 x1 a12 x 2 a1n x n b1 ,
a x a x a x b ,
21 1
22 2
2n n
2
a m1 x1 a m 2 x 2 a mn x n bm
(2.1)
где x1 , x 2 ,..., xn — неизвестные переменные,
a11,..., amn
–
коэффициенты
при
b1 , b2 ,..., bm – свободные члены системы.
неизвестных,
63.
Определение 1. Любой числовой набор ( 1 , 2 ,..., n )называется
решением
системы
(2.1),
если
после
подстановки этих чисел в систему вместо соответствующих
неизвестных все уравнения системы обращаются в верные
числовые равенства (тождества):
b1 b1 , b2 b2 ,..., bm bm .
64.
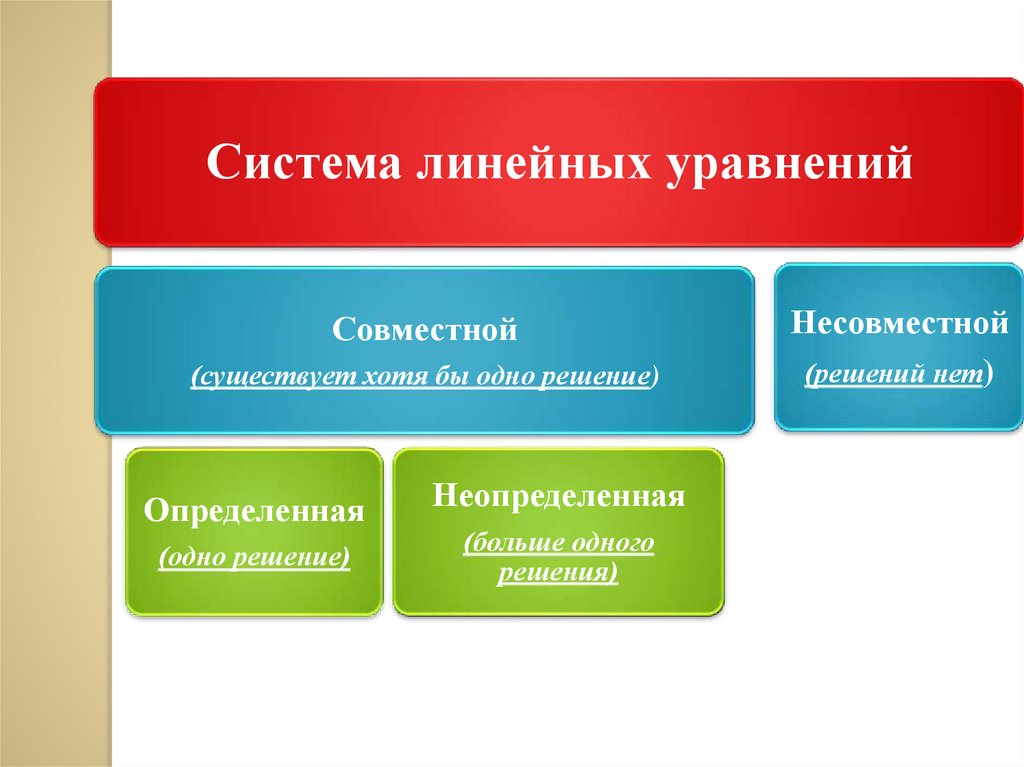
Система линейных уравненийСовместной
(существует хотя бы одно решение)
Определенная
(одно решение)
Неопределенная
(больше одного
решения)
Несовместной
(решений нет)
65.
Определение 2. Система линейных уравнений (2.1)называется совместной, если существует хотя бы одно ее
решение, в противном случае система несовместна.
Система называется определенной, если она имеет только
одно решение и неопределенной, если ее решений больше
одного.
Определение
3.
Решить
систему
линейных
уравнений – это значит найти все ее решения или доказать
несовместность системы.
66.
Часто бывает целесообразно заменить систему линейных уравненийэквивалентным матричным уравнением.
a11 x1 a12 x 2 a1n x n b1 ,
a x a x a x b ,
21 1
22 2
2n n
2
a m1 x1 a m 2 x 2 a mn x n bm
Для этого следует ввести матрицы:
а11 а12
а21 a22
... ...
a
m1 am 2
x1
... а1n
x2
... a2 n
X
... ;
... ... ;
x
... amn
n
b1
b2
B
... ,
b
m
где — основная матрица системы, X — столбец неизвестных и
B – столбец свободных членов системы.
Каждую систему вида (2.1) можно записать в виде одного
матричного уравнения:
АХ В .
(2.2)
67.
К матричным уравнениям относятся уравнения видаA X B
(2.2)
X A B
(2.3)
A X B C
(2.4)
где A, B, C , X матрицы.
Определение 4. Решением матричного уравнения
называется
матрица,
обращающая
уравнение в верное равенство.
при
подстановке
68.
Если в уравнениях (2.1), (2.2), (2.3) матрицы A, B, C - квадратные,порядка n, то решение может быть получено в виде:
A X B , A 0
A 1 A X A 1 B ,
A
1
A X A 1 B,
E X A 1 B,
X A 1 B.
(2.1.1)
X A B
X B A 1 ,
A 0
(2.2.2)
A X B C
X A 1 С B 1 ,
A 0 и
B 0.
(2.3.3)
69.
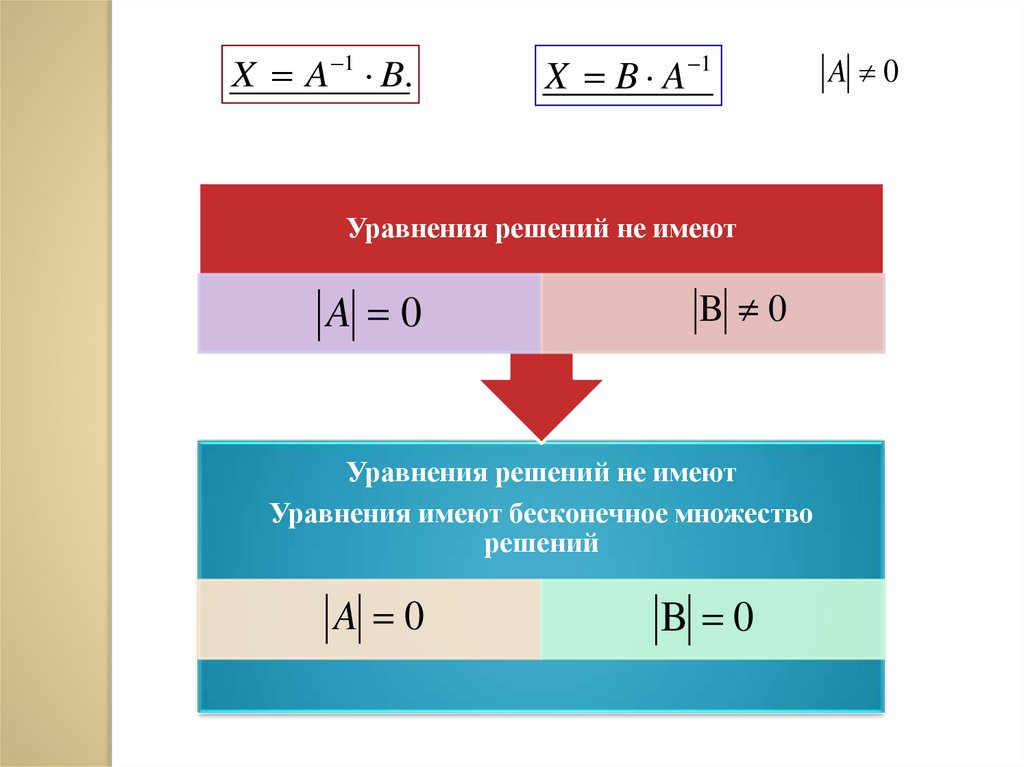
X A 1 B.X B A 1
Уравнения решений не имеют
A 0
B 0
Уравнения решений не имеют
Уравнения имеют бесконечное множество
решений
A 0
B 0
A 0
70.
2. Системы линейныхуравнений
2. Квадратные системы линейных
уравнений. Однородные системы.
Правило Крамера
71.
Рассмотримквадратную
систему
линейных
уравнений
a11 x1 a12 x 2 a1n x n b1 ,
a x a x a x b ,
21 1
22 2
2n n
2
a n1 x1 a n 2 x 2 a nn x n bn
(2.2.1)
где x1 , x 2 ,..., xn — неизвестные переменные,
a11,..., ann
–
коэффициенты
при
b1 , b2 ,..., bn – свободные члены системы.
неизвестных,
72.
Теоремаматрица
Крамера.
квадратной
Если
основная
системы
линейных
уравнений невырожденная, то такая система
имеет единственное решение.
73.
Теорема 1.4 (Крамера). Если основная матрица квадратной системылинейных уравнений невырожденная, то такая система имеет единственное
решение.
Доказательство.
a11 x1 a12 x 2 a1n x n b1 ,
a x a x a x b ,
21 1
22 2
2n n
2
a n1 x1 a n 2 x 2 a nn x n bn
а11 а12
а21 a22
... ...
a
n1 an 2
x1
... а1n
... a2 n
x2
X
...
... ... ;
;
x
... ann
n
b1
b2
B
... ,
b
n
где — основная матрица системы, X — столбец неизвестных и B –
столбец свободных членов системы.
Систему вида (2.2.1) можно записать в виде одного матричного
уравнения:
АХ В .
(2.2.2)
74.
Доказательство.Поскольку – невырожденная матрица, то
существует обратная матрица
А 1 .
Обе части
уравнения (2.2.2) умножим слева на А 1 и получим
решение системы в матричной форме
A X B , A 0
A A X A B ,
1
A
1
1
A X A 1 B,
E X A 1 B,
X A 1 B.
(2.2.3)
75.
Запишем формулу (2.2.3) в развернутом виде:X A 1 B.
x1
A11 A21
x2 1 A12 A22
..
A1n A2 n
x
n
xi
An1 b1
An 2 b2
...
Ann bn
1
b1 A1i b2 A2i bn Ani , i 1, n
Сумма в скобках правой части этого равенства есть
разложение определителя i , полученного из определителя
матрицы , заменой i-го столбца столбцом свободных членов.
76.
1xi b1 A1i b2 A2i bn Ani , i 1, n
i
xi
,
i 1, n .
(1.2.4)
Они получили название формул Крамера.
Решение системы (2.2.1) с применением формул
Крамера называют правилом Крамера.
77.
ixi
,
i 1, n
- основной определитель системы (определитель,
состоящий из коэффициентов при неизвестных ),
– определитель, полученный из определителя ,
заменой i-го столбца столбцом свободных членов.
78.
a11 x1 a12 x 2 a1n x n b1 ,a x a x a x b ,
21 1
22 2
2n n
2
a n1 x1 a n 2 x 2 a nn x n bn
79.
Определение.Линейное
уравнение
называется
однородным, если свободный член уравнения равен 0.
Система, состоящая из однородных уравнений, сама
называется однородной.
Общий вид однородной системы m уравнений с n
неизвестными:
a11 x1 a12 x 2 a1n xn 0,
a x a x a x 0,
21 1
22 2
2n n
a m1 x1 a m 2 x 2 a mn xn 0
(2.2.4)
80.
Однородная система всегда совместна: одно из еерешений есть
x1 0 , x2 0 ,…, xn 0 .
Это решение называется нулевым.
Особую важность представляет вопрос, имеет ли данная
однородная система ненулевые решения.
Теорема 1. Однородная система, в которой число
уравнений меньше числа неизвестных, всегда имеет ненулевое
решение.
Теорема 2. Если квадратная однородная система
линейных
уравнений
имеет
ненулевые
решения,
то
определитель ее основной матрицы необходимо равен
нулю.
81.
2. СИСТЕМЫ ЛИНЕЙНЫХУРАВНЕНИЙ
Метод Гаусса
(метод последовательного исключения
неизвестных)
82.
Определение. Две системы линейных уравнений с одними
тем
же
числом
неизвестных
называются
эквивалентными, или равносильными, если они обе
несовместны,
либо
обладают одними
и
теми
же
решениями, т. е. всякое решение одной системы является
решением другой и наоборот.
83.
СЛЕДУЮЩИЕ ПРЕОБРАЗОВАНИЯЛИНЕЙНЫХ УРАВНЕНИЙ БУДЕМ
ЭЛЕМЕНТАРНЫМИ:
СИСТЕМЫ
НАЗЫВАТЬ
-перемена местами любых двух уравнений системы;
-умножение обеих частей любого уравнения системы на
число, отличное от нуля;
-прибавление к любому уравнению системы любого
уравнения этой системы, умноженного на число;
- удаление из системы уравнений, у которых все
коэффициенты и свободный член равны нулю.
84.
ТЕОРЕМА 1.Применение
любого
элементарного
преобразования к системе линейных уравнений
приводит к эквивалентной системе.
85.
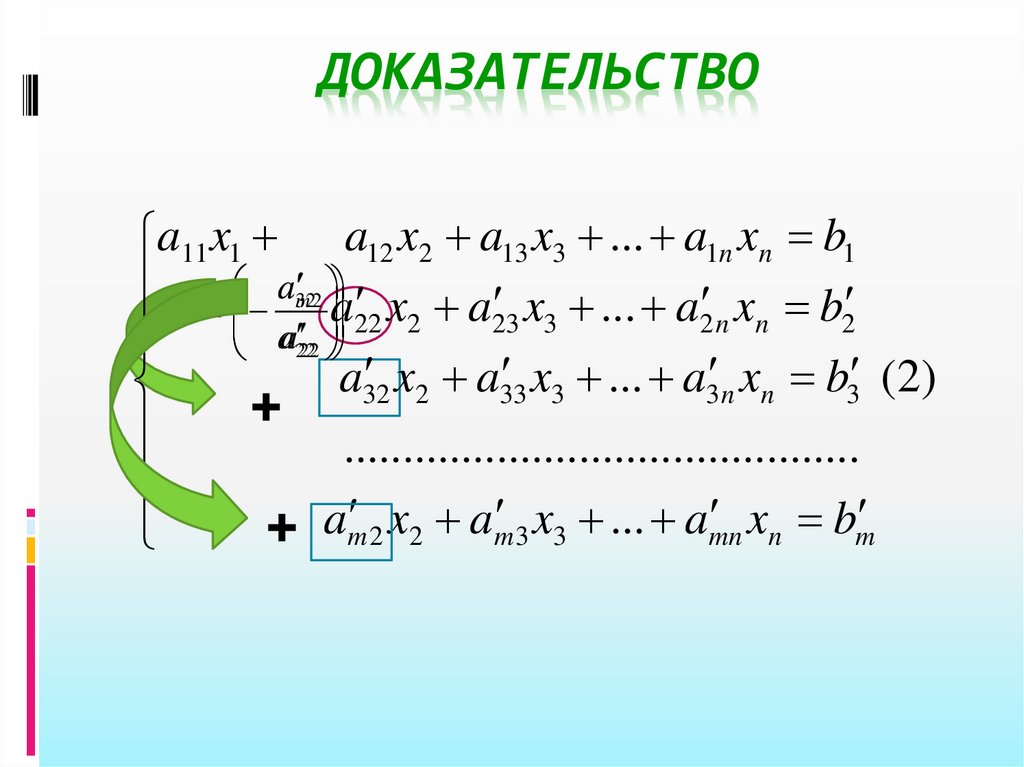
ДОКАЗАТЕЛЬСТВОa x a12 x2 a1n xn b1 ,
a x a x a x b ,
2n n
2
+ 21 1 22 2
+ a31 x1 a32 x2 ... a3n xn b3 , (1)
+ am1 x1 am 2 x2 amn xn bm
a31
m1
21
11 1
11
a11
86.
Мы считаем, что в системе n неизвестных, а потому длякаждого неизвестного в системе (1) имеется хотя бы один
коэффициент, отличный от нуля.
Тогда, если надо, переставив уравнения в системе и
переобозначив соответствующим образом коэффициенты, добьемся,
чтобы а11 0 .
Теперь исключим последовательно неизвестное x1 из всех
уравнений системы (1), начиная со второго. Для этого сначала обе
a21
части первого уравнения умножим на число a и прибавим к
11
соответствующим частям второго уравнения, затем обе части
первого
уравнения,
умноженные
на
a31
, прибавим к
a11
соответствующим частям третьего уравнения, и т. д.
87.
ДОКАЗАТЕЛЬСТВОa11 x1 a12 x2 a13 x3 ... a1n xn b1
x2 a23
x3 ... a2 n xn b2
a
22
x2 a33
x3 ... a3 n xn b3 (2)
a32
............................................
xn bm
am 2 x2 am 3 x3 ... amn
Здесь
а ij
и
bk —
получившиеся
после
описанных
преобразований новые коэффициенты и свободные члены. Так как
все примененные преобразования являются элементарными, то, по
теореме 1, системы (1) и (2) эквивалентны.
88.
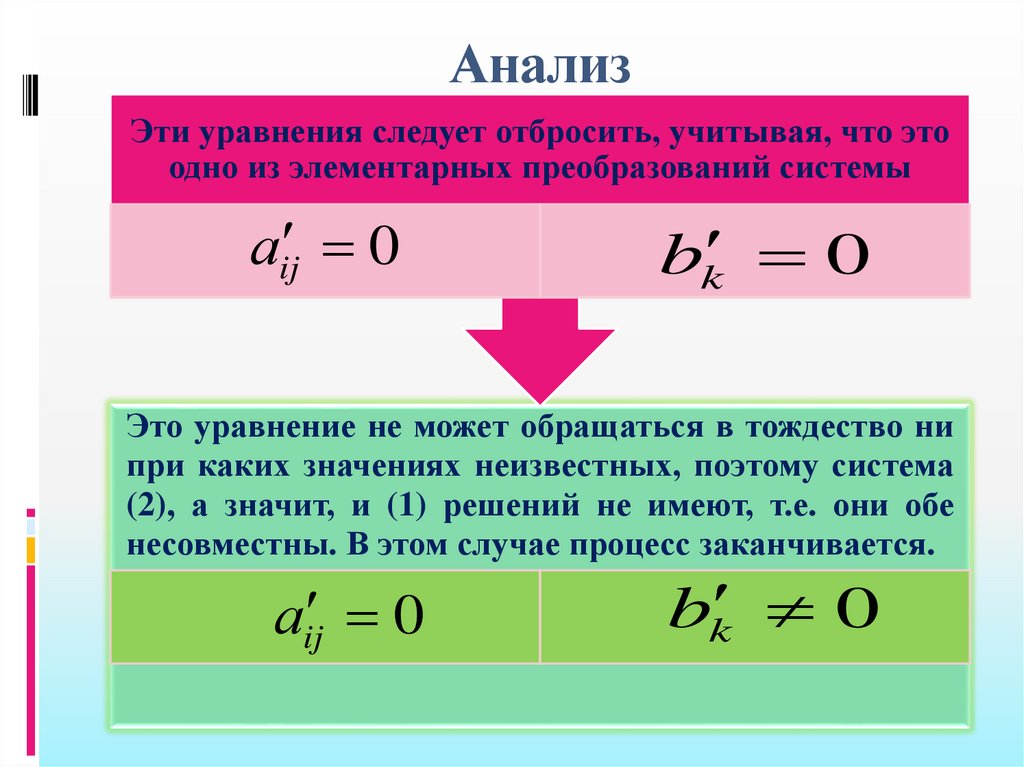
АнализЭти уравнения следует отбросить, учитывая, что это
одно из элементарных преобразований системы
аij 0
bk 0
Это уравнение не может обращаться в тождество ни
при каких значениях неизвестных, поэтому система
(2), а значит, и (1) решений не имеют, т.е. они обе
несовместны. В этом случае процесс заканчивается.
аij 0
bk 0
89.
АнализПроцесс завершится, так как в этом случае
система (1) будет эквивалентна своему
первому уравнению
всеаij 0
всеbk 0
90.
ДОКАЗАТЕЛЬСТВОa11 x1 a12 x2 a13 x3 ... a1n xn b1
a32m 2 a x a x ... a x b
23 3
2n n
2
a 22 2
2222
x2 a33
x3 ... a3 n xn b3 (2)
a32
+
............................................
xn bm
+ am 2 x2 am 3 x3 ... amn
91.
В силу сделанного выше замечания, можем считать, что средикоэффициентов имеются ненулевые; однако может случиться, что
а ij = 0 для всех i= 2,..., n. Тогда следует изменить соответствующим
образом порядок следования неизвестных, мы можем без
ограничения общности считать, что а22 0 .
На следующем этапе преобразования системы (1) первое
уравнение останется неизменным; неизвестное x 2 исключим из
всех уравнений эквивалентной системы (2), начиная с третьего.
Для этого прибавим к обеим частям третьего и каждого из
следующих уравнений обе части второго уравнения, умноженного
соответственно на числа:
am 2
a32
a42
.
, ,…,
a22
a22
a22
По окончании этого этапа преобразования системы следует
сделать такой же анализ, который был проведен после исключения
x1 .
92.
Доказательствоk=n (определенная)
Треугольная
k < n (неопределенная)
Трапецеидальная
a1 n xn b1
a11 x1 a12 x2 ... a1k xk ... a1n xn b1
a11 x1 a12 x2 ...
a
x
...
a
x
b
a22 x2 ... a2 k xk .. a2 n xn b2
22 2
2n n
2
(3)
( 4)
..........
........
..........
..........
.
..................
.....................
( n 1)
( n 1)
( k 1)
( k 1)
ann xn bn
akn xn bk
93.
Решение для системы треугольного типаИз последнего уравнения системы (3) находим вполне
определенное
значение
неизвестного
x n . Подставляя
найденное значение для неизвестного x n в предпоследнее
уравнение системы (3), найдем вполне определенное
значение неизвестного x n 1 . Продолжая процесс нахождения
значений следующих неизвестных, мы найдем, что система
(3), а поэтому и система (1) обладают единственным
решением, т. е. совместны и определены.
94.
Решение для системы трапецеидального типаВыделим k неизвестных x1 , x 2 ,..., x k , оставим слагаемые всех
уравнений системы, содержащие эти неизвестные в левых частях
уравнений, а все остальные перенесем в правые части.
Относительно неизвестных
x1 , x2 ,..., x k
система примет
«треугольный» вид. Из последнего уравнения найдем значение
неизвестного
x k , выраженное через свободные неизвестные
xk 1 ,.., xn . Двигаясь по системе (4) снизу вверх, мы, как и в случае
«треугольного» вида, найдем для неизвестных x k ,.., x1 значения,
выраженные через свободные неизвестные xk 1 ,.., xn . Количество
свободных переменных n-k.
95.
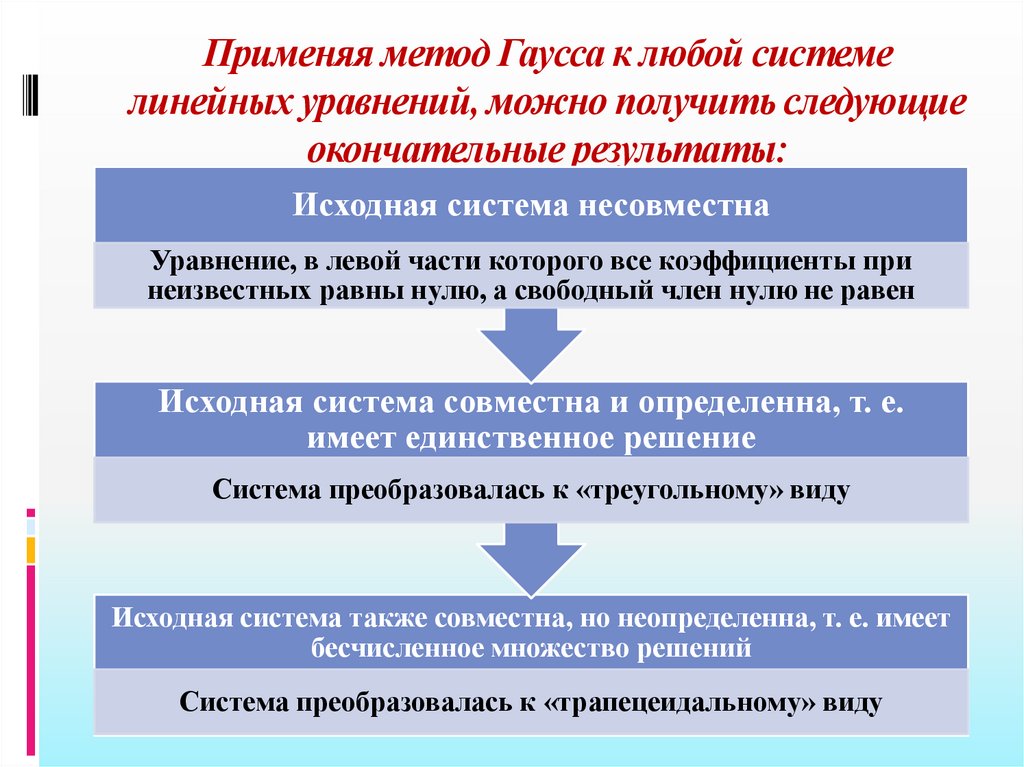
Применяя метод Гаусса к любой системелинейных уравнений, можно получить следующие
окончательные результаты:
Исходная система несовместна
Уравнение, в левой части которого все коэффициенты при
неизвестных равны нулю, а свободный член нулю не равен
Исходная система совместна и определенна, т. е.
имеет единственное решение
Система преобразовалась к «треугольному» виду
Исходная система также совместна, но неопределенна, т. е. имеет
бесчисленное множество решений
Система преобразовалась к «трапецеидальному» виду
96.
ТЕОРЕМА 2.Любую
уравнений
произвольную
с
систему
помощью
линейных
элементарных
преобразований можно привести к равносильной
ей ступенчатого вида.
97.
РАСШИРЕННАЯ МАТРИЦАПри практическом использовании метода Гаусса для
решения
систем
линейных
уравнений
удобно
проводить элементарные преобразования для строк
расширенной матрицы системы:
98.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯI
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII
XIII
XIV
XV
XVII XVIII XIX
XX
XVI
99.
ИНДИВИДУАЛЬНЫЕЗАДАНИЯ
, если
1. Найти
2. Разложить определитель по элементам первой строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
100.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам первого столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
101.
1. Найти –, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам второй строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
102.
1. Найти 3, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам второго столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
103.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам третьей строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
104.
1. Найти,
если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам четвертой строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
105.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам третьего столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
106.
1. Найти 2A+ , еслиИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам четвертого столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
107.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам первой строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
108.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам первого столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
109.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам второй строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
110.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам второго столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
111.
ИНДИВИДУАЛЬНЫЕЗАДАНИЯ
1. Найти
, если
2. Разложить определитель по элементам третьей строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
112.
ИНДИВИДУАЛЬНЫЕЗАДАНИЯ
1. Найти
, если
2. Разложить определитель по элементам третьего столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
113.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ1. Найти -
, если
2. Разложить определитель по элементам четвертой строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
114.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам четвертого столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
115.
ИНДИВИДУАЛЬНЫЕЗАДАНИЯ
1. Найти
, если
2. Разложить определитель по элементам первой строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
116.
1. Найти,
если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам первого столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
117.
ИНДИВИДУАЛЬНЫЕЗАДАНИЯ
1. Найти
, если
2. Разложить определитель по элементам второй строки
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
118.
1. Найти, если
ИНДИВИДУАЛЬНЫЕ
ЗАДАНИЯ
2. Разложить определитель по элементам второго столбца
3. Решить матричное уравнение:
4. Решить систему по правилу Крамера:
5. Решить систему линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). Найти ранг основной и
расширенной матрицы.
119.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯОсновная литература
1.
Бойко А.С. Основы линейной алгебры: учебное пособие /
Пермский филиал МЭСИ, 2011. – 60 с.
2.
Клиот-Дашинский М.И. Алгебра матриц и векторов:
учеб. пособие / М.И. Клиот-Дашинский. – 3. изд. – СПб.: Лань ,
2001 – 156 с.
3.
Курош А.Г. Курс высшей алгебры: учебник / А. Г. Курош.
–18-е изд. –Спб: Лань, 2011. – 431 с.
120.
Дополнительная литература1.
Беллман Р. Введение в теорию матриц / Р. Беллман
– 2-е изд. – М.: Наука,1976. – 351 с.
2.
Блох Э.Л. Основы линейной алгебры и некоторые
ее приложения / Э.Л, Блох, Л.И. Лошинский, В.Я. Турин. –
М.: Высшая школа, 1971. – 256 с.
3.
Варпаховский Ф. Л. Алгебра и теория чисел: учеб.
Пособие / Ф. Л. Варпаховский Г. A. Гальперин, В. Б. Гисин.
– М.: МОГПИ, 1994. – 223 с.
4.
Виноградов
И.
М.
Основы
теории
чисел
/
Виноградов И. М. – 10-е изд., стер. – СПб.:Лань, 2004. – 176
с.
5.
Воеводин, В.В. Линейная алгебра / В.В. Воеводин.
– 2-е изд. – М.: Наука, 1969. – 368 с.
6.
Гантмахер, Ф.Р. Теория матриц / Ф.Р. Гантмахер.
– 4-е изд., доп. – М.: Наука, 1988. – 548 с.
7.
Гельфанд, И.М. Лекции по линейной алгебре/И.М.
Гельфанд. – 3-е изд. – М.: Наука, 1966. – 280с.
8.
Головина, Л.И. Линейная алгебра и некоторые ее
приложения / Л.И.Головина. – М.: Наука, 1971. – 288 с.
9.
Ильин В.А. Позняк Э.Г. Линейная алгебра / В.А.
Ильин, Э.Г. Позняк. – М.: Наука, 1984. – 296с.


























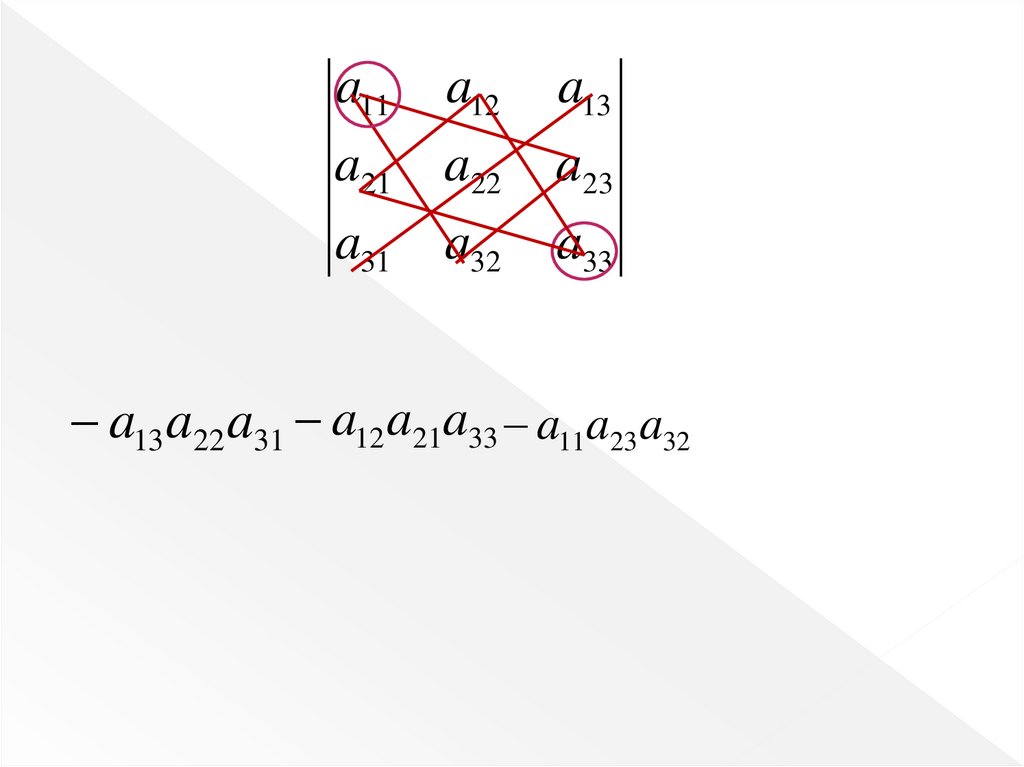

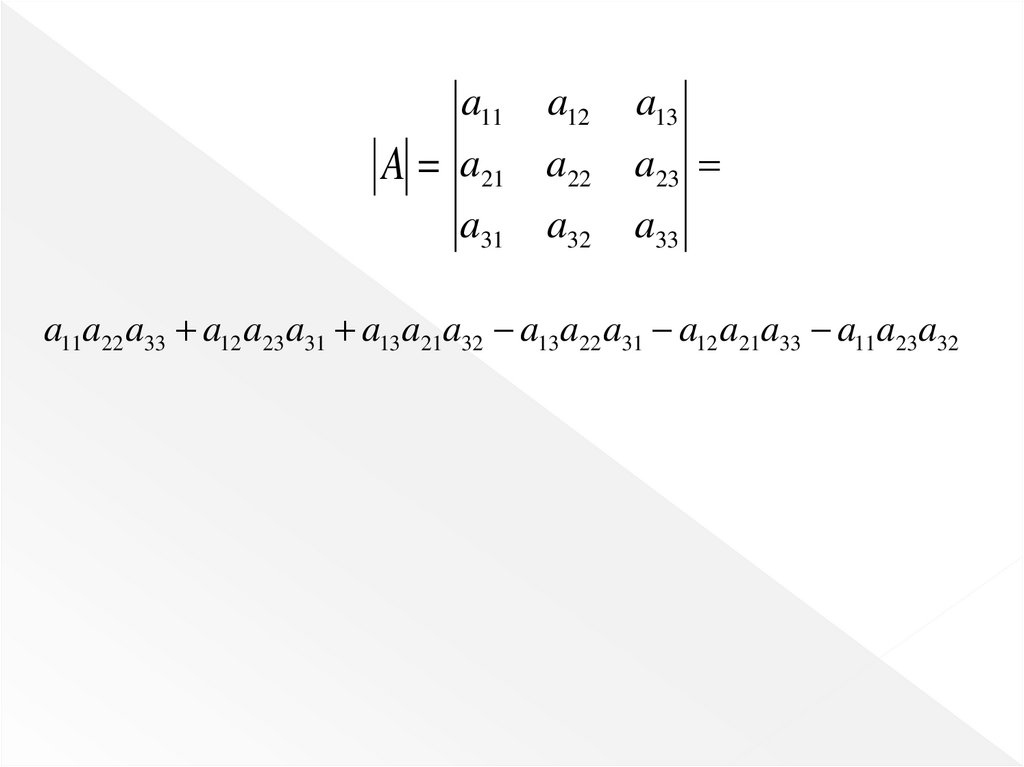
















































































 mathematics
mathematics








