Производная: определение и основные формулы. 11 класс

1. Дистанционный урок «Производная: определение и основные формулы »

алгебра и начала анализа
11 класс

2. Содержание:

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Цели и задачи
Определение производной
Физический смысл производной
Правила дифференцирования
Основные формулы производных
Примеры взятия производных
Производные элементарных функций
Производная сложной функции
Задания для закрепления материала
Задания для самоанализа
Ответы
Домашнее задание
Основная литература

3. Цели и задачи

Цель: познакомиться с одним из важных элементов
математического анализа – производной: ее
определением, физическим смыслом, а также
освоить аппарат нахождения производной различных
функций.
Задачи:
1.
2.
3.
Знать определение производной;
Знать и уметь применять правила
дифференцирования;
Знать и уметь применять формулы для
вычисления производных элементарных
функций.

4.

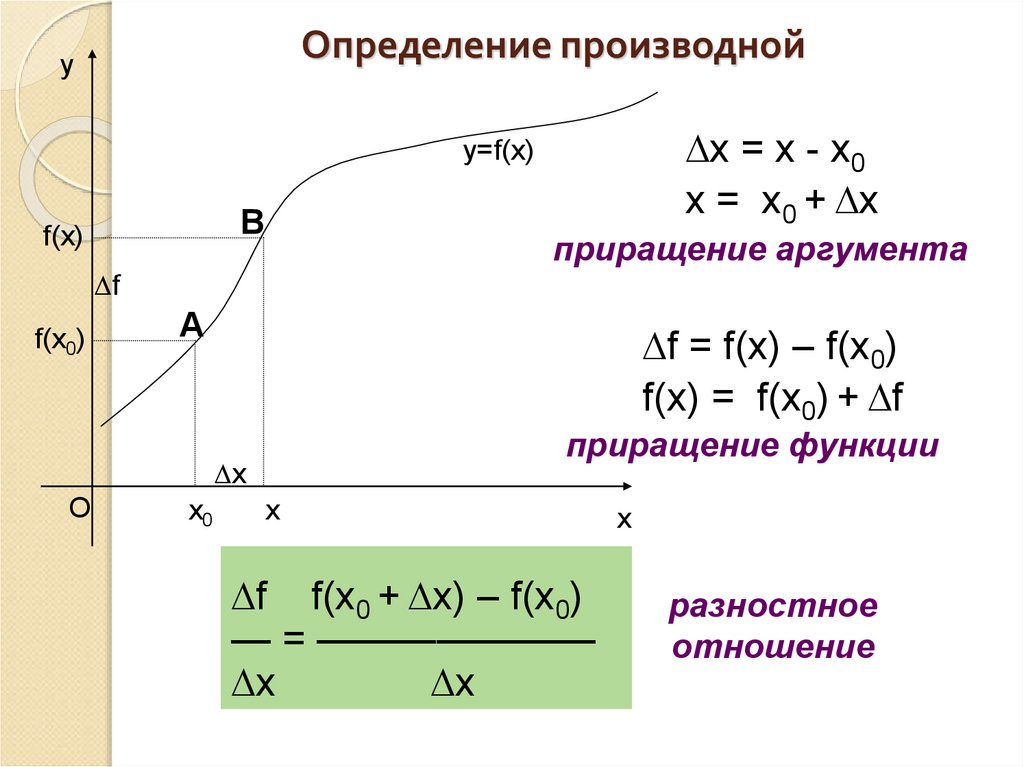
Определение производной
y
x = x - x0
x = x0 + x
y=f(x)
В
f(x)
приращение аргумента
f
f(x0)
А
f = f(x) – f(x0)
f(x) = f(x0) + f
приращение функции
x
O
x0
x
f f(x0 + x) – f(x0)
— = ———————
x
x
x
разностное
отношение

5.

Производной функции f в точке x0
называется число, к которому
стремится разностное отношение
при x 0.
f f(x0 + x) – f(x0)
f´(x0)= lim — = ———————
при x 0 x
x

6.

Физический смысл производной
x
Если тело движется по прямой и за время t
его координата изменяется на x, то
t t(x0 + x) – t(x0) - средняя скорость
Vср( t) = — = ——————— движения тела за t
x
x
Таким образом, физический смысл
производной – это мгновенная скорость

7.

Правила дифференцирования
Если функция y = f(x) имеет производную, то она называется
дифференцируемой; операция нахождения производной
функции называется дифференцированием.
Пусть f(x) , g(x) – дифференцируемые функции, С – постоянная.
(c f ( x)) c f ( x)
( f ( x) g ( x)) f ( x) g ( x)
( f ( x) g ( x)) f ( x) g ( x) f ( x) g ( x)
f ( x) f ( x) g ( x) f ( x) g ( x)
2
g ( x)
g ( x)

8.

Основные формулы производных
x 1
c 0
n 1
x n x
n
x 2
kx b n kx b
n
n 1
1
k
x

9.

Примеры взятия производной
8 0
0
5x 5
5
x 6x
x
8
x 7 x
x
6
7
x5
100
3, 4 x 3, 4
100 x99
100
100 x 101
52 5 32 5 x 3
x x
2
2
1
5
3 4
3
3
4
4 3x 4 x 4 5
x
4 x

10.

Производные элементарных функций
1
ln x
x
log a x
1
x ln a
sin
x
cos x
cos
x
sin x
tgx
1
2
cos x
1
ctgx 2
sin x
x
e e
x
x
a a ln a
x

11.

Производная сложной функции
Пусть f(x) , g(x) – дифференцируемые функции. Тогда:
f g x
f g x g x
Пример:
sin 4x
5
cos 4 x
3x
2
5
2
5
2
sin 4 x 3x 4 x 3x
5
3x 20 x 6 x
2
4

12.

Задания для закрепления материала
Найдите производные, используя образцы.
5
4
4
Образец:(2 x) 2; (5 x 1) 5; (3x ) 3 5 x 15 x
(4 x) ....
(6 x 2) .....
(3 2 x) .....
(2 x 4 ) ..........
(3x6 ) ...........
Образец:y 3e x ; y 3e x
f ( x) e3 x 1; f ( x) e3 x 1 (3x 1) 3e3 x 1
y 5e x ; y ........
y e2 x ; y ..........
y 3e4 x ; y 3(e4 x ) ............... ............
y 0,5e6 x 2 ; y 0,5 (e6 x 2 ) 0,5 e............ (............) .................... ...................

13.

Образец: y 52 x 1;
y 52 x 1 ln 5 (2 x 1) 2ln 5 52 x 1
y 63 2 x ; y ......... ln... (...........) .......................
y 5 23 x ; y .............................................................
Образец:f ( x)
x2 2x ;
f ( x) ( x 2 ) (2 x ) 2 x 2 x ln 2
f ( x) 2 x4 4x ; f ( x) (......) (.....) ..................................................................
y 3x6 52 x 1; y .......................................................................
y 4 x5 2 63 2 x ; y .......................................................................

14. Для каждой из функций, графики которых изображены в верхнем ряду, найдите график ее производной.

15.

Задания для самоанализа
Задание 1. Найдите производные функций:
1. f x 3 x 5
2. f x 4 x 5 x 9 x
2
3
3 x
3. f x
x 3
2
5 7
4. f x 2 3
x
x x
5. f x x 4
1
1
6. f x
2 4x
3x 2 x

16.

Задание 2. Найдите производные функций:
1. f x 3 x 5 x 3
2. f x x 5 x x x
2
3 x
3. f x 3
x
2
2 x 5
4. f x
x 1
5. f x
x 4
3
2
x 2
1 1 2
6. f x 4 x
2 x