Методы решения систем уравнений. Метод подстановки

1.

Методы решения систем уравнений
Метод подстановки
учитель математики
Заикина М.И.
@ МОУ средняя общеобразовательная школа № 20
г. Рыбинск

2.

Является ли пара чисел (3;1) решением уравнения:
Да, так как
3∙3+1=10
верно

3.

Является ли пара чисел (2;3) решением системы уравнений:

4.

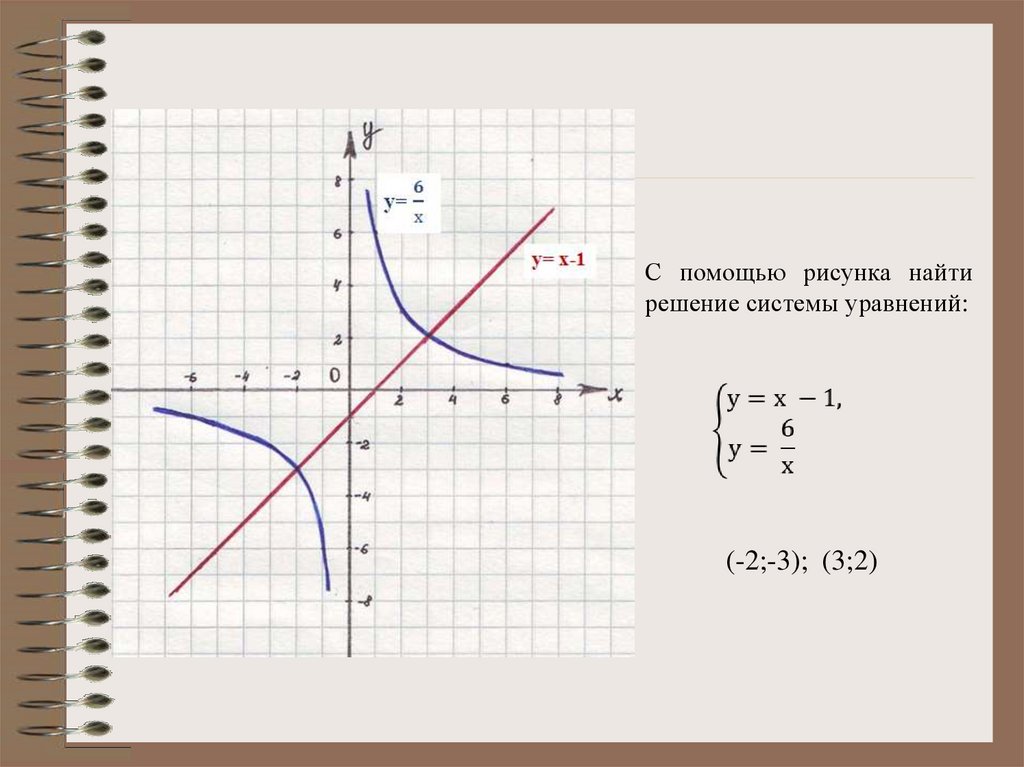
С помощью рисунка найти
решение системы уравнений:
(-2;-3); (3;2)

5.

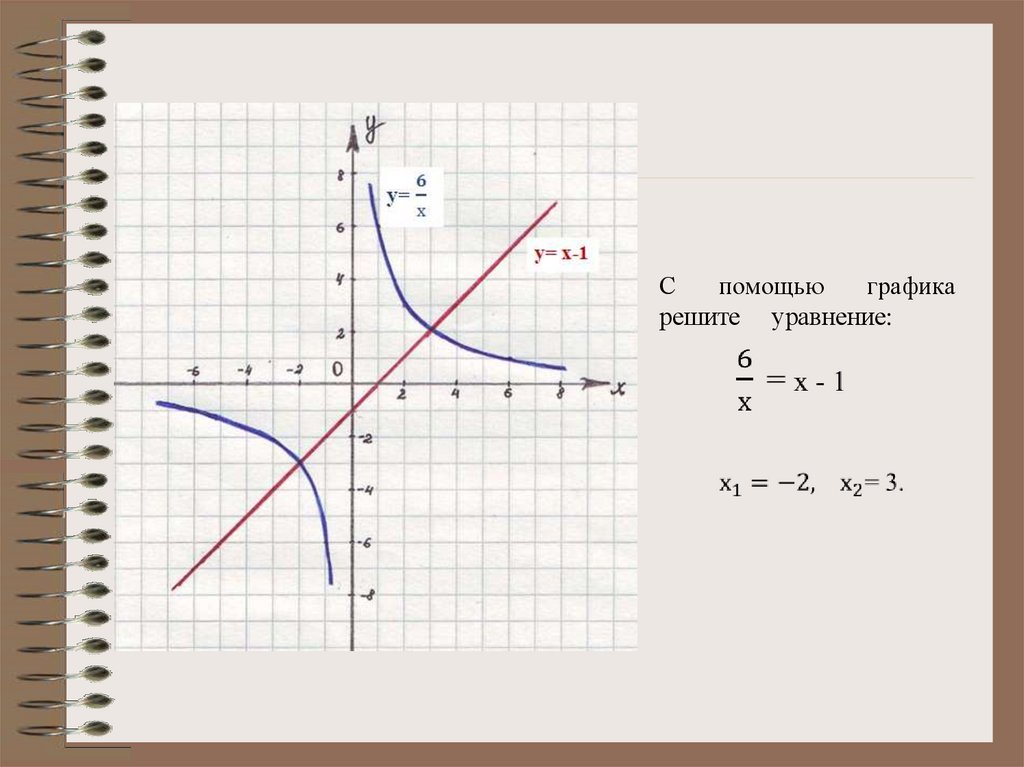
С
помощью
графика
решите уравнение:

6.

Используя данный рисунок, укажите
какая из систем уравнений не имеет
решений:
Ответ: б)

7.

В данных уравнениях выразите переменную
у= 2+х
у
через
х:

8.

Алгоритм использования метода подстановки
при решении системы двух уравнений
с двумя переменными х, у
1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в
другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить каждый из найденных на третьем шаге
корней уравнения поочерёдно вместо х в выражение
у через х , полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые
были найдены соответственно на третьем и
четвёртом шаге.

9.

Решить систему уравнений методом подстановки:
1) Выразим переменную у через х в первом х – у = 1,
уравнении системы:
у = х – 1.
2) Подставим полученное выражение вместо у ху=6,
во второе уравнение системы:
х(х - 1)=6.
3) Решим полученное уравнение:
4)Подставим
поочерёдно
каждое
из Если х= -2, то у = -2-1=-3;
найденных значений переменной х в формулу если х = 3, то у=3-1=2
у = х – 1 и вычислим значение переменной у.
5) Решения заданной системы уравнений:
пары (-2; -3) и (3; 2)
Ответ:
(-2; -3); (3; 2)

10.

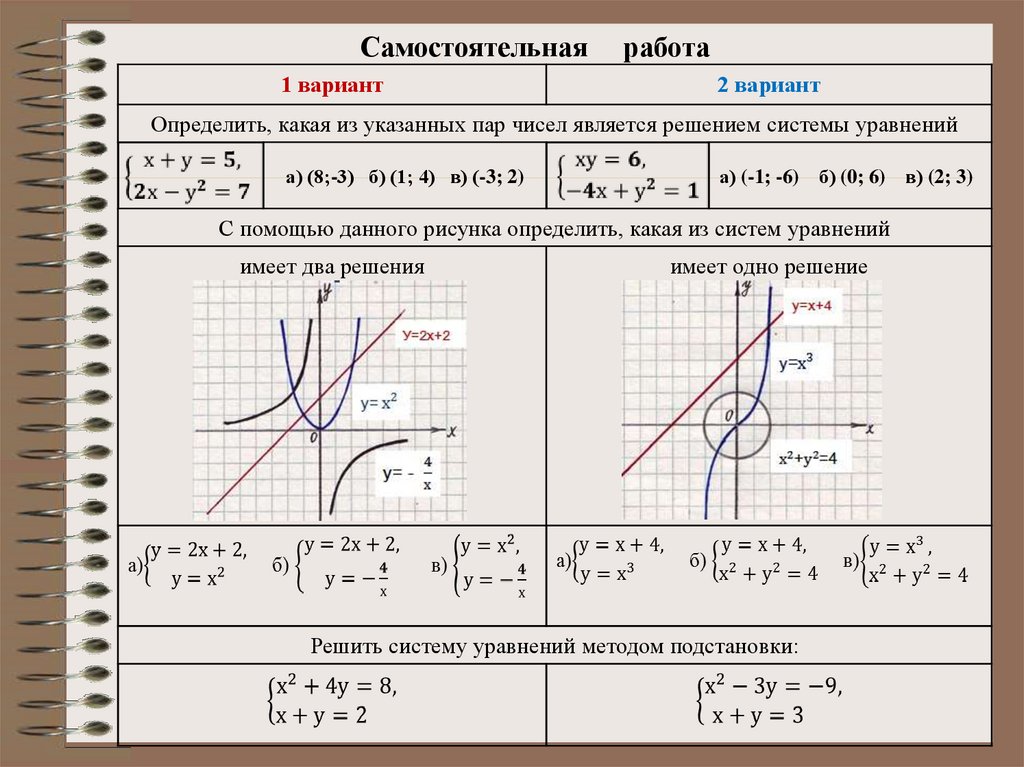
Самостоятельная
1 вариант
работа
2 вариант
Определить, какая из указанных пар чисел является решением системы уравнений
а) (8;-3) б) (1; 4) в) (-3; 2)
а) (-1; -6) б) (0; 6) в) (2; 3)
С помощью данного рисунка определить, какая из систем уравнений
имеет два решения
имеет одно решение
Решить систему уравнений методом подстановки:

11.

Ответы:
1 вариант а), в), в)
2 вариант в), а), а)