Similar presentations:
Арксинус. Решение уравнения sin t = a. 10 класс
1.
Алгебра 10 классУчитель математики
МОУ “Оленовская школа №2
Волновахского района”
Прохоренко Ирина Ивановна
2.
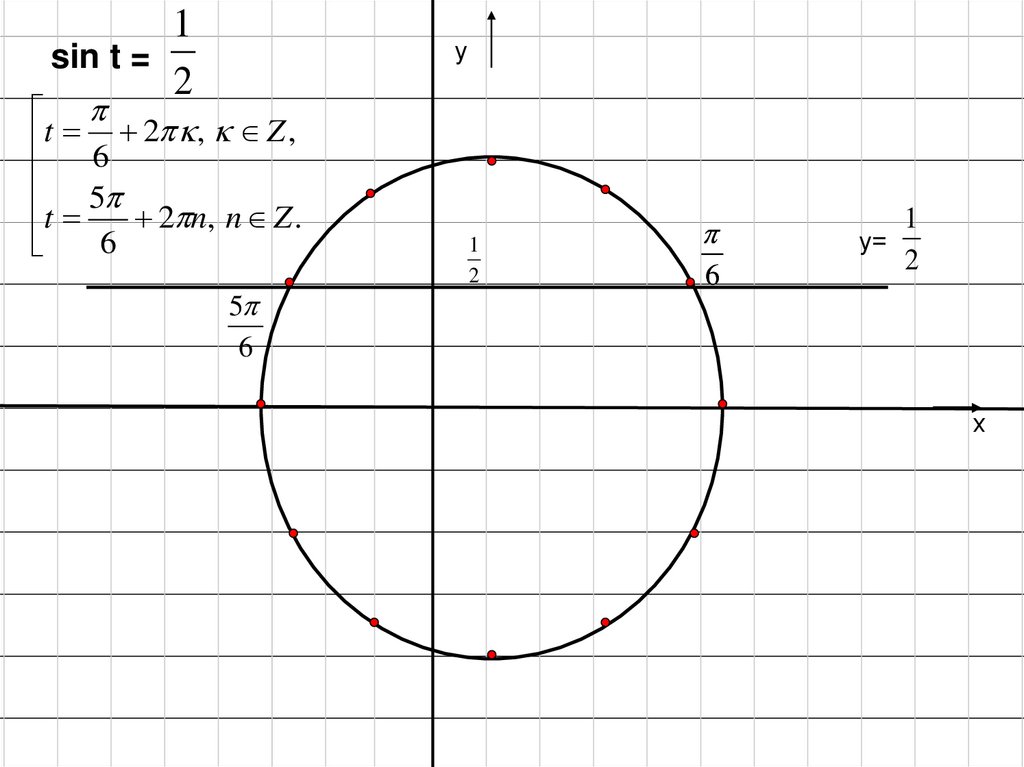
Решить уравнение:1
sin t = .
2
3.
1sin t =
2
у
t 6 2 , Z ,
t 5 2 n, n Z .
6
5
6
1
2
6
1
у=
2
х
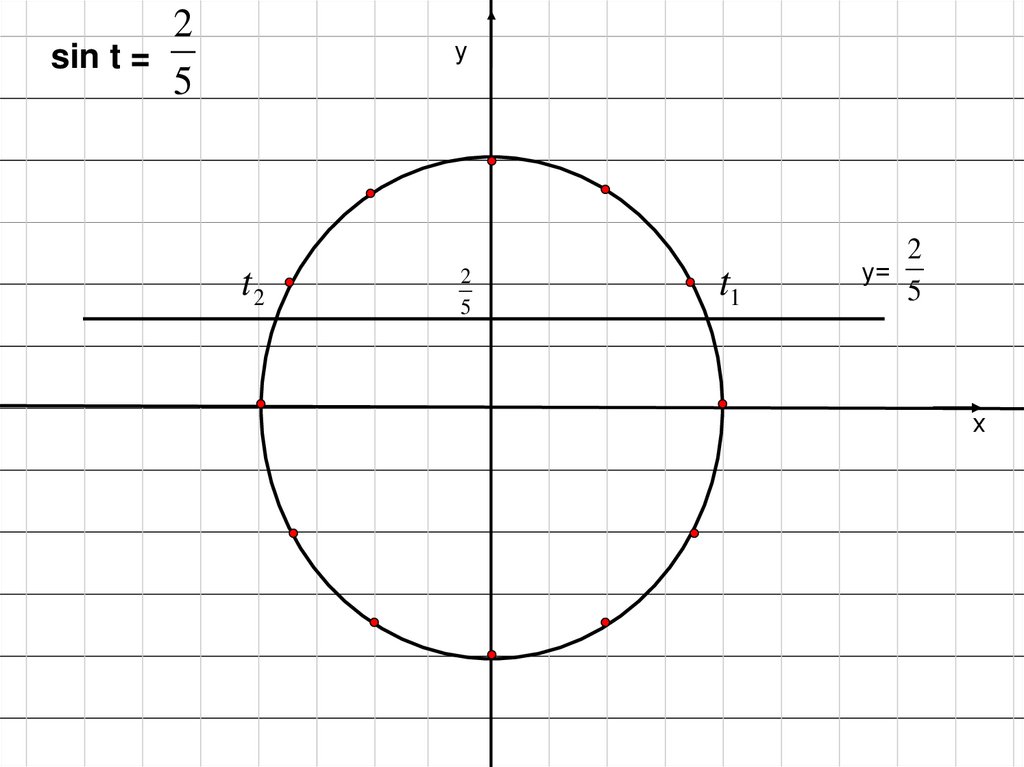
4.
2sin t =
5
у
t2
2
5
t1
2
у=
5
х
5.
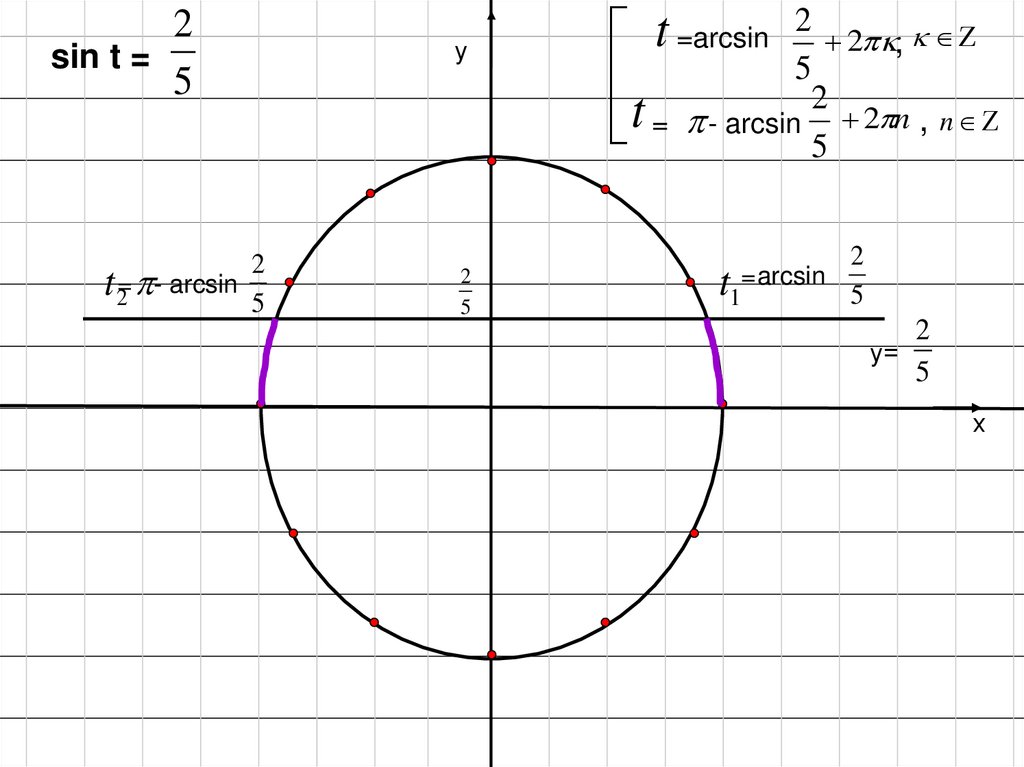
arcsin tЧитается: арксинус t
«arcus» в переводе с латинского значит «дуга»
(сравните со словом «арка»)
С помощью этого символа числа
t1
записываются следующим образом:
2
t1 = arcsin 5
t2
=
2
- arcsin
5
и
t2
6.
2sin t =
5
у
2
t
=arcsin
2 ,
5
t
2
= - arcsin 2 n , n
5
2
t 2= - arcsin 5
2
5
2
t1=arcsin 5
2
у=
5
х
7.
Что же такое2
arcsin
5
?
2
Это – число (длина дуги), синус которого равен
и
5
которое принадлежит первой четверти числовой окружности.
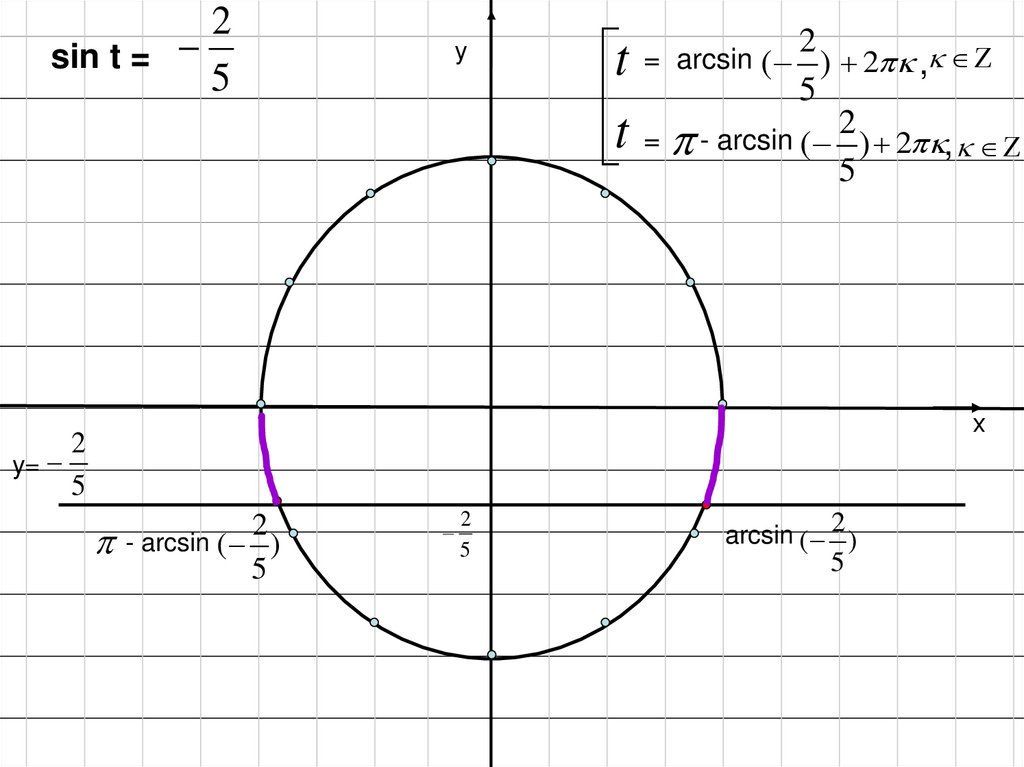
8.
2sin t =
5
у
t
t = - arcsin 2
( ) 2 ,
2
5
= arcsin ( ) 2 ,
5
х
2
y=
5
2
- arcsin ( )
5
2
5
arcsin ( 2 )
5
9.
Что же такое2
arcsin ( )?
5
2
Это – число (длина дуги), синус которого равен и
5
которое принадлежит
четвёртой четверти числовой окружности.
10.
Определение.Если IaI 1, то
sin t a,
arcsin a t
t
.
2
2
11.
Пример 11
arcsin
=
2
6
1
t6 a2 ,
sin
1
arcsin а2 t6
2 t6 2 .
t =?
12.
Пример 22
arcsin ( ) =
4
2
2
(
a, 2 )
sin (t 4 )
2
arcsin ( а2 ) t 4
t
.
4
2
2
t =?
13.
Пример 3arcsin 0 = 0
sin t0 a0,
arcsin а0 0t
t
.
0
2
2
t =?
14.
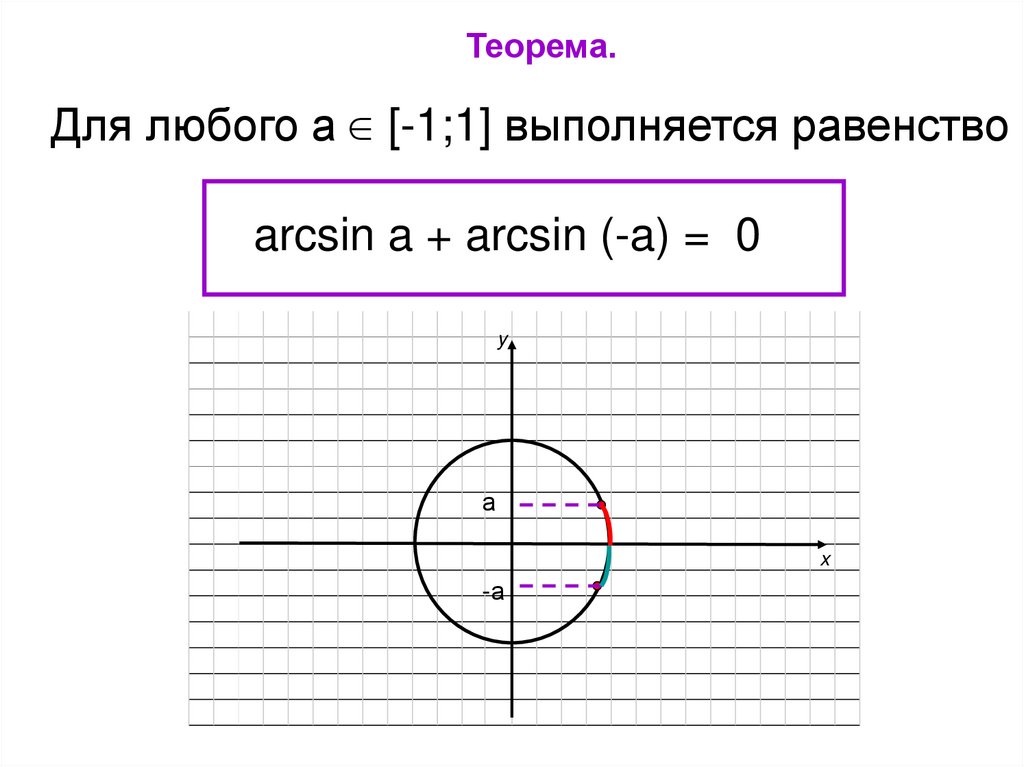
Теорема.Для любого а [-1;1] выполняется равенство
arcsin a + arcsin (-a) = 0
y
а
x
-а
15.
На практике используется:arcsin (-a) = - arcsin a , где 0 а 1
Пример.
2
arcsin ( ) = - arcsin
2
2
= .
2
4
16.
Решение уравнения sint = a.Если IaI 1 , то уравнение sint = a
имеет две серии решений:
t = arcsin a 2 ,
t = - arcsin a 2 +,
17.
Решение уравнения sint = a.Если IaI 1 , то уравнение sint = a
имеет две серии решений:
t = arcsinka 2 ,
t
(
1
)
arcsin
a
k
,
k
Z
t = - arcsin a (2 1) ,
18.
Частные случаи:1) Если sin t = 0, то t =
,
2) Если sin t = 1, то t =
2 ,
2
3) Если sin t = - 1, то t =
2
2 ,
19.
Решение уравненийПример 1.
3
sin t =
2
3
t ( 1) arcsin
k , k Z
2
n
t ( 1)
Ответ: {
n
3
k , k Z
( 1)
n
3
k } , k Z
20.
Пример 2.3
sin t =
2
3
t ( 1) arcsin(
) k , k Z
2
n
t ( 1) ( ) k , k Z
3
n
t ( 1) ( 1) k , k Z
3
n 1
t ( 1)
k , k Z
3
n
Ответ: ( 1)
n 1
3
k / k Z
21.
Пример 3.2
sin t =
7
Решение уравнений
2
t ( 1) arcsin k , k Z
7
n
2
Ответ: ( 1) arcsin k / k Z
7
n
22.
Решение уравненийПример 4.
sin t = 1,2
1,2 < - 1
Ответ: уравнение решения не имеет.
23.
Домашнее задание:§34
№ 586, 589, 590, 591



















 mathematics
mathematics








