Задачи ОГЭ №11, №23. Функции и их графики. Построение графика сложной функции

1. Подготовка к ОГЭ.

Задание №11, №23

2.

Содержание:
№11 Функции и их графики.
№23 Построение графика сложной
функции.

3.

10
9
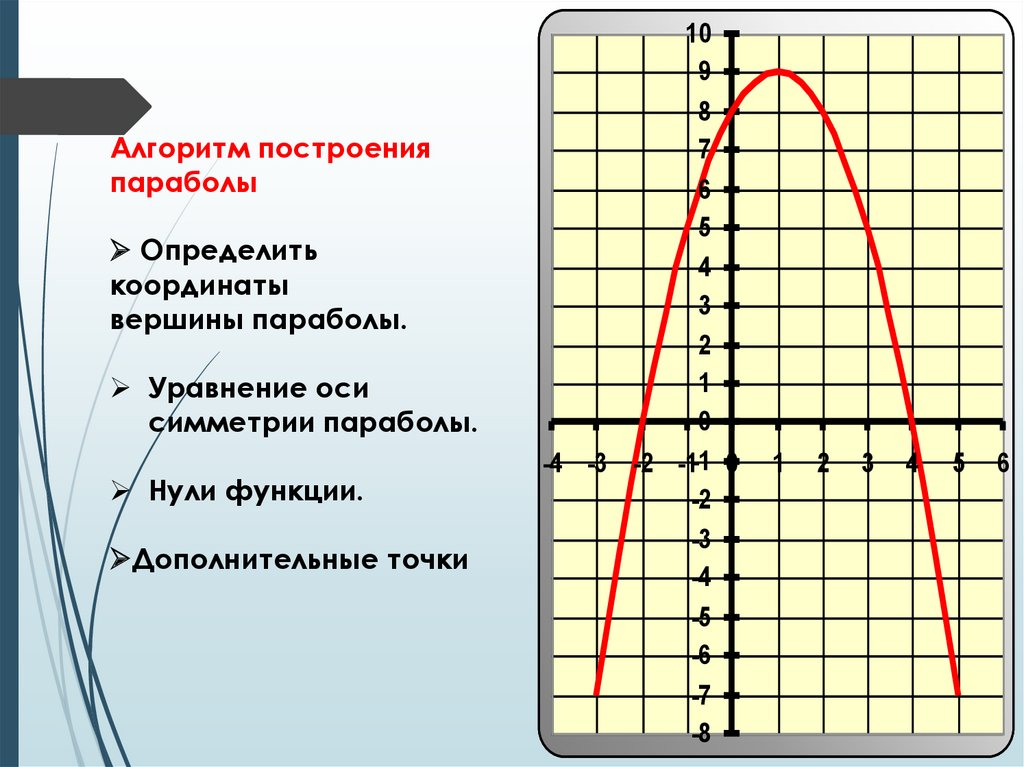
Алгоритм построения
параболы
Определить
координаты
вершины параболы.
Уравнение оси
симметрии параболы.
Нули функции.
Дополнительные точки
8
7
6
5
4
3
2
1
0
-4 -3 -2 -1-1 0
-2
-3
-4
-5
-6
-7
-8
1
2
3
4
5
6

4. Вершину параболы у = ах2+bх+с находим по формуле:

х0
b
; y0 y ( x0 )
2a
Уравнение оси симметрии: х=х0

5. 1.Нахождение значения коэффициента а по графику квадратичной функции у=ax2 +bx+c .

Задания ОГЭ.
1.Нахождение значения
коэффициента а по графику
квадратичной функции
у=ax2 +bx+c .
1) по графику определяем
координаты вершины (m,n)
2) по графику определяем
координаты любой точки А
(х1;у1)
3) подставляем эти значения
в формулу квадратичной
функции, заданной в виде:
У=a(х-m)2+n
4) решаем полученное
уравнение.

6.

Пример. Найдите значение а по графику
функции у=ax2 +bx+c , изображенному на
рисунке.
Решение :
1. Координаты вершины: (m;n)=(-1;1);
2. Координаты любой точки графика:
(х1;у1)=(1;-3);
3. Подставляем в формулу: у=a(х-m)2+n :
-3=а(1-(-1)) 2 +1;
-3=а(1+1) 2 +1;
-3=4а+1;
4а=-4;
а=-1
Ответ : -1

7. 2.Нахождение коэффициента b по графику квадратичной функции у=ax2 +bx+c .

Находим значение
коэффициента a
( смотри выше)
В формулу для абсциссы
вершины параболы
m= -b/2a подставляем
значения m и a
Вычисляем значение
коэффициента b.

8.

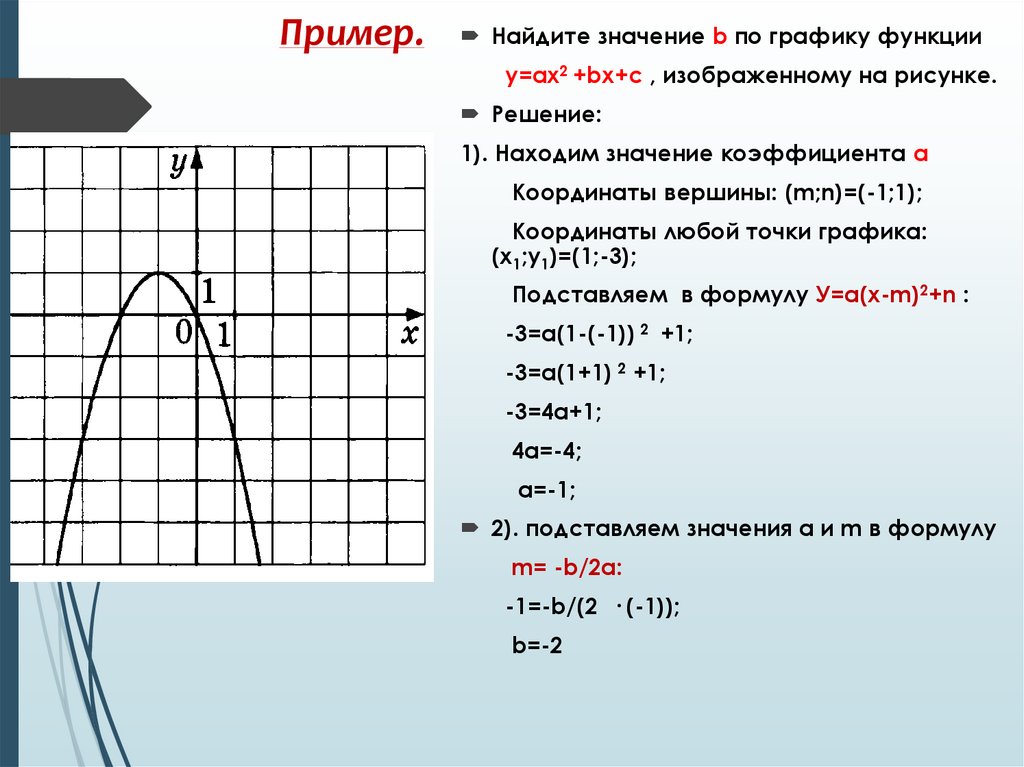
Пример.
Найдите значение b по графику функции
у=ax2 +bx+c , изображенному на рисунке.
Решение:
1). Находим значение коэффициента а
Координаты вершины: (m;n)=(-1;1);
Координаты любой точки графика:
(х1;у1)=(1;-3);
Подставляем в формулу У=a(х-m)2+n :
-3=а(1-(-1)) 2 +1;
-3=а(1+1) 2 +1;
-3=4а+1;
4а=-4;
а=-1;
2). подставляем значения а и m в формулу
m= -b/2a:
-1=-b/(2 · (-1));
b=-2

9. 3.Нахождение коэффициента с по графику квадратичной функции у=ax2 +bx+c ,

Находим ординату точки
пересечения графика с осью Оу,
это значение равно коэффициенту
с, т.е. точка (0;с)-точка пересечения
параболы с осью Оу.
Если по графику невозможно найти
точку пересечения с осью Оу, то
находим коэффициенты a;b
Подставляем найденные значения a,
b , координаты А(х1 ;у1) в уравнение
у=ax2 +bx+c и находим с.

10.

Пример.
Найдите значение с по
графику функции
у=ax2 +bx+c ,
изображенному на
рисунке.
Решение :
1. Ордината точки
пересечения графика с
осью Оу равна 0,
следовательно,
с=0.

11.

Пример.
Найдите значение коэффициентов а,b,с
по графику функции
у=ax2 +bx+c , изображенному на рисунке.
Решение :
1.
Находим значение коэффициента а:
(m;n)=(2;-3)
(х;у)=(3;-1)
-1=а(3-2) 2 –3;
-1=а-3;
а=2;
2.
Находим значение коэффициента b:
2=-b/2· 2
b=-8;
3.
Находим значение с:
у=ax2 +bx+c
-3=2•4-8•2+с
с=5

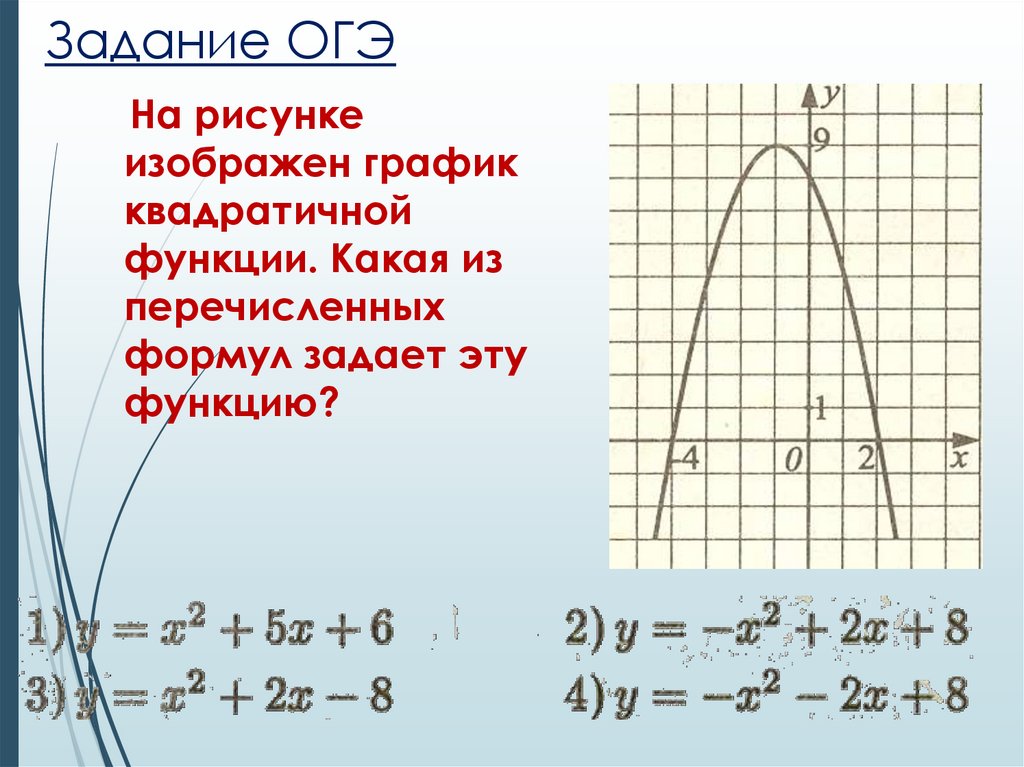
12. Задание ОГЭ

На рисунке
изображен график
квадратичной
функции. Какая из
перечисленных
формул задает эту
функцию?

13.

Тесты ОГЭ №23
x 2
1. Постройте график функции y 1 2
x 2x
и определите, при каких значениях т прямая у = т
не имеет с графиком ни одной общей точки.
Решение.
x 2
y 1 2
x 2x
x 2
x 2
1
1 2
1
1
x 2x
x x 2
x
при условии х 0 и х 2 0 х 0 и х 2.
D y ; 2 2; 0 0; .

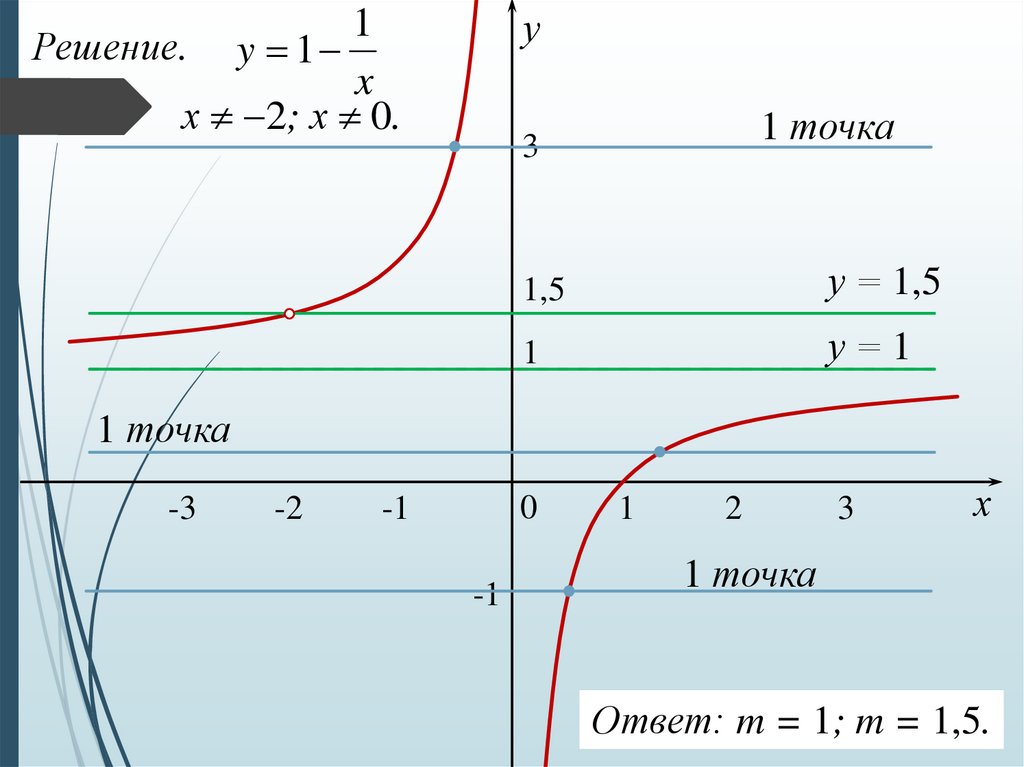
14.

у
1
Решение. y 1
x
х 2; х 0.
1 точка
3
1,5
у = 1,5
1
у=1
1 точка
-3
-2
0
-1
-1
1
2
3
х
1 точка
Ответ: m = 1; m = 1,5.

15.

Спасибо за внимание!