Similar presentations:
Показательная и логарифмическая функция
1.
Показательная илогарифмическая функция
2. Показательная функция. Ее свойства и график.
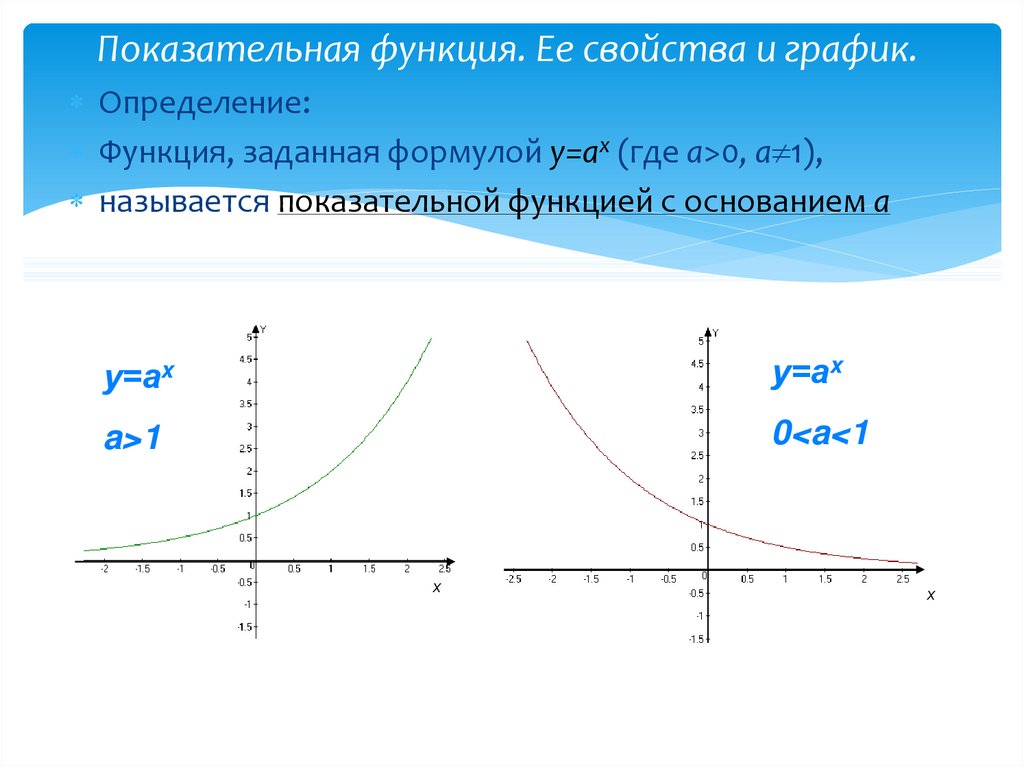
Определение:Функция, заданная формулой у=аx (где а>0, a 1),
называется показательной функцией с основанием а
у=аx
у=аx
a>1
0<a<1
х
х
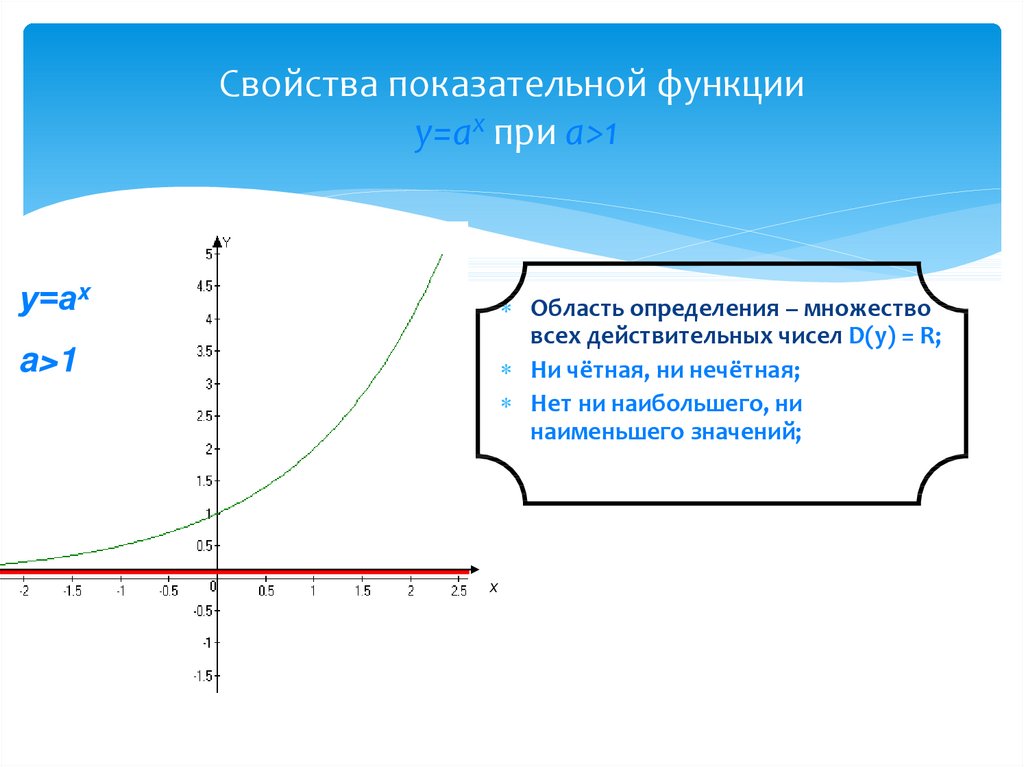
3. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
Область определения – множество
всех действительных чисел D(y) = R;
Ни чётная, ни нечётная;
Нет ни наибольшего, ни
наименьшего значений;
a>1
х
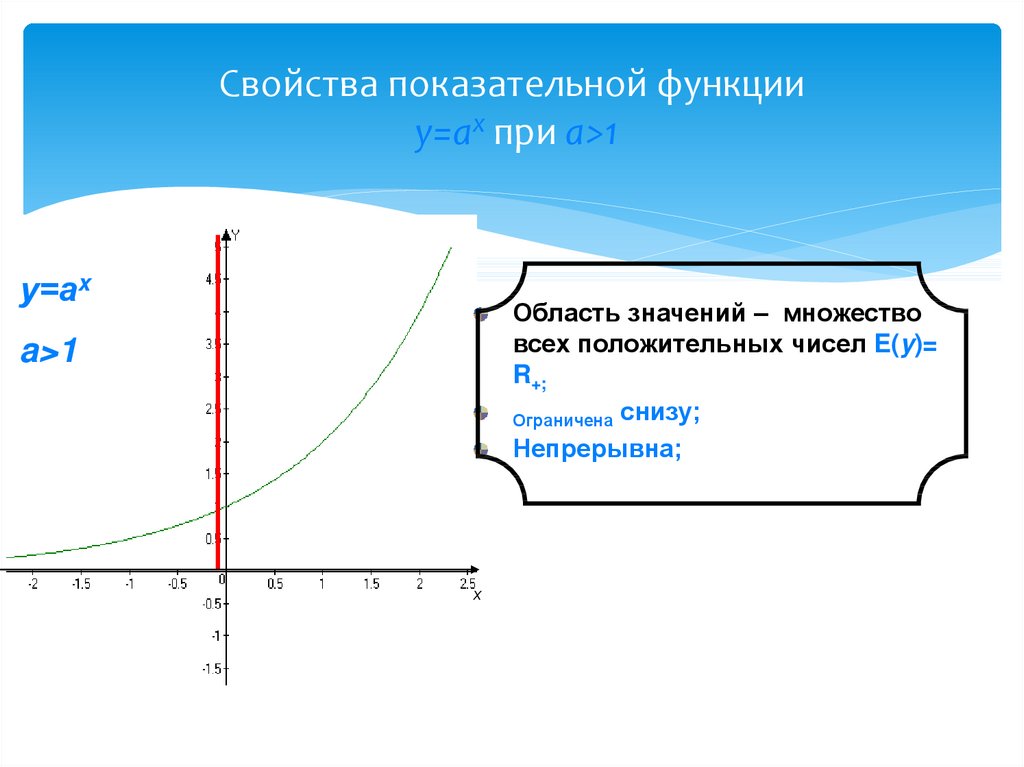
4. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
Область значений – множество
всех положительных чисел E(y)=
R+;
Ограничена снизу;
Непрерывна;
a>1
х
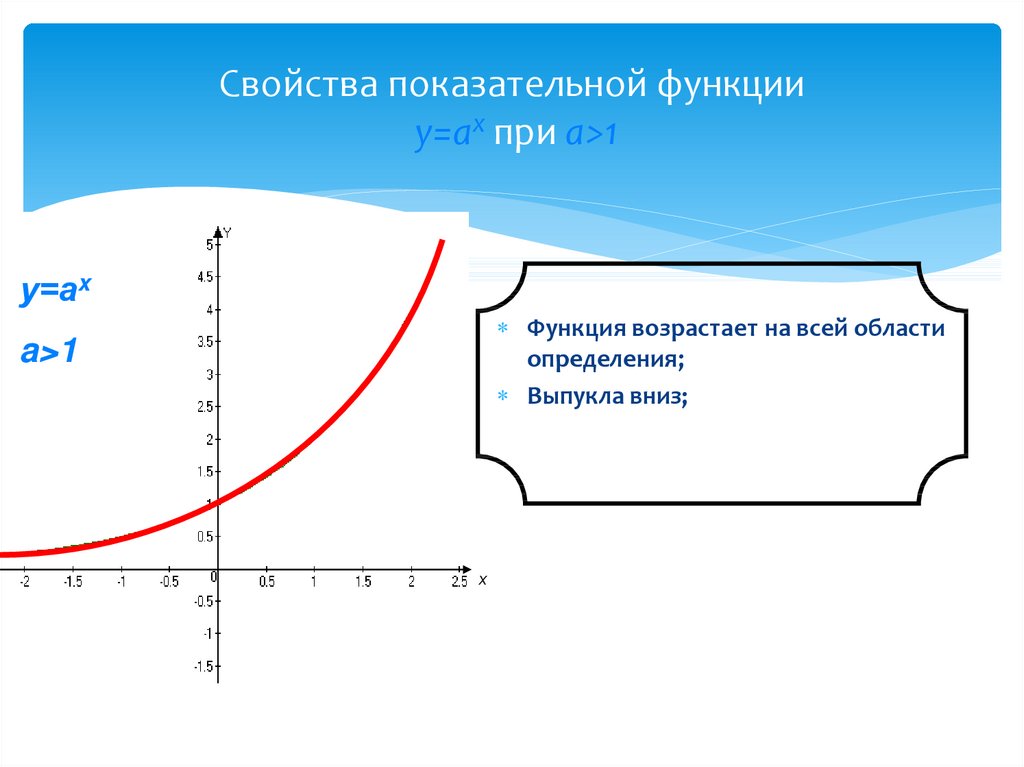
5. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
Функция возрастает на всей области
определения;
Выпукла вниз;
a>1
х
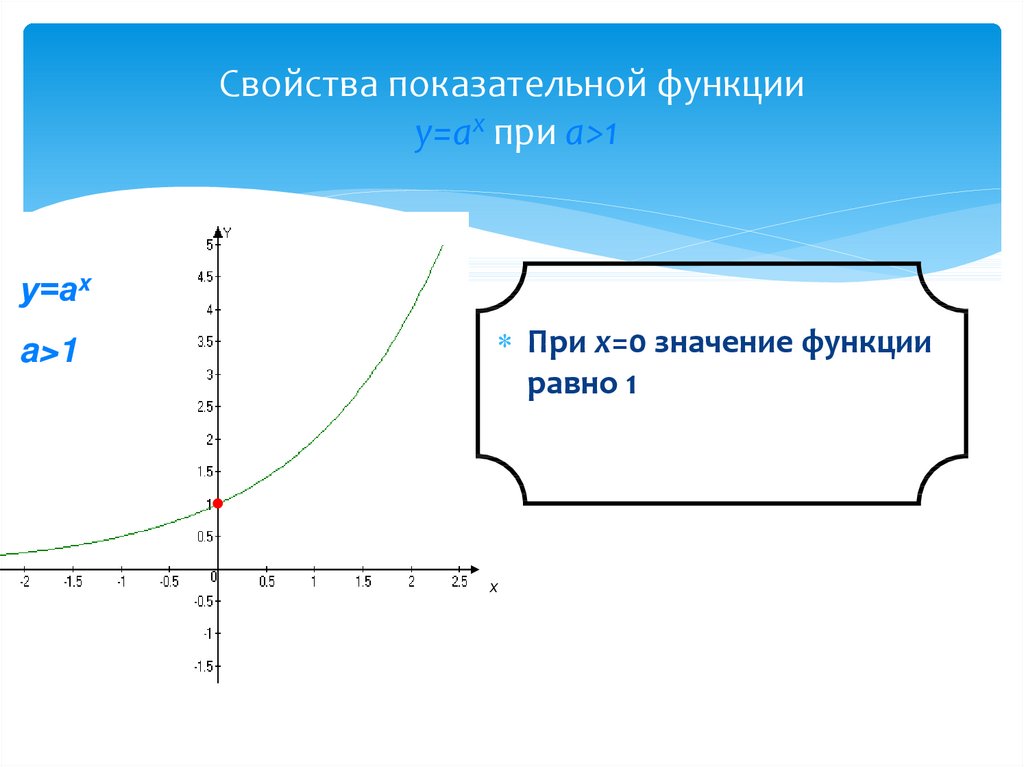
6. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
a>1
При х=0 значение функции
равно 1
х
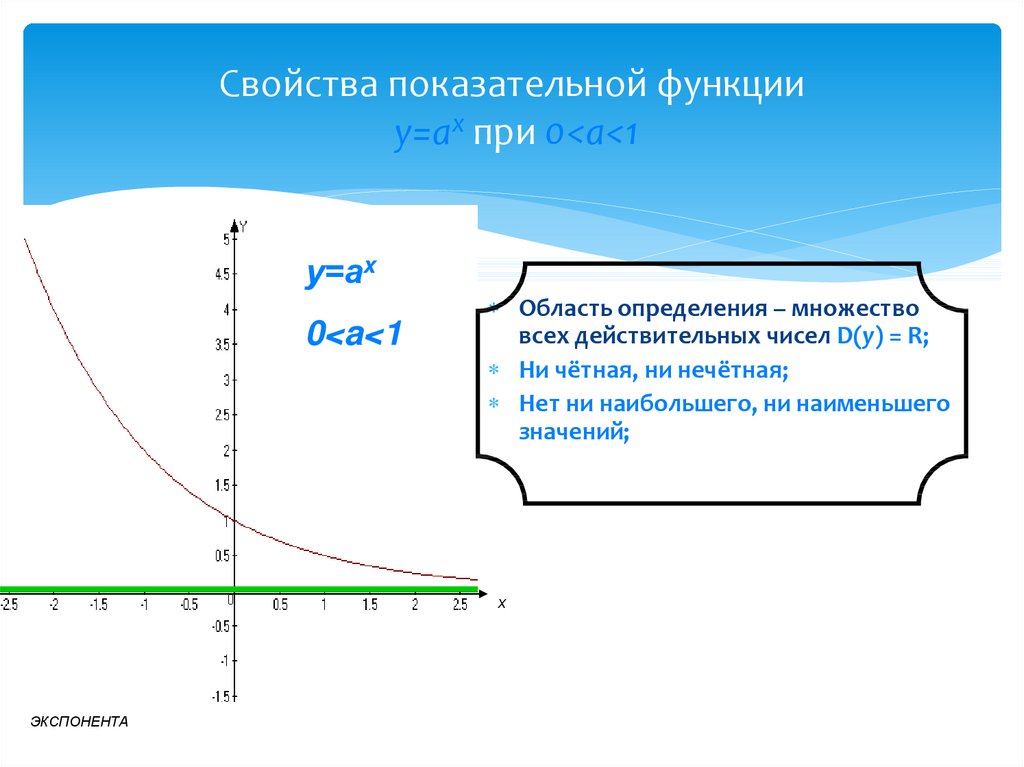
7. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
Область определения – множество
всех действительных чисел D(y) = R;
Ни чётная, ни нечётная;
Нет ни наибольшего, ни наименьшего
значений;
х
ЭКСПОНЕНТА
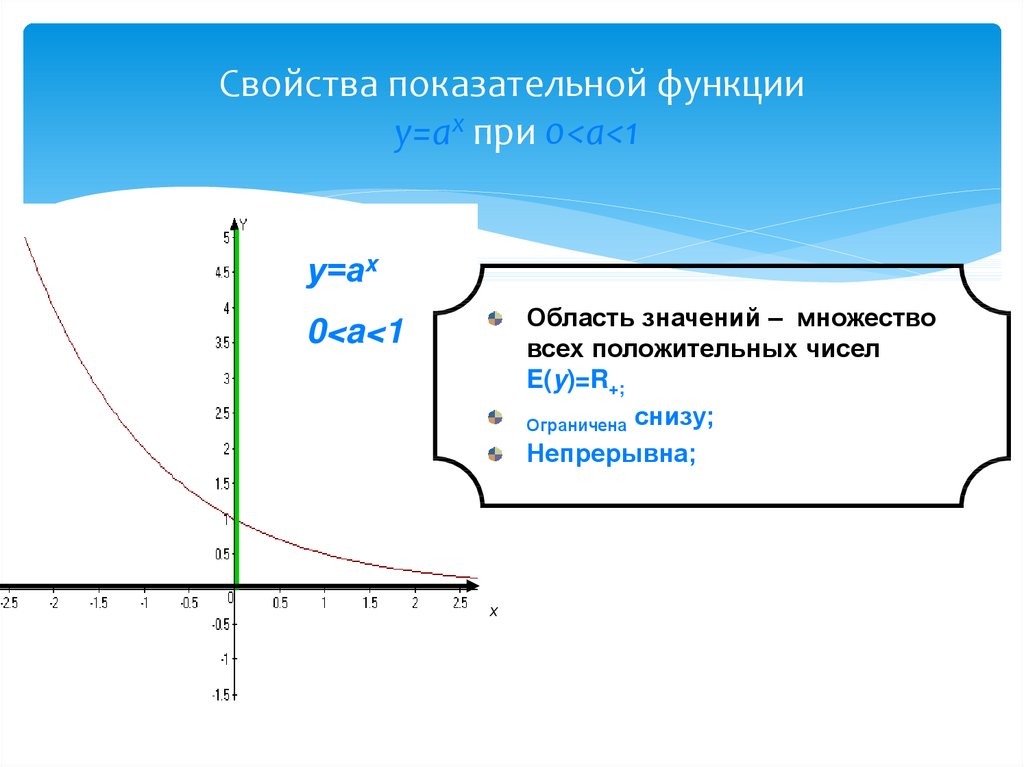
8. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
Область значений – множество
всех положительных чисел
E(y)=R+;
Ограничена снизу;
Непрерывна;
0<a<1
х
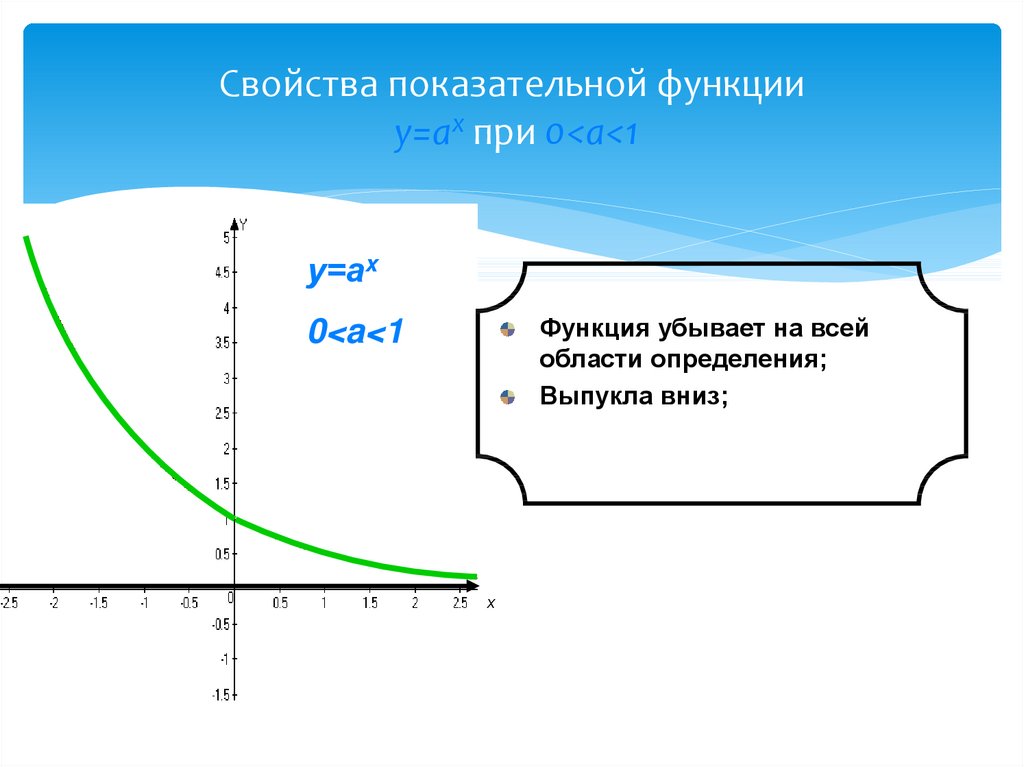
9. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
Функция убывает на всей
области определения;
Выпукла вниз;
0<a<1
х
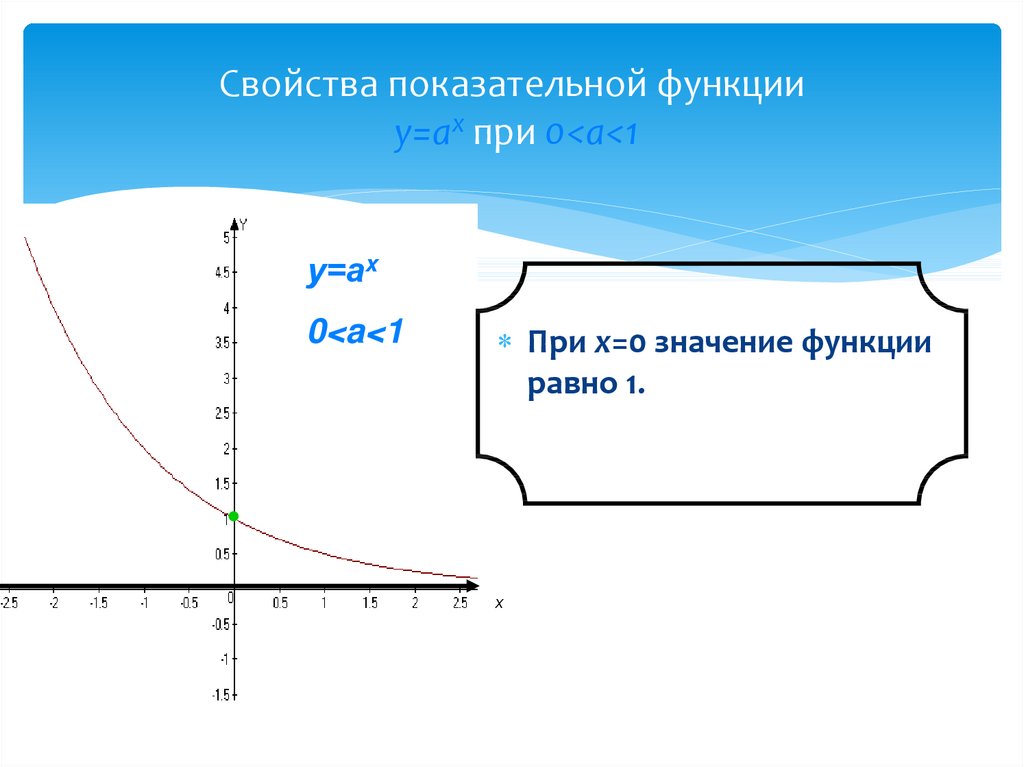
10. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
При х=0 значение функции
равно 1.
х
11. Свойства показательной функции
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.Ноябрь 2007г.
12. Логарифмическая функция
Функцию видаy = logaх, где а ≠ 1, a > 0, х > 0
называют
логарифмической функцией
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
Ноябрь 2007г.
13. Свойства логарифмической функции y = logах, а ≠ 1, a > 0
Свойства логарифмическойфункции y = logах, а ≠ 1, a > 0
6.
Не имеет ни наибольшего, ни наименьшего значений
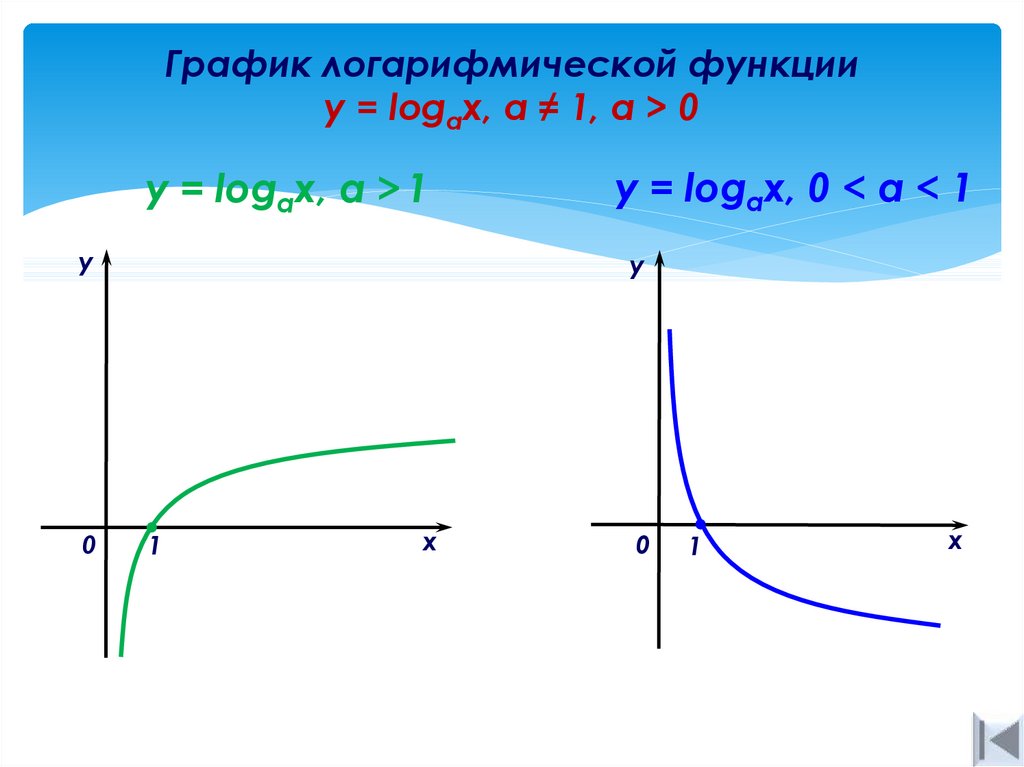
14. График логарифмической функции y = logах, а ≠ 1, a > 0
График логарифмической функцииy = logах, а ≠ 1, a > 0
y = logaх, а > 1
у
0
y = logах, 0 < а < 1
у
1
х
0
1
х
15. Графики логарифмической функции y = logах, а ≠ 1, a > 0
Графики логарифмической функцииy = logах, а ≠ 1, a > 0
16. Логарифмическая функция
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.Ноябрь 2007г.






 mathematics
mathematics








