Similar presentations:
Показательная функция, ее свойства и применение
1. Показательная функция, ее свойства и применение.
Организация итогового повторенияпо алгебре и началам анализа
в 11 классе
Лысенко Л.М.
2.
Ноябрь 2007г.Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
3. Показательная функция, ее свойства и применение.
Степень с рациональным показателем.Показательная функция.
Показательные уравнения.
Показательные неравенства.
Дополнительный справочный
материал.
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
4.
Как алгебраисты вместо АА, ААА, … пишут А2, А3, …так я вместо
1 1 1
, 2 , 3 пишу а-1, а-2, а-3, …
а а а
Ньютон И.
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
5. Свойства степени с рациональным показателем
Если а>0, то:1. a m a n a m n ;
n
2. a : a
m
7.
8.
9. 1n 1;
a n m ;
п
п п
(
ав
)
а
в ;
3.
n
n
n
a
b
a
b
;
4.
n
5. a
b
n
10.
0 n 0, где
11. Если
1
a n ;
a
Ноябрь 2007г.
n 0;
r
r
r Q,0 a b, то a b
n
a
, где b 0
b
n
6.
a1 a;
a 0 1;
при r>0 и
a r br
12. Если r , s Q, r s, то
При a>1 и
ar as
при r<0;
ar as
при 0<a<1.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
6.
Л. Эйлерматематик, механик,
физик и астроном
Некоторые наиболее
часто встречающиеся
виды
трансцендентных
функций, прежде
всего показательные,
открывают доступ ко
многим
исследованиям.
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
7. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
«Деятельность учителя неотделима от деятельностиучащихся… Она должна состоять из трех основных
этапов:
мотивационного,
операционнопознавательного и рефлексивно-оценочного».
Фридман Л.М.
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
СВОЙСТВА И ГРАФИК
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
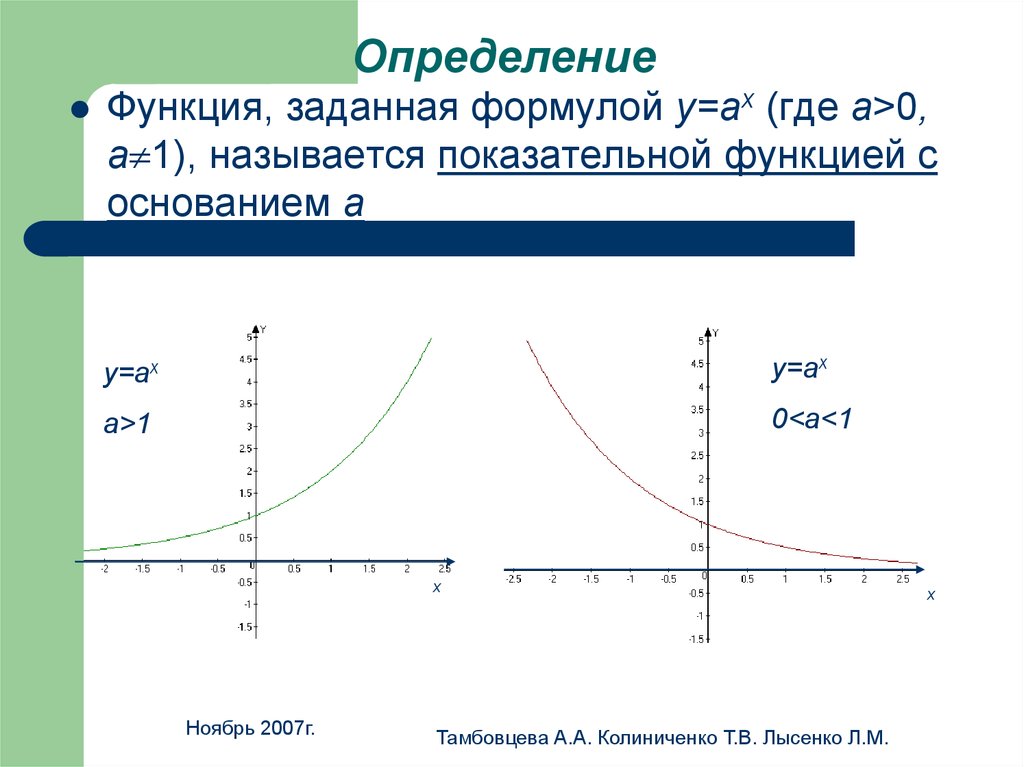
8. Определение
Функция, заданная формулой у=аx (где а>0,a 1), называется показательной функцией с
основанием а
у=аx
у=аx
a>1
0<a<1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
х
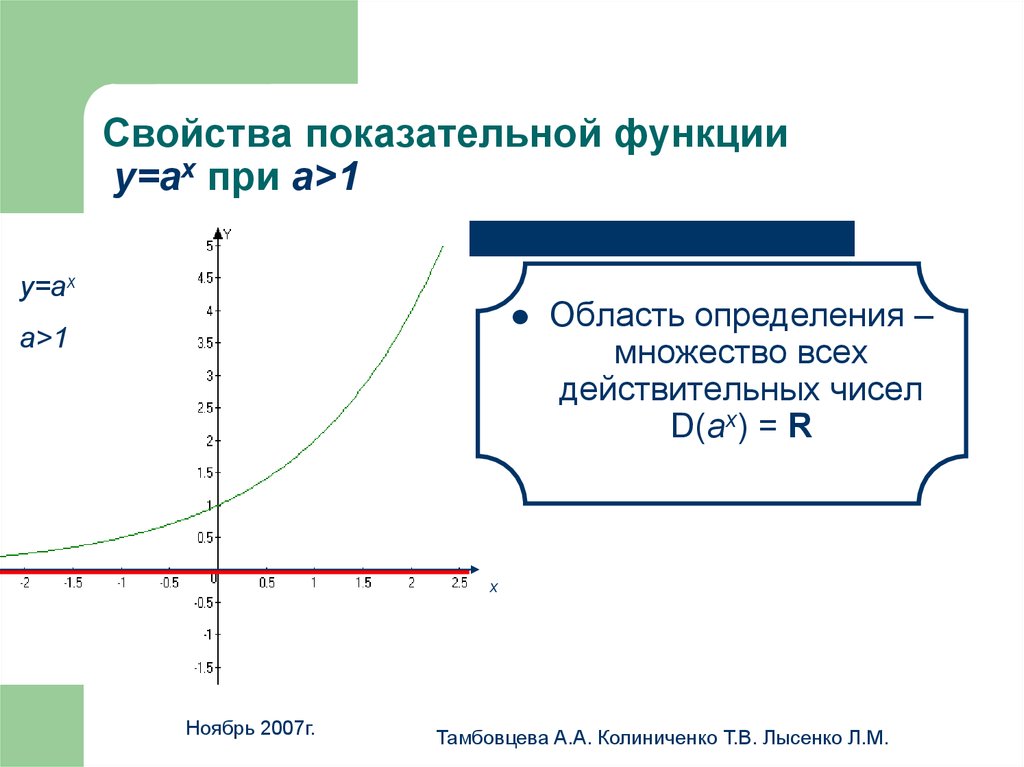
9. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
a>1
Область определения –
множество всех
действительных чисел
D(аx) = R
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
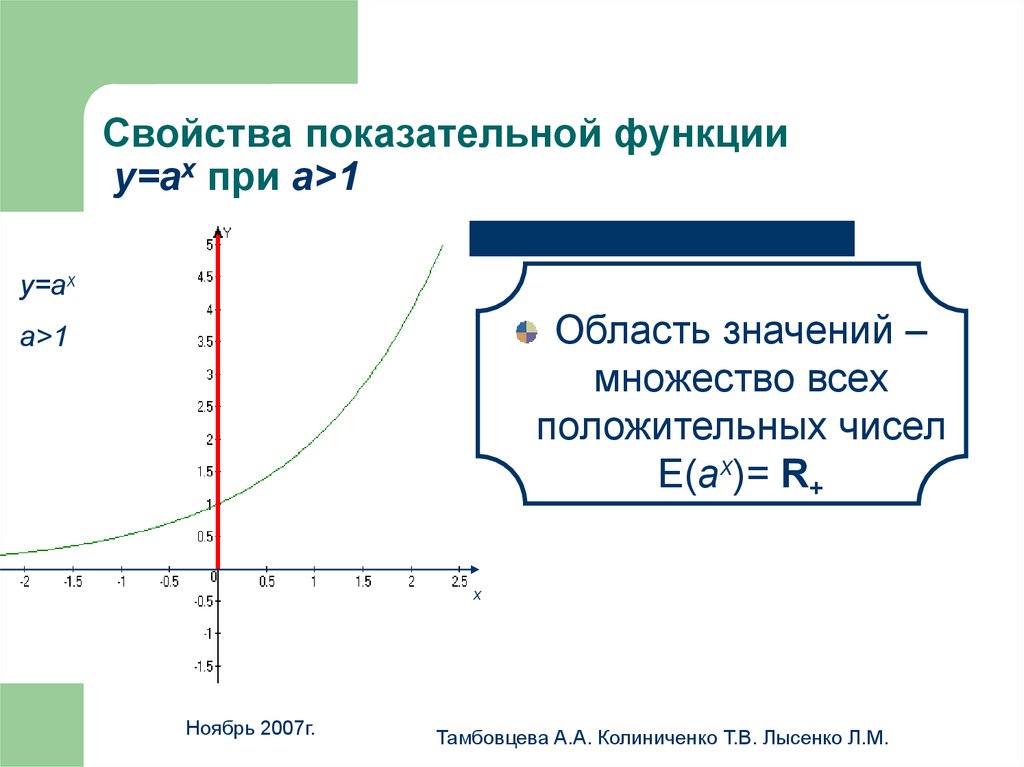
10. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
Область значений –
множество всех
положительных чисел
E(аx)= R+
a>1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
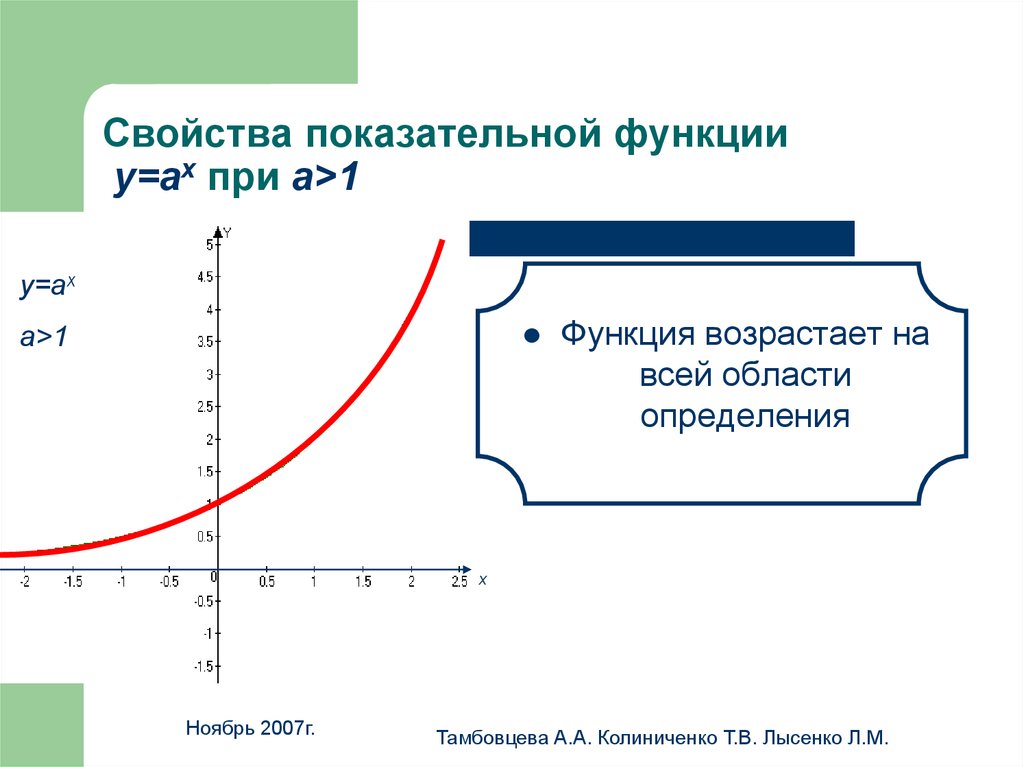
11. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
a>1
Функция возрастает на
всей области
определения
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
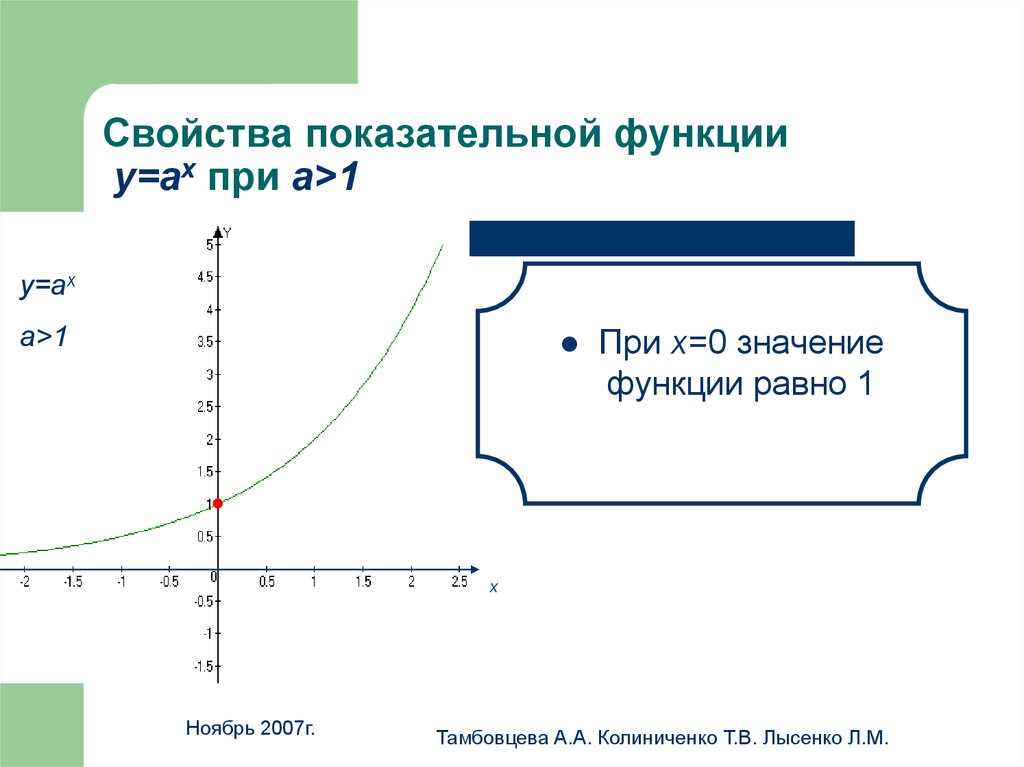
12. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
a>1
При х=0 значение
функции равно 1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
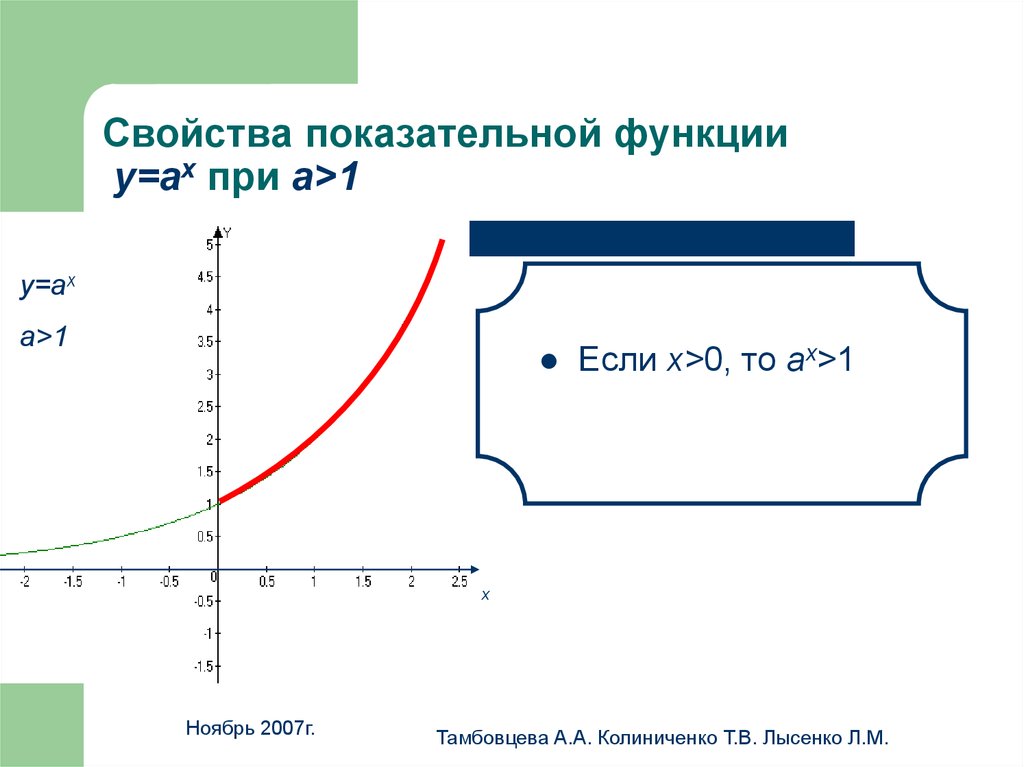
13. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
a>1
Если х>0, то аx>1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
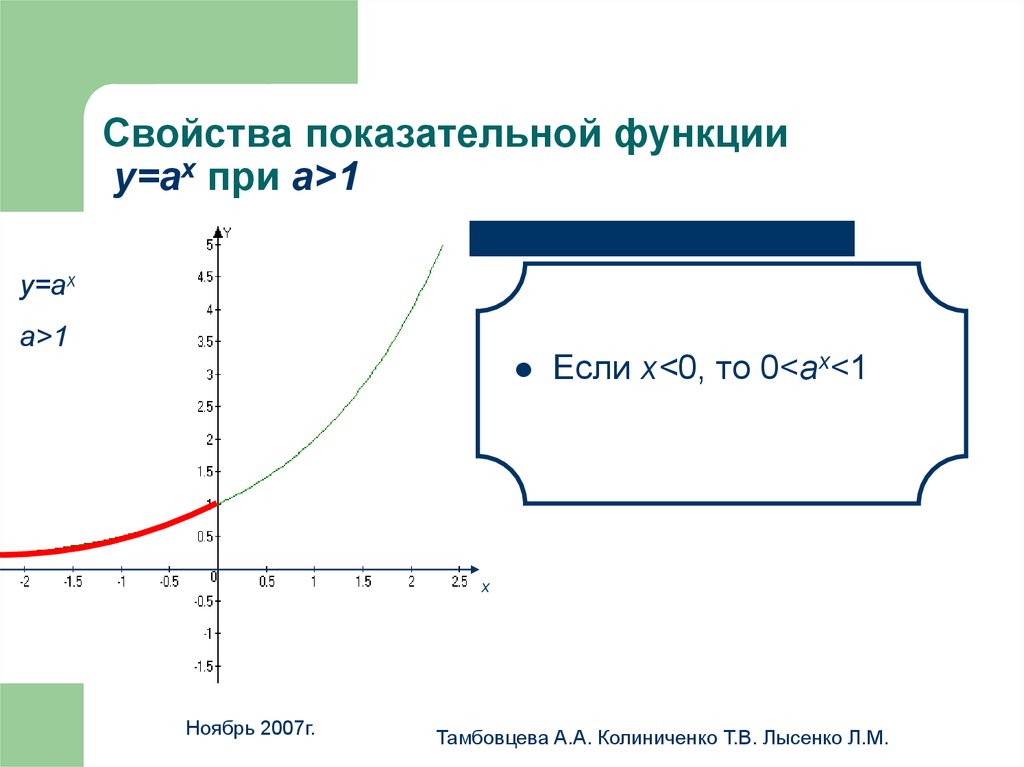
14. Свойства показательной функции у=аx при а>1
Свойства показательной функцииу=аx при а>1
у=аx
a>1
Если х<0, то 0<аx<1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
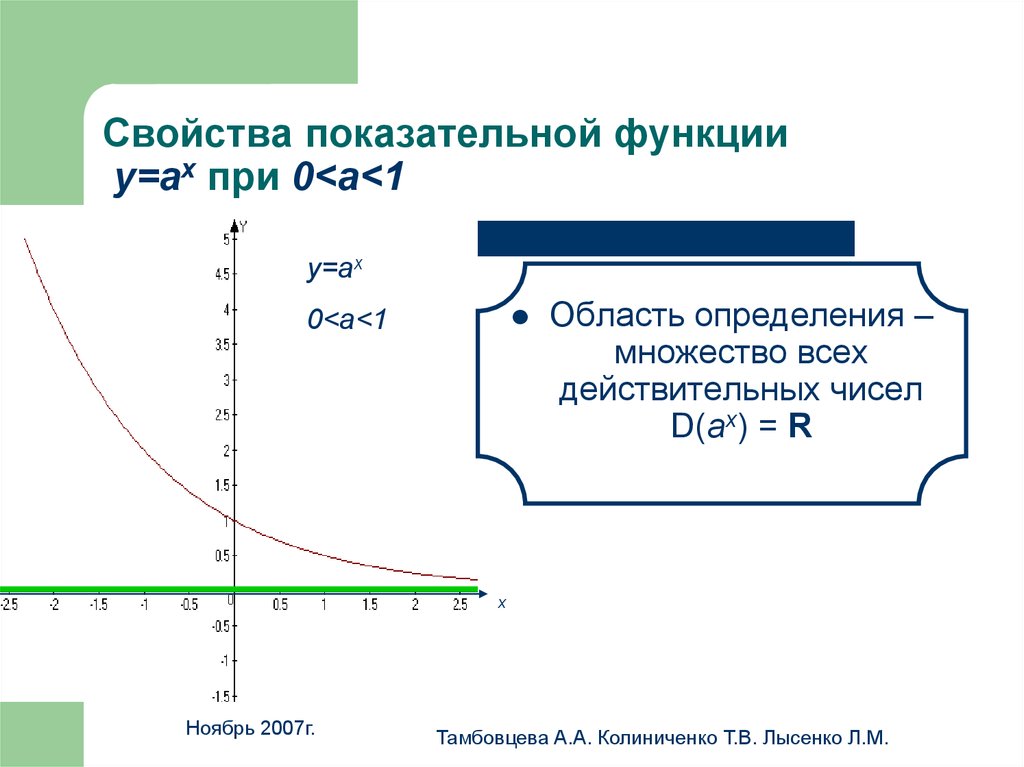
15. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
Область определения –
множество всех
действительных чисел
D(аx) = R
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
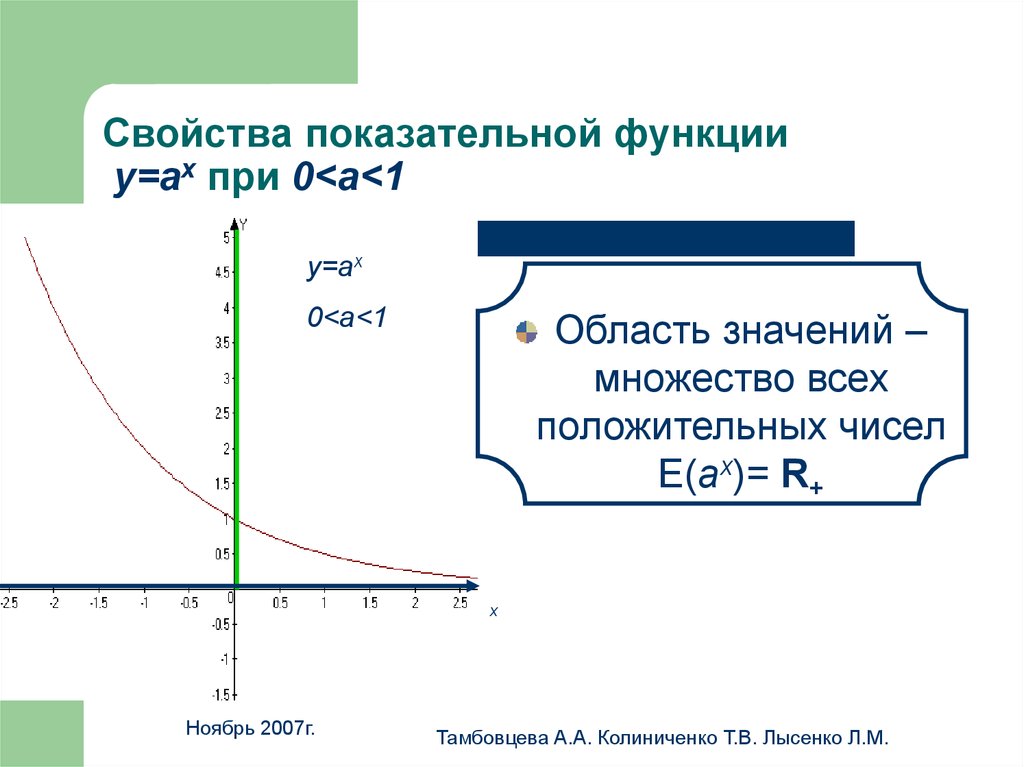
16. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
Область значений –
множество всех
положительных чисел
E(аx)= R+
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
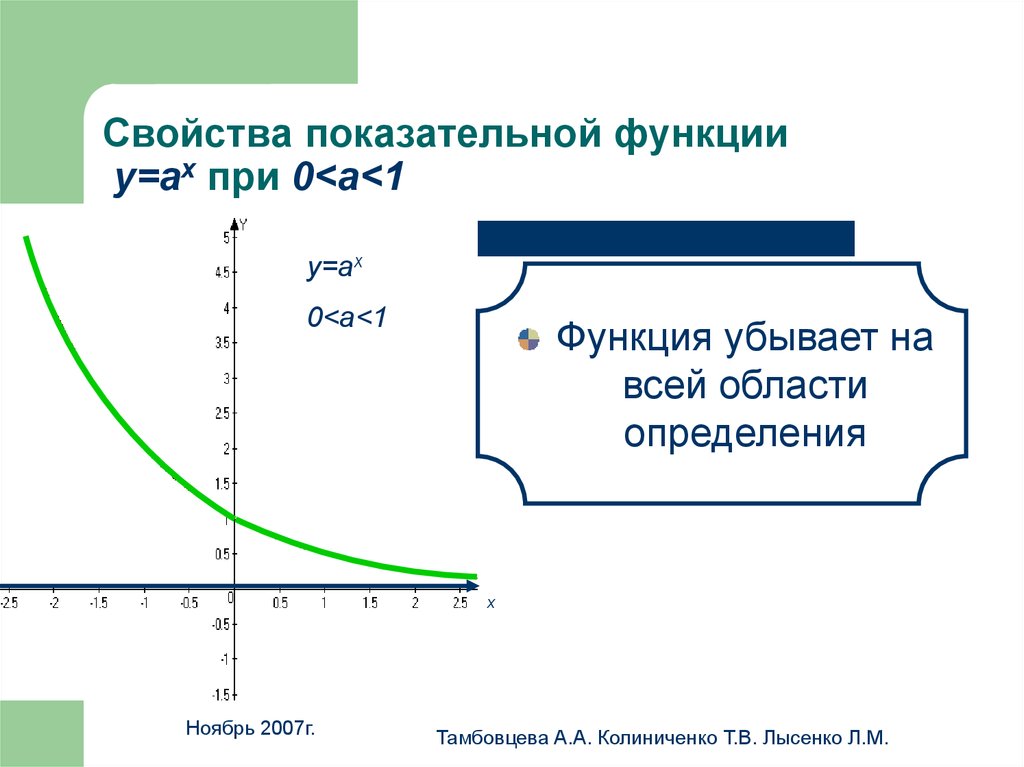
17. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
Функция убывает на
всей области
определения
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
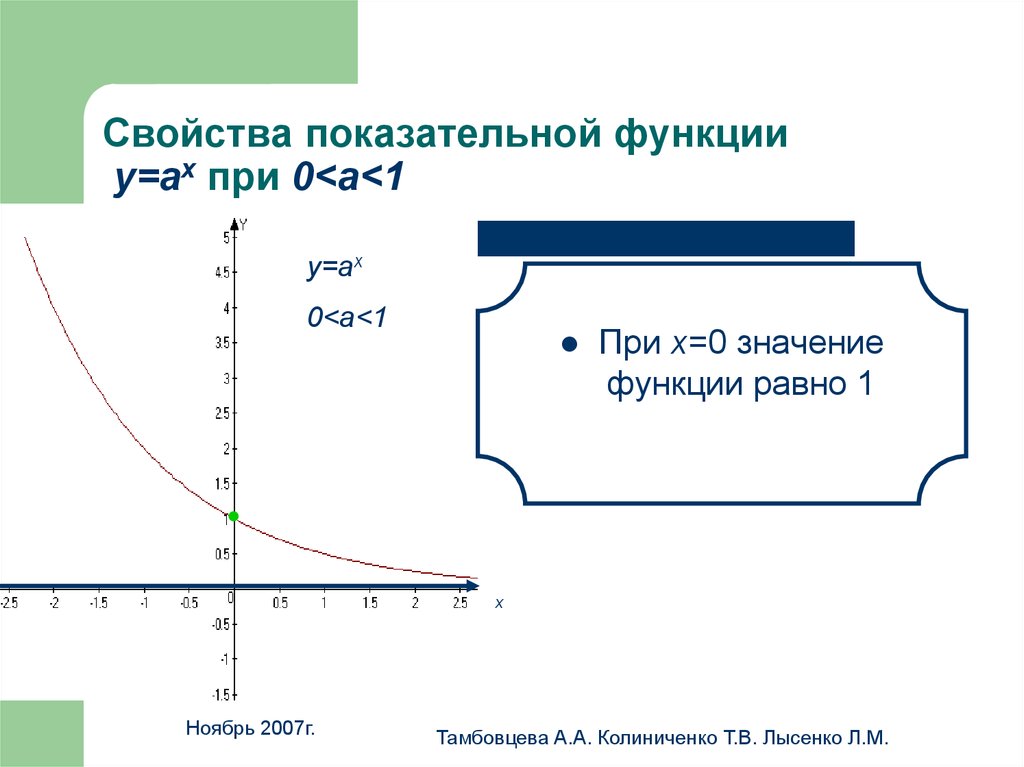
18. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
При х=0 значение
функции равно 1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
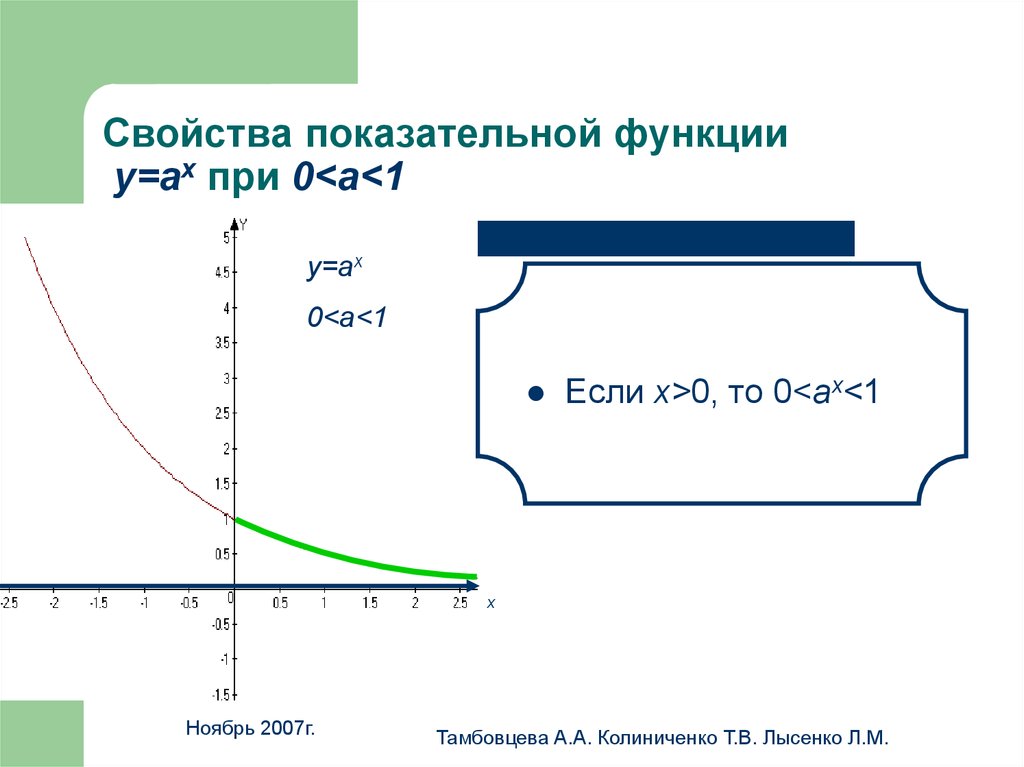
19. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
Если х>0, то 0<аx<1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
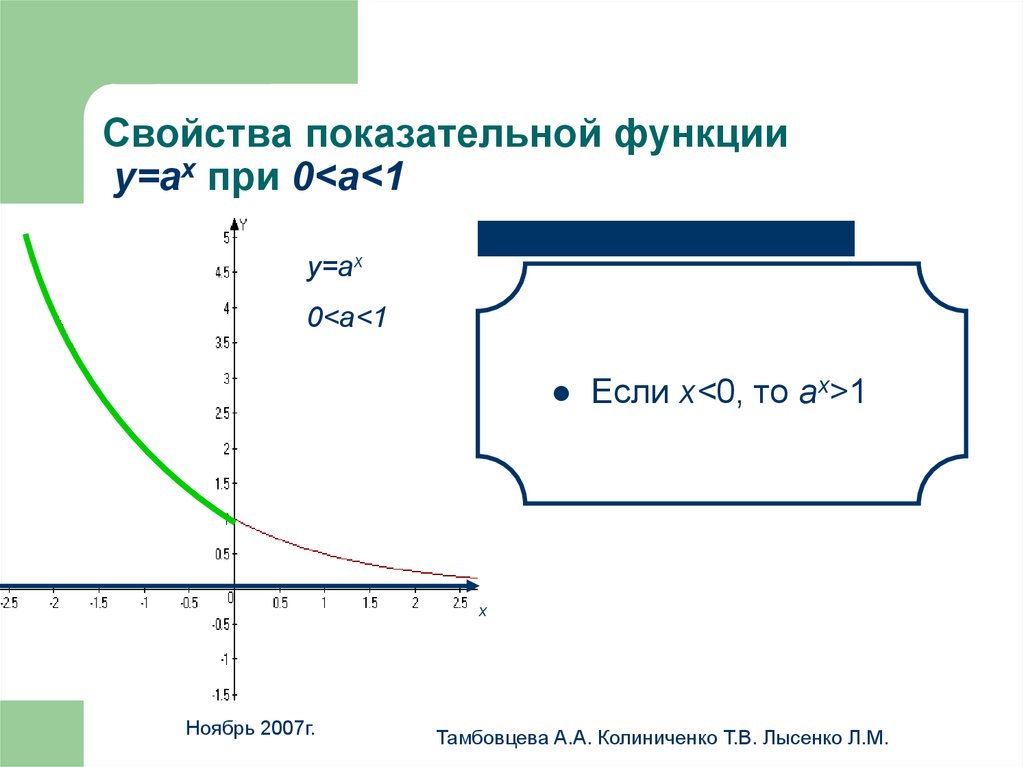
20. Свойства показательной функции у=аx при 0<a<1
Свойства показательной функцииу=аx при 0<a<1
у=аx
0<a<1
Если х<0, то аx>1
х
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
21. Показательные уравнения
aa bbxx
Если
Если
b a ,
то
b 0,
m
a a
x
m
и
x m
Ноябрь 2007г.
Если
b 0,
то
то
a b
a b
x
x log a b
x
не
имеет
корней
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
22. Показательные неравенства
a b;x
a b;
a b;
x
x
0 a 1
Если
a x гдеb,
a b.
x
1.
где b am a x am x m
1. x
m
a
b
,
b
a
, b 0 x log a b
2. x
3. a x b , если b 0 , то не имеет решения
4. a b, если b 0 , то x R
a 1
b a m x m
Если
1. a x b, где
x
a
2. b , где b a ,
m
Ноябрь 2007г.
b 0 x log a b
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
23. Производная и первообразная
ax
a ln a
x
ax
F x
C
ln a
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
24. Тест 1
Кликните по ссылке для открытия теста 1Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
25. Тест 2 Проверь себя !
1.2.
3.
4.
5.
6.
7.
«-»
«-»
«+»
«-»
«+»
«-»
«+»
8. «-»
15. «+»
9. «+»
16. «-»
10. «-»
17. «+»
11. «+»
18. «-»
12. «+»
19. «-»
13. «+»
20. «-»
14. «+»
21. «+»
18-21 правильных ответов – «5», 14-17 – «4», 11-13 – «3»,
меньше 11 – не владеете материалом
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
26. Основные опорные сигналы
1.А 0
В 0
А В 0
А В А В
6.
А, В
2.
А
0
В
3. А 0
4.
5.
9.
А 0
В 0
A 0
A 0
А2 В 2 0
А 0
A 0
A 0
A 0
B 0
A 0
А 1 B 0
Ноябрь 2007г.
В 0
А В2
8.
или
и
А 0
А В
А2 В А В
В
А В
7.
B 0
2
A B
A 0
B 0
А А
В С
А 0
В С
или
В 0, С 0
A 1
В
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
А 0
B C 0
27. Способы решения уравнений
Разложение левой части на множители.Замена переменной.
Функциональный (с помощью свойств
функции).
Однородные (делением обеих частей на
выражение не равное нулю)
Графический.
Логарифмирование.
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
28. Проверь себя! Тест 3, часть 1
1. Опора 9 , функциональный способ2. Опора 1 , функциональный способ
3. Опора 8 , замена переменной, функциональный способ
4. Опора 3 , функциональный способ, метод интервалов
5. Опора 6 , однородные уравнения
6. Опора 2 , замена переменной, разложение на множители
7.
замена переменной, метод интервалов
8. Опора 7 , функциональный способ
9. Опора 2 , замена переменной, функциональный способ
10. Опора 5 , a a, если a 0
a, если а 0
11. Опора 1
12.
13. Опора 5
14. Опора 4
15.
-
, функциональный способ
, графический способ
, геометрическая прогрессия
, функциональный способ
, замена переменной, метод интервалов1
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
29. Указания к заданиям 16 - 19
16. Используйте основное свойство дроби и исследование решенийлинейного уравнения.
1
17. 2 3
2 3
18. Базовые знания – производная и первообразная показательной функции.
19. Записать данную функцию в виде степени с основанием 2. опереться на
свойства показательной и квадратичной функций.
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
30. Решите. Тест 3 (часть2)
Вариант 1.Решите уравнение, в ответ запишите наименьший корень
х
sin x
5 x 2 4 x
1
Вариант 2.
Решите уравнение, в ответ запишите корень или сумму корней
3
Вариант 3.
Решите уравнение
Ноябрь 2007г.
x
81 3
2
x 2 3 x 2
9 lg 4 3 x 0
x
2
4 5
x 2 x 6
2
1 0
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
31. Проверь себя!
Вариант 1Решите уравнение. В ответ запишите наименьший корень х
Решение.
х 1
х
sin x
5 x 2 4 x
Ответ: -
1
2
х 4 х 5 0
x 0
x 1
sin x
5 x 2 4 x
х 1
2
х 4 х 5 0
x 0
x 1
sin x 0
x 2 4 x 5 0
sin x
5 x 2 4 x
x 1
5 x 1
x 0
x 1
x n, n Z
5 x 1
1.
х 1
x
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
32. Проверь себя!
3Решите
уравнение.
Решение. Так как
3
x
81 3
x
x
Вариант 2
x
3 x 81 0
9 lg 4 3 x
81 3 9 lg 4 3 x 0.
при любых х, то
x
3 9 0
x
4 3 0
0
x
4 3 1
x
3 9 0
x 2
x 2
x 2
3 x 4
x 2
x
3 3
x
2
3 3
Ответ: -2
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.
33. Проверь себя!
Решите уравнение.Решите уравнение.
Решение. 2
х 2 3 х 2
2
4 5
2
Вариант 3
х 2 3 х 2
х 2 х 6
2
4 5х
2
х 6
2
1 0.
х 3 х 2
х 3 х 2
2
4 0
22
2
2
х 3х 0
1 0 2
2
2
х х 6
х х 6
0
х
х
6
5
1
0
5
5
2
2
2
х 0
х 3
х 3
х
2
х 3
Ответ: 3
Ноябрь 2007г.
Тамбовцева А.А. Колиниченко Т.В. Лысенко Л.М.




















 mathematics
mathematics








