Similar presentations:
Решение уравнений, сводящихся к квадратным
1.
Цель урока: Закрепление навыков решенияквадратных уравнений. Формирование у
учащихся умения решать биквадратные
уравнения .
2.
• X2=9• X2=71
• X2=64
• x2=7
X2=
49
81
3.
Биквадратное уравнениеax bx c 0
4
Обозначим
2
x2=t ,t ≥ 0
at bt c 0
2
4.
Алгоритм решения квадратногоуравнения
• Выписать коэффициенты квадратного уравнения
at2+bt+c=0
• Найдем D по формуле D=b2-4ac
при D>0 уравнение имеет
2 корня
при D=0 уравнение имеет
1 корень
при D<0 уравнение не имеет действительных
корней
• Записываем ответ
5. Алгоритм решения квадратного уравнения
Рассмотрим решение биквадратногоуравнения вида
x x c 0
4
x
2
4
x c
2
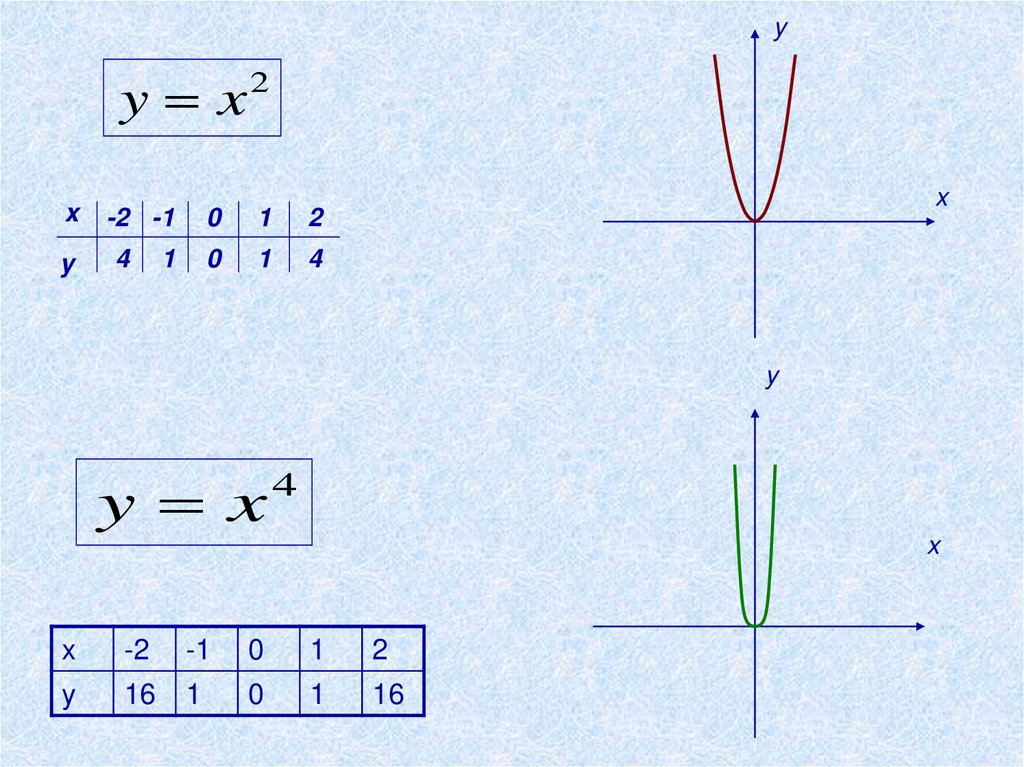
Построим графики функций
y x
4
y x c
2
6.
yy x
x
y
-2 -1
4
1
2
0
1
2
0
1
4
x
y
y x
4
x
x
-2
-1
0
1
2
y
16
1
0
1
16
7.
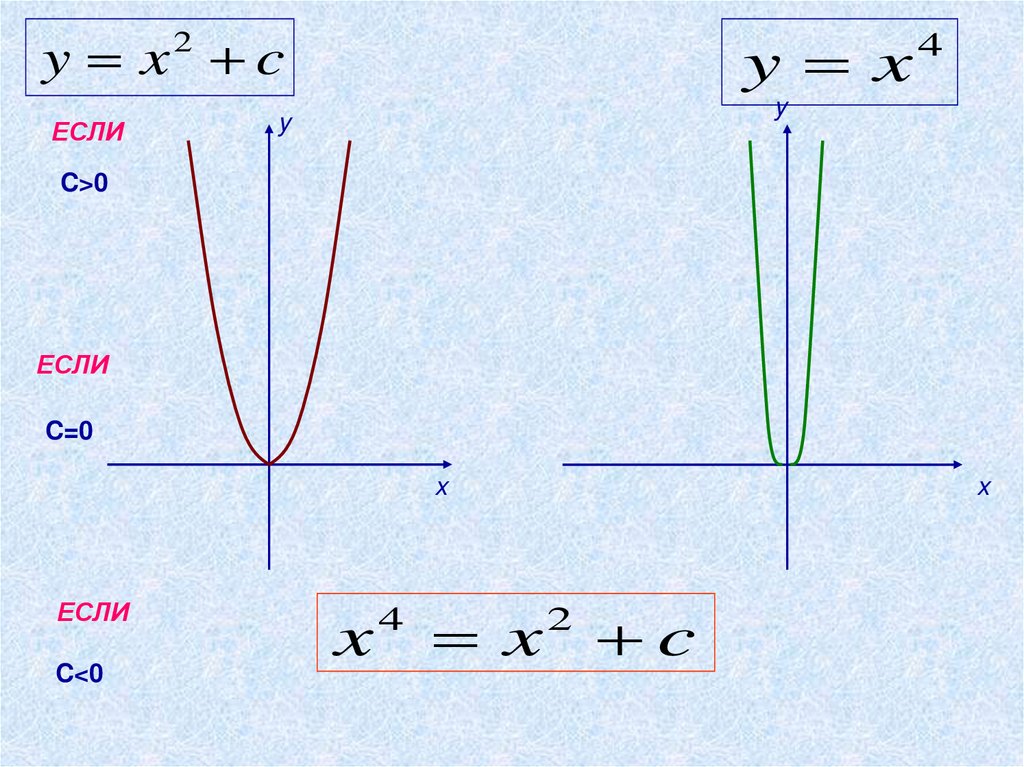
y x cy x
2
ЕСЛИ
4
y
y
C>0
ЕСЛИ
C=0
x
ЕСЛИ
C<0
x
4
x
x c
2
8.
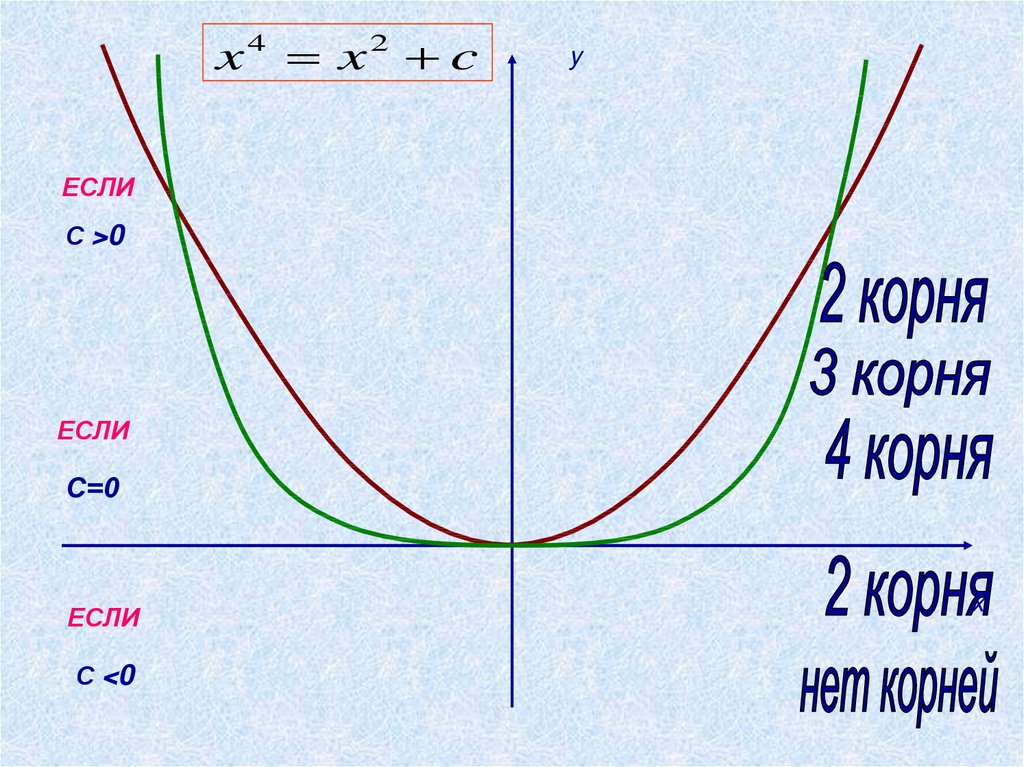
Сколько корней имеетбиквадратное
уравнение?
9.
x4 x2 cy
ЕСЛИ
С >0
ЕСЛИ
С=0
ЕСЛИ
С <0
x
10. Сколько корней имеет биквадратное уравнение?
Биквадратное уравнениеax bx c 0
4
2
Обозначим
x2=t ≥ 0
at bt c 0
2
11.
Алгоритм решениябиквадратного уравнения
ax 4 bx 2 c 0
Вводим новую переменную x2=t ,t ≥ 0
Составляем квадратное уравнение относительно t
Решаем квадратное уравнение
Выбираем корни удовлетворяющие условию t ≥ 0
Решаем неполное квадратное уравнение
Записываем ответ
at 2 bt c 0
12.
2 x 3x 5 04
Обозначим
2
x2=t ,t ≥ 0
2t 3t 5 0
2
13. Алгоритм решения биквадратного уравнения
2t 3t 5 02
а 2, b 3, c 5
D b 2 4ac
D 32 4 2 ( 5) 9 40 49 0
t1
3 49
3 7
1
2 2
4
3 49
3 7 10
t2
2,5
2 2
4
4
Не уд. усл.
t 0
x2 1
x1 1, x2 1
Ответ:
x1 1, x2 1
14.
Самостоятельная работа2 x 5x 3 0
4
2
5 x 3x 2 0
4
2


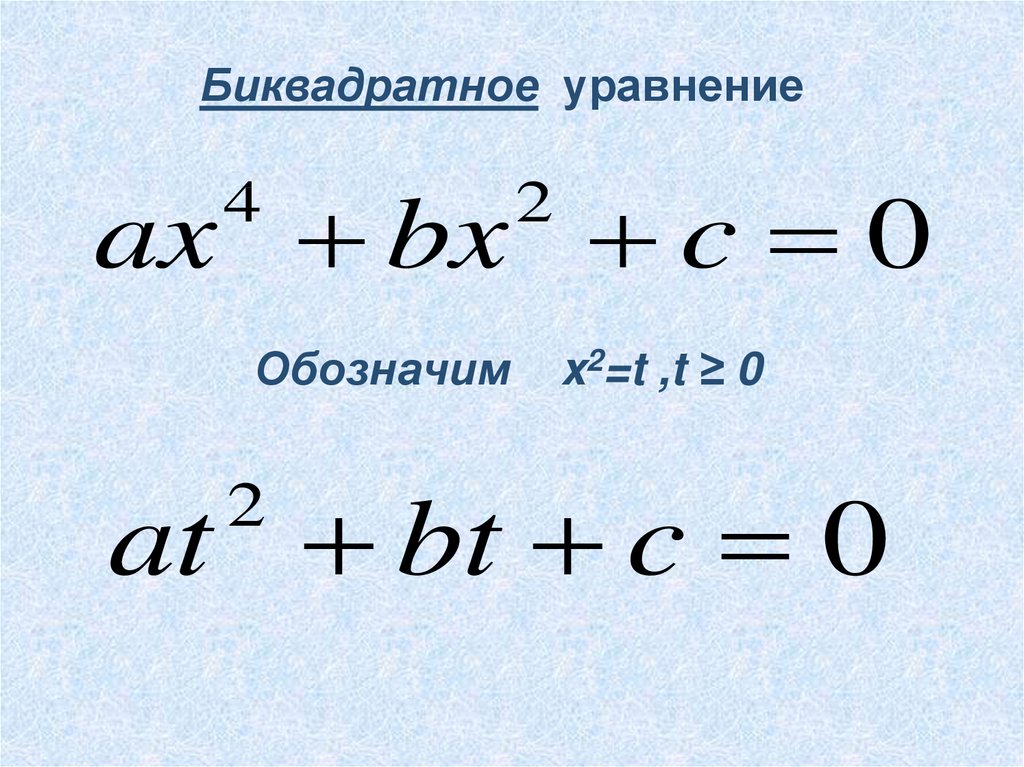



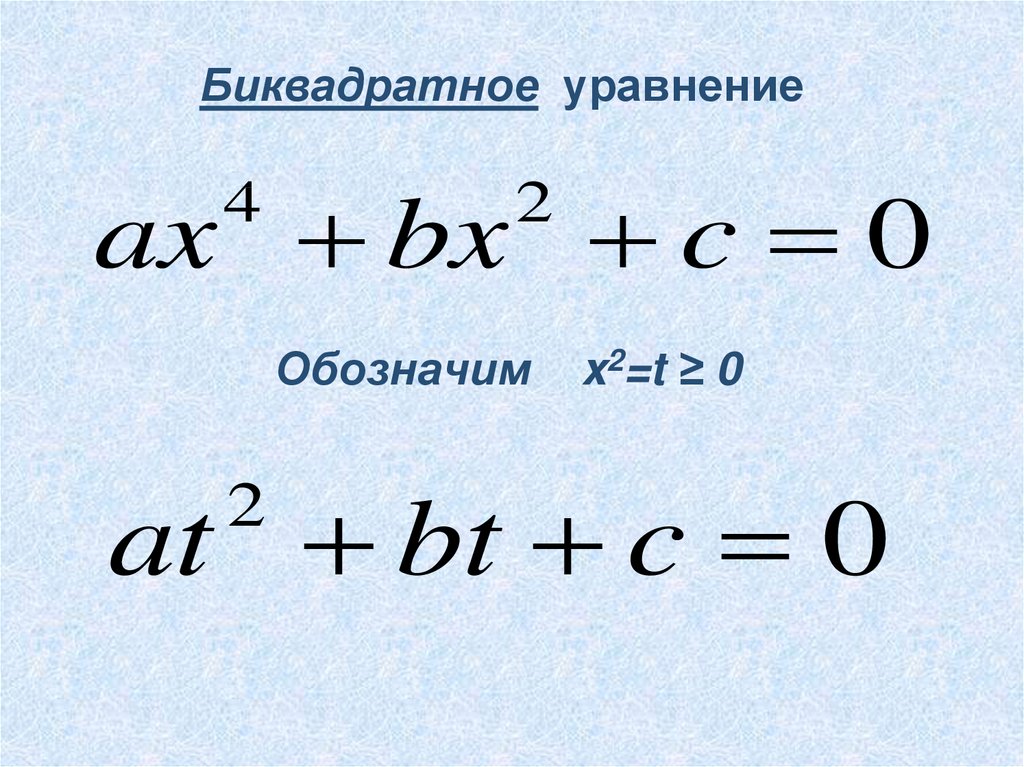




 mathematics
mathematics








