Similar presentations:
Кинематика. Раздел теоретической механики, в котором изучается движение
1.
КИНЕМАТИКАКИНЕМАТИКА
2.
КинематикаКинематика
Кинематика – это раздел теоретической механики, в котором изучается движение точек и тел без учета их
масс и действующих на них сил.
Основные задачи кинематики:
• Задать закон движения тела.
• По этому закону найти основные кинематические характеристики (траекторию, скорость, ускорение).
3. Способы задания движения точки
КинематикаКинематика точки
точки
Способы задания движения точки
• 1) Векторный.
• 2) Координатный.
• 3) Естественный.
4. Векторный способ задания движения точки
КинематикаКинематика точки
точки
Векторный способ задания движения
точки
М
r
О
r = r(t)
5.
КинематикаКинематика точки
точки
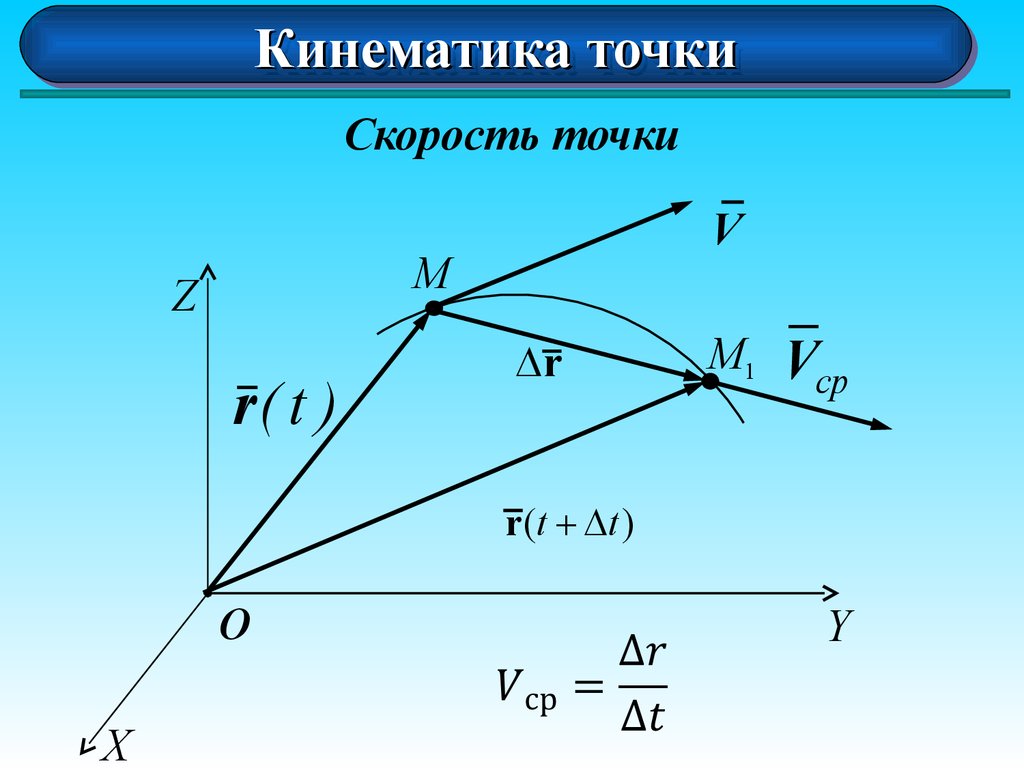
Скорость точки
V
M
Z
r( t )
Dr
M1
Vср
r (t + Dt )
o
X
Y
6.
КинематикаКинематика точки
точки
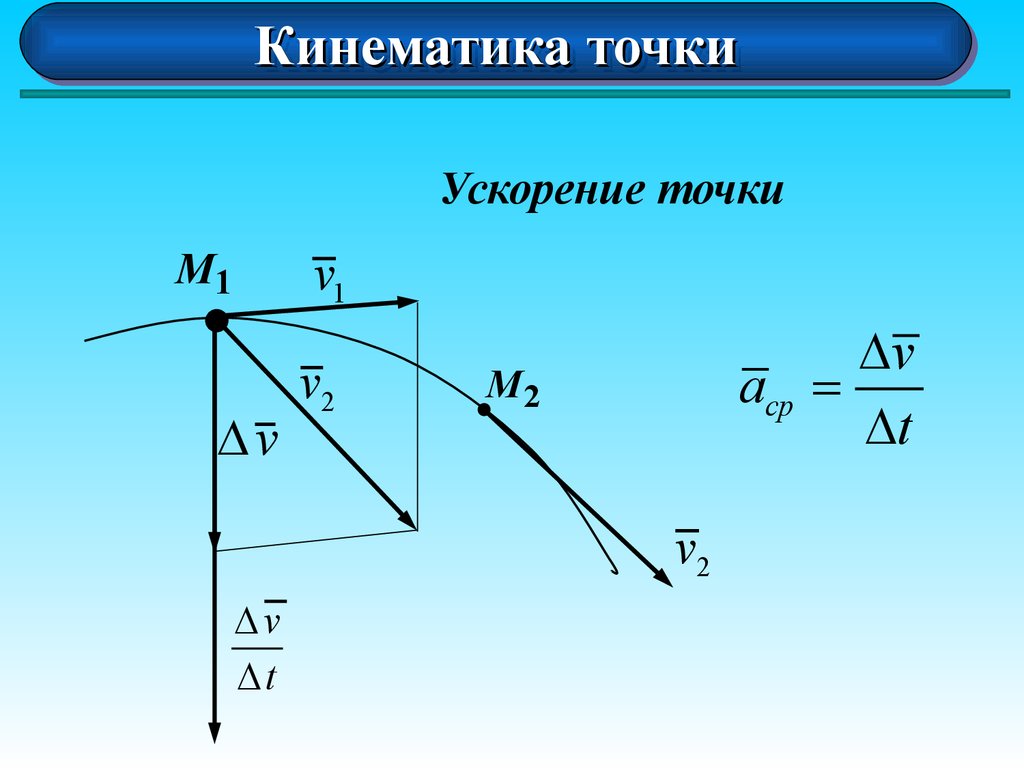
Ускорение точки
M1
v1
Dv
v2
Dv
acp =
Dt
M2
v2
Dv
Dt
7.
КинематикаКинематика точки
точки
Координатный способ задания движения точки
z
x = x(t );
М
z
О
x
y
x
y
y = y (t );
z = z (t ).
8.
КинематикаКинематика точки
точки
Связь между координатным и
векторным способами
z
r (t ) = x(t )i + y (t ) j + z (t )k
r
k
i
x
j
y
M
z
x
y
9.
КинематикаКинематика точки
точки
Скорость точки при координатном способе задания движения
dr dx
dy
dz
V =
= i+
j+ k
dt dt
dt
dt
dx
Vx =
dt
dy
Vy =
dt
dz
Vz =
dt
10.
КинематикаКинематика точки
точки
Другая форма записи:
Vx = x&; Vy = y&; Vz = z&;
(Точка означает производную по времени)
Проекции скорости на оси координат равны
первым производным от соответствующих
координат по времени
Модуль скорости и угол между вектором и
координатными осями:
V = x& + y& + z& ;
2
2
2
x&
cos( i V ) = .
V
Ù
11.
КинематикаКинематика точки
точки
Ускорение точки
2
dV d r
a=
= 2
dt
dt
& j + V&k = &
&+ &
&.
a = V&
i
+
V
xi
y&j + &
zk
x
y
z
&= &
&= &
&
&
&
ax = V&
=
x
;
a
=
V
y
;
a
=
V
z&
;
x
y
y
z
z
a= &
x& + &
y& + &
z&;
2
2
2
&
x&
cos( i a ) = .
a
Ù
12.
КинематикаКинематика точки
точки
Проекции ускорения на оси координат равны
первым производным от проекций скорости или
вторым
производным
соответствующих
координат точки по времени
13.
КинематикаКинематика точки
точки
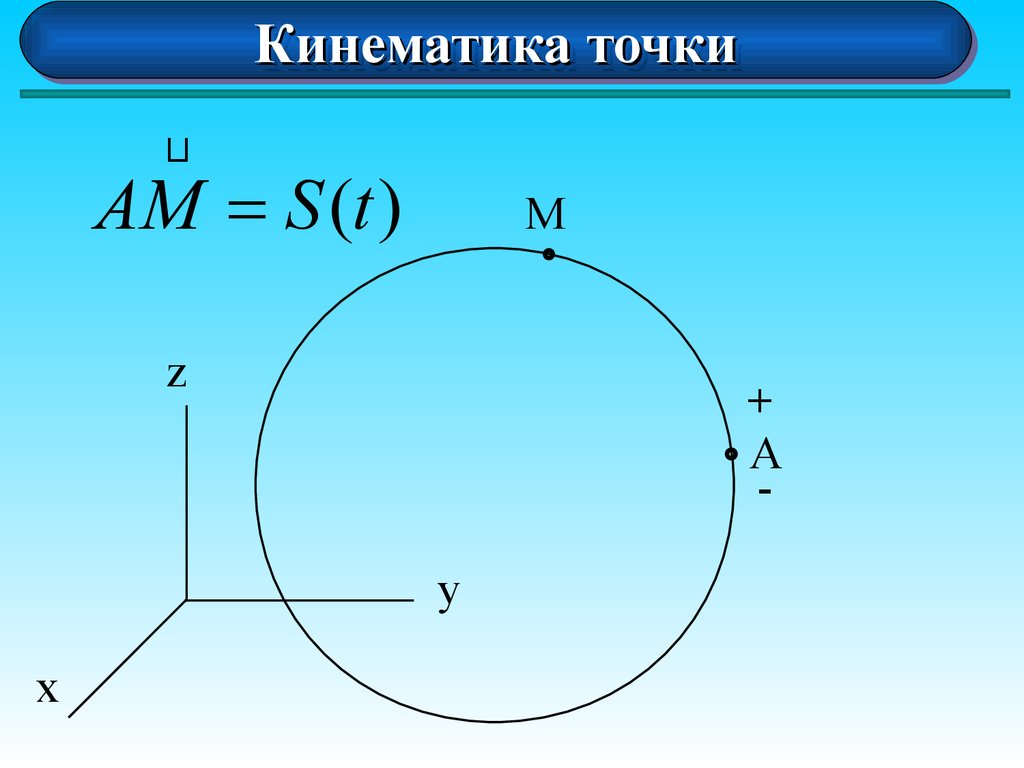
Естественный способ задания движения точки
Задается:
• траектория движения;
• начало и положительное направление
отсчета;
• закон движения точки по траектории:
S=S(t).
14.
КинематикаКинематика точки
точки
AM = S (t )
M
z
+
A
y
x
15.
КинематикаКинематика точки
точки
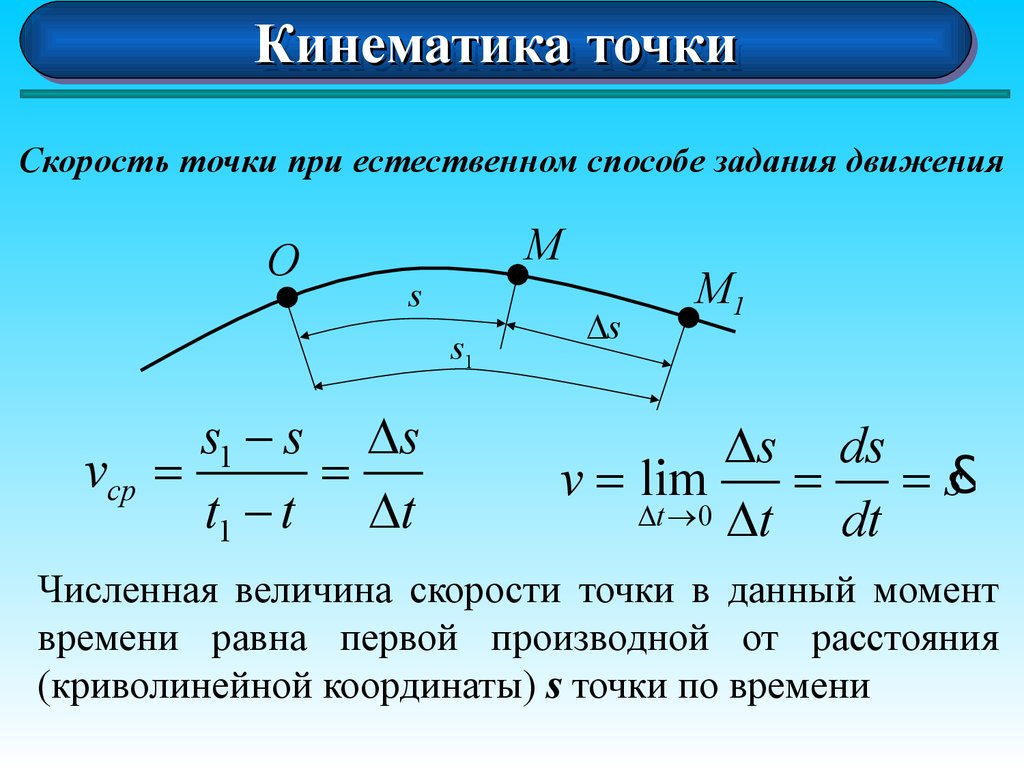
Скорость точки при естественном способе задания движения
O
M
s
s1
s1 - s Ds
vcp =
=
t1 - t Dt
Ds
M1
Ds ds
v = lim
=
= s&
Dt ® 0 Dt
dt
Численная величина скорости точки в данный момент
времени равна первой производной от расстояния
(криволинейной координаты) s точки по времени
16.
КинематикаКинематика точки
точки
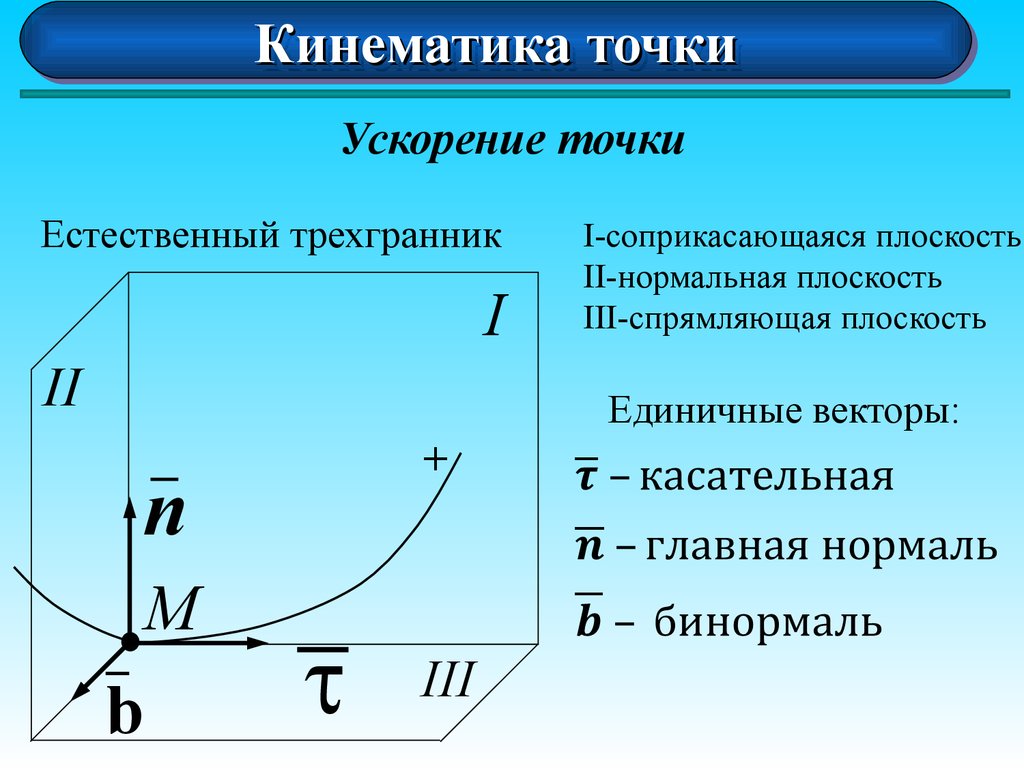
Ускорение точки
Естественный трехгранник
I
II
I-соприкасающаяся плоскость
II-нормальная плоскость
III-спрямляющая плоскость
Единичные векторы:
+
n
M
b
t
III
17.
КинематикаКинематика точки
точки
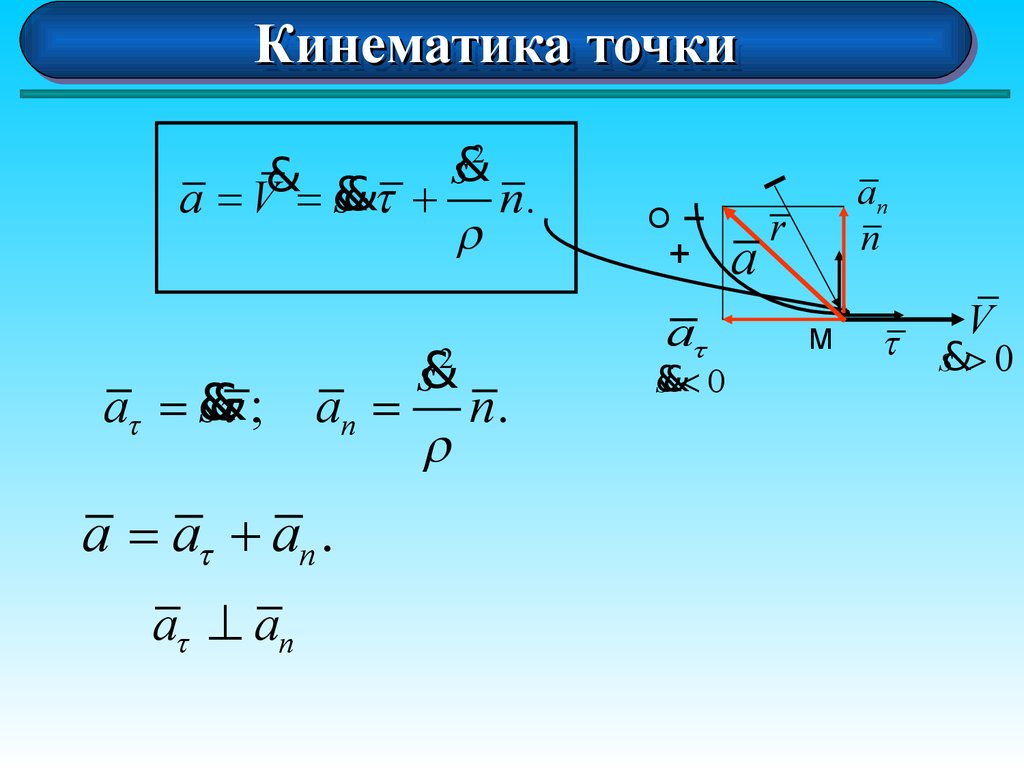
2
&
s
&
a =V = &
s&×t + n .
r
at = &
s&
t;
s&
an = n .
r
a = at + an .
at ^ an
2
О
+
at
&
s&< 0
a
an
n
r
М
t
V
s&> 0
18.
КинематикаКинематика точки
точки
Проекция ускорения точки на касательную равна
первой производной от численной величины скорости
или второй производной от расстояния (криволинейной
координаты) s точки по времени, а проекция ускорения
на главную нормаль равна квадрату скорости,
деленному на радиус кривизны треактории в данной
точке кривой
19.
КинематикаКинематика точки
точки
При координатном задании движения могут быть
использованы также цилиндрические и сферические
координаты, а при движении точки в плоскости –
полярные.
20. Цилиндрическая система координат
КинематикаКинематика точки
точки
Цилиндрическая система координат
z
Закон движения:
r = r t ,
= t ,
z = z t.
.
M
z
O
x
r
y
Формулы перехода к декартовым координатам:
x = r cos f ,
y = r sin f ,
z = z.
21. Сферическая система координат
КинематикаКинематика точки
точки
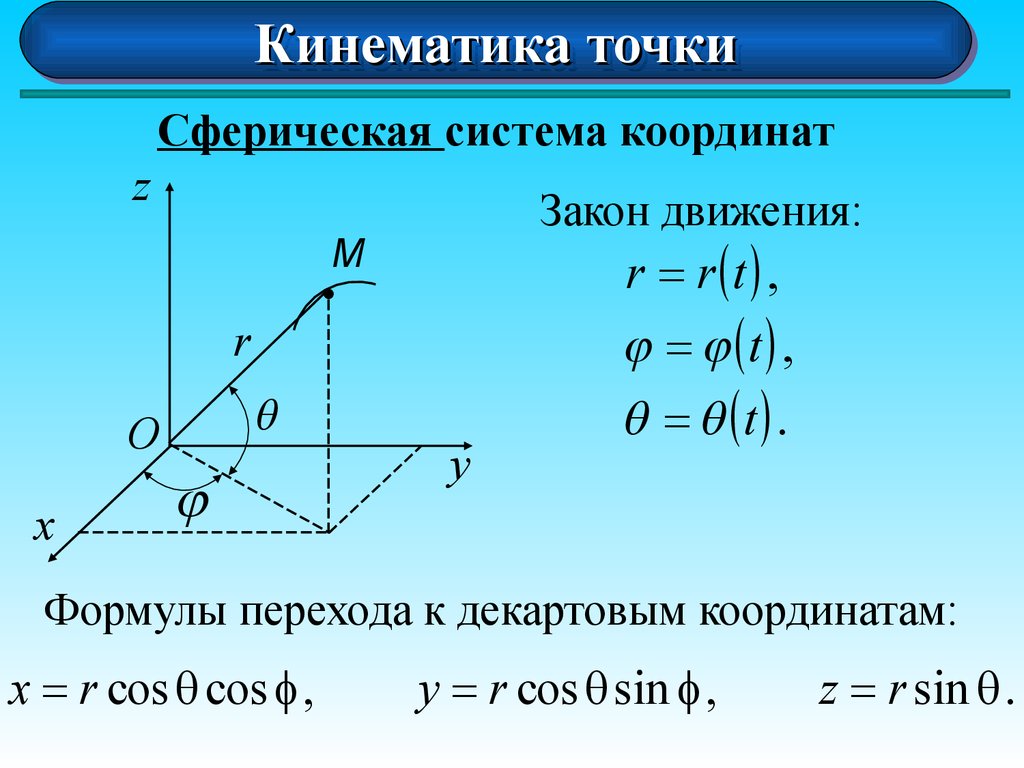
Сферическая система координат
z
Закон движения:
.
M
r
O
x
y
r = r t ,
= t ,
= t .
Формулы перехода к декартовым координатам:
x = r cos cos f ,
y = r cos sin f ,
z = r sin .
22. Полярные координаты
КинематикаКинематика точки
точки
Полярные координаты
Их иногда используют при движении точки в
плоскости.
Закон движения:
y
М
.
r
O
r = r t ,
= t .
x
Формулы перехода к декартовым координатам:
x = r cos f ,
y = r sin f .














 mechanics
mechanics








